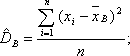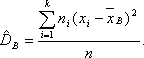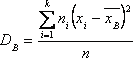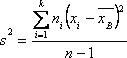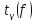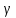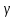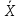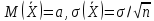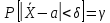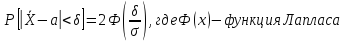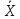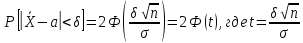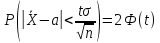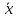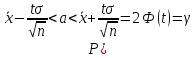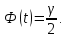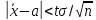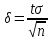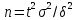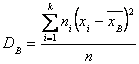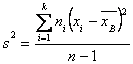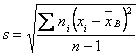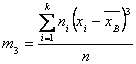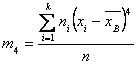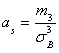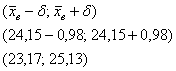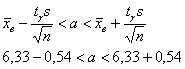Как найти несмещенные оценки генеральной дисперсии - Исправление недочетов и поиск решений вместе с Examum.ru

Несмещенная оценка выборочной дисперсии

Краткая теория

Пусть из генеральной совокупности в результате

независимых наблюдений над количественным
признаком

извлечена повторная выборка объема

При этом

Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию

.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой

,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:

Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить

на дробь

.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через

Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:

Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:

Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:

При достаточно больших значениях

объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно

Пример решения задачи

Задача

Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.

Сумма
частот:

Вычислим
среднюю:

Средняя квадратов:

Несмещенная
выборочная дисперсия:

Ответ:

Кроме этой задачи на другой странице сайта есть

пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда

Источник

Для
того, чтобы наблюдать рассеяние
количественного признака значений
выборки вокруг своего среднего значения
, вводят сводную характеристику-
выборочную дисперсию.

Выборочной
дисперсией называют
среднее арифметическое квадратов
отклонения наблюдаемых значений
признака от их среднего значения .

Если
все значения признака выборки различны,
то

если
же все значения имеют частоты n₁, n₂,…,n_k,
то

Для
характеристики рассеивания значений
признака выборки вокруг своего среднего
значения пользуются сводной характеристикой
— средним квадратическим отклонением.

Вычисление
дисперсии- выборочной или генеральной,
можно упростить, используя формулу:

Замечание:
если выборка представлена интервальным
вариационным рядом, то за x_i принимают
середины частичных интервалов.

Для
исправления выборочной дисперсии
достаточно умножить ее на дробь

получим исправленную
дисперсию S².
Исправленная дисперсия является
несмещенной оценкой.

В
качестве оценки генеральной дисперсии
принимают исправленную дисперсию.

Для
оценки среднего квадратического
генеральной совокупности
используют исправленное
среднее квадратическое отклонение

Пример:
По
выборке объема N=41 найдена
смещенная оценка генеральной дисперсии .
Найти несмещенную оценку дисперсии
генеральной совокупности.

Решение. Смещенной
оценкой генеральной дисперсии служит
выборочная дисперсия

Несмещенной
оценкой генеральной дисперсии является
«исправленная дисперсия»

или

Таким
образом, мы получаем искомую несмещенную
оценку дисперсии генеральной совокупности:

11. Интервальные
оценки неизвестных параметров генеральной
совокупности. Доверительная вероятность.
Интервальная оценка мат. ожидания
нормально распределенного признака
при известном среднем квадратическом
отклонении.

Интервальной оценкой
называется числовой интервал, который
определяется двумя числами – границами
интервала, содержащего неизвестный
параметр генеральной совокупности.

Доверительным
интервалом называется интервал, в
котором с той или иной заранее заданной
вероятностью находится неизвестный
параметр генеральной совокупности.

Доверительная
вероятность –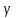
вероятность, что событие вероятности 1-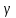 можно
считать невозможным, a
= 1- –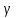
уровень значимости. В качестве
доверительных вероятностей используют
вероятности, близкие к 1 (например, 0,95;
0,99; 0,999).

Для
малых выборок (n<30) нормально
распределенного количественного
признака Х доверительный интервал имеет
вид:

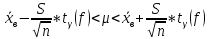
где
– коэффициент
Стьюдента, значение которого определяется
величиной доверительной вероятности
и числом степеней свободы f
= n
— 1.

Для
больших выборок (n<30) нормально
распределенного количественного
признака Х доверительный интервал имеет
вид:

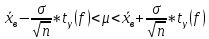
где –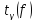
коэффициент Стьюдента, значение которого
определяется величиной доверительной
вероятности
и числом степеней свободы
f
= n
– 1.

Пусть
математическое ожидание выборочной
средней

нормального распределения равно a и
среднее квадратическое отклонение –
σ.

Требуется
найти доверительные интервалы, покрывающие
параметр a
с надежностью γ, т.е.

Для
решения воспользуемся формулой вычисления
вероятности заданного отклонения из
теории вероятностей:

Проведя
замены X на

и σ на
,
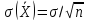
получим

Найдя
из последнего равенства
,
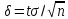
можем написать

Приняв
во внимание, что доверительная вероятность
задана и равна γ, и заменив выборочную
среднюю на

окончательно
имеем

Смысл
полученного равенства:

С
надежностью γ можно утверждать, что
доверительный интервал
)
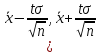
покрывает неизвестный параметр a,
точность оценки
.

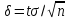
Число
t определяется из соотношения
.

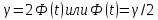
По
таблице функции Лапласа находят аргумент
t, которому соответствует значение
функции Лапласа

Замечание
1. Оценку

называют классической. Из формулы
точности оценки

следуют выводы:

1)
При возрастании объема выборки n число
δ убывает, следовательно точность
увеличивается;

2)
Увеличение надежности оценки приводит
к увеличению t. Как следствие, возрастает
δ и уменьшается точность оценки.

Замечание
2. Как следует из равенства точности
оценки, минимальный объем выборки,
который обеспечит заданную точность
оценки математического ожидания, равен:

Источник

Задача 55. Из генеральной совокупности извлечена выборка объема N, заданная вариантами ХI и соответствующими им частотами. Найти несмещенную оценку генеральной средней.

Варианта ХI	2	5	7	10
Частота Ni	16	12	8	14

Решение. Множество всех объектов, подлежащих изучению, называется Генеральной совокупностью. Множество случайно отобранных объектов называется выборочной совокупностью или Выборкой.

Для оценки неизвестных параметров теоретического распределения служат статистические оценки. Статистическая оценка, определяемая одним числом, называется Точечной оценкой.

Точечная статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется Несмещенной оценкой. Статистическая оценка, математическое ожидание которой не равно оцениваемому параметру является Смещенной.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя

(1),

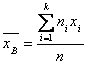
Где ХI – варианта выборки (элемент выборки); Ni – частота варианты ХI (число наблюдений варианты ХI); – объем выборки (число элементов совокупности).

Объем данной выборки равен .

Далее по формуле (1) вычисляем несмещенную оценку генеральной средней:

Задача 56. По выборке объема N=41 найдена смещенная оценка генеральной дисперсии . Найти несмещенную оценку дисперсии генеральной совокупности.

Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия

Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»

или

Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности:

Задача 57. Найти доверительный интервал для оценки с надежностью P=0,95 неизвестного математического ожидания A нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение S=5, выборочная средняя , а объем выборки N=25.

Решение. Интервальной оценкой называется интервал, покрывающий оцениваемый параметр. Доверительным интервалом является интервал, который с данной надежностью покрывает оцениваемый параметр.

Для оценки математического ожидания A нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал

Где – точность оценки, T – значение аргумента функции Лапласа (приложение, таблица 2).

В данной задаче T находим из условия . По таблице 2 определяем . Таким образом, T=1,96.

Далее получаем

Или

Задача 58. По данным N=9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью =0,99.

Решение. Оценкой математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения является доверительный интервал

По таблице 3 приложения, по заданным N и находим =3,36.

Таким образом

Окончательно получаем

Задача 59. Из генеральной совокупности извлечена выборка объема N. Оценить с надежностью =0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.

Значение признака ХI	-2	1	1	3	4	5
Частота Ni	2	1	2	2	2	1

Решение. Объем данной выборки равен

По данным задачи находим выборочную среднюю:

Далее находим исправленное среднее квадратическое отклонение S:

Для оценки математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения служит доверительный интервал

По таблице 3 приложения по заданным N и находим =2,26.

Таким образом

Окончательно получаем

Задача 60. Построить полигон частот и эмпирическую функцию по данному распределению выборки:

Варианты ХI	-3	0	1	4	6	7
Частоты Ni	3	6	1	2	5	1

Решение. Полигоном частот называют ломаную, отрезки которой соединяют точки ; ;…;, где ХI – варианты выборки, Ni – соответствующие им частоты.

Полигон частот для данного распределения изображен на рисунке 15.

Рис. 15

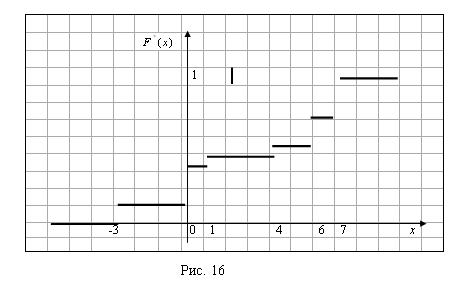
Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения X относительную частоту события :

Где – число вариант, меньших Х; N – объем выборки.

Из определения следует, что .

Найдем эмпирическую функцию распределения.

Объем данной выборки равен =18.

Если , то =0 (так как -3 – наименьшая варианта). Если , то значение , а именно наблюдалось 3 раза, следовательно, . При значения , а именно и наблюдались 3+6=9 раз, следовательно, .

Аналогично получаем, что при функция распределения ; при функция распределения ; при функция распределения . Далее, если , то (так как 7 – наибольшая варианта).

Таким образом, эмпирическая функция распределения равна:

График полученной эмпирической функции распределения изображен на рисунке 16.

Задача 61. Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема N=100:

Варианта ХI	48	52	56	60	64	68	72	76	80	84
Частота Ni	2	4	6	8	12	30	18	8	7	5

Решение. Асимметрия эмпирического распределения определяется равенством:

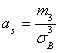
Где — центральный эмпирический момент третьего порядка, вычисляемый по формуле:

Эксцесс эмпирического распределения определяется равенством:

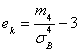
Где — центральный эмпирический момент четвертого порядка, вычисляемый по формуле:

Асимметрия и эксцесс служат для оценки отклонения эмпирического распределения от нормального. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Кроме того, если эксцесс положительный, то распределение будет островершинным; если отрицательный, то распределение будет плосковершинным по сравнению с нормальным распределением.

Для практического расчета асимметрии и эксцесса непосредственно пользоваться вышеуказанными формулами довольно затруднительно, поэтому воспользуемся методом сумм. Составим расчетную таблицу 1, для этого:

1) Запишем варианты в первый столбец.

2) Запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца.

3) В качестве ложного нуля С выберем варианту (68), которая имеет наибольшую частоту (в качестве С можно взять любую варианту, расположенную примерно в середине столбца); в клетках строки, содержащей ложный нуль, запишем нули; в четвертом столбце над и под уже помещенным нулем запишем еще по одному нулю.

4) В оставшихся незаполненными над нулем клетках третьего столбца (исключая самую верхнюю) запишем последовательно накопленные частоты:

2; 2+4=6; 6+6=12; 12+8=20; 20+12=32.

Сложив все накопленные частоты, получим число B1=72, которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты:

5; 5+7=12; 12+8=20; 20+18=38.

Сложив все накопленные частоты, получим число A1=75, которое поместим в нижнюю клетку третьего столбца.

5) Аналогично заполняется четвертый столбец, причем суммируют частоты третьего столбца. Сложив все накопленные частоты, расположенные над нулем, получим число B2=70, которое поместим в верхнюю клетку четвертого столбца. Сумма накопленных частот, расположенных под нулем, равна числу A2=59, которое поместим в нижнюю клетку четвертого столбца.

6) Для заполнения столбца 5 запишем нуль в клетке строки, содержащей ложный нуль (68); над этим нулем и под ним поставим еще по два нуля. В клетках над нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 сверху вниз; в итоге будем иметь следующие накопленные частоты:

2; 2+8=10; 10+20=30.

Сложив накопленные частоты, получим число B3=42, которое поместим в верхнюю клетку пятого столбца. В клетках под нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 снизу вниз; в итоге будем иметь следующие накопленные частоты:

5; 5+17=22.

Сложив накопленные частоты, получим число A3=27, которое поместим в нижнюю клетку пятого столбца.

7) Аналогично заполняется столбец 6, причем суммируют частоты столбца 5.

В итоге получим расчетную таблицу 1:

Расчетная таблица 1

1	2	3	4	5	6
ХI	Ni	B1=72	B2=70	B3=42	B4=14
48	2	2	2	2	2
52	4	6	8	10	12
56	6	12	20	30	0
60	8	20	40	0	0
64	12	32	0	0	0
68	30	0	0	0	0
72	18	38	0	0	0
76	8	20	37	0	0
80	7	12	17	22	0
84	5	5	5	5	5
	N=100	A1=75	A2=59	A3=27	A4=5

Теперь найдем Di (I=1, 2, 3) и si (I=1, 2, 3, 4):

; ; ;

; ;

; .

Найдем условные моменты первого, второго, третьего и четвертого порядков:

; ;

;

Найдем далее центральные эмпирические моменты третьего и четвертого порядков, учитывая, что шаг (разность между двумя соседними вариантами):

;

Так как дисперсия , то выборочное среднее квадратическое отклонение .

Учитывая определения асимметрии и эксцесса, окончательно получаем:

; .

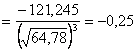
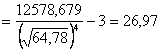
< Предыдущая		Следующая >

Источник

Статистические оценки параметров генеральной совокупности

Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Интервальные статистические оценки. Точность и надежность оценки; определение доверительного интервала; построение доверительных интервалов для средней при известном и неизвестном среднеквадратическом отклонении.

Определение статистической оценки

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности по нормальному закону, то необходимо оценить математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Если имеются основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр lambda , которым это распределение определяется. Обычно имеются лишь данные выборки, полученные в результате наблюдений: x_1,x_2,ldots,x_n . Через эти данные и выражают оцениваемый параметр. Рассматривая как значения независимых случайных величин можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения означает найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

Точечные статистические оценки

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные.

Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть Theta^* есть статистическая оценка неизвестного параметра Theta теоретического распределения. Допустим, что по выборке объема найдена оценка Theta_1^* . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку Theta_2^* и т. д. Получим числа Theta_1^*,Theta_2^*,ldots,Theta_k^* , которые будут различаться. Таким образом, оценку Theta^* можно рассматривать как случайную величину, а числа — как возможные ее значения.

Если оценка Theta^* дает приближенное значение Theta с избытком, то найденное по данным выборок число Theta~(k=1,2,ldots,n) будет больше истинного значения Theta . Следовательно, и математическое ожидание (среднее значение) случайной величины Theta^* будет превышать Theta , то есть M(Theta^*)>Theta . Если Theta дает приближенное значение Theta с недостатком, то M(Theta^*)<Theta .

Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки Theta было равно оцениваемому параметру. Соблюдение требования M(Theta^*)=Theta устраняет систематические ошибки.

Несмещенной называют статистическую оценку Theta^* , математическое ожидание которой равно оцениваемому параметру Theta , то есть M(Theta^*)=Theta .

Смещенной называют статистическую оценку Theta^* , математическое ожидание которой не равно оцениваемому параметру.

Однако ошибочно считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения Theta^* могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия величины Theta^* может быть значительной. В этом случае найденная по данным одной выборки оценка, например Theta^* , может оказаться удаленной от своего среднего значения $overline{Theta^*}$ , а значит, и от самого оцениваемого параметра Theta . Приняв Theta_1^* в качестве приближенного значения Theta , мы допустили бы ошибку. Если потребовать, чтобы дисперсия величины Theta^* была малой, то возможность допустить ошибку будет исключена. Поэтому к статистической оценке предъявляются требования эффективности.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при ntoinfty стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при стремится к нулю, то такая оценка оказывается также состоятельной.

Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают генеральную среднюю и дисперсию.

Пусть изучается дискретная генеральная совокупность относительно количественного признака. Генеральной средней называется среднее арифметическое значений признака генеральной совокупности. Она вычисляется по формуле

$overline{x}_text{g}=frac{1}{N}sumlimits_{i=1}^{N}x_i$ или $overline{x}_text{g}=frac{1}{N}sumlimits_{i=1}^{k}x_im_i$

где x_i — значения признака генеральной совокупности объема ; m_i — соответствующие частоты, причем

$sumlimits_{i=1}^{k}m_i=N.$

Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема со значениями признака x_1,x_2,ldots,x_n . Выборочной средней называется среднее арифметическое значений признака выборочной совокупности и вычисляется по формуле

$overline{x}_text{v}=frac{1}{n}sumlimits_{i=1}^{n}x_i$ или $overline{x}_text{v}=frac{1}{n}sumlimits_{i=1}^{k}x_im_i$

где x_i — значения, признака в выборочной совокупности объема ; m_i — соответствующие частоты, причем

$sumlimits_{i=1}^{k}m_i=n.$

Если генеральная средняя неизвестна и требуется оценить ее по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещенной и состоятельной оценкой. Отсюда следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.

Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит- от объема выборки: чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной.

Для того чтобы охарактеризовать рассеяние значений количественного признака генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию. Генеральной дисперсией $D_text{g}$ называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения $overline{x}_text{g}$ , которое вычисляется по формуле

$D_text{g}=frac{1}{N}sumlimits_{i=1}^{N}(x_i-overline{x}_text{g})^2$ или $D_text{g}=frac{1}{N}sumlimits_{i=1}^{k}(x_i-overline{x}_text{g})^2m_i$

Для того чтобы охарактеризовать рассеяние наблюденных значений количественного признака выборки вокруг своего среднего значения хв, вводят сводную характеристику — выборочную дисперсию. Выборочной дисперсией $D_text{v}$ называется среднее арифметическое квадратов отклонений наблюденных значений признака от их среднего значения $overline{x}_text{v}$ , которое вычисляется по формуле

$D_text{v}=frac{1}{n}sumlimits_{i=1}^{n}(x_i-overline{x}_text{v})^2$ или $D_text{v}=frac{1}{n}sumlimits_{i=1}^{k}(x_i-overline{x}_text{v})^2m_i$

Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение. Генеральным средним квадратическим отклонением называют квадратный корень из генеральной дисперсии: $sigma_text{g}=sqrt{D_text{g}}$ . Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии: $sigma_text{v}=sqrt{D_text{v}}$ .

Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема . Требуется по данным выборки оценить неизвестную генеральную дисперсию $D_text{g}$ . Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка приведет к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой $D_text{g}$ . Другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно $M(D_text{v})=frac{n-1}{n}D_text{g}$ .

Легко исправить выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Для этого нужно умножить $D_text{v}$ на дробь $frac{n}{n-1}$ . В результате получим исправленную дисперсию s^2 , которая будет несмещенной оценкой генеральной дисперсии:

$s^2=frac{1}{n-1}sumlimits_{i=1}^{k}(x_i-overline{x}_text{v})^2m_i$

Интервальные оценки

Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.

Доверительным интервалом $Bigl(tilde{Theta}_n^{(1)};tilde{Theta}_n^{(2)}Bigl)$ для параметра Theta называется такой интервал, относительно которого с заранее выбранной вероятностью p=1-alpha , близкой к единице, можно утверждать, что он содержит неизвестное значение параметра Theta , то есть $PBigl{tilde{Theta}_{n}^{(1)}<Theta<tilde{Theta}_{n}^{(2)}Bigl}=1-alpha$ . Чем меньше для выбранной вероятности число $vline,tilde{Theta}_n^{(1)}-tilde{Theta}_n^{(2)}vline$ , тем точнее оценка неизвестного параметра Theta . И, наоборот, если это число велико, то оценка, проведенная с помощью данного интервала, малопригодна для практики. Так как концы доверительного интервала зависят от элементов выборки, то значения $tilde{Theta}_n^{(1)}$ и $tilde{Theta}_n^{(2)}$ могут изменяться от выборки к выборке. Вероятность p=1-alpha принято называть доверительной (надежностью). Обычно надежность оценки задается наперед, причем в качестве берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надежность, равную 0,95; 0,99; 0,999.

Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением

$P!left{overline{x}_text{v}-frac{tsigma}{sqrt{n}}<overline{x}_text{g}<overline{x}_text{v}+frac{tsigma}{sqrt{n}}right}=2Phi(t)=p,$

где — наперед заданное число, близкое к единице, а значения функции Phi(t) приведены в таблице прил. 2.

Смысл этого соотношения заключается в следующем: с надежностью можно утверждать, что доверительный интервал $left(overline{x}_text{v}-frac{tsigma}{sqrt{n}};overline{x}_text{v}+frac{tsigma}{sqrt{n}}right)$ покрывает неизвестный параметр $overline{x}_text{g}$ , точность оценки $delta=frac{tsigma}{sqrt{n}}$ . Число определяется из равенства 2Phi(t)=p , или $Phi=frac{p}{2}$ . По прил. 2 находят аргумент , которому соответствует значение функции Лапласа, равное $frac{p}{2}$ .

Пример 1. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением sigma=3 . Найти доверительные интервалы для оценки неизвестной генеральной средней по выборочным средним, если объем выборок n=36 и надежность оценки p=0,!95 .

Решение. Найдем . Из соотношения 2Phi(t)=0,!95 получим, что Phi=0,!475 . По прил. 2 находим t=1,!96 . Найдем точность оценки $delta=frac{tsigma}{sqrt{n}}=frac{1,!96cdot3}{sqrt{36}}=0,!98$ . Доверительные интервалы будут таковы: $(overline{x}_text{v}-0,!98;overline{x}_text{v}+0,!98)$ . Например, если $overline{x}_text{v}=4,!1$ , то доверительный интервал имеет следующие доверительные границы: $overline{x}_text{v}-0,!98=4,!1-0,!98=3,!12;$ $overline{x}_text{v}+0,!98=4,!1+0,!98=5,!08;$ . Таким образом, значения неизвестного параметра $overline{x}_text{g}$ , согласующиеся с данными выборки, удовлетворяют неравенству $3,!12<overline{x}_text{g}<5,!08$ .

Доверительный интервал для генеральной средней нормального распределения признака при неизвестном значении среднего квадратического отклонения задается выражением

$P!left{overline{x}_text{v}-frac{t_ps}{sqrt{n}}<overline{x}_text{g}<overline{x}_text{v}+frac{t_ps}{sqrt{n}}right}=p.$

Отсюда следует, что с надежностью можно утверждать, что доверительный интервал $left(overline{x}_text{v}-frac{t_ps}{sqrt{n}};overline{x}_text{v}+frac{t_ps}{sqrt{n}}right)$ покрывает неизвестный параметр $overline{x}_text{g}$ .

Существуют таблицы (прил. 4), пользуясь которыми, по заданным и находят вероятность и, наоборот, по заданным и находят .

Пример 2. Количественный признак генеральной совокупности распределен нормально. По выборке объема n=16 найдены выборочная средняя $overline{x}_text{v}=20,!2$ и исправленное среднеквадратическое отклонение s=0,!8 . Оценить неизвестную генеральную среднюю с помощью доверительного интервала с надежностью p=0,!95 .

Решение. Найдем . Пользуясь прил. 4 по p=0,!95 и n=16 находим tp=2,!13 . Найдем доверительные границы:

$overline{x}_text{v}-frac{t_ps}{sqrt{n}}=20,!2-frac{2,!13cdot0,!8}{sqrt{16}}=20,!2-0,!426=19,!774;$

$overline{x}_text{v}+frac{t_ps}{sqrt{n}}=20,!2+frac{2,!13cdot0,!8}{sqrt{16}}=20,!2+0,!426=20,!626.$

Итак, с надежностью p=0,!95 неизвестный параметр $overline{x}_text{g}$ заключен в доверительном интервале $19,!774<overline{x}_text{g}<20,!626$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

4.3. Оценка генеральной средней нормально распределенной совокупности

Если вы не знаете, что такое нормальное

распределение, то это, конечно, большое упущение – обязательно ознакомьтесь с материалом по ссылке. И мы сразу

разберём «заезженную» задачу, которую предлагают даже студентам-гуманитариям:

Пример 19

Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . Найти доверительный интервал для оценки математического

ожидания с надежностью 0,95, если выборочная

средняя , а объем выборки .

Прежде всего, обращаю ваше внимание на принципиальный момент: здесь

4.3.1. Известно стандартное отклонение генеральной совокупности

Дело в том, что в похожих задачах оно бывает и не известно, и тогда решение будет отличаться! Этот случай тоже будет. А

сейчас решение таково, разбираемся в ситуации:

– из генеральной совокупности проведена выборка в попугаев и по её результатам найдена выборочная

средняя: (средний рост птицы).

Выборочная средняя – это точечная оценка неизвестной нам генеральной средней . Как отмечалось выше, недостаток точечной оценки

состоит в том, что она может оказаться далёкой от истины. И по условию, требуется найти интервал , который с вероятностью накроет истинное значение .

Именно так! Здесь некорректно говорить, что «истинное значение попадёт в этот интервал». Генеральная средняя – это конкретное (пусть

и не известное нам) значение, и оно не может никуда «попасть». В разных выборках мы будем получать разные значения и разные доверительные интервалы, которые могут лишь

накрыть генеральную среднюю. А могут и не накрыть (некоторые из них).

Найдём точность оценки, она рассчитывается по формуле , где – так

называемый коэффициент доверия. Этот коэффициент отыскивается из соотношения , где – функция

Лапласа.

По условию, , следовательно:

И по таблице значений функции Лапласа либо пользуясь приложенным к курсу расчётным макетом (пункт 1*), выясняем, что значению соответствует аргумент .

Таким образом, точность оценки:

и искомый доверительный интервал:

Этот интервал с вероятностью (надёжностью) накрывает истинное генеральное значение среднего роста попугая. Но всё же остаётся 5%-ная вероятность

того, что генеральная средняя окажется вне найденного интервала.

Ответ: .

И тут возникает светлая мысль уменьшить этот интервал – чтобы получить более точную оценку. Что для этого можно сделать?

Давайте посмотрим на формулу .

Очевидно, что чем меньше стандартное отклонение (мера разброса

значений), тем уже доверительный интервал. Но это в отдельно взятой задаче ни на что не влияет – ведь нам известно

конкретное значение и изменить его невозможно.

Поэтому для уменьшения «дельты» можно уменьшить коэффициент доверия, например, вместо рассмотреть и тогда , в

результате чего доверительный интервал –

действительно стал в 2 раза короче. Но засада в том, что упала и доверительная вероятность:

пользуясь таблицей значений функции Лапласа либо расчётным макетом (пункт 1), находим: – то есть о том, что этот более узкий интервал накроет генеральную среднюю, мы

теперь можем утверждать лишь с вероятностью 68,26%. Что, конечно, неудовлетворительно, для серьёзного

статистического исследования.

Поэтому для уменьшения доверительного интервала (при том же значении ) остаётся увеличивать объём выборки . Что совершенно понятно и без формулы , ведь чем больше объём выборки, тем точнее она характеризует генеральную совокупность

(при прочих равных условиях). Об объёме выборки мы поговорим позже, ну а пока

творческая задача для самостоятельного решения:

Пример 20

По результатам выборочного исследования объектов найдена выборочная средняя .

1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения не более чем на 3,

если известно, что генеральная совокупность распределения нормально с дисперсией 400?

2) Определить доверительный интервал, который с надежностью накроет истинное значение генеральной средней.

Образец в конце книги, таблица либо расчётный

макет (пункты 1 и 1*) в помощь.

И тут, наверное, у вас назрели вопросы – а откуда известно, что генеральная совокупность распределена

нормально, и тем более, откуда известно её стандартное отклонение?

Обычно эта информация известна из предыдущих исследований. Классический пример – измерительный прибор. Очевидно, что его

случайные погрешности удовлетворяют условию теоремы Ляпунова, а значит, распределены

нормально. Кроме того, производитель, как правило, тестирует прибор, и указывает в его паспорте стандартное отклонение случайной погрешности, которое можно принять за

Но если установить нормальность распределения достаточно просто (в том числе статистическими методами), то с генеральным

значением всё сложнее – зачастую вычислить его

трудно или невозможно. В такой ситуации остаётся ориентироваться на исправленную

выборочную дисперсию и решение несколько

изменится. Возвращаемся к нашей любимой задаче:

Пример 21

В результате 10 независимых измерений некоторой величины , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в

таблице:

Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение

величины при помощи доверительного интервала,

покрывающего это значение с вероятностью 0,95.

Обратите внимание, что здесь речь идёт уже не о погрешностях прибора, а об измерениях, и помимо технических, велико

влияние других, в частности, человеческого фактора, особенно, если вы используете махрово-аналоговый инструмент – что-нибудь

вроде механического секундомера или линейки.

Решение следует начать с вычисления выборочных характеристик, и задача облегчается тем, что в Примере

13 они уже вычислены: . По условию, требуется оценить

генеральную совокупность (а именно, параметр ),

и поэтому дисперсию нужно обязательно поправить:
– несмещённая оценка неизвестной

генеральной дисперсии . И нас будет интересовать несмещённая оценка генерального стандартного отклонения :
– исправленное среднее квадратическое

отклонение.

Теперь построим доверительный интервал для оценки истинного (генерального) значения величины .

4.3.2. Если генеральная дисперсия нормального распределения не известна

то этот интервал строится по похожей формуле:

, с той поправкой, что коэффициент доверия рассчитывается с помощью распределения Стьюдента. Я

не буду рассказывать об этом распределении и ограничусь технической стороной вопроса.

Значение можно найти с помощью

таблицы значений распределения Стьюдента, в частности популярна таблица, специально

адаптированная для данной задачи*. И, согласно таблице, доверительной вероятности и объёму выборки соответствует коэффициент доверия:

* в таблице, которую можно встретить чаще, приводятся значения для так

называемого уровня значимости и для количества

степеней свободы .

Другой, более универсальный способ – воспользоваться Экселем, и чтобы далеко не ходить, я добавил этот функционал в расчётный макет: ищем пункт 2б, забиваем значения , и получаем «на выходе» .

Вычислим точность оценки:

Таким образом, искомый доверительный интервал:

– данный интервал с вероятностью накрывает истинное генеральное значение измеряемой величины .

Ответ:

Для самостоятельного решения:

Пример 22

На основании испытаний установлено, что в

среднем для изготовления шавермы полупроводникового диода требуется секунд, а исправленное среднее квадратическое отклонение составляет секунд. Предположив, что время изготовления диода есть нормальная

случайная величина, определить с надежностью доверительный интервал для оценки среднего времени изготовления диода

Краткое решение в конце книги, таблица или макет (пункт 2б) – в помощь.

Итак, что главное в разобранных задачах? Главное, обратить внимание, генеральное ли нам дано отклонение или исправленное выборочное . От этого зависит, какую формулу нужно использовать,

эту:
, где ,
или эту:
, где отыскивается с помощью распределения Стьюдента.

При увеличении объёма выборки , распределение Стьюдента стремится к нормальному распределению, и поэтому уже при во 2-м случае допускается нахождение с помощью того же соотношения . Но я бы не рекомендовал так делать. Потому что если дано , то предполагается, что решать нужно именно через «Стьюдента», и при

наличии Экселя с этим никаких проблем – можно рассчитать любые значения, которые отсутствуют в таблицах.

Коварные авторы могут предложить «простое» выборочное отклонение , и тогда его следует поправить по формуле: , которая следует из соотношения дисперсий:

. Иногда бывает предложена и дисперсия (та или

иная). Именно здесь нужно проявлять аккуратность, сами же вычисления достаточно примитивны.

4.4. Оценка генеральной дисперсии нормально распределенной совокупности

4.2 Интервальная оценка

| Оглавление |

Источник