Некоторые вычислительные особенности слау
Погрешности и
невязки
Для
оценки точности найденного решения
СЛАУ существует две общеупотребительной
меры погрешности:
-
вектор
ошибок
где


решение
Мера абсолютно точная, только для того,
чтобы ею пользоваться нужно
Чтобы избежать трудностей, вводят другую
меру
-
вектор
невязок
Невязка
— количественная мера несоответствия
между правыми и левыми частями системы
уравнений при подстановки в них
вычислительного решения.
Очевидно,
что равенство нулю вектора ошибок влечет
за собой равенство нулю вектора невязок.
Однако,
в общем случае из малости величины
невязок не следует малость ошибки. Т.е.
несмотря на то, что найденное решение

может совсем не подходить в качестве
подлинного решения. Невязка полезна в
том смысле, что с ее помощью можно
осуществить контроль точности решения.
Т.к. использовать в качестве меры контроля
вектор ошибок не представляется возможным
в виду того, что неизвестно точное
решение.
Пример.
Рассмотрим систему
Предположим,
что мы провели вычисления (неважно каким
методом) и нашли решение
Если
вычислить невязки, то невязки будут
равны
Для

10-2, но точное решение
В
общем случае можно утверждать, что для
оценки величины невязки и погрешности
можно использовать следующие формулы:
Число

матрицы А и математически оно показывает,
насколько матрица системы А близка к
вырожденной или иными словами, число
выше
тем ближе матрица к вырождению.
Обусловленность-
это внутреннее свойство матрицы СЛАУ.
Оно не связано с каким либо численным
методом. В общем случае, можно утверждать,
что матрица с большим числом обусловленности
дает большие ошибки при решении СЛАУ.
Математически
точно число обусловленности можно
вычислить.
Введем
число

Тогда
число обусловленности представляет
собой:
Тогда мы можем утверждать, что погрешность
решения:
Вычислительная
эффективность правила Крамера
Правило
Крамера широко применяется для нахождения
решения СЛУ
Если
сосчитать количество операций, которых
нам надо сделать
|
n |
3 |
10 |
20 |
|
N |
17 |
3.6*107 |
5*1019 |
|
t |
|
|
|
Численные методы
решения СЛАУ
Все
численные методы решения СЛАУ принято
делить на два класса:
-
прямые
-
итерационные
Прямые
методы используют некоторые формулы
для вычисления неизвестных величин за
конечное число шагов вычислительного
процесса
Пример.
Метод обратной матрицы
Существенным
недостатком прямых методов является
необходимость хранения в памяти
компьютера всех n- квадратных элементов
матрицы системы, т.е прямые методы
никаким образом не учитывают разряженную
структуру матрицы в системы.
Кроме
этого применения прямых методов для
решения СЛАУ с большим числом переменных
приводит к значительному накоплению
вычислительных погрешностей.
К
широко известным методам относится
метод Гаусса, метод прогонки.
Итерационные
методы ( методы последовательных
приближений)-это методы, в которых с
помощью какого- либо алгоритма строится
цепочка приближенных решений
Каждый
цикл таких вычислений называется
итерацией.
Итерационные
алгоритмы сложнее прямых методов. Объем
необходимых вычислений при их использовании
заранее трудно определить, но они не
требуеют при работе с разряженными
матрицами хранение всех ее элементов.
Более того, зачастую в них используются
вычислительные формулы, задающие эти
примеры. Итерационный процесс устроен
таким образом, что вычислительные ошибки
от итерации к итерации не накапливаются.
Поэтому итерационный метод можно
использовать как для решения хорошо
обусловленных так и плохообусловленных
СЛАУ.
Примеры:
Метод простой итерации и метод Гаусса-
Зейделя
Метод исключения
Гаусса
Хорошо
известно, что алгоритм метода Гаусса
для решения СЛАУ состоит из двух основных
шагов.
-
На
прямом ходе путем последовательного
исключения переменных из уравнений
системы, матрицу системы приводят к
треугольному виду.

верхнетреугольную матрицу:
-
На
обратном ходе вычисляется точное
решение системы

получаем:
Метод
Гаусса применим эффективно лишь в том
случае, когда матрица системы хорошо
обусловлена, имеет низкое число
обусловленности.
Точность
вычисления значительно зависит от
способа нахождения ведущего элемента,
который мы используем, для исключения
переменных на прямом ходе.
Пример.Рассмотрим систему:
Возьмем
в качестве ведущего элемента
При
решении получим:


что неправильно!
Теперь,
возьмем в качестве ведущего элемента
коэффициент перед

Тогда,

решение
Правила
для выбора ведущего элемента:
-
выбор
по столбцам
Рассматривается первый столбец.
Предполагается, что мы хотим исключить
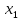
Находим в этом столбце максимальный
элемент, т.е
Находим уравнение, где коэффициент при
уравнение на первое место и используем
коэффициент при
-
выбор
по строке
Из первого уравнения находим переменную,
которую будем исключать. Ищем


которое соответствует этому максимальному
элементу. И ставим
Эту методику можно обобщить на все
элементы
-
по
всей матрице
Сканируем столбцы и строчки и ищем
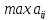
Находим
и ставим этот элемент на первое место
.
Этот прием наиболее приемлем.
Метод прогонки
Метод
прогонки является частным случаем
метода Гаусса, который специально
предназначен для решения систем уравнений
с разряженной диагональной матрицей
-
Прямой
ход состоит в том, что вычисляются
коэффициенты
Сам процесс состоит в следующем.
-
Обратная
прогонка соответствует вычислению
переменных в обратном порядке, начиная
с самого последнего x
зная

можно найти
Итерационные
методы
В общем случае схема итерационных
методов решения СЛАУ заключается в
следующем:
-
каким-
либо посторонним способом нужно
установить, какое- либо начальное
решение
-
вычисляем
правую часть:
-
находим
невязку:
-
находим
решение системы уравнений:
,
—
вектор поправок -
-
из 5.
пункта идем во 2.
Важным
вопросом является, когда нужно
остановиться!
В
качестве остановки используют какое-
либо векторное неравенство, которое
сравнивает решения, полученные на
предыдущей и последующей итерации.
Введем
норму:
Соседние файлы в папке ммм
- #
- #
11.03.20169 б13Desktop__.ini
- #
- #
- #
- #
- #
Простой пример. Система
a+b=3
a-b=1
Вы используете какой-то приближённый метод и находите приближённое решение a=1,9 и b=1,2. Находите свободные члены, какими они были бы, если бы это решение было точным. Иными словами, находим систему уравнений, для которой полученные решения будут точными.
a+b = 1,9+1,2 = 3,1
a-b = 1,9-1,2 = 0,7
Невязки равны: 3 — 3,1 = -0,1; 1 — 0,7 = 0,3.
Теперь мы решаем то же самое уравнение, только вместо свободных членов ставим невязки
a+b=-0,1
a-b=0,3
Получаем решение a=0,1; b=-0,2. Для простоты я рассматриваю случай, когда на втором шагу алгоритма получается точное решение. Хотя этот процесс может быть бесконечным, и на каждом новом шагу мы получаем поправку к предыдущему решению.
Получаем:
a0 = 1,9; a1 = 0,1; a = a0 + a1 + … = 1,9 + 0,1 + … = 2;
b0 = 1,2; b1 = -0,2; b = b0 + b1 + … = 1,2 — 0,2 + … = 1.
Невязка — величина ошибки (расхождения) приближённого равенства.
Пусть требуется найти такое x, что значение функции:
- [math]displaystyle{ f(x)=b. }[/math]
Подставив приближенное значение x0 вместо x, получаем невязку
- [math]displaystyle{ b — f(x_0) }[/math]
а ошибка в этом случае равна
- [math]displaystyle{ x — x_0 }[/math].
Если точное значение x неизвестно, вычисление ошибки невозможно, однако при этом может быть определена невязка.
Невязка аппроксимации функции
Схожее название используется в дифференциальных,
интегральных и
функциональных уравнениях.
Для аппроксимации
[math]displaystyle{ f_{rm a} }[/math] решения
[math]displaystyle{ f }[/math] уравнения
- [math]displaystyle{ T(f)(x)=g(x) }[/math] ,
невязка может быть функцией
- [math]displaystyle{ g(x)~ — ~T(f_{rm a})(x) }[/math]
или по-другому максимумом нормы разности
- [math]displaystyle{ max_{xin mathcal X} |g(x)-T(f_{rm a})(x)| }[/math] на области [math]displaystyle{ mathcal X }[/math], где функция
[math]displaystyle{ f_{rm a} }[/math]
есть усреднённое решение [math]displaystyle{ f }[/math],
или некоторый интеграл функции разности, например,
- [math]displaystyle{ int_{mathcal X} |g(x)-T(f_{rm a})(x)|^2~{rm d} x. }[/math]
В большинстве случаев, чем меньше невязка, тем аппроксимированное значение ближе к решению, то есть,
- [math]displaystyle{ left|frac{f_{rm a}(x) — f(x)}{f(x)}right| ll 1. }[/math]
В этом случае начальное уравнение принималось за корректное; и невязка могла быть использована как показатель отклонения аппроксимации от точного решения.
Использование невязок
Если точное решение неизвестно, можно использовать аппроксимацию решения с небольшой невязкой.
Невязка фигурирует во многих разделах математики, в том числе в итерационных методах, таких как метод обобщенного минимума, в котором решение системы уравнений находится путём минимизации невязки.
В навигации невязкой называется расстояние между вычисленным по прокладке местоположением судна и фактически определённым (по светилам, маякам и т.д.) местоположением, измеряется в морских милях.
Невязка — величина ошибки (расхождения) приближённого равенства.
Пусть требуется найти такое x, что значение функции:
f ( x ) = b . {displaystyle f(x)=b.}
Подставив приближенное значение x0 вместо x, получаем невязку
b − f ( x 0 ) {displaystyle b-f(x_{0})}
а ошибка в этом случае равна
x 0 − x . {displaystyle x_{0}-x.}
Если точное значение x неизвестно, вычисление ошибки невозможно, однако при этом может быть определена невязка.
Невязка аппроксимации функции
Схожее название используется в дифференциальных, интегральных и функциональных уравнениях.
Для аппроксимации f a {displaystyle f_{
m {a}}} решения f {displaystyle f} уравнения
T ( f ) ( x ) = g ( x ) {displaystyle T(f)(x)=g(x)} ,
невязка может быть функцией
g ( x ) − T ( f a ) ( x ) {displaystyle g(x)~-~T(f_{
m {a}})(x)}
или по-другому максимумом нормы разности
max x ∈ X | g ( x ) − T ( f a ) ( x ) | {displaystyle max _{xin {mathcal {X}}}|g(x)-T(f_{
m {a}})(x)|} на области X {displaystyle {mathcal {X}}} , где функция
f a {displaystyle f_{
m {a}}} есть усреднённое решение f {displaystyle f} , или некоторый интеграл функции разности, например,
∫ X | g ( x ) − T ( f a ) ( x ) | 2 d x . {displaystyle int _{mathcal {X}}|g(x)-T(f_{
m {a}})(x)|^{2}~{
m {d}}x.}
В большинстве случаев, чем меньше невязка, тем аппроксимированное значение ближе к решению, то есть,
| f a ( x ) − f ( x ) f ( x ) | ≪ 1. {displaystyle left|{frac {f_{
m {a}}(x)-f(x)}{f(x)}}
ight|ll 1.}
В этом случае начальное уравнение принималось за корректное; и невязка могла быть использована как показатель отклонения аппроксимации от точного решения.
Использование невязок
Если точное решение неизвестно, можно использовать аппроксимацию решения с небольшой невязкой.
Невязка фигурирует во многих разделах математики, в том числе в итерационных методах, таких как метод обобщенного минимума, в котором решение системы уравнений находится путём минимизации невязки.
В навигации невязкой называется расстояние между вычисленным по прокладке местоположением судна и фактически определённым (по светилам, маякам и т.д.) местоположением, измеряется в морских милях.
Невязка — уравнение
Cтраница 1
Невязка уравнения соответствует невязке (7.7) за исключением двух слагаемых.
[2]
При этом невязки уравнения (1.22), отвечающие функциям уе ( t), равномерно ограничены и почти равномерно стремятся к нулю.
[3]
Величина F представляет максимум из модулей невязок уравнений решаемых систем. Видно, что для первой системы методы 2Ф и ЧШФ приводят к приведенному выше псевдорешению. Метод РМ выполняет коррекцию параметра возмущения и обеспечивает меньшую невязку. Для первой системы коррекция проводится в нужном направлении, а для второй — в противоположном. Но это не противоречит используемой дополнительной информации при доопределении исходной некорректной задачи.
[4]
Функции Zp ( z) определяются из условий ортогональности невязки уравнений (4.1) к каждой базисной функции.
[5]
На каждой итерации метода контурных расходов уравнения материального баланса (2.2.5) удовлетворяются точно, а невязка уравнений 2-го закона Кирхгофа (2.2.25) уменьшается.
[6]
Обобщенные объемные силы Х ( г) (3.11) и Y ( r ] (3.12) в формуле (3.8) есть невязка уравнения (2.45) для заданного нулевого приближения искомых полей перемещений и потенциала электрического поля в области V квазипериодической структуры.
[7]
В алгоритме метода Ньютона, согласно итерационной формуле (8.36), матрица А представляет собой матрицу Якоби решаемой системы алгебраических уравнений F ( X) 0, а вектор В — вектор невязок уравнений этой системы.
[8]
На каждом шаге итерации взаимосвязь (2.2.10) между падением потенциала на каждой дуге и расходом по дуге учитывается точно, а поправки к APN к потенциалам вершин Р определяются так, чтобы минимизировать невязку уравнений материального баланса.
[9]
Подводя некоторые итоги истории возникновения, развития и применения увязочных методов, можно прямо сказать, что это замечательные и удивительные по своей простоте и эффективности методы, которые вобрали в себя три основные идеи упрощения и уменьшения трудоемкости вычислительных процессов: линеаризации нелинейных зависимостей; декомпозиции задачи, т.е. сведения ее к более простым сетевым операциям, и покомпонентной релаксации, когда уменьшение невязок сетевых уравнений производится их последовательной обработкой по отдельным уравнениям и переменным. Такое сочетание являлось в свое время оптимальным, так как давало, быть может, единственную возможность выполнять расчеты потокораспределения даже вручную.
[10]
При этом НР-18С используют, в частности, в режимах решения типовых экономических задач: FIN ( для оценки изменения стоимости денег при финансовых операциях), BUS ( для оценки текущего изменения стоимости), SUM ( для анализа суммарного процесса изменения стоимости со статистическим моделированием изменения одной переменной при выборе одной из четырех возможных моделей ситуаций), TIME ( изменения во времени текущих данных с вычислением оценок до шести вызывающих беспокойство ситуаций) и SOLVE для решения различных задач. В последнем режиме возможно, в частности, решение нелинейных уравнений с выводом на индикатор графика невязки уравнения в заданном масштабе с указанием курсором границ интервала нужного корня уравнения.
[11]
Соотношением для получения новых значений итерируемых переменных все время остается формула (11.20), в которой происходят соответствующие модификации матриц D и X. Причем при введении в них информации о новой точке у матрицы D появляется новая строка, соответствующая вектору невязок уравнений (11.14) на данном шаге итерации, и новый столбец, соответствующий введению нового члена в (11.17), а у матрицы X заполняется только новая строка, в которой будут храниться координаты новой точки. Если в процессе такой коррекции та или иная переменная прижимается к своей границе, то это, как правило, свидетельствует о некорректном задании этой границы.
[12]
Применительно к настоящему случаю этот метод может быть интерпретирован следующим образом. На i — й операции к значению 17Б суммируется некоторое приращение Д1 / Б, величина которого определяет невязку уравнения (5.1) в упругой и упругопластической стадиях деформирования. Процесс итераций заканчивается, когда данная невязка с заданной погрешностью равна нулю.
[13]
В современной вычислительной практике при решении как оптимизационных задач, так и задач нелинейной алгебры поправки к очередному приближению, как правило, вводятся с некоторым коэффициентом, который может быть как меньше, так и больше единицы, а конкретное его значение выбирается, исходя из некоторого критерия [253, 256] и др. Критерием обычно служит минимум той или иной нормы невязок уравнений, например, суммы их модулей или квадратов. Эффект от введения такого коэффициента состоит в том, что приближения получаются более точными и, следовательно, уменьшается число итераций. При этом, однако, использование переменного шага для приращений аргументов оправдано лишь в тех случаях, когда поиск его осуществляется намного быстрее, чем решение линеаризованной системы уравнений. Для задач большой размерности это требование обычно выполняется.
[14]
В ходе вычислений искусственные переменные исключаются. Система не имеет решения, если нельзя исключить все искусственные переменные. Число неисключенных искусственных переменных определяет невязки неудовлетворенных уравнений.
[15]
Страницы:
1
2









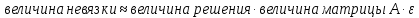

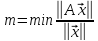


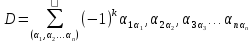






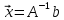




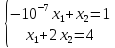

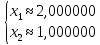










 ,
, —
—
