Что такое Невырожденный треугольник?
Что значит Невырожденный треугольник?
Вырожденный треугольник – это треугольник у которого все три вершины лежат на одной прямой. Все остальные треугольники – невырожденные.
Как определить вырожденный треугольник?
Когда у вас есть три длины сторон, a ≤ b ≤ c , треугольник вырождается, когда a + b = c . (Другие треугольники имеют a + b > c и треугольники с a + b вырожденный треугольник.
Какие бывают углы в треугольнике?
Треугольник имеет следующие углы:
- угол — угол, образованный сторонами и и противолежащий стороне ;
- угол — угол, образованный сторонами и и противолежащий стороне ;
- угол — угол, образованный сторонами и и противолежащий стороне .
Как появилась фигура треугольник?
В нашей стране, треугольник появился около 1775 года, благодаря своему экзотическому, восточному колориту. Впервые он прозвучал в опере Грэтри «Тайная магия». Известно, что в оркестрах военной музыки он возник гораздо раньше. Так, в России, в дореволюционные времена, он был популярен в войсках Елизаветы Петровны.
Какие треугольники бывают по сторонам?
Виды треугольников по сторонам:
Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны. Равнобедренный треугольник — это треугольник, у которого две стороны равны. Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
Как узнать существует ли треугольник?
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится. Пользователь вводит длины трех сторон.
Как узнать существует ли треугольник со сторонами?
Чтобы треугольник существовал, сумма двух сторон треугольника всегда должна быть больше третей стороны. a + b > c, b + c > a, a + c > b.
Как определить вид треугольника по его сторонам?
Если выполняется теорема Пифагора: с²=a²+b² , где с — наибольшая сторона, а и b две других, – треугольник прямоугольный. Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² треугольник остроугольный.
Как определить существует ли треугольник с такими сторонами?
Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.
Как правильно обозначать углы в треугольнике?
Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C. Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак .
Какие виды треугольников бывают по углам и сторонам?
Виды треугольников
- Существует три вида треугольников по углам:
- Прямоугольный треугольник содержит прямой угол. .
- Тупоугольный треугольник содержит тупой угол. .
- Виды треугольников по сторонам:
- Равносторонний треугольник – это треугольник, у которого все стороны равны.
Как доказать что фигура треугольник?
Чтобы проверить, могут ли заданные три отрезка a, b и c образовать треугольник, достаточно проверить будет ли самый длинный отрезок меньше суммы длин двух других отрезков. Сумма углов любого треугольника равна 180∘. Подробнее в теореме о сумме углов треугольника.
Как доказать что это равнобедренный треугольник?
Признаки равнобедренного треугольника
- Если в некотором треугольнике два угла равны, то он – равнобедренный;
- Если в некотором треугольнике совпадают: а) высота и биссектриса или б) высота и медиана или в) медиана и биссектриса, проведённые к одной стороне, то такой треугольник – равнобедренный.
Как найти угол треугольника если известны 2 стороны?
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d9f33d6b8b27a7d • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Определить существование треугольника по трем сторонам
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.
Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной c , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
Можно решить задачу сложнее. Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:
Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует. Большего внимания заслуживает использование вложенных конструкций if-else.
http://mathvox.ru/geometria/treugolniki/treugolniki-glava-1/virojdennii-treugolnik-i-dlina-storoni/
http://younglinux.info/python/task/triangle
Для более полного ответа на этот вопрос, следует дать определение вырожденного треугольника. Это такой треугольник, у которого все стороны лежат на одной прямой.
У вырожденного треугольника вершины всех его углов совпадают.
Основным свойством такого треугольника, вытекающим из неравенства треугольника, является следующее — длина самой длинной стороны вырожденного треугольника равна половине его периметра.
В вырожденном треугольнике сумма двух сторон всегда равна по величине его третьей стороне.
Все остальные треугольники, у которых все три стороны не лежат на одной прямой, являются невырожденными. У них стороны в вершинах образуют три угла.
Другое определение невырожденного треугольника — многоугольник, у которого имеется только три угла.
У такого треугольника сумма любых двух сторон всегда больше третьей стороны.
Содержание
- Что такое Невырожденный треугольник?
- Что такое Невырожденный треугольник?
- Какие есть виды треугольников?
- Чему равны стороны треугольника?
- Какой знак имеет косинус тупого угла а?
- Что такое тангенс тупого угла?
- Что такое косинус?
- Как найти tg cos sin?
- Вырождение (математика) — Degeneracy (mathematics)
- СОДЕРЖАНИЕ
- В геометрии
- Коническое сечение
- SPMISCIENCE
- Треугольник
- Треугольник
- [править] Свойства и особенности треугольников
- [править] Обозначения
- [править] Признаки равенства треугольников
- [править] Типы треугольников
- [править] По величине углов
- [править] По числу равных сторон
- [править] Определения, связанные с треугольником
- [править] Окружности
- [править] Лучи, отрезки и точки
- [править] Соотношения в треугольнике
- [править] Неравенство треугольника
- [править] Теорема о сумме углов треугольника
- [править] Теорема синусов
- [править] Прочие соотношения
- [править] Площадь треугольника
- [править] Вычисление площади треугольника в пространстве с помощью векторов
- [править] См. также
Что такое Невырожденный треугольник?
Что такое Невырожденный треугольник?
е. как часть плоскости, ограниченную тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. . Иногда рассматривают вырожденный треугольник, три вершины которого лежат на одной прямой. Если не оговорено иное, треугольник в данной статье предполагается невырожденным.
Какие есть виды треугольников?
Существует три вида треугольников по углам: остроугольные; прямоугольные; тупоугольные.
Чему равны стороны треугольника?
Треугольник – это многоугольник с тремя сторонами (или тремя углами). . 23 ) — равнобедренный, если две его стороны равны ( a = c ); эти равные стороны называются боковыми, третья сторона называется основанием треугольника. Треугольник ABC ( рис. 24 ) – равносторонний, если все его стороны равны ( a = b = c ).
Какой знак имеет косинус тупого угла а?
Тупой угол это вторая четверть, значит котангенс отрицательный, знак минус.
Что такое тангенс тупого угла?
Тангенс — отношение противолежащего катета к прилежащему. Тангенс острого угла = 3/1 = 3. Это получается если достроить мысленно сбоку угол до прямоугольного треугольника. Тангенс тупого угла равен тангенсу острого угла, только с минусом.
Что такое косинус?
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе. В нашем треугольнике cos beta =frac. Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
Как найти tg cos sin?
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
- Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
- Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Источник
Вырождение (математика) — Degeneracy (mathematics)
В математике , вырожденный случай является предельным случаем класса объектов , которые , как представляется, качественно отличаются от (и , как правило , проще , чем) остальной части класса, а термин вырождение является условием является вырожденным случаем.
Определения многих классов составных или структурированных объектов часто неявно включают неравенства. Например, углы и длины сторон треугольника должны быть положительными. Предельные случаи, когда одно или несколько из этих неравенств становятся равенствами, являются вырождениями. В случае треугольников получается вырожденный треугольник, если хотя бы одна сторона или угол равны нулю (эквивалентно, он становится «отрезком линии»).
Часто вырожденные случаи являются исключительными случаями, когда происходят изменения обычной размерности или мощности объекта (или какой-либо его части). Например, треугольник — это объект размерности два, а вырожденный треугольник содержится в линии , что делает его размерность равной единице. Это похоже на случай круга, размер которого уменьшается с двух до нуля, когда он превращается в точку. В качестве другого примера, набор решений из системы уравнений , которая зависит от параметров , как правило , имеет фиксированную мощность и размер, но количество элементов и / или размер могут быть различными для некоторых исключительных значений, называется вырожденные случаи. В таком вырожденном случае множество решений называется вырожденным.
Для некоторых классов составных объектов вырожденные случаи зависят от конкретно исследуемых свойств. В частности, класс объектов часто может быть определен или охарактеризован системами уравнений. В большинстве сценариев данный класс объектов может определяться несколькими различными системами уравнений, и эти разные системы уравнений могут приводить к различным вырожденным случаям, характеризуя одни и те же невырожденные случаи. Это может быть причиной отсутствия общего определения вырождения, несмотря на то, что это понятие широко используется и определяется (при необходимости) в каждой конкретной ситуации.
Таким образом, у вырожденного случая есть особые особенности, которые делают его нетипичным . Однако не все необщие случаи вырождены. Например, прямоугольные , равнобедренные и равносторонние треугольники не являются общими и невырожденными. Фактически, вырожденные случаи часто соответствуют особенностям объекта или некоторого конфигурационного пространства . Например, коническое сечение является вырожденным тогда и только тогда, когда оно имеет особые точки (например, точка, прямая, пересекающиеся прямые).
СОДЕРЖАНИЕ
В геометрии
Коническое сечение
Вырожденная коника — это коническое сечение ( плоская кривая второй степени , определяемая полиномиальным уравнением второй степени), которое не может быть неприводимой кривой .
- Точка является вырожденной окружности , а именно один с радиусом 0.
- Линия представляет собой вырожденный случай параболы , если парабола находится на касательной плоскости . В инверсивной геометрии линия представляет собой вырожденный случай окружности с бесконечным радиусом.
- Две параллельные прямые также образуют вырожденную параболу.
- Отрезок линии можно рассматривать как вырожденный случай эллипса, в котором малая полуось стремится к нулю, фокусы идут к конечным точкам, а эксцентриситет переходит к единице.
- Круг можно рассматривать как вырожденный эллипс, поскольку эксцентриситет приближается к 0.
- Эллипс также может вырождаться в одну точку.
- Гипербола может вылиться в две строк , пересекающихся в точке, через семейство гипербол , имеющие эти линии , как общие асимптоты .
Источник
SPMISCIENCE
Треугольник
Треугольник
[править] Свойства и особенности треугольников
Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости. [1]
Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.
Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.
Треугольник, когда не вырожден — всегда выпуклый многоугольник.
Для треугольника всегда существует одна вписанная и одна описанная окружность.
[править] Обозначения
Точки вершин треугольника традиционно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α, β, γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c).
[править] Признаки равенства треугольников
Треугольник однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:
- a, b, γ (равенство по двум сторонам и углу лежащему между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам);
- a, b, c (равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
[править] Типы треугольников
| Типы треугольников | ||
|---|---|---|
 Остроугольный |
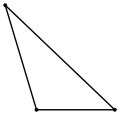 Тупоугольный |
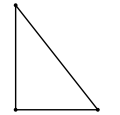 Прямоугольный |
 Разносторонний |
 Равнобедренный |
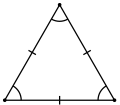 Равносторонний |
[править] По величине углов
сумма углов треугольника равна 180°.
Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
[править] По числу равных сторон
- Разносторонним называется треугольник, у которого длины трёх сторон различны.
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
- Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностейсовпадают.
[править] Определения, связанные с треугольником
[править] Окружности
- Вписанная окружность — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром.
- Описанная окружность — окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
- Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон.
[править] Лучи, отрезки и точки
- Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.
- Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
- Биссектрисой треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).
- Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника.
В равнобедренном треугольнике биссектриса, медиана и высота, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.
Серединные перпендикуляры(медиатриссы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.
Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек.
В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности девяти точек лежат на одной прямой, называемой прямой Эйлера.
Ортоцентр, инцентр, центроид (центр тяжести), а также некоторые другие точки называются замечательными точками треугольника.
[править] Соотношения в треугольнике
[править] Неравенство треугольника
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон невырожденного треугольника связаны следующими неравенствами.
[править] Теорема о сумме углов треугольника
[править] Теорема синусов
где R — радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a
[править] Прочие соотношения
Метрические соотношения в треугольнике приведены для треугольника 
Где:
- aL,bL — отрезки, на которые биссектриса
делит сторону
,
- ma,mb,mc — медианы, проведённые соответственно к сторонам a, b и c,
- ha,hb,hc — высоты, опущенные соответственно на стороны a, b и c,
- r — радиусвписанной окружности,
- R — радиусописанной окружности,
— полупериметр,
- S — площадь,
- d — расстояние между центрами вписанной и описанной окружностей.
[править] Площадь треугольника
, так как
, то:
— формула Герона
— для прямоугольного треугольника
— для равностороннего треугольника
— если треугольник задан по стороне и двум прилежащим к ней углам
— если треугольник задан по стороне и двум прилежащим к ней углам
Где:
Для площади справедливы неравенства:
[править] Вычисление площади треугольника в пространстве с помощью векторов
Пусть вершины треугольника находятся в точках 


Введём вектор площади 
Положим 



Площадь треугольника равна 
Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона.
[править] См. также
В Викисловаре есть статья «треугольник»
Источник
|
0 / 0 / 0 Регистрация: 21.11.2010 Сообщений: 3 |
|
|
1 |
|
Невырожденный треугольник30.11.2010, 20:47. Показов 18848. Ответов 8
Дан набор из N отрезков различной длины. Сколькими способами можно выбрать из этих отрезков три, из которых можно составить (невырожденный) треугольник? Программа должна вывести одно число — искомое количество способов. Собственно вопрос в следующем:
0 |
|
Day 1177 / 987 / 83 Регистрация: 29.10.2009 Сообщений: 1,385 |
||||
|
01.12.2010, 20:22 |
2 |
|||
ЗЫ. Интересно было бы обобщить эту задачу для m-угольников (m >=3) Добавлено через 1 минуту
1 |
|
Напильнег 481 / 119 / 17 Регистрация: 30.09.2010 Сообщений: 473 |
||||
|
01.12.2010, 22:31 |
3 |
|||
|
А можно, кстати, нехило извратиться, записав условие во внутреннем цикле в естественной форме:
2 |
|
1177 / 987 / 83 Регистрация: 29.10.2009 Сообщений: 1,385 |
|
|
01.12.2010, 23:55 |
4 |
|
Напильнег, идея симпатичная.
0 |
|
481 / 119 / 17 Регистрация: 30.09.2010 Сообщений: 473 |
|
|
02.12.2010, 01:14 |
5 |
|
РешениеЛениво…
0 |
|
1177 / 987 / 83 Регистрация: 29.10.2009 Сообщений: 1,385 |
|
|
02.12.2010, 02:26 |
6 |
|
Лениво… А никто тебя с печки слезать не заставляет.
0 |
|
Manjak 270 / 176 / 46 Регистрация: 12.03.2010 Сообщений: 494 |
||||||||
|
02.12.2010, 09:54 |
7 |
|||||||
|
Вроде все точно
Добавлено через 20 минут
0 |
|
Day 1177 / 987 / 83 Регистрация: 29.10.2009 Сообщений: 1,385 |
||||
|
02.12.2010, 12:48 |
8 |
|||
|
Ну вот, кажется, получилось
Запуск
1 |
|
0 / 0 / 0 Регистрация: 21.11.2010 Сообщений: 3 |
|
|
03.12.2010, 22:13 [ТС] |
9 |
|
развили идею, всем спасибо)
0 |
Содержание
- — Как узнать существует ли треугольник со сторонами?
- — Как определить Невырожденный треугольник?
- — Как проверить есть ли треугольник?
- — В каком случае может существовать треугольник?
- — Как проверить существует ли равнобедренный треугольник?
- — Какой нельзя построить треугольник?
- — Как определить можно ли из отрезков составить треугольник?
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится. Пользователь вводит длины трех сторон.
Как узнать существует ли треугольник со сторонами?
Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.
Как определить Невырожденный треугольник?
Вырожденный треугольник – это треугольник у которого все три вершины лежат на одной прямой. Все остальные треугольники – невырожденные.
Как проверить есть ли треугольник?
Чтобы треугольник существовал, сумма двух сторон треугольника всегда должна быть больше третей стороны. a + b > c, b + c > a, a + c > b.
В каком случае может существовать треугольник?
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей. … Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.
Как проверить существует ли равнобедренный треугольник?
Треугольник является разносторонним, если все его стороны имеют разную длину; треугольник будет равнобедренным, если любые две его стороны равны между собой, но отличны от третьей; и треугольник является равносторонним, когда все его стороны равны.
Какой нельзя построить треугольник?
Если большая сторона меньше суммы двух других сторон, то треугольник построить можно. 1) а = 1 см; b = 2 см; с = 3 см, 3 < 1 + 2 — неверно, значит треугольник построить нельзя.
Как определить можно ли из отрезков составить треугольник?
Чтобы из трех отрезков можно было составить треугольник, необходимо и достаточно, чтобы сумма длин любых двух отрезков была строго больше третьего.
Интересные материалы:
Сколько стоит Спотифай?
Сколько стоит участие в шоу Голос дети?
Сколько стоит укладка паркета?
Сколько стоит утеплить мансардную крышу?
Сколько стоит ужин в поезде?
Сколько стоит вязальная проволока для арматуры?
Сколько стоит вилла в Испании?
Сколько стоит водоэмульсионная краска?
Сколько стоит выровнять пол под ламинат?
Сколько стоит Xiaomi Redmi 5 32gb?






 делит сторону
делит сторону  ,
, — полупериметр,
— полупериметр,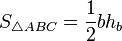 , так как
, так как  , то:
, то:

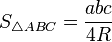
 — формула Герона
— формула Герона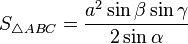

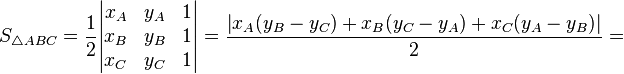

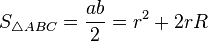 — для прямоугольного треугольника
— для прямоугольного треугольника — для равностороннего треугольника
— для равностороннего треугольника — если треугольник задан по стороне и двум прилежащим к ней углам
— если треугольник задан по стороне и двум прилежащим к ней углам — если треугольник задан по стороне и двум прилежащим к ней углам
— если треугольник задан по стороне и двум прилежащим к ней углам



 Сообщение было отмечено как решение
Сообщение было отмечено как решение
