Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:
- множество X содержит хотя бы одно неотрицательное число;
- все элементы множества X отрицательны.
Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие eqref{ref1}. Пусть C=c0,c1c2…cn…; тогда c0 — неотрицательное целое число, причем C < c0+1, где c0+1 = n0 ∈ (mathbb{N}). Следовательно, $$forall xin X rightarrow x < C < n_0.label{ref5}$$
Если x=a0,a1a2…=a0,{an} — произвольный элемент множества X, то из eqref{ref5} следует, что 0 ≤ a0 < n0. Рассмотрим множество E целых частей элемента множества X. Так как E — конечное непустое множество целых неотрицательных чисел, то в этом множестве есть наибольший элемент ({overline a}_0). Обозначим,$$X_0=left{xin X: x={overline a}_0,left{a_nright}right}.nonumber$$
Множество X0 состоит из всех тех элементов множества X, у которых целая часть равна ({overline a}_0); множество X0 непустое и X ⊃ X0.
Пусть E1 — множество первых десятичных знаков элементов множества X0. Так как множество E1 конечно (его элементы могут быть числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и непусто, то существует ({overline a}_1=underset{xin X_0}{max} a_1) — наибольший из первых десятичных знаков элементов множества X0.
Пусть (X_1=left{xin X: x={overline a}_0,{overline a}_1a_2…right}); тогда X ⊃ X0 ⊃ X1. Обозначим ({overline a}_2=underset{xin X_1}{max} a_2) наибольший из вторых десятичных знаков элементов множества X1,$$X_2=left{xin X_1: a_2={overline a}_2right}=left{xin X: x={overline a}_0,{overline a}_1{overline a}_2a_3…right}.nonumber$$
Продолжая эти рассуждения, построим последовательность {Xk} непустых множеств и последовательность десятичных знаков ({overline a}_k) таких, что X ⊃ X0 ⊃ X1 ⊃ … X ⊃ X0 ⊃ …,$${overline a}_k=underset{xin X_{k-1}}{max} a_k,nonumber$$
$$X_k=left{xin X_{k-1}: a_k={overline a}_kright}=left{xin X: x={overline a}_0,{overline a}_1…{overline a}_ka_{k+1}…right}nonumber$$
Рассмотрим десятичную дробь (overline x={overline a}_0,{overline a}_1{overline a}_2…={overline a}_0,left{{overline a}_nright}). Покажем, что x = sup X, то есть что
$$forall xin X rightarrow x leq overline x,label{ref6}$$
$$forall x’ < overline x existswidetilde xin X: widetilde x > x’.label{ref7}$$
Возьмем произвольное число x ∈ X и пусть x = a0,{an}. Чтобы проверить выполнение условия eqref{ref6}, рассмотрим три произвольных случая:
$$xnotin X_k при k=0,1,2,…,label{ref8}$$
$$xin X_k при k=0,1,2,…,label{ref9}$$
$$exists m: xin X_{m-1}, xnotin X_{m.}label{ref10}$$
Из eqref{ref8} следует, что (a_0 < {overline a}_0) и поэтому (x < overline x). Если выполнено условие eqref{ref9}, то (a_k={overline a}_k) при k = 0, 1, 2,…, откуда, по определению числа (overline x), справедливо равенство (x=overline x). Наконец из eqref{ref10}, согласно определению множества Xm и числа (x=overline x), следует, что
$$x = {overline a}_0,{overline a}_1…{overline a}_{m-1}a_m… <{overline a}_0,{overline a}_1…{overline a}_{m-1}{overline a}_m(0) leq overline x,nonumber$$
и поэтому (x < overline x). Таким образом, неравенство eqref{ref6} доказано.
Проверим условие eqref{ref7}. Если x’ < 0, то eqref{ref7} имеет место при любом (widetilde xin X), т.к. все элементы множества X неотрицательны.
Пусть (0 leq x’ leq overline x) и (x’=a’_0,left{a’_nright}). Тогда либо (a’_0 < {overline a}_0), либо (a’_k=a_k при k=overline{0, m-1},a’_m < {overline a}_m). В первом случае в качестве (widetilde x) можно взять любой элемент множества X0, так как из условий (a’_0 < {overline a}_0) и (widetilde xin X_0) следует, что
$$x’ < widetilde x={overline a}_0,a_1…a_n… leq overline x, то есть x’ < widetilde x leq overline x и xin X_0subset X.nonumber$$
Во втором случае условию eqref{ref7} удовлетворяет произвольный элемент (widetilde xin X_m), так как
$$x’={overline a}_0,{overline a}_1…{overline a}_{m-1}a’_m… < {overline a}_0,{overline a}_1…{overline a}_{m-1}{overline a}_ma_{m+1}…=widetilde x leq overline x.nonumber$$
Таким образом, (x’ < widetilde x leq overline x), где (widetilde xin X_msubset X). Условие eqref{ref7} проверено.
Итак, условия eqref{ref6} и eqref{ref7} выполняются, то есть x = sup X. То есть мы доказали предположение, что существует точная верхняя грань при предположении, что все элементы множества X неотрицательны.
Если множество X содержит хотя бы один неотрицательный элемент x0 ≥ 0, то множество (left{widetilde X=xin X: x geq x_0right}) состоит из неотрицательных чисел, причем (sup X=sup widetilde X). Поэтому непустое ограниченное сверху числовое множество X имеет точную верхнюю грань.
Второй случай. Если все элементы множества X отрицательны, то произвольный элемент x ∈ X записываются в виде
$$x=-a_0,a_1a_2…a_n…label{ref11}$$
Пусть (a_0^ast) — наименьшее из чисел a0 в записи eqref{ref11} для всех x ∈ X, (a_1^ast) — наименьший из первых десятичных знаков тех элементов множества X, у которых (a_0=a_0^ast); (a_2^ast) — наименьший из вторых десятичных знаков тех элементов множества X, у которых (a_0=a_0^ast, a_1=a_1^ast) и т.д. Указанным способом определяется число (x^ast=-a_0^ast,a_1^ast…a_n^ast…=-a_0^ast,left{a_n^astright}). По аналогии с первым случаем доказывается, что число x* является точной верхней гранью множества.
Множество, элементами которого являются вещественные числа, будем называть числовым. Если множество состоит из конечного числа элементов, то его называют конечным, в противном случае – бесконечным.
Определение. Числовое множество называется ограниченным сверху, если существует такое вещественное число
, что для любого элемента
из множества
выполняется неравенство
. Число
называется верхней границей
.
Определение. Если существует такое число , что все элементы множества
удовлетворяют неравенству
, то множество
называется ограниченным снизу, а число
– его нижней границей.
Определение. Числовое множество называется ограниченным, если оно ограничено сверху и снизу, т. е. если для всех
выполняется неравенство
.
Если – верхняя, а
– нижняя границы множества
, то числа
и
тоже будут соответственно верхней и нижней границами этого множества. Следовательно, всякое ограниченное множество имеет бесконечно много верхних и нижних границ.
Определение. Наименьшая из всех верхних границ множества называется точной верхней границей этого множества (обозначается
). Наибольшая из всех нижних границ
называется точной нижней границей этого множества (обозначается
).
Точная верхняя и точная нижняя границы могут как принадлежать данному множеству, так и не принадлежать ему.
Если не ограничено сверху, то пишут
, если снизу, то
.
На вопрос о том, всегда ли у ограниченного множества существуют точные границы, отвечает следующая теорема.
Теорема. Всякое непустое ограниченное сверху множество имеет точную верхнюю границу, а всякое непустое ограниченное снизу множество имеет точную нижнюю границу.
Пример 1. Даны множества ,

. Указать их точные границы.
Решение. – бесконечное, ограниченное снизу множество. Числа
– его нижние границы, а
. Сверху это множество не ограничено, т. е.
. Множество
– бесконечное ограниченное множество, т. е. оно ограничено и сверху, и снизу, его точные границы:
,
,
– бесконечное множество, не ограниченное как сверху, так и снизу.
Любое конечное множество ограничено, так как среди его элементов всегда найдутся наибольшее и наименьшее числа, которые и будут точными границами. Обратное утверждение неверно, т. е. из ограниченности множества не следует его конечность, как это видно на примере множества .
Пример 2. Числовое множество состоит из всех чисел, для которых
. Какие числа будут его границами?
Решение. Неравенство равносильно двойному неравенству
, откуда видно, что число 3 и всякое большее число будет верхней границей, а число –3 и всякое меньшее число – его нижней границей.
,
.
Пример 3. Числовое множество состоит из чисел, удовлетворяющих условию
. Укажите наименьшее число
, удовлетворяющее неравенству
для всех
из данного множества. Какими границами для этого множества будут числа
и
?
Решение. Так как равносильно неравенству
, то за
нужно взять такое положительное число, чтобы неравенства:
и
выполнялись одновременно. Это, очевидно, будет при
, равном наибольшей из абсолютных величин чисел
и
, то есть при
, при этом
, a
– верхняя (не точная) граница
, точной верхней границей является
.
Вопросы для самопроверки.
1. Приведите примеры ограниченных бесконечных множеств. Существуют ли конечные неограниченные множества?
2. Приведите примеры множеств, которым принадлежат их точные границы и множеств, которым не принадлежат их точные границы.
3. Приведите пример множества, которому принадлежит его точная нижняя граница, а точная верхняя не принадлежит.
| < Предыдущая | Следующая > |
|---|
Действительные числа изображаются, как
известно, точками числовой прямой,
причем каждому действительному числу
соответствует одна точка числовой
прямой и обратно, каждой точке числовой
прямой соответствует только одно
действительное число. Как говорят,
установлено взаимно-однозначное
соответствие между множеством точек
числовой прямой и множеством действительных
чисел. Поэтому, говоря о числовых
множествах, мы будем иметь в виду как
подмножества множества R
действительных чисел, так и подмножества
точек числовой прямой.
Определение 1. МножествоЕ
действительных чисел называетсяограниченным сверху (соответственно,ограниченным снизу), если
существует числоМ, такое, что для
любогоимеет место неравенство
(соответственно,
).
ЧислоМ называетсяверхней
(соответственно,нижней)границей (или гранью) множестваЕ. МножествоЕ называетсяограниченным, если существуют
такие числаи
,
что для любого числаимеет место двойное неравенство
.
Например, множество правильных дробей
ограничено сверху числом 1, множество
N натуральных
чисел ограничено снизу числом 1, множествоограничено, так как
.
Заметим, что если М– верхняя граница
непустого ограниченного сверху числового
множестваЕ, то любое число, большееМ, также будет его верхней границей,
то есть уЕ есть бесконечное
множество верхних границ. Из всех верхних
границ множестваЕ наибольший
интерес представляет его наименьшая
верхняя граница.
Определение 2. Наименьшая из верхних
границ множестваЕ называется еготочной верхней границей (или
точной верхней гранью) и обозначаетсяsup E
(от латинского словаsupremum– наивысшее).
Аналогично вводится понятие точной
нижней границы множества Е,
ограниченного снизу.
Определение 3. Наибольшая из нижних
границ множестваЕ называется еготочной нижней границей (или
точной нижней гранью) и обозначаетсяinf E
(от латинского словаinfimum– наинизшее).
Имеет место
Теорема 1. Всякое непустое и
ограниченное сверху (соответственно,
снизу) числовое множествоЕ имеет
точную верхнюю (соответственно, нижнюю)
границу.
Доказательство. Проведем его для
случая верхней границы. Рассмотрим два
случая.
1) Предположим сначала, что среди чисел
х множестваЕ найдется
наибольшее.
Тогда все числа множества будут
удовлетворять неравенству,
т.е.– верхняя граница множестваЕ. С
другой стороны, поскольку,
то для любой верхней границыМ
выполняется неравенство.
Отсюда следует, что–
точная верхняя граница множестваЕ.
2) Пусть теперь среди чисел х множестваЕ нет наибольшего. Произведем
сечение множестваR
действительных чисел следующим
образом. К верхнему классуотнесем все верхние границы
множестваЕ, а к нижнему классуА
все остальные действительные числа.
При этом все числапопадут в классА, так как среди них
нет наибольшего. По теореме Дедекинда
существует действительное число,
производящее данной сечение. Все числа,
как принадлежащие классуА, не
превосходят этого пограничного числа,
т.е.– верхняя граница множестваЕ, т.е.
и является в
наименьшим числом по теореме Дедекинда.
Поэтому.
Аналогично доказывается вторая часть
теоремы о существовании точной нижней
границы (это могут сделать студенты
дома самостоятельно). Теорема доказана.
Из школьного курса математики известны
некоторые специальные числовые множества:
–интервал(открытый промежуток),
–отрезок(замкнутый промежуток),
,
–полуинтервалы(открытый справа
и слева соответственно),–
вся числовая прямая,– лучи. Отрезки, интервалы и полуинтервалы
называютсяпромежутками.
Определение 4. Еслиа– некоторое
действительное число,– любое положительное действительное
число, то интервалназывается
—окрестностьюточкиа. Точкааназываетсяцентромокрестности, а число
—радиусомокрестности. Множество
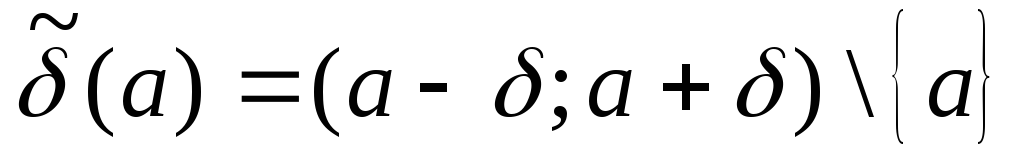
—
окрестностью точкиа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ограниченность числовых множеств, их точные границы. Предельные точки числовых множеств.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пусть $X -$ произвольное непустое множество действительных чисел. Число $M=max X$ называется наибольшим (максимальным) элементом множества $X,$ если $Min X$ и для всякого $xin X$ выполняется неравенство $xleq M$. Аналогично определяется понятие наименьшего (минимального) элемента $m=min X$ множества $X.$
Множество $X$ называется ограниченным сверху, если существует действительное число $a$ такое, что $xleq a$ для всех $xin X.$ Всякое число, обладающее этим свойством, называется верхней гранью множества $X.$ Для заданного ограниченного сверху множества $X$ множество всех его верхних граней имеет наименьший элемент, который называется точной верхней гранью множества $X$ и обозначается символом $sup X.$ Очевидно $sup X=max X$ тогда и только тогда когда $sup Xin X.$
Аналогично определяются понятия ограниченного снизу множества, нижней грани и точной нижней грани множества $X.$ Последняя обозначается символом $inf X.$
Множество $X,$ ограниченное снизу и сверху, называется ограниченным.
Пусть $xsubset R.$ Число $x_0in R$ называется предельной точкой множества X, если любая окрестность точки $x_0$ содержит точку из множества $X,$ отличную от $x_0,$ то есть для $$forallvarepsilon>0,,exists yin X, yneq x_0: |y-x_0|<varepsilon.$$
Сама точка $x_0$ может принадлежать, а может и не принадлежать множеству $X$.
Примеры.
1.73. Пусть $X=left{1, frac{1}{2}, frac{1}{3}, frac{1}{n}right}.$
а) Указать наименьший и наибольший элементы этого множества, если они существуют.
б) Каковы множества верхних и нижних граней для множества $X.$ Найти $sup X$ и $inf X.$
Решение.
а) Данное множество имеет наибольший элемент $M=1$ поскольку для всех элементов множества $xin X $ выполняется неравенство $xleq 1$ и при этом $1in X.$
Наименьшего элемента заданное множество не имеет, так как для любого элемента $x_n=frac{1}{n}in X$ всегда найдется элемент $x_{n+1}=frac{1}{n+1}in X$ для которого выполняется неравенство $x_{n+1}leq x_n.$
б) Поскольку для всех элементов $x$ множества $X$ выполняется неравенство $xleq 1,$ причем $1in X,$ то множество верхних граней для множества $X$ это множество $[1, +infty)$ c наименьшим элементом равным $1.$ Таким образом, $sup X=1.$
Наименьшего элемента множества $X$ не существует. Очевидно, что для всех элементов $x$ множества $X$ выполняется $xgeq 0, $ то есть множество $X$ ограничено снизу. Покажем, что $0$ является предельным значением множества $X.$ Действительно, для любого $varepsilon>0$ можно найти натуральное число $$n>frac{1}{varepsilon},,Rightarrow,,frac{1}{n}<varepsilon,quadfrac{1}{n}in X.$$ Таким образом, множество нижних граней для $X$ это множество $(-infty, 0]$ c наибольшим элементом равным $0.$ Отсюда находим $inf X=0.$
Ответ: $M=1,$ наименьшего элемента не существует, $[1, +infty),$ $(-infty, 0],$ $sup X=1,$ $inf X=0.$
1.74. Для множества $X=left{xin R|,, x=frac{1}{2^n},,, nin Nright}$ найти $max X, ,, min X,$ $sup X$ и $inf X$ если они существуют.
Решение.
Запишем множество $X$ в виде
$$X=left{xin R|,, x=frac{1}{2^n},,, nin Nright}=left{frac{1}{2},frac{1}{4}, frac{1}{8}, .., frac{1}{2^n},…right}$$
Данное множество имеет наибольший элемент $M=frac{1}{2}$ поскольку для всех элементов множества $xin X $ выполняется неравенство $xleq frac{1}{2}.$ При этом $frac{1}{2}in X.$
Наименьшего элемента заданное множество не имеет, так как для любого элемента $x_n=frac{1}{2^n}in X$ всегда найдется элемент $x_{n+1}=frac{1}{2^{n+1}}in X$ для которого выполняется неравенство $x_{n+1}leq x_n.$
Поскольку для всех элементов $x$ множества $X$ выполняется неравенство $xleq frac{1}{2},$ причем $frac{1}{2}in X,$ то множество верхних граней для множества $X$ это множество $left[frac{1}{2}, +inftyright)$ c наименьшим элементом равным $frac{1}{2}.$ Таким образом, $sup X=frac{1}{2}.$
Наименьшего элемента множества $X$ не существует. Очевидно, что для всех элементов $x$ множества $X$ выполняется $xgeq 0, $ то есть множество $X$ ограничено снизу. Покажем, что $0$ является предельным значением множества $X.$ Действительно, для любого $varepsilon>0$ можно найти натуральное число $$n>log_2frac{1}{varepsilon},,Rightarrow 2^n>frac{1}{varepsilon}Rightarrow,,frac{1}{2^n}<varepsilon,quadfrac{1}{2^n}in X.$$Таким образом, множество нижних граней для $X$ это множество $(-infty, 0]$ c наибольшим элементом равным $0.$ Отсюда находим $inf X=0.$
Ответ: $M=frac{1}{2},$ наименьшего элемента не существует $sup X=frac{1}{2},$ $inf X=0.$
1.80. Пусть $Xsubset R -$ произвольное ограниченное множество. Доказать, что множество $-X={x|,, -xin X}$ так же ограничено и справедливы равенства $$sup (-X)=-inf X,qquad inf (-X)=-sup X.$$
Доказательство.
Так как множество $X$ ограничено, то оно ограничено сверху и снизу, а значит существуют соответственно, числа $a$ и $b$ такие, что $forall xin X, ,, aleq xleq b. $ Отсюда, решая неравенство видно, что для элементов $-x$ верно неравенство $-bleq -xleq -a.$ То есть множество $-X={x|,, -xin X}$ также является ограниченным.
Пусть $a=inf X.$ Тогда из неравенства $-xleq -a$ получаем $-xleq -inf X.$
Если $ain X,$ то $-ain -X.$ В этом случае очевидно, что $$-a=sup(-X)Rightarrow sup(-X)=-inf X.$$
Если $anotin X,$ то $-anotin -X.$ Покажем, что $-a$ это наименьшй элемент принадлежащий множеству верхних граней. Действительно, пусть существует элемент $cneq a, ,,-cnotin -X,$ такой что для всех $-xin -X$ $-xleq -cleq -a.$ Тогда $cnotin X$ и віполняется неравенство $aleq cleq x.$ Следовательно, $aneq inf X.$ Получили противоречие. Таким образом, $$-a=sup(-X)Rightarrow sup(-X)=-inf X.$$
Аналогично доказывается, что $inf (-X)=-sup X.$
Что и требовалось доказать.
Домашнее задание.
1.75. Для множества $X=[-1, , 1]$ найти $max X, ,, min X,$ $sup X$ и $inf X$ если они существуют.
Ответ: $1,, -1,, 1,, -1.$
1.76. Для множества $X=left{xin Z|,, -5leq x <0right}$ найти $max X, ,, min X,$ $sup X$ и $inf X$ если они существуют.
Ответ: Не существует, $-5,, 0,, -5.$
1.81. Пусть $X,,, Ysubset R -$ произвольные ограниченные сверху множества. Доказать, что множество $X+Y={zin R|,, z=x+y,|,, xin X,, yin Y}$ ограничено сверху и справедливы равенства $$sup (X+Y)=sup X+sup Y.$$
Определения
| Определение: |
| Если , то A называется ограниченным сверху множеством.
называется верхней границей множества А. Если , то A называется ограниченным снизу множеством. называется нижней границей множества А. Если , то A называется ограниченным множеством. |
| Определение: |
| Если — ограничено сверху, то наимешьшая из его верхних границ называется верхней гранью. («супремум») |
| Определение: |
| Если — ограничено снизу, то наибольшая из его нижних границ называется нижней гранью. («инфимум») |
Существование грани множества
| Теорема: |
|
Если А ограничено сверху, то у него существует верхняя грань (аналогично для А, ограниченного снизу). |
| Доказательство: |
|
Пусть M — множество верхних границ А. Так как А ограничено сверху, то . По аксиоме непрерывности: :
Получили, что d — верхняя граница А, и d не больше всех верхних границ А . Аналогично для нижней грани ограниченного снизу множества А. |
Принцип вложенных отрезков
| Определение: |
| Множество называется интервалом или открытым промежутком.
Множество называется отрезком или замкнутым промежутком. Обозначение (промежуток) используется, когда неизвестно включение границ. По аналогии определяются и промежутки типа . |
| Определение: |
| Пусть дана система отрезков:
Тогда эта система отрезков называется вложенной. |
| Утверждение: |
|
Определим следующие числовые множества: Пусть . и существуют. В силу вложенности отрезков: |
Исходя из определения граней, если:
