В этом уроке мы поговорим о том как вычислять НОД и НОК. Дело в том, что элементарные арифметические вычисления должен уметь делать любой программист, так как алгоритм вычисления можно встретить во многих программах. Тем более вы их уже должны знать, если вы учились в школе 5 классе.
Наибольший общий делитель. НОД.
Для нахождения общего делителя вам нужно знать следующее:
Запомните: наибольший общий делитель (НОД) двух целых чисел – это наибольшее целое число, на которое делятся оба исходных числа без остатка. Однако одно из исходных чисел должно быть большее нуля.
Запомните: если у вас одно из двух чисел ноль, то НОД будет, то число что больше ноля.
Запомните: существует понятие взаимно-простых чисел, у которого нет общих делителей, кроме единицы. К примеру число 5 и 4, НОД этих чисел будет равен 1, так как если 5 разделить на 4 вы не получите целое число без остатка, следовательно НОД=1
Все остальные числа, у которых НОД больше 1, вычисляются по принципу бинарного алгоритма или с помощью алгоритма Евклида. В этой статье мы подробно разберем алгоритм Евклида, который еще называют взаимным вычитанием, поскольку НОД получается при последовательном вычитании меньшего из большего. Используем алгоритм Евклида в нашем примере НОД(12, 30). По алгоритму Евклида нам надо вычесть из большее меньшее, то есть из 30-12-12=6 В числе 30 у нас может поместиться число 12 только два раза, число 12 называют кратным, и остатком останется число 6. Теперь нам надо из числа 30 отнять кратное числа 6, которое у нас получилось, 30-6-6-6-6-6=5 НОД числа 12 и 30 будет равен 6. Так как нам надо найти именно наибольший делитель в нашем случаи 6 больше 5, следовательно НОД(12,30)=6. Как видите ничего сложного, теперь давайте составим блок схему.
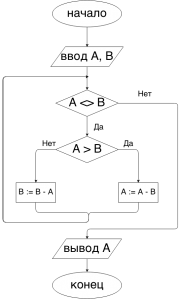
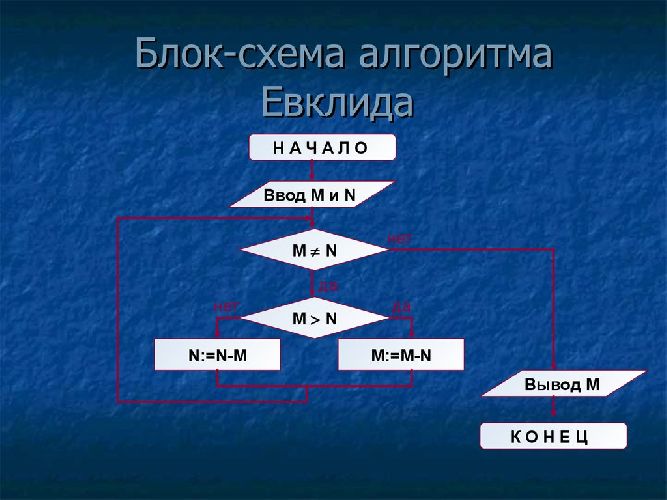
Блок-схема «Алгоритм Евклида»
рис.1
Если число a и b равно, НОД этих чисел будет любое из них, так как они могут делиться друг на друга. Если a и b не равны, мы их сравниваем a<b, если a меньше чем b то их надо поменять местами в a присвоить значение b, в b присвоить значение а и перейти к следующему вычислению описанного ниже. Если a больше чем b то, надо из а вычесть b, результат сохранить в a, и так до тех пор, пока а не станет равно b. Рассмотрим на примере.
Пример НОД(12,30).
- 12=30 | a==b; //в нашем случаи 12 не равно 30
- 12<30 | a<b;//производим сравнение на < >
- 30 12 | a==b; b==a; //меняем местами
- 30-12=18 | a=a-b;//производим вычитание
- 18=12| a==b;//равно ли а и b
- 18<12| a<b; //в нашем случае а >b
- 18-12=6|a=a-b; //производим вычитание
- 6=12|a==b; //в нашем случаи 6 не равно 12
- 6<12|a<b; //производим сравнение на < >
- 6 12| a==b; b==a; //меняем местами
- 12-6=6|a=a-b;//производим вычитание
- 6=6| a==b; //в нашем случаи 6 равно 6
- НОД(12,30)=6;
Наименьшее общее кратное(НОК).
НОК-это число которое из двух и более натуральных чисел является наименьшим натуральным числом, которое само делится нацело, и каждое из исходных чисел.
Самый простой и быстрый способ в плане реализации программного кода, это первоначально вычислить НОД двух чисел, затем произведение исходных двух целых чисел a и b разделить на НОД. Посмотрим на примере как это выглядет. Возьмем за пример все те же цифры 12 и 30 как мы помним наибольшее общее кратное равнялось 6. НОД=6 Следовательно по формуле НОК=a*b/НОД. НОК=12*30/6=60 Есть и другие варианты вычисления НОК к примеру каноническое разложение чисел. Рассмотрим пример, первоначально нам надо выяснить какое из чисел больше, потом мы раскладываем числа на кратные 12=2*2*3 , и число 30=2*3*5 Вычисляем произведение кратных чисел из числа 30, так как оно является наибольшим. В следующей операции, одинаковые цифры вычеркиваются, как это сделал я из большего меньшее, а оставшиеся кратные числа из 12 умножаются друг на друга, у нас осталось только число 2, которое умножается на произведение кратных чисел из 30, в результате вычисления вы и получите НОК. Выглядет это следующим образом НОК=2*3*5*2=60 Хорошо это можно представить в виде столбиков, как это можно видеть из рис. 2.

В целом ничего сложного, главное не запутаться, сейчас мы нарисуем блок схему наименьшего общего кратного (НОК).
Блок схема Наименьшего общего кратного (НОК)
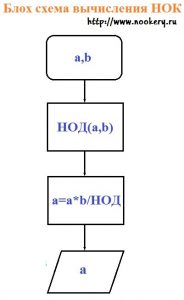
Алгоритм работы программы описан вначале, статьи о НОК.
Но как же быть если нам надо к примеру найти НОД трех и более натуральных чисел, или найти НОК трех или более натуральных чисел. Тут ничего сложного инструкцию по нахождению НОД из 3 чисел и НОК смотрим ниже.
НОД трех чисел:
- Сравниваем все числа К примеру a<b<c
- Начинаем вычисления с больших чисел к меньшим
- Вычисляем НОД по аналогии с двумя числами a и b
- Вычисляем по аналогии чисел НОД(a,b) и с Пример: НОД(a,b,c)=НОД((НОД(a,b)),с);
- НОД(12,30,60)
- 12<30<60
- НОД(60,30)=30
- НОД(30,12)=6
Точно так же производиться вычисления НОД из четырех чисел из пяти итд. По аналогии с НОД вычисляется и НОК с тремя и более числами. Приведу в пример НОД трех чисел блок схему алгоритма смотрите рис. 4.
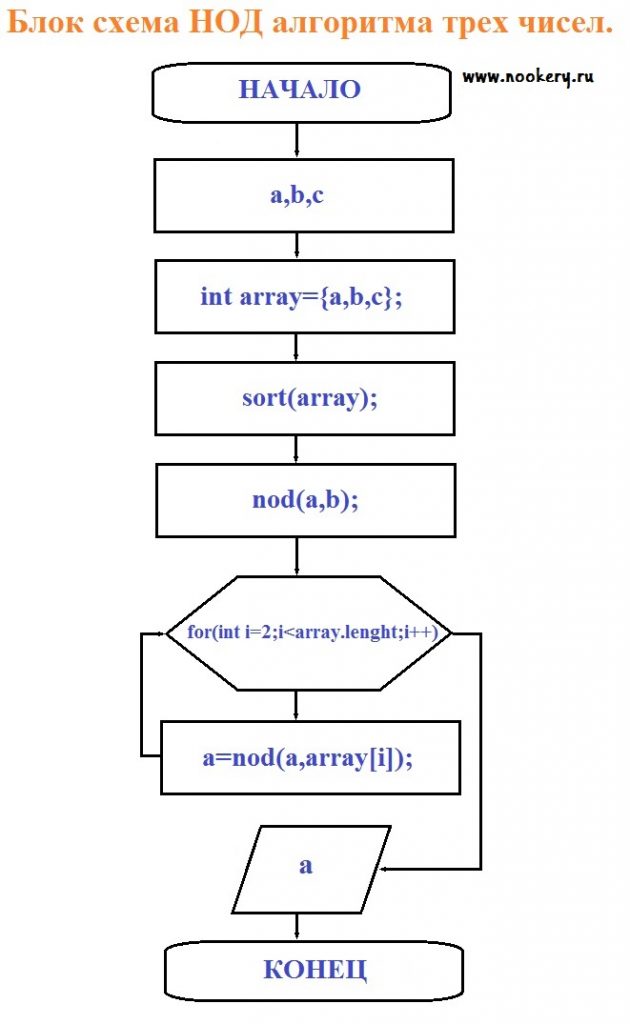
Блок схема НОД алгоритма трех чисел, четырех чисел итд.
рис. 4
Разберем по подробнее работу программы блок схемы из рис. 4.
- У нас подается 3 числа, но их может быть сколько угодно.
- Их мы записываем в массив array.
- Выполняем метод sort(); Это мой метод он принимает массив чисел, делает сортировку по убыванию, пузырьковым методом, о нем вы можете прочитать из уроков о массивах.
- Выполняем метод nod(), который принимает первые два числа. Я создал метод по аналогии как написано выше в этой статье.
- В следующем блоке я помещаю в тело цикла метод nod(), который присваиваю возвращаемое число из метода nod() переменной a.
- Выводим результат.
- Завершаем работу программы.
Скачать калькулятор НОК и НОД .
Пока писал статью, написал программу НОК и НОД вычисления, которую можете скачать с сайта. Работа программы очень простая, достаточно в текстовое поле вписать цифры через пробел или запятую, нажать на кнопку вычислить или Enter и программа выведет результат. Программа написана на языке java. Может запускаться со всех систем.
рис 5.
Скачать калькулятор НОК и НОД .
Алгоритм Евклида — нахождение наибольшего общего делителя
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Решение задачи на языке программирования Python
Алгоритм нахождения НОД делением
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
a = int(input()) b = int(input()) while a != 0 and b != 0: if a > b: a = a % b else: b = b % a print(a + b)
В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для определения НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.
Если условием завершения цикла является равенство хотя бы одной из переменных нулю (a == 0 or b == 0), то условием продолжения его работы является обратное этому условие — обе переменные должны иметь отличные от нуля значения (a != 0 and b != 0).
Для того, чтобы вышеприведенная программа могла обрабатывать отрицательные числа, в логическом выражении при if должны сравниваться модули значений переменных: if abs(a) > abs(b):. Иначе большим числом может оказаться меньшее по модулю. В этом случае интерпретатор Питона в качестве остатка от деления выдает вещественное число. В результате это приводит к зацикливанию, так как низвести переменные до нуля становится как минимум маловероятным.
Алгоритм нахождения НОД вычитанием
- Из большего числа вычитаем меньшее.
- Если получается 0, значит, числа равны друг другу и являются НОД (следует выйти из цикла).
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6
a = int(input()) b = int(input()) while a != b: if a > b: a = a - b else: b = b - a print(a)
Функция, вычисляющая НОД
def gcd(m, n): while m != n: if m > n: m = m - n else: n = n - m return n a = int(input()) b = int(input()) print(gcd(a, b))
Функция gcd модуля math
В модуле math языка программирования Python есть функция gcd, вычисляющая наибольший общий делитель двух чисел.
>>> import math >>> math.gcd(30, 18) 6
Больше задач в PDF
Алгоритм Евклида

4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
Для иллюстрации основных алгоритмических конструкций в информатике и программировании часто применяют алгоритм Евклида. Применяя этот алгоритм, находят наибольший общий делитель двух целых чисел. Благодаря своей простоте и наглядности этот алгоритм не теряет популярности и по сей день.
Что такое алгоритм Евклида
В математике известен конструктивный алгоритм определения наибольшего общего делителя двух целых чисел, который носит название алгоритма Евклида. Греческий ученый математик Евклид первым описал этот алгоритм в своем научном трактате «Начала».
Евклид жил в третьем веке до нашей эры в древней Греции. Он первым написал трактат по математике, в котором изложил основы планиметрии, стереометрии и теории чисел.
Для понимания сути алгоритма вычисления НОД удобна его геометрическая трактовка.
Рассматриваются два отрезка разной длины. Из большего отрезка вычитают меньший, и затем больший отрезок заменяют результатом проведенного вычитания. Это действие выполняют несколько раз, пока отрезки не станут одинаковой длины. Полученная величина отрезков и есть наибольший общий делитель.
Этапы алгоритма Евклида
Процесс вычисления наибольшего общего делителя двух чисел удобно представить в виде цепочки шагов.
Построчная запись алгоритма Евклида
- Определиться со значением первого числа X.
- Определиться со значением второго числа Y.
- Если X≠Y, то выполнять пункт 4, иначе перейти к пункту 5.
- Если X>Y, то заменить X на X-Y и перейти к пункту 3, иначе заменить Y на Y- X и перейти к пункту 3.
- Считать Х наименьшим общим делителем.
В рассмотренной последовательности используются условные конструкции и конструкция повтора.
Для наглядного представления алгоритма Евклида используется блок-схема.
Запись алгоритма Евклида на языке Паскаль
При записи алгоритма Евклида на процедурном языке программирования Паскаль необходимо строго придерживаться структуры программы. Начинать программу необходимо с заголовка, записывая ключевое слово PROGRAM и название программы. Пусть программа называется EVKLID. В конце первой строки ставится точка с запятой. Этот знак следует ставить в конце каждой строки программы, а точнее после каждого оператора, процедуры или функции. Отсутствие его приведет к ошибке при отладке программы.
При записи алгоритма на языке программирования следует помнить правила использования ключевых слов, всегда описывать предварительно используемые переменные и не допускать синтаксических ошибок.
Описание переменных
В алгоритме используется всего две переменные X и Y, которые следует описать в разделе описания переменных, задавая им целый тип.
Var X, Y : integer;
Основная часть программы, в которой производятся все вычисления, заключается в операторные скобки begin и end. В конце программы обязательно ставится точка.
Ввод переменных с клавиатуры
Значения переменных X и Y удобнее всего вводить с клавиатуры, используя процедуры ввода чисел с клавиатуры READLN. Перед вводом данных лучше вывести пользователю будущей программы сообщение «Введите число» с использованием процедуры вывода WRITELN.
Часть программы, предназначенная для ввода чисел, может выглядеть так:
write(‘Введите первое число X = ‘);
readln(X);
write(‘Введите второе число Y = ‘);
readln(Y);
Организация повтора
Операцию вычитания в соответствии с алгоритмом следует выполнять до тех пор, пока выполняется условие неравности переменных X и Y. При равенстве X и Y повтор следует прекратить. Искомое число найдено.
Для реализации цикла, в котором итерации выполняются в соответствии с условием, удобнее всего использовать оператор с предусловием WHILE..DO. В решаемой задаче эта часть программы будет выглядеть так:
while X <> Y do
Запись условной конструкции на языке Паскаль
Условие на языке Паскаль записывается с помощью оператора IF..THEN..ELSE.
if X > Y then X:= X – Y else Y:= Y – X;
И в завершении программы, искомый результат выводится на экран.
Writeln (‘НОД чисел X и Y равен ‘, X);
Весь текст программы будет иметь вид:
program evklid;
Var X, Y : integer;
write(‘Начните вводить первое число X = ‘);
readln(X);
write(‘Начните вводить второе число Y = ‘);
readln(Y);
while X <> Y do
if X > Y then X:= X – Y else Y:= Y – X;
Writeln (‘НОД чисел X и Y равен ‘, X);
End.
Что мы узнали?
Для расчета наибольшего общего делителя двух целых чисел уже более тысячи лет используется простой и наглядный алгоритм, придуманный древнегреческим ученым Евклидом. Он хорошо иллюстрирует работу условных и циклических операторов в языке Паскаль.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Александр Осышный
5/5
-
Grimlok The-Fox
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
А какая ваша оценка?
Содержание
- Алгоритм евклида в виде блок схемы
- Идея алгоритма Евклида
- Описание алгоритма Евклида блок-схемой
- Программа на АЯ и на Паскале
- Алгоритм Евклида — нахождение наибольшего общего делителя
- Алгоритм нахождения НОД делением
- Алгоритм нахождения НОД вычитанием
- Функция вычисления НОД
- Блок-схема алгоритма Евклида
- Наибольший общий делитель и наименьшее общее кратное.
- Наибольший общий делитель. НОД.
- Блок-схема «Алгоритм Евклида»
- Наименьшее общее кратное(НОК).
- Блок схема Наименьшего общего кратного (НОК)
- Скачать калькулятор НОК и НОД .
- Уроки 46 — 47 Сочетание циклов и ветвлений. Алгоритм Евклида (§ 16. Алгоритм Евклида) Использование алгоритма Евклида при решении задач
- Содержание урока
- Алгоритм Евклида
- Наибольший общий делитель
- Идея алгоритма Евклида
- Описание алгоритма Евклида блок-схемой
- Коротко о главном
- Вопросы и задания
Алгоритм евклида в виде блок схемы
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если M>N, то
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М — N = К(m — n), откуда следует, что К — делитель числа М — N. Значит, все общие делители чисел М и N являются делителями их разности М — N, в том числе и наибольший общий делитель.
Второе очевидное свойство:
Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) заменить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) =НОД(8, 
Описание алгоритма Евклида блок-схемой
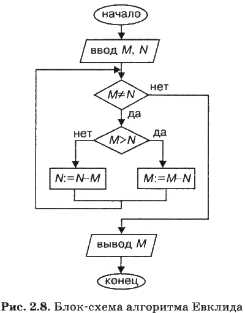
На рис. 3.12 приведена блок-схема алгоритма Евклида.
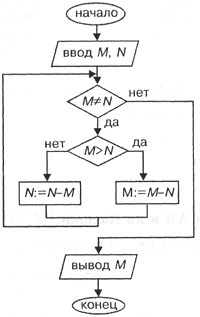 |
| Рис. 3.12. Блок-схема алгоритма Евклида |
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
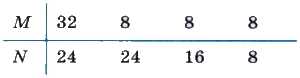
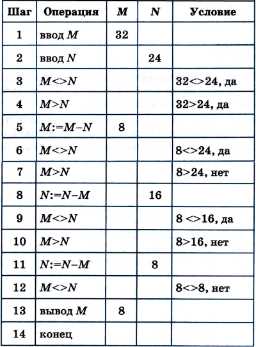
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.
| Шаг | Операция | M | N | Условие |
| 1 | ввод М | 32 | ||
| 2 | ввод N | 24 | ||
| 3 | M ¹ N | 32 ¹ 24, да | ||
| 4 | M>N | 32>24, да | ||
| 5 | M:=M-N | 8 | ||
| 6 | M ¹ N | 8 ¹ 24, да | ||
| 7 | M>N | 8>24, нет | ||
| 8 | N:=N-M | 16 | ||
| 9 | M ¹ N | 8 ¹ 16, да | ||
| 10 | M>N | 8>16, нет | ||
| 11 | N:=N-M | 8 | ||
| 12 | M ¹ N | 8 ¹ 8, нет | ||
| 13 | вывод M | 8 | ||
| 14 | конец |
В итоге получился верный результат.
Программа на АЯ и на Паскале
Запишем алгоритм на АЯ и программу на Паскале.
| алг Евклид цел М, N нач вывод » Введите М и N» ввод М, N пока М N, повторять нц если M>N то M:=M-N иначе N:=N-M кв кц вывод «НОД=»,М кон |
Program Evklid; var M, N: integer; begin writeln(‘Введите М и N’); readln(M, N); while M<>N do begin if M>N then M:=M-N else N:=N-M end; write(‘Н0Д=’,М) end. |
1. Выполните на компьютере программу Evklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
Источник
Алгоритм Евклида — нахождение наибольшего общего делителя
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Алгоритм нахождения НОД делением
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.
Алгоритм нахождения НОД вычитанием
- Из большего числа вычитаем меньшее.
- Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6
Функция вычисления НОД
Блок-схема алгоритма Евклида
Примечание. В модуле math языка программирования Python есть функция gcd(), вычисляющая наибольший общий делитель двух чисел.
Источник
Наибольший общий делитель и наименьшее общее кратное.
В этом уроке мы поговорим о том как вычислять НОД и НОК. Дело в том, что элементарные арифметические вычисления должен уметь делать любой программист, так как алгоритм вычисления можно встретить во многих программах. Тем более вы их уже должны знать, если вы учились в школе 5 классе.
Наибольший общий делитель. НОД.
Для нахождения общего делителя вам нужно знать следующее:
Запомните: наибольший общий делитель (НОД) двух целых чисел – это наибольшее целое число, на которое делятся оба исходных числа без остатка. Однако одно из исходных чисел должно быть большее нуля.
Запомните: если у вас одно из двух чисел ноль, то НОД будет, то число что больше ноля.
Запомните: существует понятие взаимно-простых чисел, у которого нет общих делителей, кроме единицы. К примеру число 5 и 4, НОД этих чисел будет равен 1, так как если 5 разделить на 4 вы не получите целое число без остатка, следовательно НОД=1
Все остальные числа, у которых НОД больше 1, вычисляются по принципу бинарного алгоритма или с помощью алгоритма Евклида. В этой статье мы подробно разберем алгоритм Евклида, который еще называют взаимным вычитанием, поскольку НОД получается при последовательном вычитании меньшего из большего. Используем алгоритм Евклида в нашем примере НОД(12, 30). По алгоритму Евклида нам надо вычесть из большее меньшее, то есть из 30-12-12=6 В числе 30 у нас может поместиться число 12 только два раза, число 12 называют кратным, и остатком останется число 6. Теперь нам надо из числа 30 отнять кратное числа 6, которое у нас получилось, 30-6-6-6-6-6=5 НОД числа 12 и 30 будет равен 6. Так как нам надо найти именно наибольший делитель в нашем случаи 6 больше 5, следовательно НОД(12,30)=6. Как видите ничего сложного, теперь давайте составим блок схему.
Блок-схема «Алгоритм Евклида»
Если число a и b равно, НОД этих чисел будет любое из них, так как они могут делиться друг на друга. Если a и b не равны, мы их сравниваем a
Наименьшее общее кратное(НОК).
В целом ничего сложного, главное не запутаться, сейчас мы нарисуем блок схему наименьшего общего кратного (НОК).
Блок схема Наименьшего общего кратного (НОК)

Алгоритм работы программы описан вначале, статьи о НОК.
Но как же быть если нам надо к примеру найти НОД трех и более натуральных чисел, или найти НОК трех или более натуральных чисел. Тут ничего сложного инструкцию по нахождению НОД из 3 чисел и НОК смотрим ниже.
- Сравниваем все числа К примеру a Блок схема НОД алгоритма трех чисел, четырех чисел итд.
Разберем по подробнее работу программы блок схемы из рис. 4.
- У нас подается 3 числа, но их может быть сколько угодно.
- Их мы записываем в массив array.
- Выполняем метод sort(); Это мой метод он принимает массив чисел, делает сортировку по убыванию, пузырьковым методом, о нем вы можете прочитать из уроков о массивах.
- Выполняем метод nod(), который принимает первые два числа. Я создал метод по аналогии как написано выше в этой статье.
- В следующем блоке я помещаю в тело цикла метод nod(), который присваиваю возвращаемое число из метода nod() переменной a.
- Выводим результат.
- Завершаем работу программы.
Скачать калькулятор НОК и НОД .
Пока писал статью, написал программу НОК и НОД вычисления, которую можете скачать с сайта. Работа программы очень простая, достаточно в текстовое поле вписать цифры через пробел или запятую, нажать на кнопку вычислить или Enter и программа выведет результат. Программа написана на языке java. Может запускаться со всех систем.
Скачать калькулятор НОК и НОД .
Источник
Уроки 46 — 47
Сочетание циклов и ветвлений. Алгоритм Евклида
(§ 16. Алгоритм Евклида)
Использование алгоритма Евклида при решении задач
Содержание урока
Алгоритм Евклида
Алгоритм Евклида
 |
 |
|
|
|
 |
 |
Наибольший общий делительРассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел. Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они оба делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так: НОД(12, 18) = 6. Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом: В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида. Идея алгоритма ЕвклидаИдея этого алгоритма основана на том свойстве, что если M > N, то Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа. Легко доказать это свойство. Пусть К — общий делитель М и N (М > N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М — N = К(m — n), откуда следует, что К — делитель числа М — N. Значит, все общие делители чисел М и N являются делителями их разности М — N, в том числе и наибольший общий делитель. Второе очевидное свойство: Для «ручного» счета алгоритм Евклида выглядит так: 1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма; 2) заменить большее число разностью большего и меньшего из чисел; 3) вернуться к выполнению п. 1. Рассмотрим этот алгоритм на примере М=32, N=24: Получили: НОД(32, 24) = НОД(8, Описание алгоритма Евклида блок-схемойНа рисунке 2.8 приведена блок-схема алгоритма Евклида. Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность. А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24: В итоге получился верный результат. Коротко о главномАлгоритм Евклида предназначен для получения наибольшего общего делителя двух натуральных чисел. Структура алгоритма Евклида — цикл с вложенным ветвлением. Ручная трассировка может использоваться для проверки правильности лишь сравнительно простых алгоритмов. Поиск алгоритмических ошибок в программе производится с помощью тестирования. Вопросы и задания1. Выполните на компьютере программу Evklid (из параграфа). Протестируйте ее на значениях М = 32, N = 24; М = 696, N = 234. 2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу: 3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу: Следующая страница Источник Adblock |
Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.
Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.
Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.
Переборный алгоритм
Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.
var
a, b, d: integer;
begin
write('Введите два числа: ');
readln(a, b);
if a < b then d := a + 1 else d := b + 1;
{так как мы используем цикл с постусловием,
необходимо минимальное значение увеличить на один,
иначе цикл repeat, в силу своих конструктивных особенностей,
не учтет это минимальное число
и не сделает его кандидатом в НОД. Например, 5 и 25.}
repeat d := d - 1
until (a mod d = 0) and (b mod d = 0);
write('NOD = ', d)
end.
Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.
Алгоритм Евклида «с вычитанием»
Пусть a и b — целые числа, тогда верны следующие утверждения:
- Все общие делители пары a и b являются также общими делителями пары a — b, b;
- И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
- НОД(A, B) = НОД(A — B, B), если A > B;
- НОД(A, 0) = A.
Доказательство:
- Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
- Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
- Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
- Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.
Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.
Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.
Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.
На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.
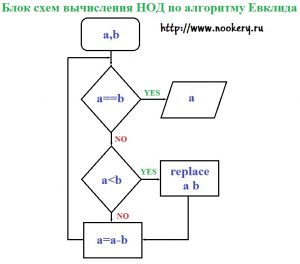
Блок — схема алгоритма Евклида «с вычитанием»
Программа
var
a, b: integer;
begin
write('a = ');
readln(a);
write('b = ');
readln(b);
while a <> b do
if a > b then
a := a - b
else
b := b - a;
writeln('NOD = ', a);
end.
Алгоритм Евклида с «делением»
Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).
Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.
Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.
var
a, b: integer;
begin
write('a = ');
readln(a);
write('b = ');
readln(b);
while (a <> 0) and (b <> 0) do
if a >= b
then
a := a mod b
else
b := b mod a;
write(a + b)
end.
На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.




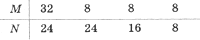



 Дополнительный материал к главе II (§§ 8 — 21). Сложность алгоритмов
Дополнительный материал к главе II (§§ 8 — 21). Сложность алгоритмов