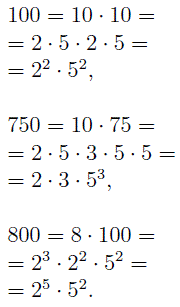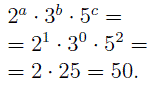Пример:
имеются (45) апельсинов и (60) мандаринов. Найди наибольшее количество одинаковых наборов, которые можно собрать из этих фруктов.
Решая такую задачу, найдём все делители числа (45) и числа (60).
Для (45) это: (1); (3); (5); (9); (15); (45).
Для (60) это: (1); (2); (3); (4); (5); (6); (10); (12); (15); (20); (30), (60).
Общими делителями этих чисел будут: (1); (3); (5); (15).
Наибольшим является число (15).
Наибольшее натуральное число, на которое делятся без остатка числа (m) и (n), называют наибольшим общим делителем этих чисел.
Обозначают: (НОД(m; n)).
Так, в задаче (НОД(45; 60) = 15).
Наибольший общий делитель нескольких натуральных чисел можно найти, не выписывая все делители этих чисел.
Правило отыскания (НОД):
1. разложить данные числа на простые множители.
2. Выписать все простые числа, которые одновременно входят в каждое из полученных разложений.
3. Каждое из выписанных простых чисел взять с наименьшим из показателей степени, с которыми оно входит в разложения данных чисел.
4. Записать произведение полученных степеней.
48=2⋅2⋅2⋅2⋅3=24⋅3;36=2⋅2⋅3⋅3=22⋅32;НОД(48;36)=22⋅3=12.
Пример:
найдём (НОД(20; 27)).
Разложив на множители каждое из этих чисел, получим:
20=2⋅2⋅5=22⋅5;27=3⋅3⋅3=33.
Значит, у данных чисел нет других общих множителей, кроме (1), т. е. число (1) — единственный общий делитель данных чисел.
(НОД(20; 27) = 1).
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен
(1).
Числа (20) и (27) — взаимно простые.
Признак делимости на произведение взаимно простых чисел:
если число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.
Пример:
число (540) делится как на (20), так и на (27). Значит, (540) будет делиться и на их произведение, т. е.
540:(20⋅27)=540:540=1
.
Сейчас мы научимся определять наибольший общий делитель для двух или трех чисел, познакомимся с алгоритмом Евклида и узнаем много всего интересного.
Эта информация доступна зарегистрированным пользователям
Самое большое натуральное число, на которое делятся нацело два или более чисел, называется их наибольшим общим делителем (НОД).
При поиске НОД, например, 36 и 24, надо:
1. Записать их в виде разложения на простые множители
$$mathbf{36 = 2cdot2cdot3cdot3}$$
$$mathbf{24 = 2cdot2cdot2cdot3}$$
2. Среди множителей (mathbf{2cdot2cdot3cdot3}) и (mathbf{2cdot2cdot2cdot3}), которые входят в разложения этих чисел, нужно оставить только одинаковые множители — это (mathbf{2cdot2cdot3})
3. Вычислить произведение множителей, которые остались: (mathbf{2cdot2cdot3 = 12})
В итоге НОД чисел 36 и 24 равен 12.
Если при нахождении НОДа среди чисел есть одно, на которое делятся все остальные, то оно и будет тем самым НОДом.
Например, у чисел 12, 36 и 48 НОД = 12
Эта информация доступна зарегистрированным пользователям
Пример 1
Найдите все общие делители чисел:
А) 70, 105
Б) 18, 24
В) 45,75
Г) 324, 111, 432
Д) 320, 640, 960
Решение
А)
$$mathbf{70 = 2cdot5cdot7}$$
$$mathbf{105 = 3cdot5cdot7}$$
$$mathbf{НОД (70; 105) = 5cdot7 = 35}$$
Б)
$$mathbf{18 = 2cdot3cdot3}$$
$$mathbf{24 = 2cdot2cdot2cdot3}$$
$$mathbf{НОД (18; 24) = 2cdot3 = 6}$$
В)
$$mathbf{45 = 3cdot3cdot5}$$
$$mathbf{75 = 3cdot5cdot5}$$
$$mathbf{НОД (45; 75) = 3cdot5 = 15}$$
Г)
$$mathbf{324 = 2cdot2cdot3cdot3cdot3cdot3}$$
$$mathbf{111 = 3cdot37}$$
$$mathbf{432 = 2cdot2cdot2cdot2cdot3cdot3cdot3}$$
$$mathbf{НОД (324; 111; 432) = 3}$$
Д)
$$mathbf{320 = 2cdot2cdot2cdot2cdot2cdot2cdot5}$$
$$mathbf{640 = 2cdot2cdot2cdot2cdot2cdot2cdot2cdot5}$$
$$mathbf{960 = 2cdot2cdot2cdot2cdot2cdot2cdot3cdot5}$$
$$mathbf{НОД (320; 640; 960) = 2cdot2cdot2cdot2cdot2cdot2cdot5 = 320}$$
Пример 2
На новогоднем утреннике дети получили пакеты с подарками. Всего во всех пакетах находилось 159 апельсинов и 106 яблок. Сколько детей было на новогодней ёлке? Сколько в каждом пакете было яблок и сколько апельсинов?
Решение
$$mathbf{159 = 3cdot53}$$
$$mathbf{106 = 2cdot53}$$
$$mathbf{НОД (159; 106) = 53}$$
Ребят на елке было 53 человека. В каждом пакете подарка было по 3 апельсина и 2 яблока.
Пример 3
Для выезда на природу работникам предоставили несколько автобусов. В каждом автобусе равное число мест для сидения. 184 человека выехали в лес, а 138 отправились на озеро. Так вышло, что все места в автобусах были заняты, и, стоя, никто не ехал. Сколько автобусов было и сколько пассажиров ехало в каждом из них?
Решение
$$mathbf{184 = 2cdot2cdot2cdot23}$$
$$mathbf{138 = 2cdot3cdot23}$$
$$mathbf{НОД (184; 138) = 46}$$
В каждом автобусе было по 46 мест. В лес поехало 4 автобусов, а на озеро поехало 3 автобусов. Всего было 4 + 3 = 7 автобусов.
Эта информация доступна зарегистрированным пользователям
Давайте разберёмся с некоторыми натуральными числами.
Число 15 имеет делители 1, 3, 5, а число 16 имеет делители 1, 2, 4, 8
У этих чисел единственный одинаковый делитель — это число 1 , поэтому они будут называться взаимно простыми.
Рассмотрев этот и другие примеры, не сложно догадаться, что натуральные числа, у которых НОД равен 1, называются взаимно простые.
Пример 1
Возьмем две пары чисел 12 и 18, 13 и 21. Выясним, есть ли среди них взаимно простые числа. Для этого каждое из чисел распишем по простым делителям.
12 имеет делители 1, 2, 3, 4, 6, 12
18 имеет делители 1, 2, 3, 6, 9, 18
Значит, числа 12 и 18 кроме единицы имеют общие делители 2, 3, 6, поэтому они не являются взаимно простыми числами. Повторим действия с другой парой чисел 13 и 21.
Число 13 делится нацело на 1, 13, а число 21 делится нацело на 1, 3, 7, 21.
Тут уже ситуация другая. 13 и 21 имеют единственный общий делитель — 1.
Значит, вторая пара чисел состоит из взаимно простых.
Пример 2
Пусть у нас есть два числа 45 и 32, которые являются натуральными и составными.
Первое из них 45 имеет делители 1, 3, 5, 9, 15, 45, а натуральное число 32 имеет делители 1, 2, 4, 8, 16, 32
Оба числа из этой пары имеют единственный общий делитель- 1
Значит, числа 45 и 32 являются взаимно простыми. Запишем оба числа в виде разложения на простые множители
$$mathbf{45 = 3cdot3cdot5}$$
$$mathbf{32 = 2cdot2cdot2cdot2cdot2}$$
Числа из нашего примера, 45 и 32, в записи на множители не содержат равных чисел. Значит, разложения на простые множители двух и более взаимно простых чисел не включают одинаковых простых множителей.
Пример 3
Являются ли взаимно простыми числа:
А) 55 и 40
Б) 77 и 92
В) 14, 32 и 41
Г) 231 и 298
Д) 68 и 137
Решение:
А)
$$mathbf{55 = 5cdot11}$$
$$mathbf{40 = 2cdot2cdot2cdot5}$$
$$mathbf{НОД (55; 40) = 5}$$
Нет, не являются взаимно простыми числами
Б)
$$mathbf{77 = 7cdot11}$$
$$mathbf{92 = 2cdot2cdot23}$$
$$mathbf{НОД (77; 92) = 1}$$
Да, являются взаимно простыми числами
В)
$$mathbf{14 = 2cdot7}$$
$$mathbf{32 = 2cdot2cdot2cdot2cdot2}$$
$$mathbf{41 — простое:число}$$
$$mathbf{НОД (14; 32; 41) = 1}$$
Да, являются взаимно простыми числами
Г)
$$mathbf{231 = 3cdot7cdot11}$$
$$mathbf{298 = 2cdot149}$$
$$mathbf{НОД (231; 298) = 1}$$
Да, являются взаимно простыми числами
Д)
$$mathbf{68 = 2cdot2cdot17}$$
$$mathbf{137- простое}$$
$$mathbf{НОД (68; 137) = 1}$$
Да, являются взаимно простыми числами
Пример 4
Найдите разложение на простые множители наибольшего общего делителя чисел a и b, если:
А) (mathbf{a = 2cdot3cdot5cdot2cdot3}) и (mathbf{b = 2cdot2cdot5cdot7})
Б) (mathbf{a = 3cdot5cdot5cdot7cdot17}) и (mathbf{b = 5cdot3cdot3cdot17})
Решение
А) (mathbf{НОД (a; b) = НОД (2cdot3cdot5cdot2cdot3; 2cdot2cdot5cdot7) = 2cdot2cdot5 = 20})
Б) (mathbf{НОД (a; b) = НОД (3cdot5cdot5cdot7cdot17; 5cdot3cdot3cdot17) = 5cdot3cdot17 = 255})
Признак делимости на произведение взаимно простых чисел: если данное натуральное число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.
Рассмотрим этот признак на примере трех взаимно простых чисел.
Возьмем, например, 420.
Число 420 без остатка делится на 2, на 5 и на 7.
Числа 2, 5, 7 являются взаимно простыми (так как их НОД равен 1). Проверим, будет ли делиться 420 на произведение взаимно простых чисел 2, 5 и 7.
(mathbf{2cdot5cdot7 = 70})
(mathbf{frac{420}{70} = 6})
Очевидно, что 420 делится нацело на произведение чисел двух, пяти и семи.
Правило можно применять для любого количества множителей.
Эта информация доступна зарегистрированным пользователям
Алгоритм Евклида, который используется для нахождения НОДа и с которым мы познакомились выше, широко применяется при решении других математических задач. Например, он связан с цепными дробями и позволяет с их помощью уменьшать большие дроби до маленьких.
$$frac{105}{38} = 2+frac{1}{1+frac{1}{3+frac{1}{4+frac{1}{2}}}}$$
Кроме того, алгоритм используется при решении линейных диофантовых уравнений. Это такие уравнения, у которых могут быть несколько неизвестных целых величин, и все их нужно найти. Например, может быть такое уравнение:
$$mathbf{2x+3y = 1}$$
Решением этого уравнения будет пара чисел
$$mathbf{x = 5}$$ и $$mathbf{y = -3}$$
Могут быть и другие пары решений. Решение таких уравнений начинается обычно с нахождения НОДа чисел, стоящих перед неизвестными. В нашем случае мы бы находили (mathbf{НОД(2, 3)})
Не всегда данный алгоритм позволяет быстро решать задачи. Иногда можно потратить много времени, сделать много вычислений, прежде чем найти нужный результат. Это единственный большой минус одного из старейших численных алгоритмов.
Наибольший общий делитель. Взаимно простые числа
Содержание
Общий делитель нескольких натуральных чисел. Наибольший общий делитель. Взаимно простые числа
ОПРЕДЕЛЕНИЕ 1. Общим делителем нескольких натуральных чисел называют число, которое является делителем каждого из этих чисел.
ОПРЕДЕЛЕНИЕ 2. Самый большой из общих делителей называют наибольшим общим делителем (НОД).
ПРИМЕР 1. Общими делителями чисел 30 , 45 и 60 будут числа 1 , 3 , 5 , 15 . Наибольшим общим делителем этих чисел будет
НОД ( 30 , 45 , 10) = 15 .
ОПРЕДЕЛЕНИЕ 3. Если наибольший общий делитель нескольких чисел равен 1 , то эти числа называют взаимно простыми.
ПРИМЕР 2. Числа 40 и 3 будут взаимно простыми числами, а числа 56 и 21 не являются взаимно простыми, поскольку у чисел 56 и 21 есть общий делитель 7 , который больше, чем 1.
ЗАМЕЧАНИЕ. Если числитель дроби и знаменатель дроби являются взаимно простыми числами, то такая дробь несократима.
Алгоритм нахождения наибольшего общего делителя
Рассмотрим алгоритм нахождения наибольшего общего делителя нескольких чисел на следующем примере.
ПРИМЕР 3. Найти наибольший общий делитель чисел 100, 750 и 800 .
РЕШЕНИЕ. Разложим эти числа на простые множители:
Простой множитель 2 в первое разложение на множители входит в степени 2 , во второе разложение – в степени 1 , в третье разложение – в степени 5 . Обозначим наименьшую из этих степеней буквой a . Очевидно, что a = 1 .
Простой множитель 3 в первое разложение на множители входит в степени 0 (другими словами, множитель 3 в первое разложение на множители вообще не входит), во второе разложение входит в степени 1 , в третье разложение – в степени 0 . Обозначим наименьшую из этих степеней буквой b . Очевидно, что b = 0 .
Простой множитель 5 в первое разложение на множители входит в степени 2 , во второе разложение – в степени 3 , в третье разложение – в степени 2 . Обозначим наименьшую из этих степеней буквой c . Очевидно, что c = 2 .
Теперь рассмотрим число:
Это число и есть наибольший общий делитель чисел 100, 750 и 800 .
ОТВЕТ: 50 .
ЗАМЕЧАНИЕ. Чтобы сократить дробь, нужно её числитель и знаменатель разделить на их наибольший общий делитель.
План урока:
Наибольший общий делитель
Взаимно простые числа
Минутка истории
Наибольший общий делитель
Встречаются ситуации, когда хочется понимать, на какое максимальное количество делится одновременно несколько числовых значений.
Например:
В городском парке проводился ежегодный марафон. Для участия в марафоне пришло 36 мальчиков, 24 девочки. По условиям соревнования, всех участников необходимо поделить на команды, в которые войдут и мальчики, и девочки. Сколько одинаковых команд можно сформировать из данного количества детей?
Чтобы ответь на вопрос задачи, вычислим максимальное числовое значение, являющееся делителем для количества всех ребят одновременно.
Выполним необходимые вычисления – определим существующие множители. Вычисления запишем в столбик.
Начнем с 36.
36 | 2
18
Полученное частное – 18, оно четное. Делитель остается прежним:
36 | 2
18 | 2
9
9 – нечетное, поэтому берем следующий делитель – 3:
36 | 2
18 | 2
9 | 3
3
Частное – простое числовое значение, делится само на себя:
36 | 2
18 | 2
9 | 3
3 | 3
1
Частное – единица, разложение окончено.
Выпишем составляющие:
36 = 2×2×3×3
Переходим к 24.
24 заканчивается четной цифрой, значит, кратно двум:
242
12
Делитель оставляем прежним, частное 12 – четное:
242
122
6
Результат деления 6, снова делим на 2:
24 | 2
12 | 2
6 | 2
3
Получили простое числовое значение, которое делится само на себя:
24 | 2
12 | 2
6 | 2
3 | 3
1
Разложение окончено. Запишем полученные компоненты:
24 = 2 × 2 × 2 × 3.
В финале выполненных вычислений мы получили:
36 = 2 × 2 × 2 × 3× 3;
24 = 2 × 2 × 2 × 3.
Давайте выберем одинаковые составляющие. Видно, что в каждом выражении такими составляющими будут: 2 ×2 × 3.
Перемножим выделенные компоненты:
2 ×2 × 3 = 12.
12 – самое большое числовое значение, на которое можно разделить оба делимых.
Мы выяснили, что всех участников можно распределить на 12 одинаковых команд.
Решая задачу, нашли самый большой делитель двух данных чисел. В арифметике число, являющееся самым большим делителем, одновременно для нескольких делимых, называют наибольшим общим делителем.
Для определения наибольшего общего делителя, нужно придерживаться определенного порядка выполнения математических действий:
Выполним задание.
Определите НОД (наибольший общий делитель) 66 и 44.
Чтобы выполнить задание будем придерживаться рассмотренного алгоритма действий.
Определим компоненты, входящие в состав числового значения.
Значит:
66 | 2
33
Результат деления оканчивается нечетной цифрой, проверяем по признакам делимости на 3:
66 | 2
33 | 3
11
Мы получили простое числовое значение
66 | 2
33 | 3
11 | 11
1
В итоге вычислений – 1, разложение окончено.
Переходим ко второму известному значению.
- 1) Определим составляющие, входящие в состав:
Проверяем по признакам делимости. Данное числовое значение заканчивается четной цифрой, значит, оно делится на 2.
44 | 2
22
Частное снова делится на 2:
44 | 2
22 | 2
11
В результате простое число, делим само на себя:
44 | 2
22 | 2
11 | 11
1
Разложение окончено.
- 2) Выпишем компоненты обоих делимых, определим одинаковые:
66 = 2 × 3 × 11
44 = 2 ×2 × 11
- 3) Перемножим выделенные составляющие:
2 × 11=22
Выходит, что наибольший общий делитель – 22.
На письме, рядом с обозначением НОД в скобочках записывают делимые, для которых определяли наибольший общий делитель:
НОД (66;44) = 22.
Разберем задачу
Выпускники на праздник последнего звонка, приготовили цветы своим учителям. Они принесли 69 роз и 46 гладиолусов и разделили поровну между всеми учителями. Сколько учителей поздравили выпускники?
Зная, что цветы были поделены поровну, нам необходимо найти максимальную численность учителей,на которую можно разделить и розы и гладиолусы.
Для определения НОД данных делимых, воспользуемся алгоритмом вычисления:
- 1) Разложим на составляющие:
69 | 3 46 | 2
23 | 23 23 | 23
1 1
- 2) Выберем общее числовое значение находящееся в составляющих :
69 = 3 × 23
46 = 2 × 23.
Нам подходит только 23.
НОД (69;46) = 23.
Наибольшим общим делителем для данных чисел будет 23.
Выпускники поздравили 23 учителя.
Взаимно простые числа
Рассмотрим ситуацию.
В первой банке лежало 9 декоративных камней, во второй – 14 . Сколько предметов интерьера, можно украсить имеющимся материалом, если на каждое изделие использовать равное, при этом, наибольшее количество,камней из первой и второй коробки?
Чтобы ответить на главный вопрос задачи, нужно выполнить определенные вычисления. Для этого, разложим данные значения на простые составляющие:
14 | 2 9 | 3
7 | 7 3 | 3
1 1
Выписываем компоненты, входящие в состав известных значений:
14 = 2 × 7
9 = 3 × 3
Повторяющихся составляющих нет. Мы знаем, если любое натуральное число умножить на 1, числовое значение не изменится. Значит, единственный, наибольший общий множитель чисел – 1.
Данным количеством камней получится украсить только один предмет интерьера, если использовать равное, наибольшее количество материала из обеих банок.
В арифметике числа, наибольшим общим множителем которых является 1, называют взаимно простыми.
Чтобы ответить на главный вопрос задачи, нужно выполнить определенные вычисления. Для этого, разложим данные значения на простые составляющие:
14 | 2 9 | 3
7 | 7 3 | 3
1 1
Выписываем компоненты, входящие в состав известных значений:
14 = 2 × 7
9 = 3 × 3
Повторяющихся составляющих нет. Мы знаем, если любое натуральное число умножить на 1, числовое значение не изменится. Значит, единственный, наибольший общий множитель чисел – 1.
Данным количеством камней, получится украсить только один предмет интерьера, если использовать равное, наибольшее количество материала из обеих банок.
В арифметике, числа, наибольшим общим множителем которых является 1, называют взаимно простыми
Чтобы ответить на главный вопрос задачи, необходимо определить самое маленькое числовое значение, которое будет, без остатка делиться на 4, на 5, то есть будет кратно 4, 5.
Сначала, подберем значения, кратные четырем: 4,8,12,16,20,24,28.
Теперь, значения, кратные пяти: 5,10,15,20,25,30.
После этого, необходимо найти самое маленькое число, которое будет кратным 4, 5 одновременно.
Из перечисленных числовых значений, подходит только 20. Оно делится без остатка на 4, на 5. Наименьшим общим кратным двух чисел будет 20.
Важно!
В математике существует специальный алгоритм для нахождения наименьшего общего кратного нескольких натуральных числовых значений:
Например:
Вычислим НОК для 30 и 32.
Чтобы выполнить нужные вычисления воспользуемся алгоритмом нахождения НОК.
Разберем задачу
В городе Москва, для качественной съемки парада, приуроченного к празднику 9 Мая, организаторы подготовили квадрокоптеры с видеокамерами. Из одной точки одновременно, будут запущены три аппарата. Время полета первого 8 минут, второго – 12.Через какое время,квадрокоптеры снова будут запущены одновременно, если по возвращению в точку запуска им меняют батарею и сразу отправляют назад.
Чтобы получить ответ на главный вопрос задачи, найдем наименьшее числовое значение, кратное двум данным величинам.
Для этого будем использовать рассмотренный алгоритм:
Квадрокоптеры будут одновременно запущены через 24 минуты.
Последняя задачка на внимательность.
На уроке Ваня около доски выполнял задание. Он написал: НОК (25; 115) = 100. Подскажите Ване, верно ли он выполнил задание (не выполняя вычислений)?
Вначале, давайте вспомним определение НОК:
Из определения следует, НОК нацело делится на известные данные. Однако,видим, что 100 на 115 нацело разделить невозможно. Поэтому Ваня, допустил ошибку в своих расчетах!
Вот так легко и просто можно решить огромное количество задач, даже не совершая сложных вычислений!
Пока, вы только ученики 6 класса. Пройдет совсем немного времени и каждому придется делать главный выбор в своей жизни – «Кем стать?». Если решите связать жизнь с программированием, интернет-ресурсами, научной деятельностью, вам нужно запомнить все правила и определения. Рассмотренные сегодня алгоритмы лежат в основе разработки, создания, компьютерных программ, сайтов, игр.
Минутка истории
1. Древнегреческий математик Эвклид, создавший алгоритм нахождения НОД, совершил множество математических открытий, аналогов которым ученые не нашли. Самым интересным, является то, что биографических сведений о самом Эвклиде не существует.
2. Среди бесконечного множества простых чисел, заканчивающихся на два и пять, существует только два: 2 и 5.
3. Результат суммирования цифр числа 18, в два раза меньше этого числа. Существует только одно число такого плана.
4. Однажды, математик Абрахам де Муавр, живший в Англии, находясь в преклонном возрасте, выяснил, что временной период, занимающий сон, увеличивается ежедневно на четвертую часть часа. Проведя вычисления, он определил день, когда длительность сна достигнет суток. По его расчетам это должно произойти двадцать седьмого ноября 1754 года. Именно эта дата стала датой смерти английского ученого.
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Общие делители
Пример 1
Найти общие делители чисел $15$ и $–25$.
Решение.
Делители числа $15: 1, 3, 5, 15$ и им противоположные.
Делители числа $–25: 1, 5, 25$ и им противоположные.
Ответ: у чисел $15$ и $–25$ общими делителями будут числа $1, 5$ и им противоположные.
Согласно свойствам делимости числа $−1$ и $1$ – делители любого целого числа, значит, $−1$ и $1$ всегда будут общими делителями для любых целых чисел.
Любой набор целых чисел всегда будет иметь как минимум $2$ общих делителя: $1$ и $−1$.
Отметим, что если целое число $a$ – общий делитель некоторых целых чисел, то –а также будет общим делителем для этих чисел.
Чаще всего на практике ограничиваются только положительными делителями, но при этом не стоит забывать, что каждое противоположное положительному делителю целое число также будет делителем данного числа.
Определение наибольшего общего делителя (НОД)
Согласно свойствам делимости у каждого целого числа есть хотя бы один делитель, отличный от нуля, и количество таких делителей конечно. В таком случае общих делителей заданных чисел также конечное число. Из всех общих делителей заданных чисел можно выделить наибольшее число.
Далее будем рассматривать случаи, когда хотя бы одно из данных чисел не равно нулю.
В случае равенства всех данных чисел нулю нельзя определить наибольший из общих делителей, т.к. нуль делится на любое целое число, которых бесконечное множество.
«Наибольший общий делитель, взаимно простые числа» 👇
Обозначается наибольший общий делитель чисел $a$ и $b$ в математике $НОД(a, b)$.
Пример 2
Найти НОД целых чисел 412$ и $–30$..
Решение.
Найдем делители каждого из чисел:
$12$: числа $1, 3, 4, 6, 12$ и им противоположные.
$–30$: числа $1, 2, 3, 5, 6, 10, 15, 30$ и им противоположные.
Общими делителями чисел $12$ и $–30$ будут $1, 3, 6$ и им противоположные.
Найдем наибольшее из этих чисел, сравнив только положительные из них: $1
$НОД (12, –30)=6$.
Определить НОД трех и более целых чисел можно аналогично определению НОД двух чисел.
НОД трех и более целых чисел является наибольшее целое число, которое делит одновременно все числа.
Обозначают наибольший делитель $n$ чисел $НОД(a_1, a_2, …, a_n)= b$.
Пример 3
Найти НОД трех целых чисел $–12, 32, 56$.
Решение.
Найдем все делители каждого из чисел:
$–12$: числа $1, 2, 3, 4, 6, 12$ и им противоположные;
$32$: числа $1, 2, 4, 8, 16, 32$ и им противоположные;
$56$: числа $1, 2, 4, 7, 8, 14, 28, 56$ и им противоположные.
Общими делителями чисел $–12, 32, 56$ будут $1, 2, 4$ и им противоположные.
Найдем наибольшее из этих чисел, сравнив только положительные из них: $1
$НОД(–12, 32, 56)=4$.
В некоторых случаях НОД целых чисел может быть одно из этих чисел.
Взаимно простые числа
Определение 3
Целые числа $a$ и $b$ – взаимно простые, если $НОД(a, b)=1$.
Пример 4
Показать, что числа $7$ и $13$ – взаимно простые.
Решение.
Согласно таблицы простых чисел $7$ и $13$ являются простыми числами. Это значит, что их делителями являются только числа $–1, 1$, сами числа и противоположные к ним числа. Следовательно, НОД чисел $7$ и $13$ будет число $1$:
$НОД (7, 13) = 1$.
По определению взаимно простых чисел $7$ и $13$ – взаимно простые.
Ответ: $7$ и $13$ – взаимно простые.
Пример 5
Определить, будут ли числа $3$ и $20$ взаимно простыми.
Решение.
Найдем все делители числа $3$: числа $1, 3$ и им противоположные.
Найдем все делители числа $20$: числа $1, 2, 4, 5, 10, 20$ и им противоположные.
Как видим, число $1$ является единственным общим делителем чисел $3$ и $20$, следовательно, $НОД (3, 20) = 1$.
Ответ: $3$ и $20$ – взаимно простые.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме