Как найти нод числа в степени

Одночлен

Стандартным видом записи одночлен является такая, в которой на первом месте произведения стоит число, далее в произведении записаны переменные по их следовании в алфавите.

Например, одночлен ${34a}^5b^4$ записан в стандартном виде, а одночлен ${b^434a}^5$ — нет.

Число, стоящее на первом месте при стандартной записи одночлена, называется коэффициентом одночлена. Коэффициент одночлена ${34a}^5b^4$ равен $34$, а у одночлена $,-11 sqrt{y }$ равен $-11$.

Наибольший общий делитель

Наибольшее натуральное число, на которое делятся без остатка числа $a$ и $b$, называется наибольшим общим делителем и часто обозначается НОД.

Чтобы найти наибольший общий делитель двух чисел, необходимо:

1) разложить числа на простые множители

2) выбрать числа, которые входят в разложение этих чисел

3) найти произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наибольшим общим делителем.

Наибольший общий делитель одночленов

«Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) одночленов» 👇

Наибольшим общим делителем одночленов будет являться одночлен, содержащий общие переменные с наибольшими показателями степеней.

Например, для одночленов $a^4b^3$ и $a^2b^5c^3$ наибольшим общим делителем будет $a^2b^3$.

Чтобы найти наибольший общий делитель двух одночленов, необходимо:

1) найти переменные, входящие в состав каждого из исходных одночленов;

2) выбрать из показателей степеней выбранных переменных наименьшие и НОД коэффициентов исходных одночленов;

3) найти произведение переменных и чисел, найденных на шаге $2$. Полученный одночлен и будет искомым наибольшим общим делителем одночленов.

Наименьшее общее кратное двух чисел

Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК

Чтобы найти НОК двух чисел, необходимо:

1. Разложить числа на простые множители

2. Выписать множители, входящие в состав первого числа, и добавить к ним множители, которые входят в состав второго и не ходят в состав первого;

3. Найти произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наименьшим общим кратным

Наименьшее общее кратное двух одночленов

Чтобы найти НОК двух одночленов, необходимо:

1) Найти переменные, входящие в состав каждого из исходных одночленов;

2) Выбрать из показателей степеней выбранных переменных наибольшие степени и добавить к ним множители, которые входят в состав второго и не ходят в состав первого;

3) Найти произведение переменных, найденных на шаге $2$. Полученный одночлен и будет искомым наименьшим общим кратным одночленом.

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

• 

  2 слайд

  Проверка домашнего задания
  № 797
  Выполни действия:
  63 – 25 =
  64 + 2 ∙ 92 =
  (22 + 23) ∙ 143 =
  32 – 23 + 34 ∙ 6 =
  84
  226
  12
  487

• 

  3 слайд

  Проверка домашнего задания
  № 802
  Найти НОД и НОК чисел 8, 12, 28 методом перебора:
  НОД (8, 12, 28) =

  НОК (8, 12, 28) =
  2
  168
  4
  Д(8) = {1, 2, 4, 8}
  Д(12) = {1, 2, 3, 4, 6, 12}
  Д(28) = {1, 2, 4, 7, 14, 28}
  К(8) ={8, 16, 24, 32, …,152, 160, 168, …}
  К(12) ={12, 24, 36, 48, …, 156, 168, …}
  К(28) = {28, 56, 84, 112, 140, 168, …}

• 

  4 слайд

  Проверка домашнего задания
  № 803
  Найти НОД и НОК чисел 180 и 396 методом разложения на простые множители:

  НОД(180, 396) = 2 ∙ 2 ∙ 3 ∙ 3 = 36
  НОК(180, 396) = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 11∙ 5 = 1980
  180 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5
  396 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 11

• 

  5 слайд

  3; 15; 50
  НОД(3, 50) =
  НОК(3, 50) =
  150
  НОД(3, 15) =
  НОК(3, 15) =
  НОД(15, 50) =
  НОК(15, 50) =
  1
  15
  3
  150
  5
  Если НОД (a; b) = 1,
  то НОК (a; b) = ab

• 

  6 слайд

  Вычислите значения выражений:
  25 + 7 = 32
  12 ∙ 12 = 144
  5 ∙ 49 = 245
  35 ∙ 35 = 1225

• 

• 

  8 слайд

  Физкультминутка
  Физкультминутка

• 

  9 слайд

  № 1
  НОД (6; 9; 12) = 3; НОК (6; 9; 12) = 36;
  №2
  а) НОД (252; 264) = 12; НОК (252; 264) = 5544;
  б) НОД (5; 16) = 1; НОК (5; 16) = 80
  №3
  а) 36; б) 18; в) 25; г) 11.

• 

• 

  11 слайд

  1) 28 + 36 = 64 (км/ч) – скорость сближения
  2) 64 ∙ 2 = 128 (км) – пройдут катера
  3) 192 – 128 = 64 (км)
  Ответ: 64 км будет между катерами через 2 ч.
  № 808
  192 км
  36 км/ч
  28 км/ч
  t = 2 ч

• 

  12 слайд

  № 761
  Длина прямоугольного параллелепипеда равна 90 см, ширина 25 см, а высота 12 см. Найти длину ребра куба, объем которого равен объему этого прямоугольного параллелепипеда.

• 

• 

  14 слайд

  Домашнее задание:

  №804; 805; 807.
  По желанию: № 806.

• 

  15 слайд

  Мне
  понравилось.
  Много нового
  и интересного.
  Мне
  понравилось.
  У меня всё
  получалось.
  Мне не всё
  удалось.
  Кое – где я ещё испытываю
  затруднения.
  Мне не
  понравилось.
  Мне было
  трудно.
  Определи своё настроение в конце урока.
  Поделись своими
  впечатлениями.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 266 077 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Оставьте свой комментарий

1. Нахождение наибольшего общего делителя многочленов

Определение. Если каждый из
двух многочленов делится без остатка
на третий, то он называется общим
делителем первых двух.

Наибольшим общим делителем (НОД)
двух многочленов называется их
общий делитель наивысшей степени.

НОД можно находить с помощью разложения
на неприводимые множители или с помощью
алгоритма Евклида.

Пример 40 Найти НОД многочленови.

Решение. Разложим оба многочлена
на множители:

Из
разложения видно, что искомым НОДом
будет многочлен (х– 1).

Пример 41 Найти НОД многочленови.

Решение. Разложим оба многочлена
на множители.

Для многочлена
возможными рациональными корнями будут
числа1,2,3 и6.
С помощью подстановки убеждаемся, чтох= 1 является корнем. Разделим
многочлен на (х– 1) по схеме Горнера.

	1	–6	11	–6
1	1	1 – 6 = –5	–5 + 11 = 6	6 – 6 = 0

Следовательно,
,
где разложение квадратного трехчленабыло произведено по теореме Виета.

Для многочлена
возможными рациональными корнями будут
числа1,2,3 и6.
С помощью подстановки убеждаемся, чтох= 1 является корнем. Разделим
многочлен на (х– 1) по схеме Горнера.

	1	0	–7	6
1	1	1 – 0 = 1	1 – 7 = –6	–6 + 6 = 0

Следовательно,
,
где разложение квадратного трехчленабыло произведено по теореме Виета.

Сравнив разложение многочленов на
множители, находим, что искомым НОДом
будет многочлен (х– 1)(х– 2).

Аналогично
можно находить и НОД для нескольких
многочленов.

Тем не менее, метод нахождения НОДа
путем разложения на множители доступен
не всегда. Способ, позволяющий находить
НОД для всех случаев, называется
алгоритмом Евклида.

Схема алгоритма Евклида такова. Один
из двух многочленов делят на другой,
степень которого не выше степени
первого. Далее, за делимое всякий раз
берут тот многочлен, который служил в
предшествующей операции делителем, а
за делитель берут остаток, полученный
при той же операции. Этот процесс
прекращается, как только остаток
окажется равным нулю. Покажем этот
алгоритм на примерах.

Рассмотрим многочлены, использовавшиеся
в двух предыдущих примерах.

Пример 42 Найти НОД многочленови.

Решение. Разделимна«уголком»:

x

Теперь
разделим делитель
на остатокх– 1:

x+ 1

0

Так как
последнее деление произошло без остатка,
то НОДом будет х– 1, т. е. многочлен,
использовавшийся в качестве делителя
при этом делении.

Пример 43 Найти НОД многочленови.

Решение. Для нахождения НОД
воспользуемся алгоритмом Евклида.
Разделимна«уголком»:

1

Произведем
второе деление. Для этого пришлось бы
разделить предыдущий делитель
на остаток,
но так как=,
для удобства будем делить многочленне на,
а на.
От такой замены решение задачи не
изменится, так как НОД пары многочленов
определяется с точностью до постоянного
множителя. Имеем:

0

Остаток
оказался равным нулю, значит, последний
делитель, т. е. многочлен

и будет искомым НОДом.

1. Дробно-рациональные функции

Определения и утверждения к 2.5 можно
найти в [1, с. 206-208].

Дробно-рациональной функцией с
действительными коэффициентами
называется выражение вида
,
гдеи‑ многочлены.

Дробно-рациональная функция (в дальнейшем
будем называть ее «дробь») называется
правильной, если степень многочлена,
стоящего в числителе, строго меньше
степени многочлена, стоящего в
знаменателе. В противном случае она
называетсянеправильной.

Алгоритм приведения неправильной дроби
к правильной называется «выделением
целой части».

Пример 44 Выделить целую часть дроби:.

Решение. Для того, чтобы выделить
целую часть дроби необходимо разделить
числитель дроби на ее знаменатель.
Разделим числитель данной дроби на
ее знаменатель «уголком»:

Так как
степень получившегося многочлена
меньше степени делителя, то процесс
деления закончен. В итоге:

=.
Получившаяся в результате дробьявляется правильной.

Дробь вида
называется простейшей, если φ(x
) – неприводимый многочлен, а
степеньменьше степени φ(x ).

Замечание. Обратите внимание, что
сравниваются степени числителя и
неприводимого многочлена в знаменателе
(без учета степени α).

Для дробей с действительными коэффициентами
существует 4 вида простейших дробей:

1. .

2. .

3. .

4. .

Любая правильная дробь
может быть представлена в виде суммы
простейших дробей, знаменатели которых
есть всевозможные делители.

Алгоритм
разложения дроби на простейшие:

1. Если
   дробь – неправильная, то выделяем
   целую часть, а на простейшие раскладываем
   получившуюся правильную дробь.

2. Раскладываем
   знаменатель правильной дроби на
   множители.

3. Записываем
   правильную дробь в виде суммы простейших
   дробей с неопределенными коэффициентами.

4. Приводим
   к общему знаменателю сумму дробей в
   правой части.

5. Находим
   неопределенные коэффициенты:

— либо приравнивая коэффициенты при
одинаковых степенях у левого и правого
приведенных числителей;

— либо подставляя конкретные (как правило
корни общего их знаменателя) значения
x.

1. Записываем
   ответ с учетом целой части дроби.

Пример 45 Разложить на простейшие.

Решение. Так как данная
дробно-рациональная функция является
неправильной, выделим целую часть:

1

= 1 +.

Разложим
получившуюся дробь
на простейшие. Вначале разложим на
множители знаменатель. Для этого найдем
его корни по стандартной формуле:

.

Запишем
разложение дробно-рациональной функции
на простейшие, используя неопределенные
коэффициенты:

.

Приведем
правую часть равенства к общему
знаменателю:

.

Составляем
систему, приравнивая коэффициенты при
одинаковых степенях в числителях левой
и правой дробей:

Ответ:
.

Пример 46 Разложить на простейшие.

Решение. Так как данная дробь
является правильной (т. е. степень
числителя меньше степени знаменателя),
выделять целую часть не надо. Разложим
знаменатель дроби на множители:.

Запишем
разложение данной дроби на простейшие,
используя неопределенные коэффициенты:

.
По утверждению, знаменатели простейших
дробей должны бытьвсевозможнымиделителями знаменателя дроби:

.
(2.2)
Можно было бы составить систему
уравнений, приравняв числители левой
и правой дробей, но в данном примере
вычисления будут слишком громоздки.
Упростить их поможет следующий прием:
подставим в числители по очереди корни
знаменателя.

При х = 1:

,

Прих= ‑1:

Теперь для
определения оставшихся коэффициентов
АиСдостаточно будет приравнять
коэффициенты при старшей степени и
свободные члены. Их можно найти, не
раскрывая скобок:

В левой части первого уравнения стоит
0, так как в числителе левой дроби в
(2.2) нет слагаемого с,
а в правой дроби у слагаемого скоэффициентA + C.
В левой части второго уравнения стоит
0, так как в числителе левой дроби в
(2.2) свободный член равен нулю, а у
числителя правой дроби в (2.2) свободный
член равен (‑A +
B + C
+ D). Имеем:

Ответ:.

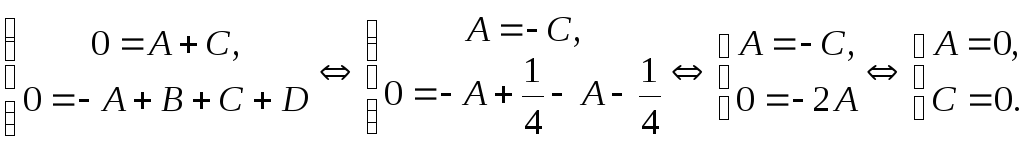
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #