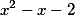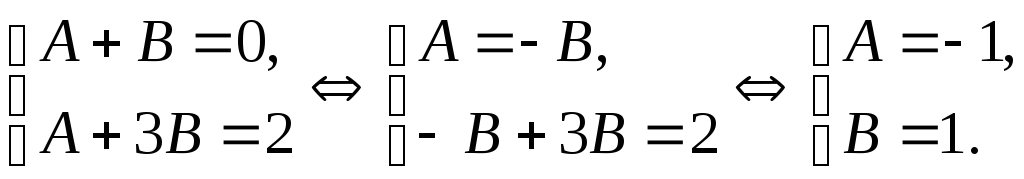Как найти нод многочленов онлайн

Калькулятор вычисляет наибольший общий делитель (НОД) двух многочленов методом Евклида. Коэффициенты многочлена могут быть целыми, простыми дробями или комплексными числами с целыми или дробными коэффициентами. Результатом является полином, который делит оба исходных полинома без остатка или единица, если такого полинома не нашлось.

Наибольший общий делитель (НОД) двух многочленов

Алгоритм корректировки остатков (псевдо-остатков)

Оценка метода вычисления остатков

Вычисляет НОД коэффициентов на каждом шаге.

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Проблема взрывного роста коэффициентов остатков

При вычислении НОД для полиномов значительных степеней, коэффициенты остатков довольно быстро растут, это можно увидеть на примере данных по-умолчанию. Поэтому, для сокращения размера коэффициентов используют псевдоделение, что позволяет находить НОД в целых числах и минимизировать коэффициенты. В калькуляторе можно выбрать один из 3-х способов сокращения остатков, не считая тривиального псевдоделения, где просиходит избавление от дробей, но коэффициенты остатков не сокращаются.

Максимальное сокращение коэффициентов можно получить, поделив, коэффициенты остатка на общий НОД коэффициентов, но этот способ может быть вычислительно сложным для полиномов больших степеней со сложными коэффициентами.

В качестве компромиссного варианта используют алгоритмы на основе вычисления субрезультанта псевдоостатков полиномов (Subresultant PRS). Наш калькулятор использует два таких алгоритма (Алгоритм 1 и Алгоритм 3), описанные В.С. Брауном в статье The Subresultant PRS Algorithm¹.
Для оценки работы алгоритма калькулятор выводит таблицу псевдоостатков и вычисляет НОД их коэффициентов. Чем меньше НОД в этой таблице, тем эффективнее работает алгоритм.

Источник

Исходный полином f(x) (его коэффициенты)

Делим на следующий полином / многочлен

Первый многочлен

Второй многочлен

Остатки от деления двух полиномов

Рассматривается вычисление наибольшего общего делителя (НОД) двух многочленов. Принцип который используется, такой же как и для нахождения НОД обычных чисел.

Отличие нашего калькулятора в том, что

1. Он показывает промежуточные остатки при вычислении

2. Многочлены могут быть комплексными, то есть содержать мнимые числа.

Теории больше не будет, и сразу перейдем к примерам вычисления, и вы поймете, как это вычисляется.

Найти НОД двух многочленов

$g(x)%20=%202*x^{3}-*x^{2}-2*x+2$

Сначала выбираем тот полином у которого степень выше и коэффицент при этой степени наибольший.

Делим один на другой f(x) на g(x). Можно делать это руками а можно воспользоваться калькулятором деления многочлена на многочлен.

Получаем остаток

Теперь делим уже g(x) на полученный остаток

получаем

Еще раз проделываем процедуру

получаем остаток

Если мы еще раз проведем такую же процедуру то получим в остатке ноль.

Закончили деление и смотрим на результат.

Предпоследнее значение от деления двух многочленов и есть значение НОД.

То есть наш ответ

Кто хочет получить результат в виде дроби то стоит обратить внимание на Непрерывные, цепные дроби онлайн которая нам это значение в виде дроби и окончательный красивый ответ есть

НОД двух функций

$g(x)%20=%202*x^{3}-*x^{2}-2*x+2$

равен $-frac{81}{1600}$

Как же пользоватся ботом?

Выписыаем коэффициенты полиномов в строку разделяя их пробелом.

Получили

1 1 -4 0 5 это у нас первый полином

2 -1 -2 2 а это второй

Вводим их в соответсвующие поля и нажимаем рассчитать.

Смотрим результат

Первый многочлен

Второй многочлен

Остатки от деления двух полиномов

То есть всё то что мы делали руками.

Замечание: Как видно, в остаток всегда «примешивается» какая то мелкая погрешность. Это надо учитывать, в окончательном оформлении своего решения.Но это не всегда так. Если коэффициенты при старших степенях полиномов на любом этапе вычислений равны единицы, то погрешность результата нулевая.

Попробуем найти НОД комплексных многочленов

Пишем любые коэффициенты с мнимыми значениями и получаем

Первый многочлен

Второй многочлен

Остатки от деления двух полиномов

Еще один пример, с «нюансом»

Первый многочлен

Второй многочлен

Остатки от деления двух полиномов

Смотрите!! НОД не равен так как на предыдущей строке, уже получается ноль, правда с погрешность после 11 знака после запятой, но мы то с Вами понимаем (!!!) что это все равно ноль.

И наш правильный ответ или вынеся за скобку общий множитель получаем что НОД равен

Да, некоторые возразят «Ну, тут еще и думать надо..» Хотелось бы возразить, но не буду, так как согласен с ними что «Думать надо!»

Надеюсь, Ваши расчеты стали еще проще и быстрее!

Источник

УчебаМатематикаАлгебра

Расширенный НОД полиномов в конечном поле

Используя расширенный алгоритм Евклида, калькулятор вычисляет НОД и полиномы A и B, участвующие в соотношении Безу

Калькулятор ниже вычисляет НОД (Наибольший общий делитель) , многочлен A, многочлен B в конечном поле заданного порядка для двух входных полиномов u и v, таких что НОД(u,v) = Au+Bv.

Наибольший общий делитель полинома в конечном поле, расширенный алгоритм Евклида

Многочлен 1

Многочлен 2

Порядок конченого поля

Ноль для кольца целых чисел

Точность вычисления

Точно

Округленно

Наибольший общий делитель

Полином A

Полином B

Ссылка скопирована в буфер обмена

Для многочлена
возможными рациональными корнями будут
числа1,2,3 и6.
С помощью подстановки убеждаемся, чтох= 1 является корнем. Разделим
многочлен на (х– 1) по схеме Горнера.

	1	–6	11	–6
1	1	1 – 6 = –5	–5 + 11 = 6	6 – 6 = 0

Следовательно,
,
где разложение квадратного трехчленабыло произведено по теореме Виета.

	1	0	–7	6
1	1	1 – 0 = 1	1 – 7 = –6	–6 + 6 = 0

Следовательно,
,
где разложение квадратного трехчленабыло произведено по теореме Виета.

Сравнив разложение многочленов на
множители, находим, что искомым НОДом
будет многочлен (х– 1)(х– 2).

Аналогично
можно находить и НОД для нескольких
многочленов.

Тем не менее, метод нахождения НОДа
путем разложения на множители доступен
не всегда. Способ, позволяющий находить
НОД для всех случаев, называется
алгоритмом Евклида.

Схема алгоритма Евклида такова. Один
из двух многочленов делят на другой,
степень которого не выше степени
первого. Далее, за делимое всякий раз
берут тот многочлен, который служил в
предшествующей операции делителем, а
за делитель берут остаток, полученный
при той же операции. Этот процесс
прекращается, как только остаток
окажется равным нулю. Покажем этот
алгоритм на примерах.

Рассмотрим многочлены, использовавшиеся
в двух предыдущих примерах.

Пример 42 Найти НОД многочленови.

Решение. Разделимна«уголком»:

Теперь
разделим делитель
на остатокх– 1:

x+ 1

Так как
последнее деление произошло без остатка,
то НОДом будет х– 1, т. е. многочлен,
использовавшийся в качестве делителя
при этом делении.

Пример 43 Найти НОД многочленови.

Решение. Для нахождения НОД
воспользуемся алгоритмом Евклида.
Разделимна«уголком»:

Произведем
второе деление. Для этого пришлось бы
разделить предыдущий делитель
на остаток,
но так как=,
для удобства будем делить многочленне на,
а на.
От такой замены решение задачи не
изменится, так как НОД пары многочленов
определяется с точностью до постоянного
множителя. Имеем:

Остаток
оказался равным нулю, значит, последний
делитель, т. е. многочлен

и будет искомым НОДом.

Дробно-рациональные функции

Определения и утверждения к 2.5 можно
найти в [1, с. 206-208].

Дробно-рациональной функцией с
действительными коэффициентами
называется выражение вида
,
гдеи‑ многочлены.

Дробно-рациональная функция (в дальнейшем
будем называть ее «дробь») называется
правильной, если степень многочлена,
стоящего в числителе, строго меньше
степени многочлена, стоящего в
знаменателе. В противном случае она
называетсянеправильной.

Алгоритм приведения неправильной дроби
к правильной называется «выделением
целой части».

Пример 44 Выделить целую часть дроби:.

Решение. Для того, чтобы выделить
целую часть дроби необходимо разделить
числитель дроби на ее знаменатель.
Разделим числитель данной дроби на
ее знаменатель «уголком»:

Так как
степень получившегося многочлена
меньше степени делителя, то процесс
деления закончен. В итоге:

=.
Получившаяся в результате дробьявляется правильной.

Дробь вида
называется простейшей, если φ(x
) – неприводимый многочлен, а
степеньменьше степени φ(x ).

Замечание. Обратите внимание, что
сравниваются степени числителя и
неприводимого многочлена в знаменателе
(без учета степени α).

Для дробей с действительными коэффициентами
существует 4 вида простейших дробей:

Любая правильная дробь
может быть представлена в виде суммы
простейших дробей, знаменатели которых
есть всевозможные делители.

Алгоритм
разложения дроби на простейшие:

Если
дробь – неправильная, то выделяем
целую часть, а на простейшие раскладываем
получившуюся правильную дробь.
Раскладываем
знаменатель правильной дроби на
множители.
Записываем
правильную дробь в виде суммы простейших
дробей с неопределенными коэффициентами.
Приводим
к общему знаменателю сумму дробей в
правой части.
Находим
неопределенные коэффициенты:

— либо приравнивая коэффициенты при
одинаковых степенях у левого и правого
приведенных числителей;

— либо подставляя конкретные (как правило
корни общего их знаменателя) значения
x.

Записываем
ответ с учетом целой части дроби.

Пример 45 Разложить на простейшие.

Решение. Так как данная
дробно-рациональная функция является
неправильной, выделим целую часть:

= 1 +.

Разложим
получившуюся дробь
на простейшие. Вначале разложим на
множители знаменатель. Для этого найдем
его корни по стандартной формуле:

Запишем
разложение дробно-рациональной функции
на простейшие, используя неопределенные
коэффициенты:

Приведем
правую часть равенства к общему
знаменателю:

Составляем
систему, приравнивая коэффициенты при
одинаковых степенях в числителях левой
и правой дробей:

Ответ:
.

Пример 46 Разложить на простейшие.

Решение. Так как данная дробь
является правильной (т. е. степень
числителя меньше степени знаменателя),
выделять целую часть не надо. Разложим
знаменатель дроби на множители:.

Запишем
разложение данной дроби на простейшие,
используя неопределенные коэффициенты:

.
По утверждению, знаменатели простейших
дробей должны бытьвсевозможнымиделителями знаменателя дроби:

.
(2.2)
Можно было бы составить систему
уравнений, приравняв числители левой
и правой дробей, но в данном примере
вычисления будут слишком громоздки.
Упростить их поможет следующий прием:
подставим в числители по очереди корни
знаменателя.

При х = 1:

Прих= ‑1:

Теперь для
определения оставшихся коэффициентов
АиСдостаточно будет приравнять
коэффициенты при старшей степени и
свободные члены. Их можно найти, не
раскрывая скобок:

В левой части первого уравнения стоит
0, так как в числителе левой дроби в
(2.2) нет слагаемого с,
а в правой дроби у слагаемого скоэффициентA + C.
В левой части второго уравнения стоит
0, так как в числителе левой дроби в
(2.2) свободный член равен нулю, а у
числителя правой дроби в (2.2) свободный
член равен (‑A +
B + C
+ D). Имеем:

Ответ:.

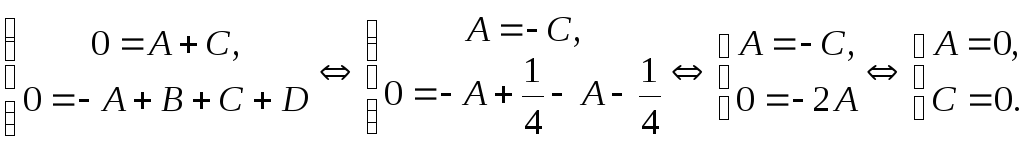
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Radians}	mathrm{Degrees}	square!	(	)	%	mathrm{clear}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Subscribe to verify your answer

Number Line

Examples

gcd:frac{1}{3}x^{7},:frac{2}{3}x^{8},:frac{4}{3}x^{4},:frac{1}{3}x
gcd:x^{2}+7x+6,:x^{2}−5x−6
gcd:8x^{2}yz^{6},:24xy^{6},:48x^{3}y^{2}z^{2}
gcd:x^{2}-1,:x^{2}+2x+1
Show More

Description

Find the gcd of two or more polynomials step-by-step

polynomial-gcd-calculator

Наибольший общий делитель (НОД) двух многочленов

Проблема взрывного роста коэффициентов остатков

Расширенный НОД полиномов в конечном поле

Наибольший общий делитель полинома в конечном поле, расширенный алгоритм Евклида

Похожие калькуляторы

Комментарии

Нахождение наибольшего общего делителя многочленов

Дробно-рациональные функции

Number Line