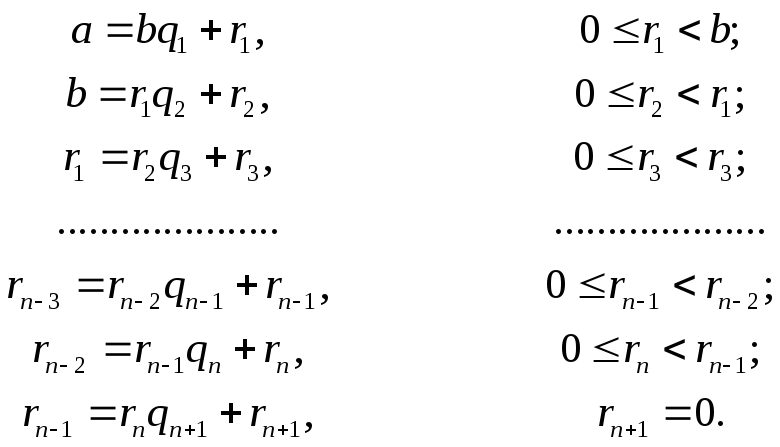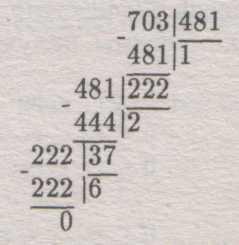Как найти нод множества чисел

1 — НОД — наибольший общий делитель.

Алгоритм для поиска НОД 2 чисел известен, но приведу его ещё раз.

long long gcd(long long a,long long b){
    while (a && b)
        if (a > b) a%=b;
        else b%=a;
    return a+b; 
}

Тут используется допущение, что НОД(0,0)=0, это часто удобно.

Теперь, чтобы найти НОД нескольких чисел, нужно последовательно брать НОД от них.

 long long gcd(const vector<long long>& num){
    if (num.size() == 0)
       return 0;
    if (num.size() == 1)
       return num[0];
    long long res = gcd(num[0],num[1]);
    for (auto i=2;i<num.size() && res!=1;i++)  //&& res!=1 можно не писать
         res = gcd(res,num[i]);
 }

найти числа, при деление на которые все элементы множества дают
одинаковый остаток.

Есть разные варианты, как это сделать. НО идея у вас перебирать от 2 до НОД неправильная. Пример: 5 и 9 дают остаток 1 при делении на 4. Но НОД(5,9)=1.

Если в наборе более 1 числа (предполагаю что все числа различны) то количество таких делителей будет не больше чем минимальное из этих чисел. Но это долго.

Пусть x = a*p + r, y = b*p + r Тогда x-y = (b-a)*p И значит делится на p аналогично для остальных пар. Поэтому ответ — все делители от НОД разностей всех чисел (Их N^2, но все необязательны, достаточно между соседними или от 1 ко всем, всего N-1 штука).

Доказательство. Пусть G = gcd(delt).

Тогда если x ≡ r (mod G). y = x + (y - x) => y = x + G*q => y ≡ r + G*q (mod G) => y ≡ r (mod G). Что и требовалось.

В обратную: для любых (x,y) x ≡ r (mod Q) y ≡ r (mod Q) G not | Q => x-y ≡ 0 (mod Q) => x-y делится на Q. Отсюда противоречие с тем что G - gcd();

Реализацию сами допишите.

Сложность — память O(n) или O(1) время O(n * log2(M) + sqrt(M) ). где M — максимальное значение. sqrt(M) — факторизация ответа, можно и без неё алгоритмы найти легко.

Вычисление НОД — ошибка, которой не замечают

Что такое НОД, все знают еще со школы. Для тех, кто подзабыл, напомню: НОД — наибольший общий делитель, делящий два целых числа без остатка. Например, НОД чисел 100 и 45 равен 5, а НОД чисел 17 и 7 равен 1. Существует несколько различных алгоритмов поиска этого числа. Однако, несмотря на то, что это достаточно простые алгоритмы, часто совершают одну маленькую, но очень существенную ошибку.

Алгоритмы вычисления НОД

Я рассмотрю 5 алгоритмов вычисления НОД:

public static int gcd_1(int a, int b) {
	if (b == 0)
		return a;
	return gcd_1(b, a % b);
}

public static int gcd_2(int a, int b) {
	int t;
	while (b != 0) {
		t = b;
		b = a % b;
		a = t;
	}
	return a;
}

public static int gcd_3(int a, int b) {
	while (a != b) {
		if (a > b) {
			a = a - b;
		} else {
			b = b - a;
		}
	}
	return a;
}

public static int gcd_4(int a, int b) {
	if (a == b)
		return a;
	if (a == 0)
		return b;
	if (b == 0)
			return a;
	if ((~a & 1) != 0) {
		if ((b & 1) != 0)
			return gcd_4(a >> 1, b);
		else
			return gcd_4(a >> 1, b >> 1) << 1;
	}
	if ((~b & 1) != 0)
		return gcd_4(a, b >> 1);
	if (a > b)
		return gcd_4((a - b) >> 1, b);
	return gcd_4((b - a) >> 1, a);
}

public static int gcd_5(int a, int b) {
	int shift;
	if (a == 0)
		return b;
	if (b == 0)
		return a;
	for (shift = 0; ((a | b) & 1) == 0; ++shift) {
		a >>= 1;
		b >>= 1;
	}
	while ((a & 1) == 0)
		a >>= 1;
		do {
		while ((b & 1) == 0)
			b >>= 1;
		if (a > b) {
			int t = b;
			b = a;
			a = t;
		}
		b = b - a;
	} while (b != 0);
	return a << shift;
}

Естественно, чаще всего пишут первый вариант — он легко запоминается, быстро пишется и достаточно быстро работает.

Претесты

Реализации корректно работают на таких тестах:

gcd(1, 10) = 1
gcd(5, 10) = 5
gcd(24, 24) = 24
gcd(0, 0) = 0
gcd(5,10) = 5

Естественно, они будут работать и на подобных тестах, где в качестве аргументов выступают целые неотрицательные числа. Но что, если…

Первые тесты с подвохом

… если заменить одно из чисел нулем? Например так:

gcd(5, 0) = 5
gcd(0, 15) = 15

Классический алгоритм Евклида (№3) уже попадает в бесконечный цикл.

Копаем глубже

Согласно определению, НОД может быть определен для любых двух целых чисел. Так почему бы не попробовать тесты, где одно из чисел — отрицательное:

gcd(-5,10) = ?

Все становится еще интереснее. Первые две реализации выдают в качестве ответа -5. Третий алгоритм снова попадает в бесконечный цикл. Вместе с ним в бесконечном цикле оказывается пятый алгоритм. Четвертый падает по StackOverFlow — скорее всего тоже попадает в бесконечный цикл.
Но ведь ответ -5 — неправильный. По определению НОД — наибольший общий делитель. А таковым является число 5. Ведь и первое, и второе число

делятся без остатка

на 5. Значит и первые две реализации не дают верный ответ.

Почему решения №№3-5 попадают в бесконечный цикл?

Алгоритм Евклида попадает в цикл из-за бесконечного увеличения аргументов, если один из них отрицательный. Действительно, если посмотреть на эти строки, то можно заметить, что при отрицательном a (или b) операция вычитания заменяется сложением.

if (a > b) {
	a = a - b;
} else {
	b = b - a;
}

Аналогичное происходит в четвертом и пятом алгоритме:

if (a > b)
	return gcd_4((a - b) >> 1, b);
return gcd_4((b - a) >> 1, a);

if (a > b) {
	int t = b;
	b = a;
	a = t;
}
b = b - a;

В ситуации, когда a или b равны 0, то происходит бесконечное вычитание нуля, которое никаким образом не меняет значения аргументов.

Так что же не так?

Все эти алгоритмы корректны для входных данных, когда оба числа a и b — целые неотрицательные числа. Но вспомним еще раз — НОД существует для любых двух целых чисел.

Что же делать?

В качестве аргументов в функцию можно передавать абсолютное значение чисел, тогда ответ будет корректен:

int ans = gcd(Math.abs(a), Math.abs(b));

Второй способ решения задачи — возвращать абсолютное значение ответа:

public static int gcd(int a, int b) {
	if (b == 0)
		return Math.abs(a);
	return gcd(b, a % b);
}

Второй вариант гораздо предпочтительнее: будет производиться меньше лишних вычислений, чем в первом варианте.

Итоги

Мы рассмотрели пять различных вариантов вычисления наибольшего общего делителя. Для каждого из них мы указали входные данные, на которых ответ существует, но решение «падает», а также способ решения проблемы.
Такие небольшие ошибки чаще всего допускаются по причине того, что не замечают «скользкие» места решения какой-то задачи. Часть из них отлавливается в процессе тестирования, а часть остается незамеченной.
В ситуации с вычислением НОД

почти

все реализации приведены с ошибкой. В Сети я нашел лишь парочку корректно работающих решений, остальные идентичны тем, что приведены в начале поста.

Используемая литература, источники, реализации:

• Binary GCD algorithm — Wikipedia
• Euclidean algorithm — Wikipedia
• Алгоритм Евклида — e-maxx
• Binary GCD — Dictionary of Algorithms and Data Structures
• Кормен — Алгоритмы — построение и анализ

Была ли эта статья полезной?

1. Наибольший общий
   делитель и алгоритм Евклида.

2. Свойства наибольшего
   общего делителя.

3. Взаимно простые
   числа.

4. Наименьшее общее
   кратное.

Содержание

1.
Если каждое из целых неотрицательных
чисел а
и
b
делится
на число с,
то число с
называют
общим
делителем чисел.
Чтобы найти общие делители чисел а
и b,
достаточно
найти пересечение двух множеств:
множества делителей числа а
и
множества делителей числа b.
Это пересечение состоит из натуральных
чисел, которые не могут превосходить
меньшего из чисел а
и
b,
а
значит, в нем имеется наибольшее число.
Это число называют наибольшим общим
делителем чисел а
и b.

Определение
3.
Наибольшим
общим делителем (НОД)
чисел а
и
b
называется
самое большое натуральное число d,
являющееся
делителем для каждого из чисел а
и
b.

Наибольший
общий
делитель чисел а
и
b
будем обозначать одним из символов –
НОД(а;b)
или
(а;
b).

Непосредственно
из определения следует, что если хотя
бы одно из чисел а
и
b
отлично
от нуля, то НОД(а;b)
существует и является единственным.
Возникает вопрос: как практически
находить НОД?

Один
из способов нахождения НОД вытекает
непосредственно из определения 3.
Действительно, можно было бы сначала
найти все делители числа а,
затем – числа b.
После
этого отобрать общие делители и выбрать
из них наибольший. Такой путь, однако,
был бы весьма нерациональным, особенно
для больших чисел.

Другой,
наиболее рациональный, способ нахождения
НОД был предложен Евклидом (III
в. до н.э.).

Теорема
6.
Алгоритм
Евклида. Если
а
разделить с остатком на b
≠ 0,
затем разделить с остатком b
на
полученный остаток, затем разделить с
остатком первый остаток на второй и
т.д., то последний, отличный от нуля,
остаток равен (а;b).

Доказательство.
Проводя
последовательно деления с остатком,
указанные в формулировке теоремы,
получим:

(3)

Поскольку
последовательность остатков является
убывающей последовательностью целых
неотрицательных чисел, то через конечное
число шагов очередной остаток (например,
r_п+1)
окажется равным нулю. Пусть r_п
– последний,
отличный от нуля, остаток. Покажем, что
r_п
= (а;b).

Прежде
всего, докажем, что если а
= bq
+ r,
то
(а;b)
= (b;r).

Действительно,
если

и
,
то
по
теореме 2 о делимости разности. С другой
стороны, если
и,
то
по
теореме 1 о делимости суммы.

Таким
образом, множества общих делителей
чисел а
и
b
равны,
а значит, равны и их наибольшие общие
делители, то есть (а;b)
= (b;r).

Применяя
доказанный факт к первому из равенств
3, получим

(а;b)
= (b;r₁).
(4)

Аналогично,
из второго равенства последовательности
(3)

(b;r₁)
= (r₁;r₂).
(5)

Продолжая
аналогичные
рассуждения,
получим равенства:

;
(6)

.
(7)

Исходя
из равенств (4) – (7), можем записать: (а;b)
= (b;r₁)
= (r₁;r₂)
= … = (r_n—2;r_n—1)
= (r_n—1;r_n)
= (r_n;0)
= r_n.
Итак, (а;b)
= r_n.
Теорема
доказана.

Пример.
Найти
НОД(481; 703).

Мы
определили и показали способ нахождения
НОД двух чисел. Аналогично определяется
НОД любого конечного множества целых
неотрицательных чисел.

НОД
чисел
обозначается одним из символов – НОД()
или ().
Если,
то ()
=d_n.

Пример.
Найти
НОД чисел 840, 720, 640 и 160.

1) НОД(840; 720) = 120;

2) НОД(120; 640) = 40;

3) НОД (40; 160) = 40.

Следовательно,
НОД(840; 720; 640; 160) = 40.

2.
Рассмотрим
основные свойства НОД, выраженные
следующими теоремами.

Теорема
7.
НОД двух данных чисел делится на любой
другой общий делитель этих чисел:

.

Доказательство
теоремы вытекает из алгоритма Евклида.
Действительно, из первого равенства
последовательности (3) следует, что если
и,
то.
Во втором равенствеи,
а значит, и.
Рассуждая аналогично, мы можем установить,
что в правой части каждого из следующих
равенств алгоритма вторые слагаемые
должны делиться нас,
то есть
.
Ноr_n
= (а;b).
Следовательно,
и теорема доказана.

Теорема
8. Любой
делитель НОД двух данных чисел является
общим делителем этих чисел:

.

Доказательство.
Очевидно, что теорема 8 является обратной
для теоремы 7. Пусть
.
Докажем, чтои.

По
определениям делимости и НОД можем
записать равенства:

,
где
.
(8)

Кроме
того, по условию теоремы,
,
где
.
Заменив
в равенствах (8) НОД(а;b)
произведением

,
получим равенства
и,
которые
можно записать в виде
,.
Это означает, чтои.
Таким
образом, теорема доказана.

Теорема
9. Если
каждое из двух данных чисел умножить
на натуральное число, то НОД этих чисел
умножится на то же число:

.

Доказательство.
Пользуясь свойством монотонности
умножения, умножим обе части каждого
из равенств (3) на одно и то же число k.
В
полученных равенствах вместо натуральных
чисел

будут,
соответственно, стоять новые числа:

.

Значит,
(ak;
bk)
= r_nk,
или
(ak;
bk)
=
dk,
что
и требовалось доказать.

Теорема
10. Если
каждое из двух данных чисел разделить
на натуральное число, то НОД этих чисел
разделится на то же число:

.

Доказательство.
Поскольку
данная теорема является обратной теореме
9, то для ее доказательства достаточно
к последовательности равенств (3)
алгоритма Евклида применить преобразования
обратные тем, что были проведены в
теореме 9.

3.
Во многих вопросах теории делимости
используются числа, не имеющие общих
делителей, кроме единицы. Рассмотрим
такие числа более подробно.

Определение
4.
Если НОД чисел равен единице, то числа
называются взаимно
простыми.

–взаимно
просты
.

Если
– совокупность взаимно простых чисел,
то отсюда не следует, что любые подмножества
этой совокупности взаимно просты.

Пример.
Так,
(35; 55; 77) = 1, но (35; 55) = 5, (55; 77) = 11, (35; 77) = 7.

Теорема
11.
Если данные числа разделить на их НОД,
то полученные частные будут числами
взаимно простыми:

.

Следует
заметить, что символы
издесь представляют натуральные числа.

Справедливость
теоремы 11 вытекает из теоремы 10.
Действительно, если каждое из чисел а
и b
разделить на натуральное число d,
то и НОД этих чисел разделится на d,
а
значит, будет равен 1.

Теорема
12.
Если произведение двух чисел делится
на число, взаимно простое с одним из
множителей, то другой множитель делится
на это число:

Доказательство.
По
условию теоремы, (а;
с)
= 1.
Пользуясь
теоремой 9, умножим каждое из чисел а
и с
на число b.
Тогда
НОД этих чисел также умножится на b,
то есть (аb;
сb)
= b.
По
условию теоремы,
.
Кроме
того, очевидно, что
.
Следовательно,
с
является общим делителем чисел ab
и
сb
. Но
тогда, по теореме 7, НОД этих чисел также
делится на с,
то есть
.

Теорема
13.
(Признак
делимости на составное число.) Если
числа а
и
b
взаимно
просты, то число с
делится
на их произведение ab
тогда
и только тогда, когда с
делится
на а
и на b:

.

Доказательство.
Необходимость вытекает
из транзитивности отношения делимости.
Так как
,
то.
Аналогично,
из условия
b
следует,
что
.

Достаточность.
Пусть
и,
причем (а;b)
= 1. Докажем, что
.
Так как,
то
с
= aq₁,
где
.
Зная,
что
,
имеем,
где (а;b)
= 1.
По
теореме 12 это означает, что
,
то естьq_l
= bq₂,
где
.
Итак,
с
= aq₁
= a(bq₂)
= (ab)q₂,
то
есть
.
Теорема
полностью доказана.

Из
этой теоремы вытекает ряд признаков
делимости на числа, каждое из которых
является произведением двух взаимно
простых чисел. Например:

1.
Число х
делится
на 6 тогда и только тогда, когда оно
делится на 2 и 3.

2.
Число х
делится
на 36 тогда и только тогда, когда оно
делится на 4 и 9.

Аналогично
формулируются признаки делимости на
числа 12, 15, 18, 24, 45 и др.

4.
Пусть
а
и
b
– произвольные натуральные числа.
Натуральное число m
называется общим
кратным этих
чисел, если m
делится на каждое из чисел а
и
b.
Если
m
– общее кратное чисел а
и
b,
то,
по транзитивности отношения делимости,
каждое из чисел 2m,
3m,
4m,
… также является общим кратным чисел
а
и
b.
Среди
натуральных общих кратных, по принципу
наименьшего числа, существует наименьшее
общее кратное.

Определение
5.
Наименьшим
общим кратным (НОК)
чисел а
и
b
называется
наименьшее натуральное число т,
являющееся
общим кратным этих чисел.

Наименьшее
общее кратное
чисел а
и
b
будем
обозначать
одним
из
символов – НОК(а;b)
или
[а;
b].

Примечание.
Нуль,
как известно, является общим кратным
для любых натуральных чисел, но, по
определению, НОК(а;b)
> 0.

Теорема
14.
Любое общее кратное двух чисел делится
на их наименьшее общее кратное.

Доказательство
теоремы
проведем методом от противного. Пусть
с
– произвольное
общее кратное чисел а
и
b,
т = [а;
b].
Предположим, что с
не
делится нацело на m.
Тогда, разделив
с
на
m
с
остатком, получим с
= mq
+ r,
0 ≤ r
< m.
Поскольку
с
кратно а
и
b,
mq
кратно
а
и
b,
то, по теореме 2 о делимости разности, r
кратно
а
и
b.
Но
это противоречит тому, что m
является НОК, ибо r
< m.
Полученное противоречие доказывает
теорему.

Докажем
теперь теорему, устанавливающую связь
НОД и HОК
двух чисел. Эта теорема дает практический
способ нахождения НОК двух чисел.

Теорема
15.
НОК и НОД двух натуральных чисел а
и
b
связаны
соотношением

аb
= (а;b)
· [а;
b].

Доказательство.
По
определению НОД можем записать равенства
а
= (а;
b)
а₁,
b
=
(а;
b)b₁.
Тогда

и
.

Из
последних равенств следует, что число


является общим кратным чисел а
и
b,
а значит, по теореме 14, оно делится на
[а;
b].

Следовательно,
можем записать:

.
(9)

Докажем
теперь, что последнее равенство возможно
только при q
= 1.

По
определению НОК можем записать: [а;
b]
= aq₁
и
[а;
b]
= bq₂.
Подставляя
новые
выражения НОК в равенство (9), получим

и

.

Из последних
равенств, в свою очередь, имеем

и

.

Отсюда
и.Таким
образом, выражение (а;b)q
является
общим делителем чисел а
и
b.
Но это возможно только
при q
= 1.

Итак, равенство
(9) можем переписать в виде

,
или
ab
= (а;b)
[а;
b]

Теорема доказана.

Следствие.
НОК двух взаимно простых чисел равно
их произведению.

Пример.
Найти НОК чисел 315 и 126.

НОК(315;
126) =
.

Мы
рассмотрели определение и способ
нахождения НОК двух чисел. Аналогично
определяется НОК любого конечного
множества чисел. НОК чисел
обозначают[]
и находят по следующему правилу: сначала
находят
[а₁;а₂]
= m₂,
затем – [m₂;a₃]
= m₃,
[m₃;a₄]
= m₄,
…, [m_n—1;a_n]
= m_n.
Тогда [a₁;a₂;
…;a_n]
=m_n.

Пример.
Найти
НОК чисел 30, 120, 72 и 64.

1) НОК(30; 120) = 120;

2)
НОК(120; 72) =
;

3)
НОК(360;64) =
.

Следовательно,
НОК(30; 120; 72; 64) = 2880.