Как найти нод одного числа в паскале

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

var
  a, b, d: integer;

begin
  write('Введите два числа: ');
  readln(a, b);
  if a < b then d := a + 1 else d := b + 1; 
  {так как мы используем цикл с постусловием, 
  необходимо минимальное значение увеличить на один,
  иначе цикл repeat, в силу своих конструктивных особенностей,
  не учтет это минимальное число  
  и не сделает его кандидатом в НОД. Например, 5 и 25.}
  repeat d := d - 1
  until (a mod d = 0) and (b mod d = 0);
  write('NOD = ', d)
end.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

1. Все общие делители пары a и b являются также общими делителями пары a — b, b;
2. И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
3. НОД(A,  B) = НОД(A — B, B), если A > B;
4. НОД(A, 0) = A.

Доказательство:

1. Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
2. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
3. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
4. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

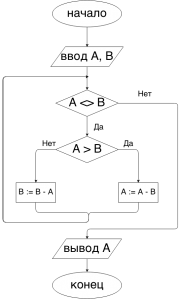
Блок — схема алгоритма Евклида «с вычитанием»

Программа

var
  a, b: integer;

begin
  write('a = '); 
  readln(a);
  write('b = ');
  readln(b);
  while a <> b do 
    if a > b then 
      a := a - b 
    else 
      b := b - a;
  writeln('NOD = ', a);
end.

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

var
  a, b: integer;

begin
  write('a = ');
  readln(a);
  write('b = ');
  readln(b);
  while (a <> 0) and (b <> 0) do
    if a >= b 
    then 
      a := a mod b 
    else 
      b := b mod a;
  write(a + b)
end.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Алгоритм Евклида

Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).

Python

#!/usr/bin/env python
a = 18
b = 30
 
while a!=0 and b!=0:
    if a > b:
        a = a % b
    else:
        b = b % a
 
print (a+b)

Perl:

 sub nod
 {
 return  $_[0] != 0  ?  nod ( ( $_[1] % $_[0] ), $_[0] )  :  $_[1];
 }

C:

 int gcd(int a, int b) {
   int c;
   while (b) {
      c = a % b;
      a = b;
      b = c;        
   }
   return abs(a);
 }

Pascal:

  function nod( a, b: longint): longint; 
  begin
   while (a <> 0) and (b <> 0) do
     if a >= b then 
       a:= a mod b 
     else 
       b:= b mod a;
   nod:= a + b;
  end;

Java:

public class GCD {
    public static int gcd(int a,int b) {
        while (b !=0) {
            int tmp = a%b;
            a = b;
            b = tmp;
        }
        return a;
    }
}

C#:

int gcd(int a, int b)
{
    while (b != 0)
        b = a % (a = b);
    return a;
}

Помогите пожалуйста написать программу которая будет вычислять наименьший общий делитель и наибольшее общее кратное. Использовать алгоритм Евклида.

В помощь:

На множестве целых чисел определены операции сложения, обратная операция вычитания и операция умножения. Операция деления, обратная операции умножения, выполняется не для всех пар чисел, то есть является на множестве целых чисел «частичной операцией».
Число а делится на число b 0, если существует число q такое, что b=qc. , (все числа целые).
В этом случае говорят, что число b делит число a. При этом число b является делителем числа а или множителем в разложении числа a на множители.
Общим делителем двух или нескольких чисел называется число, являющееся делителем каждого из этих чисел.
Если а1,…,аn целые числа и хотя бы одно из них не равно нулю, то множество их общих делителей конечно и среди этих делителей существует наибольшее число.
Наибольшим общий делителем (НОД) чисел а1,…,аn называется наибольший из их общих делителей.
НОД целых чисел а и b называется положительный делитель чисел а и b, делящийся на любой другой общий делитель этих чисел.
Cвойства НОД:
1) НОД(a,b) = НОД(b,a)
2) НОД(a,0) = |a|
3) НОД(a,b,с) = НОД(a, НОД(b,c))
4) НОД(a,b) = НОД(-a,b)
Для вычисления наибольшего общего делителя двух целых чисел можно использовать метод разложения на сомножители.
70 делится на 2, 5, 7, 10, 14, 35.
42 делится на 2, 3, 6, 7, 14, 18, 21.
НОД(70, 42) = 14.
Когда а не делится на b, то говорят о делении а на b с остатком r.
Теорема о делении с остатком. Если а и b целые положительные числа, то существуют единственные целые числа q и r такие, что
a = b*q + r, 0 ≤. r< b
Число q называют неполным частным при делении a на b,
число r называют остатком от деления а на b.
Деление по модулю (в более узком значении) — арифметическая операция, результатом которой является остаток от деления целого числа на другое целое число, то есть операция нахождения остатка от деления, а также сам остаток от деления .
Деление по модулю (в более широком значении) — арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число. То есть имеется в виду операция, которую правильнее называть делением c остатком.
Пример, в котором мы сталкиваемся с Модульной арифметикой в повседневной жизни — «арифметика часов». Допустим, сейчас 3 часа после полудня, через 14 часов будет 5 часов утра следующего дня:
(3+14) mod 12= 17 mod 12=5. Это арифметика по модулю 12.
А вот тоже самое, но по модулю 24: (15+14) mod 24= 29 mod 24=5.
Также вычисляются минуты, секунды как деление по модулю 60.

Алгоритм вычисления наибольшего общего делителя Евклида («Начала», 300 лет до н.э.) – один из древнейших классических нетривиальных алгоритмов.
В основе алгоритма Евклида лежит повторное деление с остатком: вычисляется остаток от деления (a mod b), затем b mod (a mod b) и так далее, пока остаток не будет равен нулю.
Алгоритм Евклида вычисления НОД(a,b) для a, b  0.
1. Если b =0, то результат := а и алгоритм заканчивает работу.
2. Положить r := a mod b, a := b, b := r, и вернуться на шаг 1.
Процесс вычисления наибольшего общего делителя чисел a1, a2 по алгоритму Евклида выглядит так:
a1 = a2 q1 + a3 0 ≤ a3 < a2
a2 = a3 q2 + a4 0 ≤ a4 < a3
a3 = a4 q3 + a5 0 ≤ a5 < a4

am-2 =am-1 qm-2 + am 0 ≤ am < am-1
am-1 =am qm-1
Результат: НОД(a1, a2) = am.
Остановка гарантируется, поскольку остатки от делений образуют строго убывающую последовательность натуральных чисел.
Пример: НОД(70, 42)
70 = 42 * 1 + 28 r := 70 mod 42 = 28, a := 42, b := 28
42 = 28 * 1 + 14 r := 42 mod 28 = 14, a := 28, b := 14
28 = 14 * 2 r := 28 mod 14 = 0
Результат: НОД(70, 42)=3.

Еще пример: НОД(723,288):

Результат: НОД(723,288)=3.
Эта процедура хороша как для вычисления вручную, так и для программной реализации. Соответствующая программа короткая и быстрая.
Некоторые свойства целых чисел позволяют улучшить программную реализацию алгоритма Евклида:
1) если числа а и b четные, то НОД(a, b) = 2 НОД(a/2, b/2),
2) если а четное и b нечетное, то НОД(a, b) = НОД(a/2, b),
3) НОД(a, b) = НОД(a–b, b),
4) если числа а и b нечетные, то (а – b) четное и НОД(a, b) = НОД((a–b)/2, b).

ДОПОЛНЕНИЕ
Алгоритм Евклида для целых чисел
Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

Тогда НОД(a,b), наибольший общий делитель и , равен , последнему ненулевому члену этой последовательности.
Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Пример
Для иллюстрации, алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала, от 1071 отнимем кратное значение 462, пока не получим разность меньше чем 462. Мы должны дважды отнять 462, (q0 = 2), оставаясь с остатком 147
1071 = 2 × 462 + 147.
Затем от 462 отнимем кратное значение 147, пока не получим знаменатель меньше чем 147. Мы должны трижды отнять 147 (q1 = 3), оставаясь с остатком 21.
462 = 3 × 147 + 21.
Затем от 147 отнимем кратное значение 21, пока не получим знаменатель меньше чем 21. Мы должны семь раз отнять 21 (q2 = 7), оставаясь без остатка.
147 = 7 × 21 + 0.
Таким образом последовательность a>b>R1>R2>R3>R4>…>Rn в данном конкретном случае будет выглядеть так:
1071>462>147>21

Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462)=21.
В табличной форме, шаги были следующие
Шаг k Равенство Частное и остаток
0 1071 = q0 462 + r0 q0 = 2 и r0 = 147
1 462 = q1 147 + r1 q1 = 3 и r1 = 21
2 147 = q2 21 + r2 q2 = 7 и r2 = 0; алгоритм заканчивается

Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть т и n — одно временно не равные нулю целые неотрицательные числа и пусть m≥n. Тогда, если n = 0, то НОД (n, т) = т, а если n≠0, то для чисел m, n и r, где r—остаток от деления m на n, выполняется равенство НОД (m, n) = НОД(n, r). Например, НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3. Даны натуральные числа n, m.

а) Используя алгоритм Евклида, найти наибольший общий делитель n и m.

Помогите пожалуйста!!!! Мне очень нужно!

Математика и числа

Чётность/нечётность чисел

if Odd (Number) then 
  writeln (Number, ' нечётно')
else
  writeln (Number, ' чётно');

Делимость (кратность) чисел

if Number mod 3 = 0 then
  writeln (Number, ' делится на 3 без остатка');

Наибольший Общий Делитель

{ Евклид (Euclidus) }
function GCD (A: integer;  B: integer): integer;
begin
    while (a <> 0) and (b <> 0) do
       if a >= b then
         a := a mod b
       else 
         b := b mod a;
    GCD := a + b; { один - ноль }
end;

Наименьшее Общее Кратное

function LCM (A: integer;  B: integer): integer; 
begin
     LCM := a * b div GCD (a, b)
end;

Степень

function Power(Base, N: integer): longint;
{ Base - основание , N - степень }
var
   Result: longint;
   i: word;
begin
   Result := 1; { придаём начальное значение }
   for i := 1 to N do
     Result := Result * Base;
 
   Power := Result;
end;

function PowerExp (A, N: real): real;
begin
   if A > 0 then
     PowerExp := Exp ( N * Ln (A) )
   else 
     PowerExp := 0;
end;

Факториал

function Factorial(N: word): longint;
var
   Result: longint;
   i: word;
begin
   Result := 1;
   for i := 1 to N do 
     Result := Result * N;
 
   Power := Result;
end;

function Factorial (N: word): longint;
begin
   if N = 0 then
     Factorial := 1 
   else 
     Factorial := N * Factorial (N - 1);
end;

Вещественный и целый типы

   var
       r : real;
     begin
       r := Round ( 123.456);  {    123 }
       r := Round ( 123.778);  {    124 }
       r := Trunc ( 123.456);  {    123 }
       r := Trunc (-123.778);  {   -123 }
       r := Frac  ( 123.456);  {  0.456 }
       r := Int   ( 123.456);  {  123.0 }
       r := Int   (-123.456);  { -123.0 }
     end.

Случайные числа

  Randomize;
  X := Random (N + 1) - 2 * N;

Как проверить простое ли число?

function isPrime(X: word): boolean;
var
i: integer;
Begin
     isPrime:=false;
     if not odd(x) and (x<>2) { проверяем на чётность  }
          then exit;
     i:=3;
     while i <= sqrt(x) do { проверяем только нечётные }
     begin
          if x mod i = 0 then Exit;
          inc(i,2);
     end;
 
     isPrime:=true;
End;

Разложение числа на множители

procedure Factorization(x: word);
var i: word;
 
 procedure DivX; { делим на простое число, пока делится без остатка }
 begin
      while (x>1) and (x mod i = 0) do
      begin
           write(i:4);
           x:= x div i;
      end;
 end;
 
begin
     i:=2;
     DivX;
     i:=3;
     while (i < x div 2) do
     begin
           DivX;
           inc(i,2); { <=> i:=i+2; только нечётные числа }
     end;
     if x>1 then writeln(x:4);
end;

Приближённое представление числа в виде дроби

VAR p,q,qmax:integer;
    d, r, min: real;
BEGIN
   write('r, qmax=');
   readln(r, qmax); { r - не целое число, qmax - кол-во итераций (циклов) }
   p:=0; q:=1; min:=r;
   REPEAT
     IF p / q < r
          THEN inc(p)
          ELSE inc(q);
     d:=abs(r-p/q);
     IF d < min THEN
     BEGIN
          min:=d;
          writeln(p:7,'/',q)
     END
   UNTIL (q >= qmax) OR (d = 0);
   readln;
END.

Как работать с отдельными битами?

FUNCTION IsBitOn (n: word; b : BYTE): BOOLEAN; { Проверяем, установлен ли бит }
BEGIN 
     isBitOn:=((n SHR b) AND 1) = 1
END;
 
PROCEDURE SetBitOn (VAR n: Word; b: BYTE); { Устанавливаем бит }
BEGIN
     N:= N OR (1 SHL b)
END;
 
PROCEDURE XORBit (VAR n: Word; b: BYTE); { Переключаем бит }
BEGIN
     N:= N XOR (1 SHL b)
END;

Как узнать из каких цифр состоит целое число?

Var X : Integer;
Begin
 X:=12345;
 Writeln('Число состоит из таких цифр:');
 While X <> 0 Do
  Begin
   Writeln(X Mod 10);
   X:=X Div 10;
  End;
End.

Как быстро делить/умножать числа на степень двойки ?

i:=i shl 1; { i:=i * 2^1}
i:=i shl 2; { i:=i * 2^2}
{и т.д.}
i:=i shr 1; { i:=i div 2^1}
i:=i shr 2; { i:=i div 2^2}
{и т.д.}

Более быстрое разложение числа на множители

{$N+, E+}
 
function FermaFactorization (N : Comp) : Comp;
 
var
  X, Y, R, Z, ZZ : Comp;
 
begin
 Z := Sqrt(N);
 ZZ := Trunc (Z);
 X := 2 * ZZ + 1;
 Y := 1;
 R := Sqr (ZZ) - N;
 while (R <> 0) do
  begin
   R := R + X;
   X := X + 2;
   repeat
    R := R - Y;
    Y := Y + 2;
   until R <= 0;
  end;
 FermaFactorization := (X - Y) / 2;
end;
 
begin
 Writeln (FermaFactorization(917979909) : 0 : 0);
end.