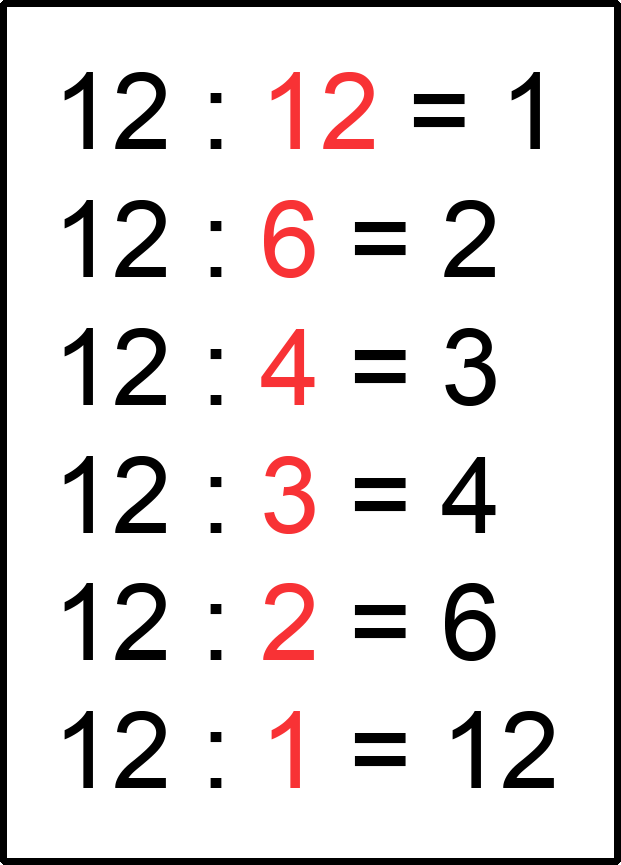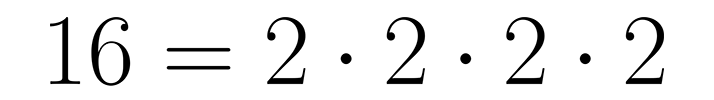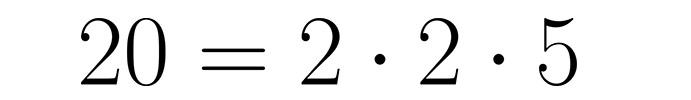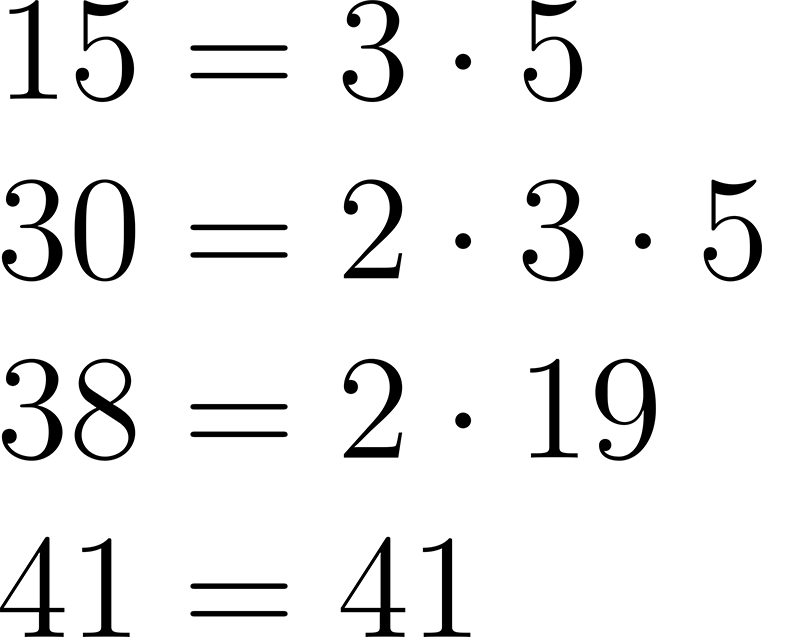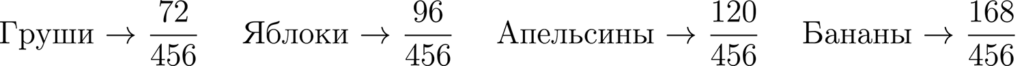Нахождение нод отрицательных чисел
Если
одно, несколько или все числа, наибольший
делитель которых нужно найти, являются
отрицательными числами, то их НОД равен
наибольшему общему делителю модулей
этих чисел. Это связано с тем,
что противоположные
числа a и −a имеют
одинаковые делители, о чем мы говорили
при изучении свойств делимости.
Пример.
Найдите
НОД отрицательных целых чисел −231 и −140.
Решение.
Модуль
числа −231 равен 231,
а модуль числа −140 равен 140,
иНОД(−231,
−140)=НОД(231, 140).
Алгоритм Евклида дает нам следующие
равенства:231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6.
Следовательно,НОД(231,
140)=7.
Тогда искомый наибольший общий делитель
отрицательных чисел−231 и −140 равен 7.
Ответ:
НОД(−231,
−140)=7.
Пример.
Определите
НОД трех чисел −585, 81 и −189.
Решение.
При
нахождении наибольшего общего делителя
отрицательные числа можно заменить их
абсолютными величинами, то есть, НОД(−585,
81, −189)=НОД(585, 81, 189).
Разложения чисел 585, 81 и 189 на
простые множители имеют соответственно
вид585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7.
Общими простыми множителями этих трех
чисел являются 3 и 3.
Тогда НОД(585,
81, 189)=3·3=9,
следовательно,НОД(−585,
81, −189)=9.
Ответ:
НОД(−585,
81, −189)=9.
-
Корені
многочлена. Теорема Безу. (33 и выше) -
Кратні
корені, критерій кратності кореня.
Кратные корни многочленов
Определение
1. Если
в разложении многочлена -степени
,
некоторые
множители окажутся одинаковыми, то
,
то -называется
корнем кратности,
-кратности
и
т.д.
Теорема
1. Если а является корнем
многочлена кратности
,
то для производнойэто
число является корнем кратности.
Доказательство. Пусть
,
где не
обращается в 0 при.
,
т.е. является
корнем кратности.
Следствие. Число а является
корнем кратности для
,…,
корнем кратности 1 для.
-
Відділення
кратних коренів.
Метод Штурма отделения корней многочлена
Рассмотрим
пример отделения корней многочлена по
методу Штурма на примере многочлена.
Для
применения этого метода к
многочлену требуется
составить систему Штурма .
Замечание:
многочлен должен
иметь действительные коэффициенты и
не иметь кратных корней.
Правило
построение системы Штурма:
1)
2)
Если известны и
,
то будет
равен остатку от деления на
,
взятым с обратным знаком:
.
Замечание:
В процессе деления, в отличии от алгоритма
Евклида, остаток можно умножать лишь
на произвольное положительное число
(для того, чтобы коэффициент при старшей
степени был целым или просто удобным),
т.к. знак остатка принципиально
важен.
Составим систему Штурма для
заданного многочлена
1)
2)

остаток на 4 и берем его с противоположным
знаком.
Получим
3)

на 25, поменяем знак и получим:
4)

остаток на
обратную величину, поменяем знак и
получим:
Получили
систему Штурма:

знаки этих многочленов при и
при .
Конечно, вычислять тут ничего не нужно,
достаточно посмотреть только на
коэффициенты при старших степенях и на
сами эти степени. Например:

т.д. Занесем результаты выводов в таблицу:
|
|
|
|
|
|
Кол-во перемен знаков |
|
|
|
+ |
— |
+ |
— |
+ |
4 |
|
|
+ |
+ |
+ |
+ |
+ |
0 |
Вывод:
Многочлен имеет ровно действительных
корня.
Локализуем их. Для этого продолжим
таблицы, выбрав «на глазок» точки для
проверки знаков многочленов системы.
Первую точку нужно взять такой, чтобы
набор плюсов и минусов был одинаков
с ,
а последующие выгодны такие, при которых
количество перемен знаков изменяется,
причем таких перемен должно быть ровно
столько, сколько корней имеет многочлен.
|
|
|
|
|
|
Кол-во перемен знаков |
|
|
|
+ |
— |
+ |
— |
+ |
4 |
|
|
0 |
+ |
— |
— |
+ |
2 |
Замечание:
повезло, т.к. при получаем
,
т.е. —
корень многочлена. Мы не только
локализовали, но определили его точное
значение. Заметим, что количество перемен
знаков уменьшается на 2, т.е. на этом
интервале есть один корень, он дает одно
изменение, и корень в этой точке дает
еще одну перемену. Но продолжим.
|
|
|
|
|
|
Кол-во перемен знаков |
|
|
|
+ |
— |
— |
— |
+ |
2 |
|
|
— |
— |
— |
+ |
+ |
1 |
|
|
— |
— |
+ |
+ |
+ |
1 |
|
|
+ |
+ |
+ |
+ |
+ |
0 |
Вывод:
Про корни можно сказать:
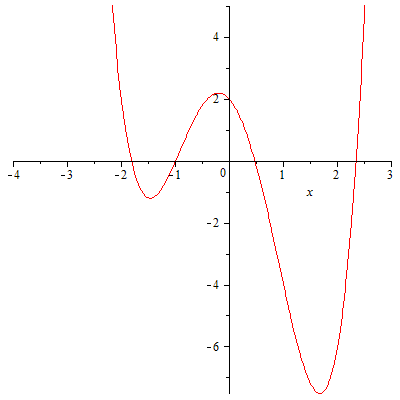
При
помощи компьютерных технологий можно
построить график функции и
убедиться в правильности рассуждений.
-
Розклад
многочлена по степенях
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Наибольший Общий Делитель (НОД)
На этом уроке мы узнаем, что такое НОД. Для более полного понимания этой темы, обязательно посмотрите предыдущий урок про делители и кратные.
Будем разбираться с самого простого примера.
Возьмем число 12. И найдем для начала все делители этого числа.
Число 12 имеет следующие делители: 12, 6, 4, 3, 2 и 1.
Теперь давайте найдем наибольший делитель числа 12. Тут все очень просто.
Наибольшим делителем любого натурального числа, является само это число
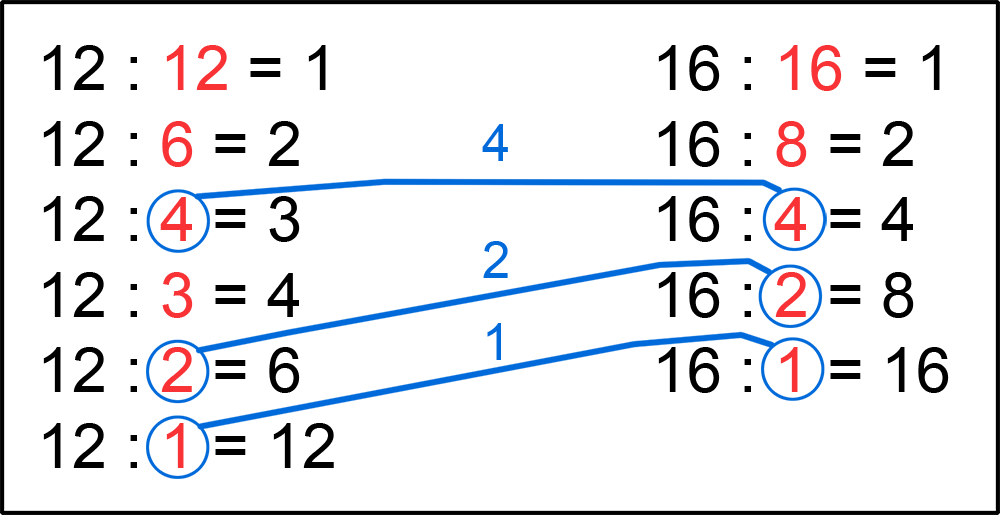
Усложним задачу. Найдем делители двух чисел. 12 и 16. Делители числа 12 мы уже знаем.
Число 16 имеет такие делители: 16, 8, 4, 2 и 1. Теперь давайте найдем общие делители этих двух чисел. Как мы видим, это числа: 4, 2 и 1.
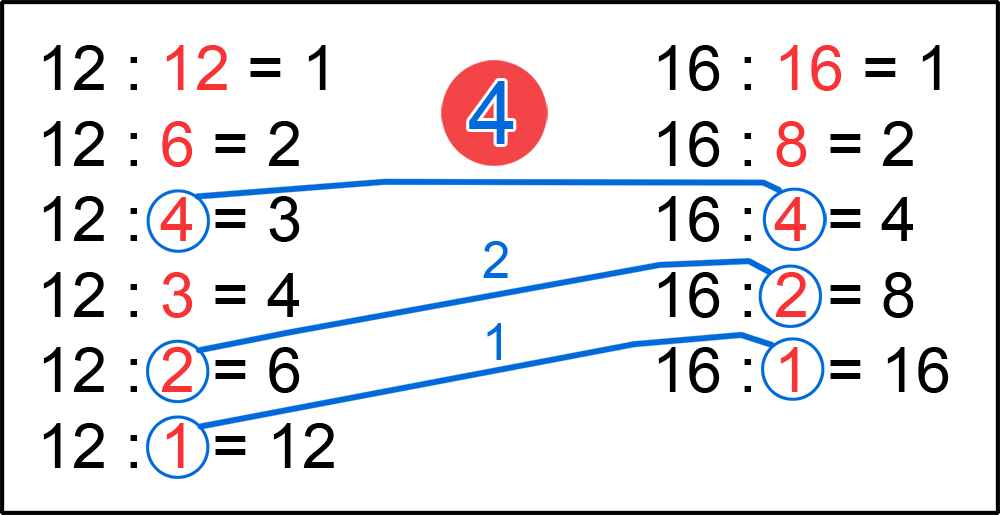
Нам осталось только найти Наибольший Общий Делитель чисел 12 и 16.
Наибольшим Общим Делителем будет число 4.
Наибольший Общий Делитель – это и есть НОД.
Записывается это таким способом.
НОД ( 12, 16 ) = 4 ( НОД чисел 12 и 16 равен четырем )
Теперь давайте еще больше усложним задачу.
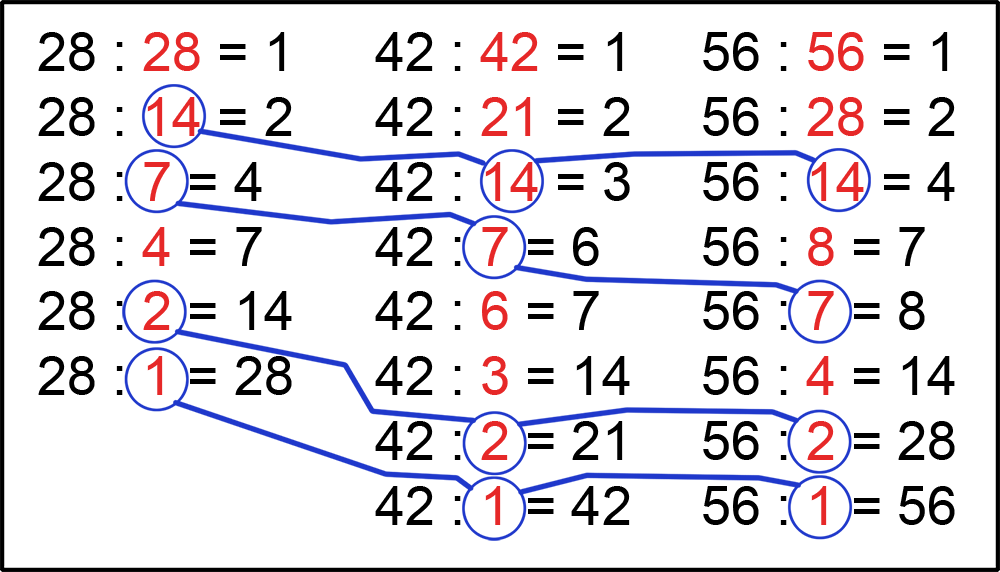
Найдем Наибольший Общий Делитель (НОД) уже трех чисел: 28, 42 и 56.
НОД ( 28, 42, 56 ) = ?
Найдем НОД по знакомому нам алгоритму.
Находим делители трех чисел. Далее ищем общие делители. И затем легко находим Наибольший Общий Делитель (НОД), это число 14.
НОД ( 28, 42, 56 ) = 14
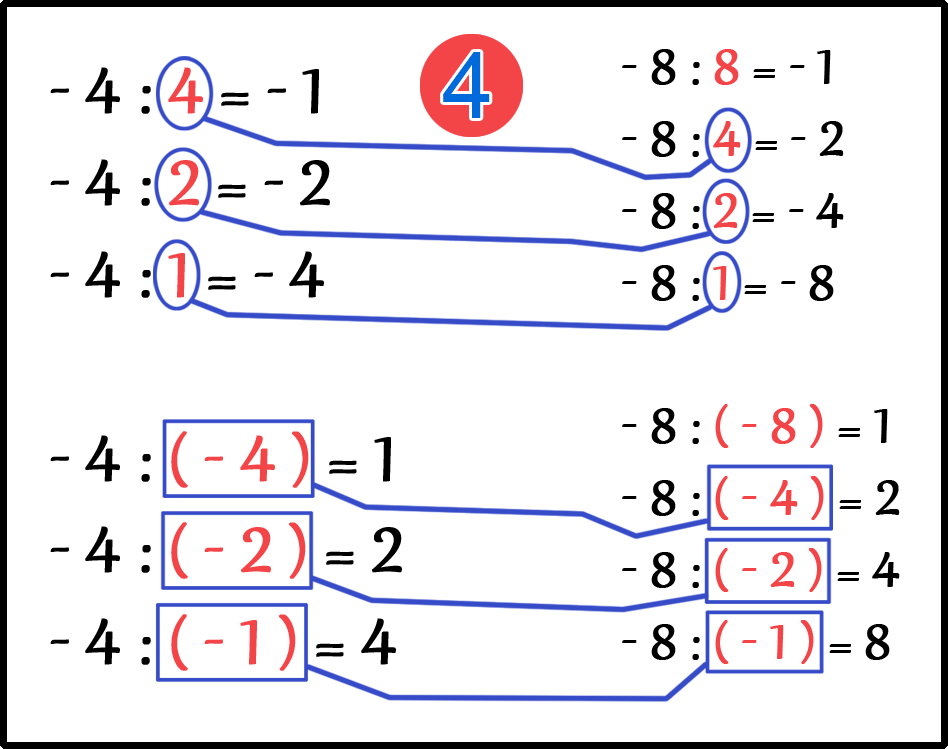
Далее попробуем найти НОД двух отрицательных чисел -4 и -8.
НОД ( -4, -8 ) = ?
И так, мы находим делители двух отрицательных чисел.
Теперь, находим общие делители.
И мы видим, что Наибольшим Общим Делителем (НОД) будет положительное число 4.
НОД ( -4, -8 ) = 4
Если бы эти отрицательные числа -4 и -8 были положительные, то Наибольший Общий Делитель (НОД) был бы такой же. Поэтому, если нам нужно будет найти НОД отрицательных чисел, мы просто можем считать их положительными.
НОД ( -4, -8 ) = 4
НОД ( 4, 8 ) = 4
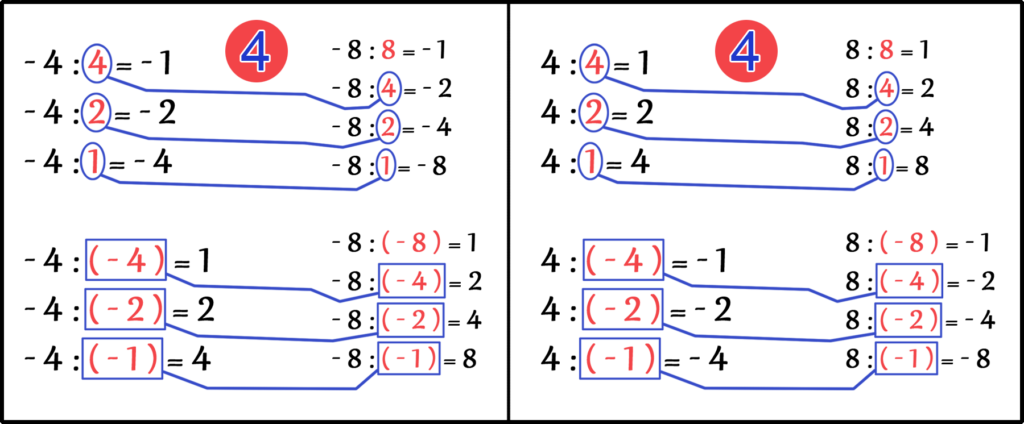
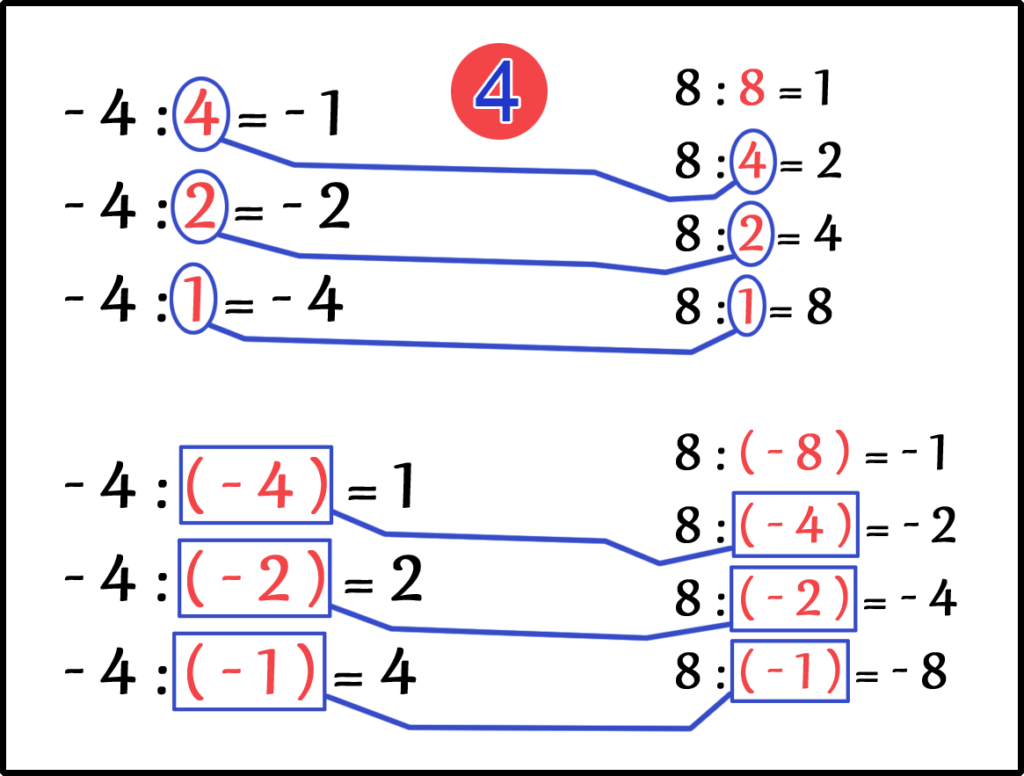
А если одно число будет положительное, а другое отрицательное?
Найдем Наибольший Общий Делитель (НОД) чисел -4 и 8.
И здесь мы тоже видим, что Наибольшим Общим Делителем (НОД) чисел -4 и 8 является число 4.
НОД ( -4, 8 ) = 4
Теперь мы понимаем, что
При нахождении Наибольшего Общего Делителя (НОД) мы можем игнорировать все отрицательные числа и считать их положительными
Мы научились находить НОД двух и более чисел. Но этот процесс занимает очень много времени. Можно даже и не говорить о нахождении НОД больших чисел, таких как например 200, 500 и так далее, это будет очень долго.
Чтобы упростить процесс нахождения Наибольшего Общего Делителя (НОД), были придуманы разные способы. Мы рассмотрим 2 способа.
Алгоритм Евклида
Алгоритм Евклида — эффективный алгоритм для нахождения наибольшего общего делителя двух чисел. Алгоритм назван в честь греческого математика Евклида (который жил в III веке до н. э.)
Это один из старейших численных алгоритмов, используемых в наше время.
Алгоритм Евклида работает только для двух чисел
Но есть хитрость, позволяющая находить и для более двух чисел, но об этом немного позже.
Вообще для Алгоритма Евклида нужен отдельный урок, так как тема очень интересная и сложная…
Но я постараюсь как можно сильнее все упростить, чтобы было проще понять.
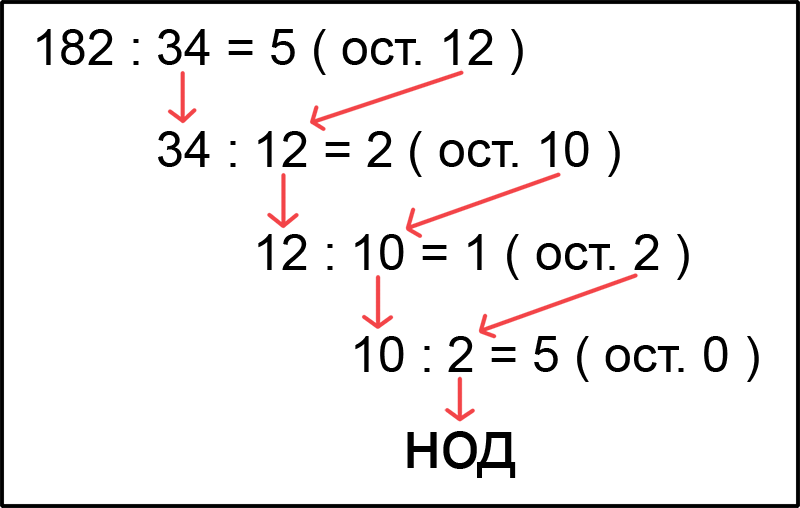
Найдем НОД ( 34, 182 ) используя Алгоритм Евклида.
Чтобы найти НОД двух чисел используя алгоритм Евклида, нам нужно большее число разделить на меньшее. Если ответ будет без остатка, то число на которое мы делили, то есть делитель и будет Наибольшим Общим Делителем (НОД), а если при делении большего числа на меньшее мы в ответе получим число с остатком, мы продолжаем деление, но теперь мы уже должны делитель разделить на остаток, и повторять это до тех пор, пока в остатке у нас не будет ноль. И тогда Наибольшим Общим Делителем (НОД) будет делитель. В нашем примере это число 2.
НОД ( 34, 182 ) = 2
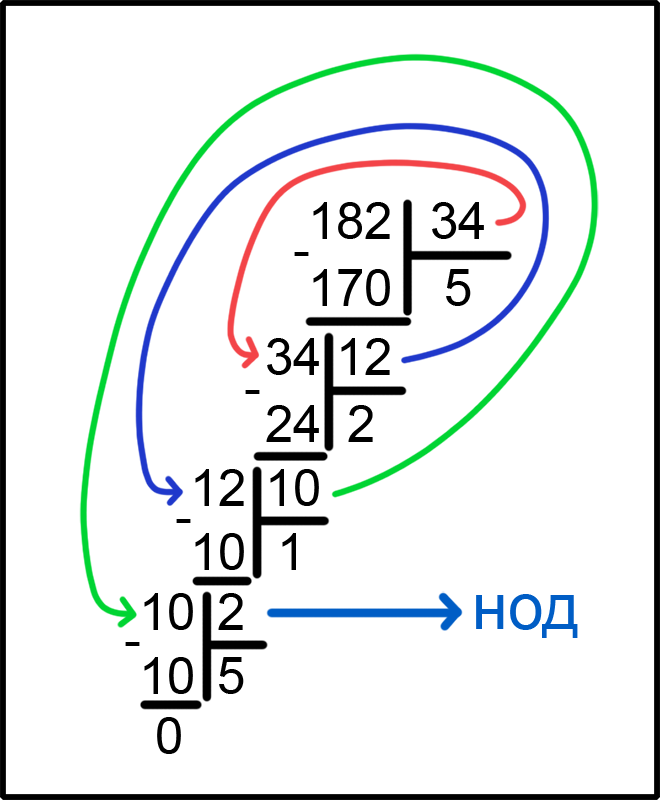
Это также можно записать другим способом. Делением в столбик. Производя операции деления до тех пор, пока в остатке не будет ноль.
И последнее число, на которое мы делим, и будет Наибольшим Общим Делителем (НОД), это число 2.
НОД ( 34, 182 ) = 2
А теперь давайте попробуем найди НОД уже не двух, а трех чисел с помощь Алгоритма Евклида.
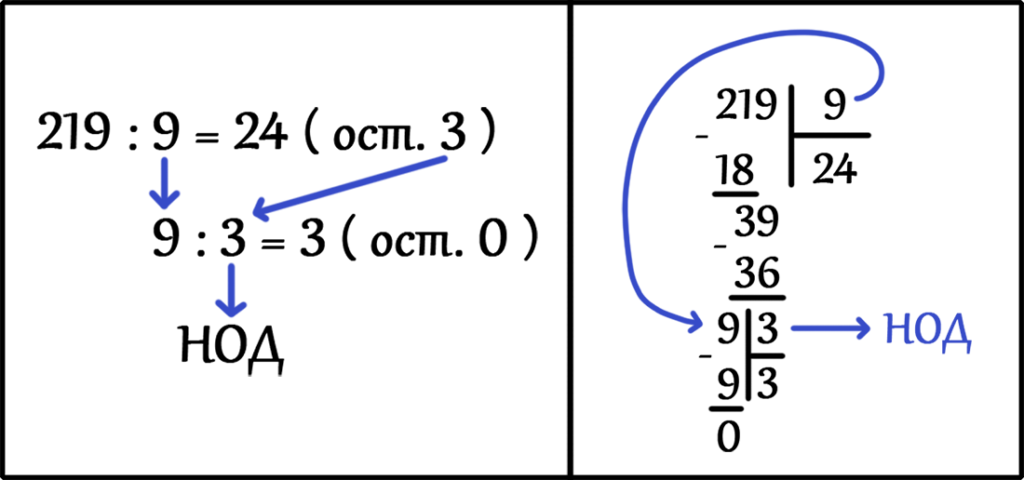
НОД ( 45, 153, 219 ) = ?
И вот здесь нам будет нужна одна хитрость, так как алгоритм создан для нахождения НОД только двух чисел. Здесь уже нужно будет проделать больше действий.
И так, у нас есть 3 числа: 45, 153 и 219. Мы из эти трех чисел возьмем любые 2 числа (в нашем случае это будут числа 45 и 153) и найдем Наибольший Общий Делитель (НОД) этих двух чисел при помощи алгоритма Евклида. Как это делать, мы с вами уже знаем.
НОД ( 45, 153 ) = ?
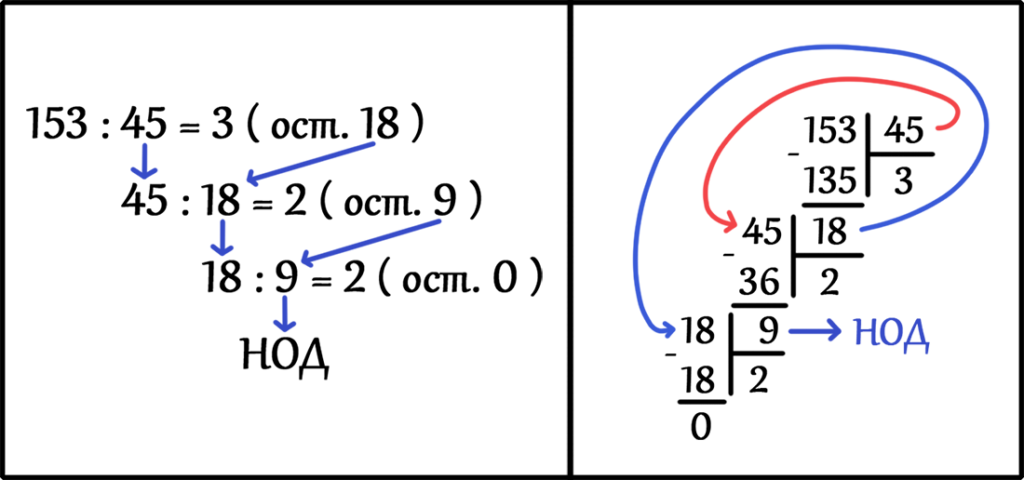
Большее число 153 делим на меньшее число 45 до тех пор, пока в остатке не будет ноль. Ответом будет делитель, число 9.
НОД ( 45, 153 ) = 9
И что нам теперь делать? У нас осталось только одно число 219. Теперь нам нужно найти НОД ( 9, 219 ) используя алгоритм Евклида.
НОД ( 9, 219 ) = ?
Проделываем те же самые действия.
НОД ( 45, 153, 219 ) = 3
Эти действия можно также проделывать для нахождения Наибольшего Общего Делителя (НОД) четырех и более чисел.
Разложение на простые множители
Как разложить число на простые множители мы знаем.
ссылка на Урок № 29 / Разложение чисел на простые множители.
Теперь давайте используем эти знания для нахождения Наибольшего Общего Делителя (НОД).
И так, найдем Наибольший Общий Делитель (НОД) двух чисел при помощи разложения на простые множители.
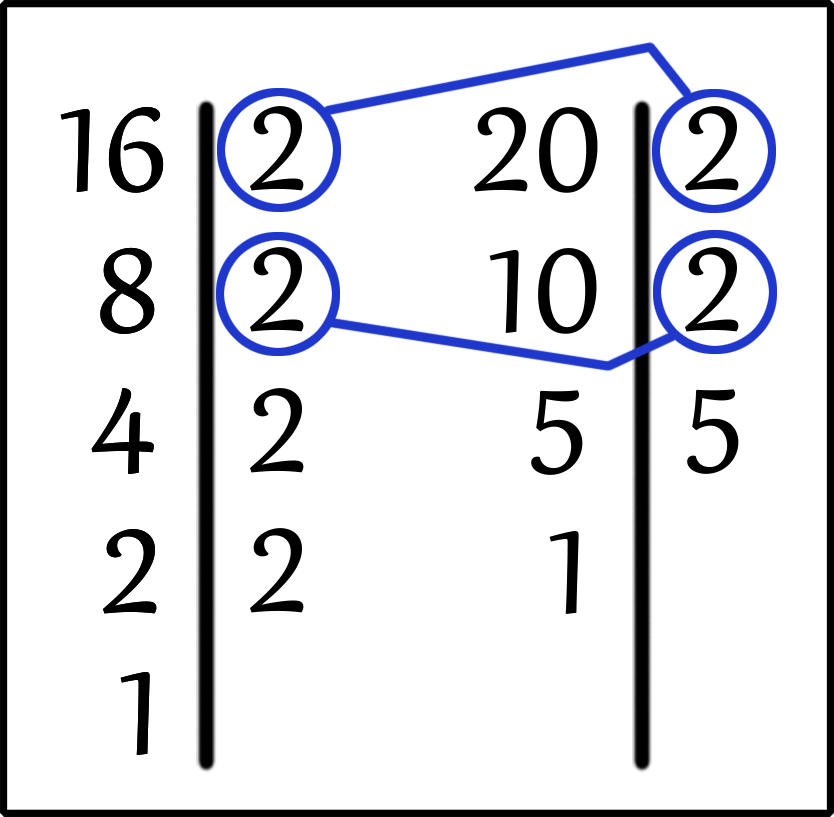
НОД ( 16, 20 ) = ?
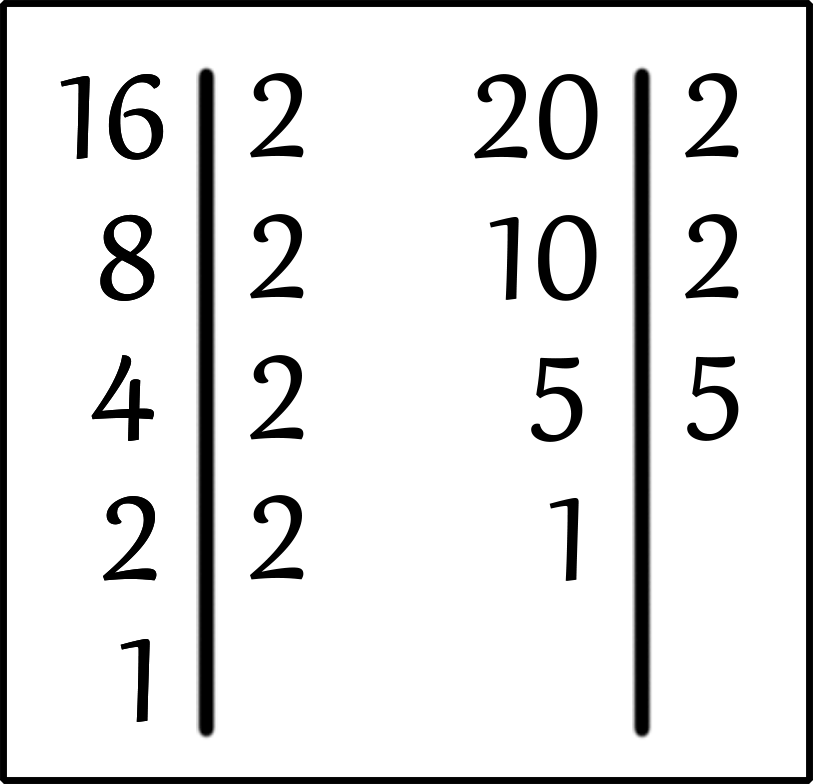
Раскладываем на простые множители два числа в столбик.
Число 16 раскладывается на простые множители:
Число 20 раскладывается на простые множители:
Что мы делаем дальше? Дальше мы находим одинаковые простые множители у чисел 16 и 20.
И находим две двойки.
Затем находим произведение одинаковых простых множителей.
Значит, Наибольшим Общим Делителем (НОД) чисел 16 и 20 будет число 4.
НОД ( 16, 20 ) = 4
Теперь давайте возьмем числа еще больше.
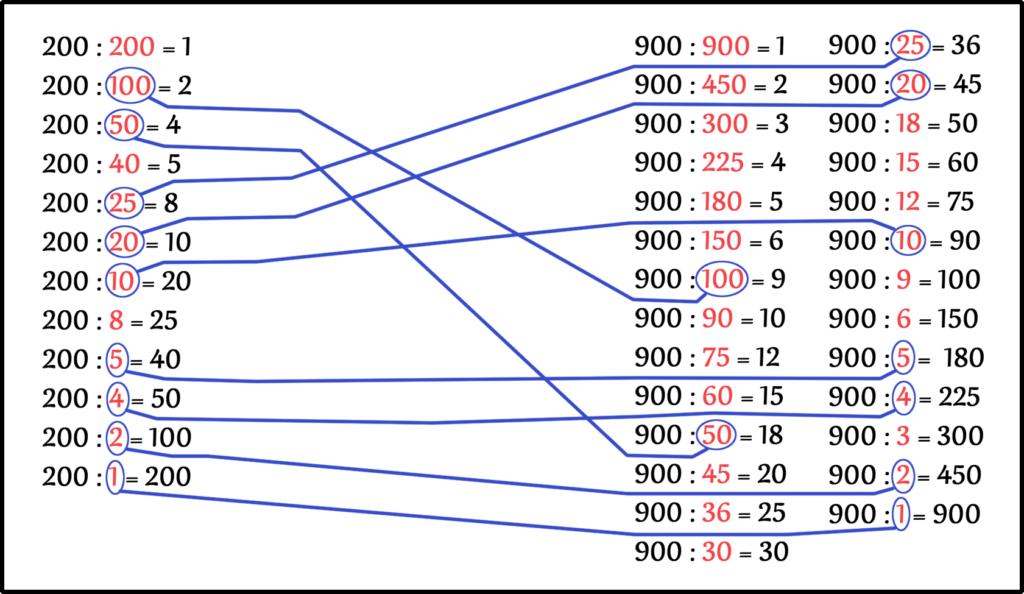
НОД ( 240, 900 ) = ?
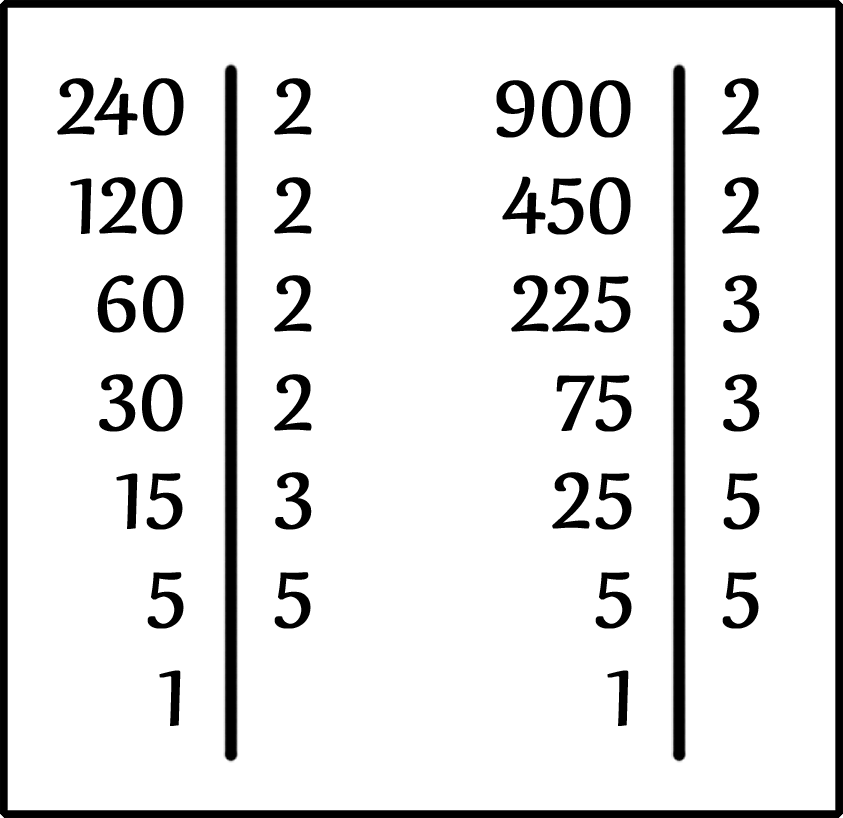
Раскладываем на простые множители два числа в столбик.
Число 240 раскладывается на простые множители:
Число 900 раскладывается на простые множители:
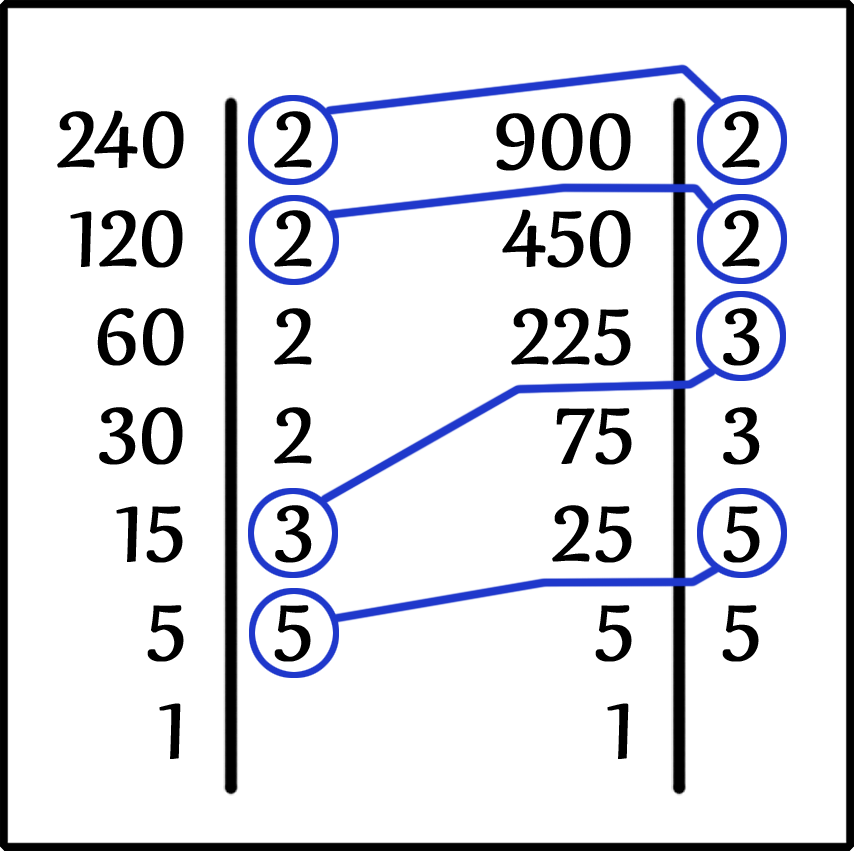
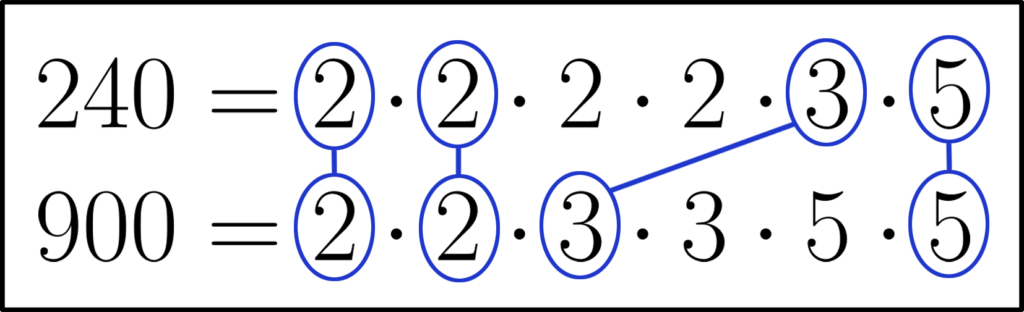
Теперь находим одинаковые простые множители.
Находим произведение одинаковых простых множителей.
Значит, Наибольшим Общим Делителем (НОД) чисел 240 и 900 будет число 60.
НОД ( 240, 900 ) = 60
Теперь для закрепления урока, решим несколько примеров.
Пример 1
При помощи алгоритма Евклида и разложения на простые множители найдите:
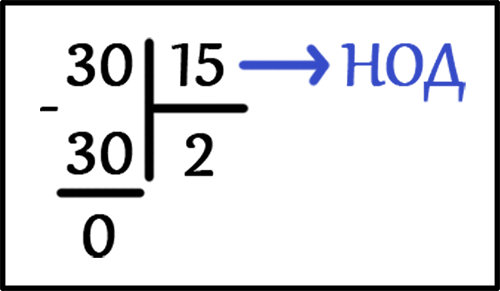
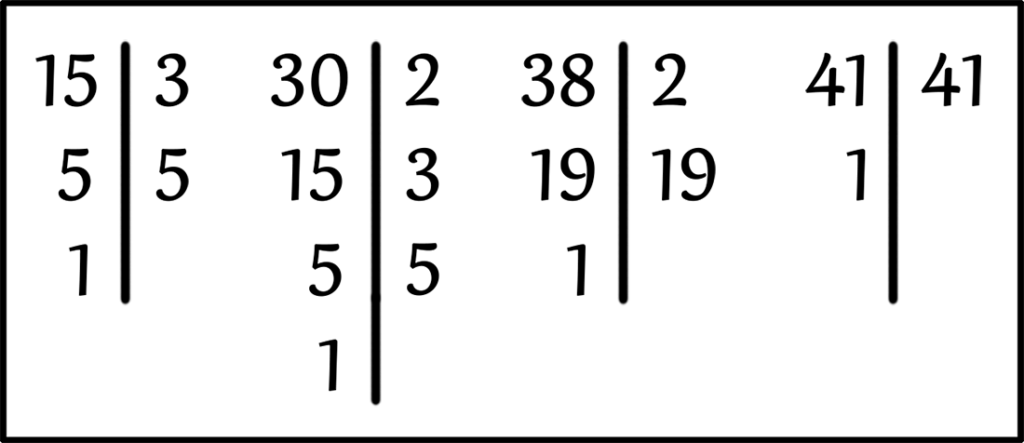
НОД ( 15, 30, 38, 41 ) = ?
Начнем с алгоритма Евклида.
Возьмем любые два числа, пускай это будут числа: 15 и 30.
НОД ( 15, 30 ) = ?
Разделим в столбик большее число 30 на меньшее число 15. Будем делить до тех пор, пока в остатке не будет ноль.
НОД ( 15, 30 ) = 15
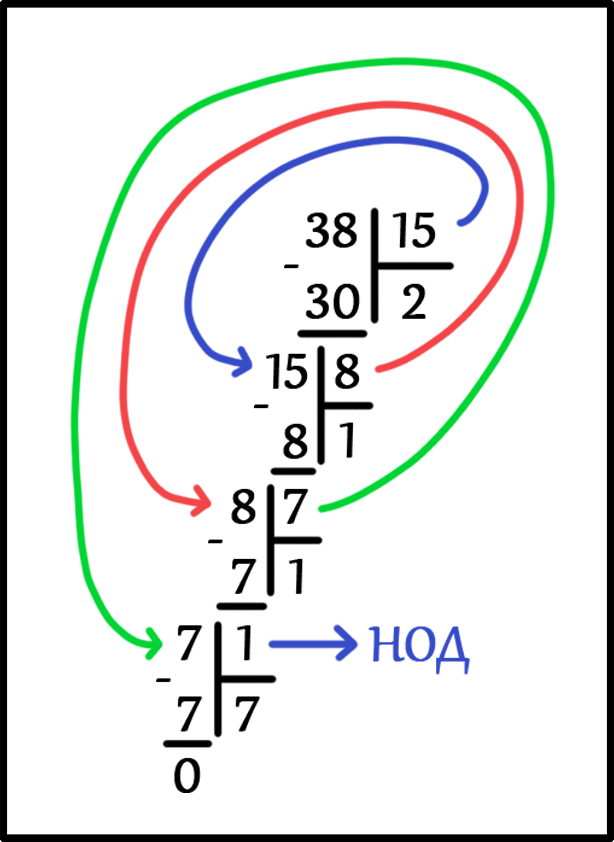
Далее берем другие два числа. Число 15 которое мы только что нашли и любое число из двух оставшихся. Пусть будет число 38.
НОД ( 15, 38 ) = ?
Разделим большее число 38 на меньшее число 15. Будем делить до тех пор, пока в остатке не будет ноль.
НОД ( 15, 38 ) = 1
И у нас осталось два числа, число 1 которое мы только что получили и число 41.
НОД ( 15, 30, 38, 41 )
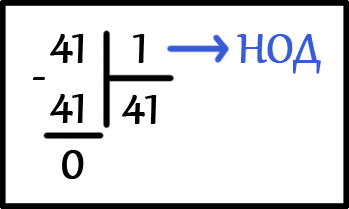
НОД ( 1, 41 ) = ?
Разделим большее число 41 на меньшее число 1. Будем делить до тех пор, пока в остатке не будет ноль.
НОД ( 1, 41 ) = 1
И в итоге Наибольший Общий Делитель (НОД) чисел 15, 30, 38 и 41 будет равен числу 1.
НОД ( 15, 30, 38, 41 ) = 1
Числа, которые не имеют никаких общих делителей, кроме единицы называются – взаимно простыми
То есть числа 15, 30, 38 и 41 – взаимно простые.
Теперь давайте найдем Наибольший Общий Делитель (НОД) чисел 15, 30, 38 и 41 при помощи разложения на простые множители.
НОД ( 15, 30, 38, 41 ) = ?
Раскладываем числа 15, 30, 38 и 41 на простые множители.
Число 41 – это простое число, а как мы с вами помним, разложением на простые множители простого числа является само простое число.
Теперь находим одинаковые простые множители и видим, что числа 15, 30, 38 и 41 делятся только на единицу.
НОД ( 15, 30, 38, 41 ) = 1
Пример 2
При помощи алгоритма Евклида и разложения на простые множители найдите:
НОД ( 24, 36, 54, 210 ) = ?
Начнем с алгоритма Евклида.
Возьмем любые два числа. Пускай это будут первые два числа.
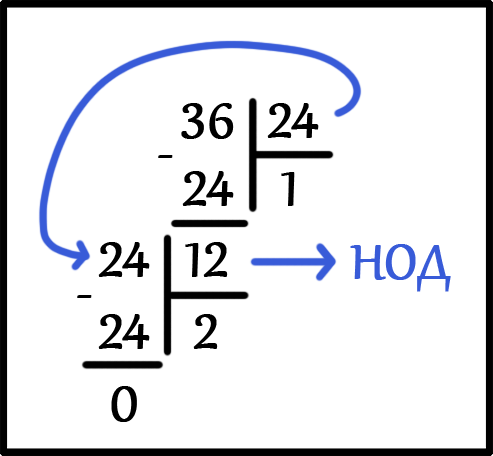
НОД ( 24, 36 ) = ?
Разделим в столбик большее число 36 на меньшее число 24. Будем делить до тех пор, пока в остатке не будет ноль.
НОД ( 24, 36 ) = 12
Далее берем другие два числа. Число 12 которое мы только что получили и любое число из двух оставшихся. Пусть будет число 54.
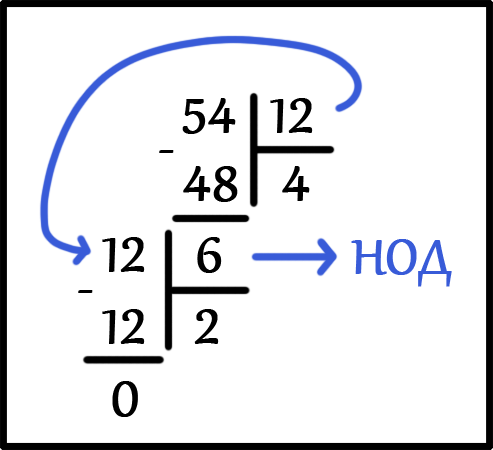
НОД ( 12, 54 ) = ?
Делим большее число 54 на меньшее число 12. Будем делить до тех пор, пока в остатке не будет ноль.
НОД ( 12, 54 ) = 6
И у нас осталось только два числа, число 6 которое мы только что получили и число 210.
НОД ( 24, 36, 54, 210 )
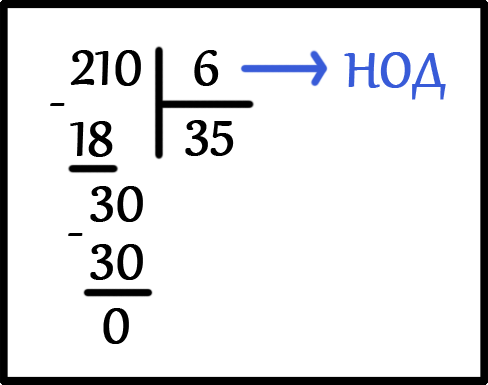
НОД ( 6, 210 ) = ?
Делим большее число 210 на меньшее число 6. Будем делить до тех пор, пока в остатке не будет ноль.
НОД ( 6, 210 ) = 6
И в итоге Наибольший Общий Делитель (НОД) чисел 24, 36, 54 и 210 будет равен числу 6.
НОД ( 24, 36, 54, 210 ) = 6
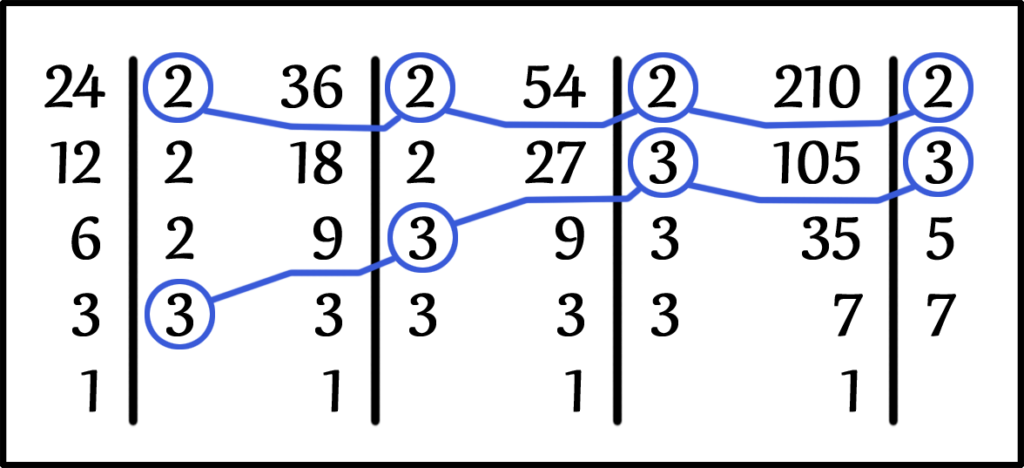
Теперь давайте найдем НОД чисел 24, 36, 54 и 210 при помощи разложения на простые множители.
НОД ( 24, 36, 54, 210 ) = ?
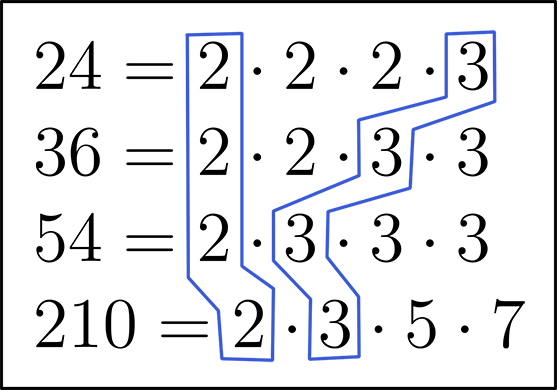
Раскладываем числа 15, 30, 38 и 41 на простые множители. И находим одинаковые простые множители.
Далее находим произведение одинаковых простых множителей.
Значит, Наибольшим Общим Делителем (НОД) чисел 24, 36, 54 и 210 будет число 6.
НОД ( 24, 36, 54, 210 ) = 6
И напоследок, давайте с вами решим одну задачу.
Задача
У нас есть: 72 груши, 96 яблок, 120 апельсин и 168 бананов. Какое максимальное кол-во ящиков нужно, чтобы в каждый положить одинаковое кол-во груш, яблок, апельсин и бананов? Сколько и какие фрукты лежат в каждом ящике? Какую часть из всех фруктов составляют Груши? Яблоки? Апельсины? Бананы?
Чтобы эту задачу проще понять, можно абстрагироваться от фруктов и ящиков и рассматривать только числа.
Тогда задача будет звучать так:
У нас есть 4 числа: 72, 96, 120 и 168. Нам нужно найти такое наибольшее число, на которое делятся данные числа без остатка. Я думаю вы уже поняли, как эту задачу нужно решать. Нам нужно найти Наибольший Общий Делитель (НОД) чисел: 72, 96, 120 и 168.
НОД ( 72, 96, 120, 168 ) = ?
Наибольшим Общим Делителем (НОД) чисел 72, 96, 120 и 168 будет число 24.
НОД ( 72, 96, 120, 168 ) = 24
Значит нам нужно 24 ящика, чтобы положить в них одинаковое количество фруктов.
Далее нам осталось узнать, сколько и какие фрукты лежат в каждом ящике.
Просто разделим фрукты на ящики.
72 (груши) : 24 (ящика) = 3 (груши в каждом ящике)
96 (яблок) : 24 (ящика) = 4 (яблока в каждом ящике)
120 (апельсин) : 24 (ящика) = 5 (апельсин в каждом ящике)
168 (бананов) : 24 (ящика) = 7 (бананов в каждом ящике)
И в итоге мы получаем, что в каждом ящике по 3 груши, 4 яблока, 5 апельсин и 7 бананов.
И нам осталось ответить на вопрос. Какую часть из всех фруктов составляют Груши? Яблоки? Апельсины? Бананы?
Здесь нам нужно вспомнить дроби.
Для начала узнаем сколько всего у нас фруктов.
Получается что у нас 456 разных фруктов.
И теперь мы можем легко узнать какую часть из всех фруктов составляют Груши? Яблоки? Апельсины? Бананы?
Домашние задания
1
Найдите все общие делители следующих чисел:
a) 11, 12
b) 14, 28
c) 10, 20, 35
d) 42, 63, 84, 105
2
Являются ли следующие числа взаимно простыми? (Да/Нет)
a) 1, 2
b) 22, 56
c) 34, 63
d) 115, 135, 189
e) 104, 147, 171
f) 148, 168, 280
g) 188, 224, 238, 294
3
Найдите НОД при помощи алгоритма Евклида следующих чисел:
a) НОД ( 14, 38 )
b) НОД ( 16, 80, 96 )
c) НОД ( 9, 24, 33 )
d) НОД ( 19, 21, 31, 45 )
e) НОД ( 104, 117, 143, 169 )
4
Найдите НОД при помощи разложения на простые множители следующих чисел:
a) НОД ( 12, 30 )
b) НОД ( 28, 36, 64 )
c) НОД ( 38, 95, 171 )
d) НОД ( 58, 68, 76, 94 )
e) НОД ( 132, 198, 231, 330 )
5
При каких значениях x, равенство будет верным? *
x – натуральное число.
НОД ( x, 12 ) = 12 – x
6
Чему равен x = ?, y = ?, b = ? *
Найдите НОД ( x, y, x + y, x – y) = b
17 + ( 193 – 2x ) ∙ 13 = 908 : 4 – ( 7 – 5 ∙ 14 : 2 ) + 87
14y – ( 9 ∙ 45 + 85 : 5 + 68 ) = 0
In the general theory of greatest common divisor we can define an element $d$ to be a greatest common divisor of $a$ and $b$ if
- $d$ divides both $a$ and $b$
- for all $c$, if $c$ divides both $a$ and $b$, then $c$ divides $d$.
If we stick to the natural numbers, we see that a unique greatest common divisor exists for all pairs of numbers.
The situation is more complicated when we try to extend the theory to arbitrary integral domains.
If we go to the integers, there are generally two. For instance, if $a=4$ and $b=6$, both $2$ and $-2$ satisfy the conditions above.
It’s even worse in the case of polynomials (say over the reals): if we consider $f(X)=X^2-3X+2$ and $g(X)=X^2-X$, then any polynomial of the form $a(X-1)$ (for a real $ane0$) satisfies the conditions for being a greatest common divisor.
What happens is that whenever $d$ is a greatest common divisor of $a$ and $b$ and $u$ is an invertible element, then also $ud$ is a greatest common divisor as well.
It’s however easy to show that, in an integral domain, if a greatest common divisor $d$ of $a$ and $b$ exists, then any other is of the form $ud$ for $u$ an invertible element.
In some cases we are able to add a further condition to guarantee uniqueness. For instance, in the integers we can impose that a greatest common divisor should be nonnegative; in the ring of polynomials over the reals (or any field), uniqueness is usually guaranteed by choosing the monic greatest common divisor (with the exception of the greatest common divisor of $0$ and $0$, which is of course $0$).
In the ring of Gaussian integers $mathbb{Z}[i]$ the invertible elements are $1$, $-1$, $i$ and $-i$ and there’s no sensible way to define a greatest common divisor so as to get some uniqueness.
As you see, it’s a matter of conventions. It’s better if we can add a condition that gives uniqueness, so we can define a bona fide operation, but actually it doesn’t really matter from the theoretical point of view.
Время на прочтение
8 мин
Количество просмотров 19K
Алгоритмы – одна из центральных тем в программировании, они повсюду (особенно на собеседованиях, ха-ха).
(Разве можно обойтись в таком посте без «баяна»?)
Одним из самых известных является так называемый алгоритм Евклида – пожалуй, самый распространенный способ нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел. С него также зачастую любят начинать изучение (и обучение) соответствующих разделов математики и информатики.
А Дональд Кнут, небезызвестный автор трактата “Искусство программирования” (и не только), и вовсе считает алгоритм первым в истории (по крайней мере, относительно современных определений). Потому что, не смотря на то, что алгоритм был придуман и использовался еще до, собственно, Евклида, который жил в IV-III вв. до нашей эры (он упоминается уже у Аристотеля, жившего веком ранее), Евклид описывает процесс итеративно, что согласуется с современным значением слова.
Само слово “алгоритм” восходит к имени персидского математика Аль-Хорезми, жившего примерно в VIII-IX вв. уже нашей эры. А началом его использования в смысле, близком современному, считается уже лишь XX век, точнее – его первые десятилетия, восход информационных технологий.
Алгоритм Евклида
Любопытства ради предлагаю ознакомиться с евклидовским описанием алгоритма в редактуре Кнута. Оно довольно длинное, поэтому спрятано под катом:
Описание алгоритма Евклида, близкое к исходному
Предложение. Для данных двух положительных целых чисел найти их наибольший общий делитель.
Пусть A и C – два заданных положительных целых числа; требуется найти их НОД. Если число A делится на C, то число C есть общий делитель чисел C и A, поскольку оно делит самое себя. И очевидно, что оно будет и наибольшим делителем, поскольку нет числа большего, чем число C, которое бы делило C.
Но если C не делит число A, то будем непрерывно вычитать меньшее из чисел A и C из большего до тех пор, пока не получим число, которое нацело делит предыдущее вычитаемое. Это должно рано или поздно произойти, потому что, если разность будет равна единице, то единица будет делить предыдущее вычитаемое.
Теперь положим, что E – положительный остаток от деления числа A на C; пусть F – положительный остаток от деления числа C на число E и пусть F делит E. Так как F делит E, а E делит C — F, F также делит C — F. Но оно делит и самое себя, поэтому F делит C, а C делит A — E; поэтому F делит также A — E, но оно делит и E; поэтому F делит A. Следовательно F является общим делителем чисел A и C.
Теперь я утверждаю, что оно является и НОД. Действительно, если F – не наибольший общий делитель чисел A и C, то найдется большее число, которое будет делить оба этих числа. Пусть таким числом будет G.
Так как число G делит число C, а число C – делит A — E, то G также делит число A — E. Число G делит также все число A, поэтому оно делит и остаток E. Но E делит C — F, поэтому G также делит C — F. А число G также делит все число C, так как оно делит и остаток F; таким образом, большее число делит меньшее, а это невозможно.
Таким образом, нет такого числа, большего, чем F, которое бы делило A и C; значит, число F является НОД.
Следствие. Это рассуждение делает очевидным предположение, что всякое число, делящее два числа, делит и их НОД. Ч.т.д.
Описание приводит два способа нахождения НОД – вычитанием и делением. Собственно, и в наши дни широко известны эти два способа реализации алгоритма.
Вот пример функции, написанной на «Swift», реализации первого способа:
func subtractionGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
while firstNumber != 0, secondNumber != 0 {
if firstNumber > secondNumber {
firstNumber = firstNumber - secondNumber
} else {
secondNumber = secondNumber - firstNumber
}
}
return firstNumber + secondNumber // One of them is 0.
}Здесь, переиспользования ради, я вынес в отдельную функцию случаи поиска НОД, когда он известен сразу, без необходимости следования какому-либо алгоритму:
func simpleCasesGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int? {
if firstNumber == secondNumber {
return firstNumber // Any.
}
if firstNumber == 0 {
return secondNumber
}
if secondNumber == 0 {
return firstNumber
}
return nil
}(Если два числа равны, то, естественно, их НОД также равен им. Если какое-то из чисел равно нулю, то НОД будет равняться второму числу, т.к. ноль делится любым числом (с результатом, понятное дело, тоже ноль).)
В качестве входных данных могут использоваться только неотрицательные значения. Соответственно, для отрицательных можно использовать те же методы, но взяв числа по модулю. (Да, общий делитель может быть и отрицательным, но мы ищем именно НОД, а положительные числа, очевидно, всегда больше отрицательных.)
А вот так может выглядеть реализация версии алгоритма делением:
func divisionGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
while firstNumber != 0, secondNumber != 0 {
if firstNumber > secondNumber {
firstNumber = firstNumber % secondNumber
} else {
secondNumber = secondNumber % firstNumber
}
}
return firstNumber + secondNumber // One of them is 0.
}Вторая версия в наши дни считается предпочтительней, так как содержит в себе, в среднем, ощутимо меньшее количество шагов. Тем не менее, во времена, когда компьютеры были большие и медленные, операция деления могла быть сама по себе сложной процедурой. И тогда первая версия алгоритма могла оказаться эффективней.
Чтобы немного их сравнить, я произвел несколько замеров с использованием любимого мной метода measure(_:) класса XCTestCase «нативного» фреймворка для тестирования кода в Xcode-проектах XCTest.
В качестве входных данных я использовал массив пар случайных чисел. Замеры производились, естественно, с использованием одного и того же массива для каждого способа. Разброс чисел для пар я взял от нуля до 9999. Замеры производились на количестве вычислений (пар чисел): одно, десять, 100, 1000, 10000, 100000, 1000000 и 10000000. Последнее заставляло ожидать результата уже несколько минут, поэтому на нем я решил остановиться.
Вот простой код генерации входных данных:
let pairs = (0..<100).map { _ in (Int.random(in: 0..<10000), Int.random(in: 0..<10000)) } // Generates 100 pairs.Сам замер выглядит, например, так:
func testSubstractionGCDPerformance() {
measure() {
_ = pairs.map { substractionGCD($0, $1) }
}
}А вот так выглядят результаты запуска на моем компьютере:
(Subtraction – вычитание, division – деление.)
В общем, очень хорошо видно, как сильно на современных компьютерах проигрывает метод вычитания.
«Улучшенная» версия алгоритма Евклида
В литературе можно встретить версию алгоритма, в которой одно из чисел на каждом шаге вместо остатка от деления на второе заменяется на разность между этим отстатком и вторым числом, но только в случае, если остаток от деления больше половины второго числа. Реализация этой версии может выглядеть так:
func improvedDivisionGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
while firstNumber != 0, secondNumber != 0 {
if firstNumber > secondNumber {
let firstNumberClaim = firstNumber % secondNumber
if firstNumberClaim > secondNumber / 2 {
firstNumber = abs(firstNumberClaim - secondNumber)
} else {
firstNumber = firstNumberClaim
}
} else {
let secondNumberClaim = secondNumber % firstNumber
if secondNumberClaim > firstNumber / 2 {
secondNumber = abs(secondNumberClaim - firstNumber)
} else {
secondNumber = secondNumberClaim
}
}
}
return firstNumber + secondNumber // One of them is 0.
}Такая модификация сокращает количество шагов алгоритма, но, судя по результатам замеров на моем компьютере, дополнительные вычисления и проверки на каждом шаге, нейтрализуют это преимущество и даже более:
(Improved – «улучшенная» версия.)
Еще немного о значимости алгоритма Евклида
Алгоритм имеет также геометрическую версию (для нахождения наибольшей меры двух отрезков).
Алгоритм был, конечно, обощен и для нахождения НОД любого количества чисел, не только двух. В двух словах идея такова: если обозначить функцию поиска НОД двух чисел как gcd(a, b), то, скажем, НОД трех чисел gcd(a, b, c) равен gcd(gcd(a, b), c). И так далее, для любого количества чисел НОД находится последовательным вычислением НОД НОД-а предыдущей пары чисел и следующего числа. Хотя, конечно, это касается поиска НОД вообще, а не только алгоритма Евклида.
Существует также обощение алгоритма для нахождения НОД полиномов. Но это уже выходит за рамки этого несложного поста, а в некоторой степени, и моих познаний в математике.
Сложность алгоритма Евклида
Временная сложность алгоритма исследовалась давно, не быстро и гораздо более учеными мужами, чем ваш покорный слуга. Тем не менее, вопрос давно закрыт и ответ получен. Собственно, еще в середине позапрошлого века. Габриэлем Ламе.
Если коротко, то ответ формулируется, собственно, теоремой Ламе, связанной с этим алгоритмом. Количество шагов алгоритма будет равно порядковому номеру ближайшего большего числа Фибоначчи наименьшему из двух чисел входных параметров минус 2. Оперируя чуть более традиционно-математическими обозначениями, то если u > v (и v > 1), то число проходов алгоритма будет равняться n — 2 при v < Fn (Fn – это некое ближайшее v число Фибоначчи, а n – это его порядковый номер).
Числа Фибоначчи растут экспоненциально, соответственно, имеем логарифмическую функцию времени выполнения алгоритма (от меньшего из двух входных чисел).
Те же самые выкладки показывают, что наихужшие для алгоритма входные данные – это два последовательных числа Фибоначчи.
Бинарный метод поиска НОД
Говоря о поиске НОД, стоит быть упомянутым алгоритм, предложенный уже в 60-е годы прошлого столетия неким Джозефом Стейном, о котором я не нашел в Сети вообще никакой информации. Он (алгоритм) ориентирован на двоичную арифметику и не содержит операций деления. Алгоритм оперирует только проверками четности и делением пополам, что осуществимо возможностями одной лишь бинарной арифметики.
Алгоритм основывается на четырех фактах:
- Если u и v оба четны, то gcd(u, v) = 2 * gcd(u / 2, v / 2);
- Если u четно, а v – нет, gcd(u, v) = gcd(u / 2, v);
- gcd(u, v) = gcd(u — v, v) (это следует из алгоритма Евклида);
- Если u и v оба нечетны, то u — v – четно и |u — v| < max(u, v)
На «Wikipedia» можно посмотреть рекурсивную версию алгоритма (на современных языках программирования записывается в несколько строк), я не стал ее переписывать на «Swift». А здесь я приведу вариант итеративной реализации:
func binaryGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
var shift = 0
while (firstNumber | secondNumber) & 1 == 0 {
shift += 1
firstNumber >>= 1
secondNumber >>= 1
}
while firstNumber & 1 == 0 {
firstNumber >>= 1
}
repeat {
while secondNumber & 1 == 0 {
secondNumber >>= 1
}
if firstNumber > secondNumber {
swap(&firstNumber, &secondNumber)
}
secondNumber -= firstNumber
} while secondNumber != 0
return firstNumber << shift
}Сделав замеры на тех же данных, к сожалению, этот мудреный алгоритм на моем компьютере не оправдал возложенных на него надежд. Конечно, он все еще работает в два раза быстрее евклидова алогоритма вычитанием, но заметно уступает классической его версии с делением. Полная таблица сводных данных:
(Binary – бинарный алгоритм.)
(Не исключаю, что алгоритм можно записать более эффективно, чем это сделал я, и это повлияет на результат, но на что же нам тогда нужны компиляторы?!)
Кстати, этот алгоритм, безусловно, получивший свои 15 минут славы уже в век информационных технологий (в более раннюю его часть, чем текущая), был известен еще в Древнем Китае. Его описание обнаружено в трудах, датируемых I в. н.э. Конечно, в терминах вроде «половинного деления» и вычитания. А также в контексте сокращения дробей.
Заключение
Честно говоря, этим простеньким «исследованием» я не собирался ничего доказывать и не хотел делать какие-то революционные умозаключения (и ведь не сделал же!). Я всего лишь хотел удовлетворить свое любопытство, посмотреть на работу разных подходов для решения классической задачи и слегка размять пальцы. Тем не менее, я надеюсь, наблюдать результаты было любопытно и вам!
Альтернативные алгоритмы вычисления НОД и НОК. Алгоритм Евклида
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Шарапов К.А. 1
1МБОУ «Гимназия № 41» г.Кемерово
Ломонова О.А. 1
1МБОУ «Гимназия № 41» г.Кемерово
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
С понятиями наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) учащиеся средней школы, встречаются в шестом классе. Данная тема всегда трудна для усвоения. Дети часто путают эти понятия, не понимают, зачем их нужно изучать. В последнее время и в научно-популярной литературе встречаются отдельные высказывания о том, что данный материал нужно исключить из школьной программы. Думаю, что это не совсем верно, и изучать его нужно если не на уроках, то во внеурочное время на занятиях школьного компонента обязательно, так как это способствует развитию логического мышления школьников, повышению скорости вычислительных операций, умению решать задачи красивыми методами.
Данная работа знакомит с алгоритмами вычисления НОД. Знакомство с ними не только дополняет и углубляет знания, но и развивает интерес к предмету, любознательность и логическое мышление. Предлагаемая работа рассчитана на учеников, желающих повысить уровень математической подготовки, увидеть красоту математических выкладок и эстетику алгоритма Евклида, а так же помочь учащимся не бояться громоздких и очень трудных с виду задач с НОД, помня пословицу: «Волков бояться, в лес не ходить!».
Гипотеза: Если алгоритм Евклида является удобным и быстрым способом вычисления НОД, то нужно знакомить с ним учащихся и чаще использовать.
Цель исследования: изучить разные алгоритмы вычисления НОД, выявить наиболее рациональные способы решения, красиво и сравнительно просто приводящие к ответу.
Достижение поставленной цели требует решения следующих основных задач:
Рассмотреть несколько алгоритмов вычисления НОД
Сравнить алгоритмы вычисления НОД
Провести анкетирование
Составить список рекомендаций
Предмет исследования: Алгоритмы вычисления НОД
Объект исследования: умения и навыки вычисления НОД
Методы исследования:
Изучение специальной литературы по данному вопросу: энциклопедии, справочники и учебные пособия.
Анкетирование.
Сравнение и анализ.
Обработка полученных данных (составление обобщающих таблиц, диаграмм)
Работа в компьютерных программах Microsoft Word, Excel, Microsoft PowerPoint
Глава 1. «Прадедушка» всех алгоритмов
Алгоритм Евклида — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел. Алгоритм назван в честь греческого математика Евклида, который впервые описал его в VII и X книгах «Начал».
В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары.
Первое описание алгоритма находится в «Началах Евклида» (около 300 лет до н. э.), что делает его одним из старейших численных алгоритмов, используемых в наше время. Оригинальный алгоритм был предложен только для натуральных чисел и геометрических длин (вещественных чисел). Однако в 19 веке он был обобщён на другие типы чисел, такие как целые числа Гаусса и полиномы от одной переменной. Это привело к появлению в современной общей алгебре такого понятия, как «Евклидово кольцо». Позже алгоритм Евклида также был обобщен на другие математические структуры, такие как узлы и многомерные полиномы.
Долгое время алгоритм Евклида был самым эффективным способом отыскания наибольшего общего делителя, однако с появлением электронно-вычислительных машин ситуация изменилась (алгоритм Евклида, как нетрудно понять, появился задолго до вычислительных машин). Учет специфических особенностей выполнения арифметических операций компьютером позволил построить более эффективную (для программной реализации) версию алгоритма Евклида.
Глава 2. Алгоритмы вычисления НОД
2.1 Алгоритм простого перебора
Чтобы найти наибольший общий делитель двух данных натуральных чисел можно действовать по определению: выписать все делители этих чисел, выделить среди них общие и выбрать среди всех общих делителей наибольший.
Пример.
Найдем все делители чисел 54 и 36.
54 делится на 1; 2; 3; 6; 9; 18; 27; 54.
36 делится на 1; 2; 3; 4; 6; 9; 18; 36.
Общими делителями являются числа: 1, 2, 3, 6, 9, 18.
Значит НОД(54; 36)=18
2.2 Нахождение НОД с помощью разложения чисел на простые множители
Рассмотрим еще один способ нахождения НОД. Наибольший общий делитель может быть найден по разложениям чисел на простые множители.
Сформулируем правило: НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители.
Приведем пример для пояснения правила нахождения НОД.
Пусть нам известны разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими простыми множителями, участвующими в разложении чисел 220 и 600, являются 2, 2 и 5. Следовательно, НОД(220, 600)=2·2·5=20.
Таким образом, если разложить числа a и b на простые множители и найти произведение всех их общих множителей, то будет найден наибольший общий делитель чисел a и b.
Пример.
Найдите наибольший общий делитель чисел 72 и 96.
Решение.
Разложим числа 72 и 96 на простые множители.
72=2·2·2·3·3 и 96=2·2·2·2·2·3. Общими простыми множителями являются 2, 2, 2 и 3. Таким образом, НОД(72, 96)=2·2·2·3=24.
Ответ: НОД(72, 96)=24.
В заключение этого пункта заметим, что справедливость приведенного правила нахождения НОД следует из свойства наибольшего общего делителя, которое утверждает, что НОД(m·a, m·b)=m·НОД(a, b), где m – любое целое положительное число.
2.3. Алгоритм Евклида
Одним из простейших алгоритмов нахождения наибольшего общего делителя является Алгоритм Евклида. Он может быть реализован, как при помощи вычитания, так и деления. Рассмотрим каждый из этих двух способов.
а) Описание алгоритма нахождения НОД вычитанием:
Из большего числа вычитаем меньшее.
Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
Переходим к пункту 1.
Пример:
Найти НОД для 42 и 18.
42 — 18 = 24
24 – 18 = 6
18 — 6 = 12
12 – 6 = 6
6-6=0
Конец: НОД – это уменьшаемое или вычитаемое. НОД (42, 18)=6
б) Описание алгоритма нахождения НОД делением:
Большее число делим на меньшее. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
Если есть остаток, то большее число заменяем на остаток от деления.
Переходим к пункту 1.
Пример.
Пусть требуется найти НОД(102;84). Разделим одно число на другое и определим остаток.
102=84*1+18 0 <18<84
Теперь проделаем такую же операцию для чисел 84 и 18:
84=18*4+ 12 0 <12<18
Следующий шаг — для 18 и 12:
18=12*1+6 0 <6<12
Теперь — для 12 и 6:
12=6*2+0 0-остаток. Процесс закончился.
2.4. Бинарный алгоритм Евклида.
Бинарный алгоритм вычисления наибольшего общего делителя, как понятно из названия, находит наибольший общий делитель двух целых чисел. В сравнении с хорошо известным алгоритмом Евклида, этот на практике работает быстрее, но в тоже время немного уступает первому в простоте реализации. Алгоритм был известен еще в Китае 1-го века, но опубликован был лишь в 1967 году, израильским физиком и программистом Джозефом Стайном. Он основан на использовании следующих свойств НОД:
НОД(2n, 2m) = 2 НОД(n, m)
НОД(2n, 2m+1) = НОД(n, 2m+1)
НОД(-n, m) = НОД(n, m)
2.5. Нахождение НОД трех и большего количества чисел
Нахождение наибольшего общего делителя трех и большего количества чисел может быть сведено к последовательному нахождению НОД двух чисел. Теорема: наибольший общий делитель нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3,
НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.
Давайте разберемся, как выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.
Пример.
Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.
Решение. В этом примере a1=78, a2=294, a3=570, a4=36.
Сначала по алгоритму Евклида определим наибольший общий делитель d2 двух первых чисел 78 и 294. При делении получаем равенства 294=78·3+60; 78=60·1+18; 60=18·3+6 и 18=6·3. Таким образом, d2=НОД(78, 294)=6.
Теперь вычислим d3=НОД(d2, a3)=НОД(6, 570). Опять применим алгоритм Евклида: 570=6·95, следовательно, d3=НОД(6, 570)=6.
Осталось вычислить d4=НОД(d3, a4)=НОД(6, 36). Так как 36 делится на 6, то d4=НОД(6, 36)=6.
Таким образом, наибольший общий делитель четырех данных чисел равен d4=6, то есть,
НОД(78, 294, 570, 36)=6.
Ответ: НОД(78, 294, 570, 36)=6.
Разложение чисел на простые множители также позволяет вычислять НОД трех и большего количества чисел. В этом случае наибольший общий делитель находится как произведение всех общих простых множителей данных чисел.
Пример.
Вычислите НОД чисел из предыдущего примера, используя их разложения на простые множители.
Решение.
Разложим числа 78, 294, 570 и 36 на простые множители, получаем 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3. Общими простыми множителями всех данных четырех чисел являются числа 2 и 3. Следовательно, НОД(78, 294, 570, 36)=2·3=6.
Ответ: НОД(78, 294, 570, 36)=6.
2.6. Нахождение НОД отрицательных чисел
Если одно, несколько или все числа, наибольший делитель которых нужно найти, являются отрицательными числами, то их НОД равен наибольшему общему делителю модулей этих чисел. Это связано с тем, что противоположные числа a и −a имеют одинаковые делители.
Пример.
Найдите НОД отрицательных целых чисел −231 и −140.
Решение.
Модуль числа −231 равен 231, а модуль числа −140 равен 140, и НОД(−231, −140) = НОД(231, 140). Алгоритм Евклида дает нам следующие равенства: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Следовательно, НОД(231, 140)=7. Тогда искомый наибольший общий делитель отрицательных чисел −231 и −140 равен 7.
Ответ: НОД(−231, −140)=7.
Пример.
Определите НОД трех чисел −585, 81 и −189.
Решение.
При нахождении наибольшего общего делителя отрицательные числа можно заменить их абсолютными величинами, то есть, НОД(−585, 81, −189)=НОД(585, 81, 189). Разложения чисел 585, 81 и 189 на простые множители имеют соответственно вид 585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими простыми множителями этих трех чисел являются 3 и 3. Тогда НОД(585, 81, 189)=3·3=9, следовательно, НОД(−585, 81, −189)=9.
Ответ: НОД(−585, 81, −189)=9.
Глава 3 Оценка эффективности применения алгоритмов
3.1. Сравнение алгоритмов Евклида вычитанием и делением.
Возьмем два числа: 112 и 32. Первое больше второго – присвоим ему остаток от деления 112 на 32. Теперь у нас имеются числа 16 и 32. Второе больше, поэтому присвоим ему остаток отделения 32 на 16, т. е. 0. Так выглядят эти действия в виде таблицы:
Начальные данные 112 32
Шаг 1 16 32
Шаг 2 16 0
А теперь снова, используя те же самые числа, составим таблицу, но на этот раз при помощи алгоритма вычитания.
Начальные данные 112 32
Шаг 1 80 32
Шаг 2 48 32
Шаг 3 16 32
Шаг 4 16 0
Из примера видно, что Алгоритм Евклида, реализуемый делением эффективней метода вычитания.
3.2. Сравнение алгоритмов вычисления НОД
Сравним алгоритмы вычисления НОД на двух примерах:
I. Сколько шагов потребуется, чтобы вычислить НОД (1980; 390)
1) алгоритм простого перебора – 360 шагов
2) алгоритм разложения на простые множители – 14 шагов
3) бинарный алгоритм Евклида – 4 шага
4) алгоритм Евклида – 2 шага
II. Найти НОД (20451; 3065)
1) алгоритм простого перебора – 6018 шагов
2) алгоритм разложения на простые множители – 25 шагов
3) бинарный алгоритм Евклида – 7 шагов
4) алгоритм Евклида – 7 шагов
Чтобы убедится в преимуществе приема последовательного деления над приемами разложения на простые множители, когда имеем дело с большими числами, рассмотрим следующий пример. Найти НОД (4847, 4181).
Разложение данных чисел на простые множители является делом нелегким, так как ни одно из чисел 2, 3, 4, 5, 6, 9, для которых устанавливаются в школе признаки делимости, не является делителем данных чисел. Алгоритм же Евклида легко и быстро приводит к результату: НОД (4847, 4181) = НОД(4181,666)=НОД(666,185)=НОД(185,111)=
НОД(111,74)=НОД(74,37)=37
Другой пример: сократить дробь
Решение. Выполним деление с остатком. Разделим 833 на 714:
833:714= 1(остаток 119)
Здесь делимое а = 833, делитель в = 714 и остаток r = 119.
НОД (833,714) = НОД (714, 119). Теперь разделим 714 :119=6, остаток 0. Таким образом, НОД (833 и 714) = 119. Тогда = .
Проведенное анкетирование показало, что большинство учителей знают алгоритм Евклида и знакомят учащихся с ним только на факультативах.
Список рекомендаций:
Нахождение НОД с помощью алгоритма Евклида не входит в общеобразовательную программу по математике, однако этот способ отыскания НОД следует показать в классе с преобладающим числом мотивированных учащихся.
Показать эффективность использования различных алгоритмов вычисления НОД чисел, из которых каждый ученик может выбрать те, которые показались ему целесообразными, и применять их на практике.
Полезно помнить, что НОД любого количества чисел не превосходит наименьшего из них.
Заключение.
В процессе проделанной работы в соответствии с ее целями и задачами были получены следующие выводы и результаты:
Для поиска НОД натуральных чисел существуют различные алгоритмы:
Если данные числа сравнительно невелики, то лучший алгоритм – непосредственный перебор.
Если числа достаточно большие, то нахождение НОД(а;b) путем перечисления всех делителей чисел а и b — процесс трудоемкий и ненадежный и тогда НОД(а;b) находится с помощью разложения чисел на простые множители. Этот алгоритм наиболее распространенный.
Алгоритм отыскания НОД(а, b) с помощью разложения чисел на простые множители прост, понятен и удобен, но у него есть существенный недостаток: если данные числа велики, да еще не очень легко раскладываются на множители, то задача отыскания НОД(а, b) становится довольно трудной. К тому же может оказаться, что, основательно потрудившись, мы убедимся, что НОД (а, b)=1 и вроде вся работа проделана зря.
Большинство древних алгоритмов со временем вытеснялось из вычислительной практики более новыми алгоритмами. Алгоритм Евклида избежал этой участи прежде всего благодаря своей экономности. Тем более удивительно, что хотя почтенный алгоритм Евклида и применяется в течение столь многих столетий, он не всегда является наилучшим способом для нахождения НОД!
Основной вывод, который мы сделали, состоит в том, что научиться быстро и правильно вычислять НОД чисел не так уж сложно. Вышеперечисленные алгоритмы рассчитаны на ум «обычного» человека и не требуют уникальных способностей. Главное — более или менее продолжительная тренировка.
В своей работе мы попытались показать эффективность использования различных алгоритмов вычисления НОД чисел, из которых каждый ученик может выбрать те, которые показались ему целесообразными, и применять их на практике. В будущем мы планируем продолжить исследование по данной теме и рассмотреть алгоритм Евклида для многочленов, при решении уравнений в целых числах.
Литература
[1].//Учебник для общеобразовательных учреждений Математика 6 класс под ред. Н.Я Зубаревой., Москва, Мнемозина,2013 г.
[2].//За страницами учебника алгебры. Л.Ф Пичурин, Москва, Просвещение, 1990г.
[3].//Сборник примеров и задач по математике, Н.А Терешин, Т.Н.Терешина Москва, Аквариум, 1997 г.
Интернет-ресурсы.
[1]. //Википедия (свободная энциклопедия), http://ru.wikipedia.org
[ 2]. //Сайт «Единая коллекция цифровых образовательных ресурсов».
[ 3]. // bymath.net — сайт «Вся элементарная математика», раздел «Общий делитель. Наибольший общий делитель»
Просмотров работы: 303