Как найти НОД
- Нахождение путём разложения на множители
- Алгоритм Евклида
Рассмотрим два способа нахождения наибольшего общего делителя.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.
Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.
Пример 1. Найти НОД (84, 90).
Решение: Раскладываем числа 84 и 90 на простые множители:
Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой:
2 · 3 = 6.
Таким образом, НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
Решение: Раскладываем 15 и 28 на простые множители:
Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.
НОД (15, 28) = 1.
Алгоритм Евклида
Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.
Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.
Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.
Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно:
НОД (27, 9) = 9.
В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:
- Из двух данных чисел большее число делят на меньшее.
- Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
- Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
- Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
- Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.
Пример 2. Найдём наибольший общий делитель чисел 140 и 96:
1) 140 : 96 = 1 (остаток 44)
2) 96 : 44 = 2 (остаток 
3) 44 : 8 = 5 (остаток 4)
4) 8 : 4 = 2
Последний делитель равен 4 — это значит:
НОД (140, 96) = 4.
Последовательное деление так же можно записывать столбиком:
Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
- Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
- Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
- Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.
Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа — 48:
48 : 4 = 12
48 делится на 4 без остатка. Таким образом:
НОД (140, 96, 48) = 4.
Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.
Как найти НОД?
Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
- выбрать одинаковые множители, входящие в оба разложения;
- найти их произведение.
Примеры нахождения наибольшего общего делителя
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОД 12 и 8
1. Раскладываем 12 и 8 на простые множители:
2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2
3. Перемножаем эти множители и получаем: 2 · 2 = 4
Ответ: НОД (8; 12) = 2 · 2 = 4.
Пример 2: найти НОД 75 и 150
Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:
1. Раскладываем 75 и 150 на простые множители:
2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5
3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75
Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.
Частный случай или взаимно простые числа
Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:
Пример 3: найти НОД 9 и 5
1. Раскладываем 5 и 9 на простые множители:
Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted 

In the name «greatest common divisor», the adjective «greatest» may be replaced by «highest», and the word «divisor» may be replaced by «factor», so that other names include highest common factor (hcf), etc.[3][4][5][6] Historically, other names for the same concept have included greatest common measure.[7]
This notion can be extended to polynomials (see Polynomial greatest common divisor) and other commutative rings (see § In commutative rings below).
Overview[edit]
Definition[edit]
The greatest common divisor (GCD) of two nonzero integers a and b is the greatest positive integer d such that d is a divisor of both a and b; that is, there are integers e and f such that a = de and b = df, and d is the largest such integer. The GCD of a and b is generally denoted gcd(a, b).[8]
This definition also applies when one of a and b is zero. In this case, the GCD is the absolute value of the non zero integer: gcd(a, 0) = gcd(0, a) = |a|. This case is important as the terminating step of the Euclidean algorithm.
The above definition cannot be used for defining gcd(0, 0), since 0 × n = 0, and zero thus has no greatest divisor. However, zero is its own greatest divisor if greatest is understood in the context of the divisibility relation, so gcd(0, 0) is commonly defined as 0. This preserves the usual identities for GCD, and in particular Bézout’s identity, namely that gcd(a, b) generates the same ideal as {a, b}.[9][10][11] This convention is followed by many computer algebra systems.[12] Nonetheless, some authors leave gcd(0, 0) undefined.[13]
The GCD of a and b is their greatest positive common divisor in the preorder relation of divisibility. This means that the common divisors of a and b are exactly the divisors of their GCD. This is commonly proved by using either Euclid’s lemma, the fundamental theorem of arithmetic, or the Euclidean algorithm. This is the meaning of «greatest» that is used for the generalizations of the concept of GCD.
Example[edit]
The number 54 can be expressed as a product of two integers in several different ways:
Thus the complete list of divisors of 54 is 
Similarly, the divisors of 24 are 
The numbers that these two lists have in common are the common divisors of 54 and 24, that is,
Of these, the greatest is 6, so it is the greatest common divisor:
Computing all divisors of the two numbers in this way is usually not efficient, especially for large numbers that have many divisors. Much more efficient methods are described in § Calculation.
Coprime numbers[edit]
Two numbers are called relatively prime, or coprime, if their greatest common divisor equals 1.[14] For example, 9 and 28 are coprime.
A geometric view[edit]
A 24-by-60 rectangle is covered with ten 12-by-12 square tiles, where 12 is the GCD of 24 and 60. More generally, an a-by-b rectangle can be covered with square tiles of side length c only if c is a common divisor of a and b.
For example, a 24-by-60 rectangular area can be divided into a grid of: 1-by-1 squares, 2-by-2 squares, 3-by-3 squares, 4-by-4 squares, 6-by-6 squares or 12-by-12 squares. Therefore, 12 is the greatest common divisor of 24 and 60. A 24-by-60 rectangular area can thus be divided into a grid of 12-by-12 squares, with two squares along one edge (24/12 = 2) and five squares along the other (60/12 = 5).
Applications[edit]
Reducing fractions[edit]
The greatest common divisor is useful for reducing fractions to the lowest terms.[15] For example, gcd(42, 56) = 14, therefore,
Least common multiple[edit]
The least common multiple of two integers that are not both zero can be computed from their greatest common divisor, by using the relation
Calculation[edit]
Using prime factorizations[edit]
Greatest common divisors can be computed by determining the prime factorizations of the two numbers and comparing factors. For example, to compute gcd(48, 180), we find the prime factorizations 48 = 24 · 31 and 180 = 22 · 32 · 51; the GCD is then 2min(4,2) · 3min(1,2) · 5min(0,1) = 22 · 31 · 50 = 12 The corresponding LCM is then
2max(4,2) · 3max(1,2) · 5max(0,1) =
24 · 32 · 51 = 720.
In practice, this method is only feasible for small numbers, as computing prime factorizations takes too long.
Euclid’s algorithm[edit]
The method introduced by Euclid for computing greatest common divisors is based on the fact that, given two positive integers a and b such that a > b, the common divisors of a and b are the same as the common divisors of a – b and b.
So, Euclid’s method for computing the greatest common divisor of two positive integers consists of replacing the larger number by the difference of the numbers, and repeating this until the two numbers are equal: that is their greatest common divisor.
For example, to compute gcd(48,18), one proceeds as follows:
So gcd(48, 18) = 6.
This method can be very slow if one number is much larger than the other. So, the variant that follows is generally preferred.
Euclidean algorithm[edit]
Animation showing an application of the Euclidean algorithm to find the greatest common divisor of 62 and 36, which is 2.
A more efficient method is the Euclidean algorithm, a variant in which the difference of the two numbers a and b is replaced by the remainder of the Euclidean division (also called division with remainder) of a by b.
Denoting this remainder as a mod b, the algorithm replaces (a, b) by (b, a mod b) repeatedly until the pair is (d, 0), where d is the greatest common divisor.
For example, to compute gcd(48,18), the computation is as follows:
This again gives gcd(48, 18) = 6.
Lehmer’s GCD algorithm[edit]
Lehmer’s algorithm is based on the observation that the initial quotients produced by Euclid’s algorithm can be determined based on only the first few digits; this is useful for numbers that are larger than a computer word. In essence, one extracts initial digits, typically forming one or two computer words, and runs Euclid’s algorithms on these smaller numbers, as long as it is guaranteed that the quotients are the same with those that would be obtained with the original numbers. The quotients are collected into a small 2-by-2 transformation matrix (a matrix of single-word integers) to reduce the original numbers. This process is repeated until numbers are small enough that the binary algorithm (see below) is more efficient.
This algorithm improves speed, because it reduces the number of operations on very large numbers, and can use hardware arithmetic for most operations. In fact, most of the quotients are very small, so a fair number of steps of the Euclidean algorithm can be collected in a 2-by-2 matrix of single-word integers. When Lehmer’s algorithm encounters a quotient that is too large, it must fall back to one iteration of Euclidean algorithm, with a Euclidean division of large numbers.
Binary GCD algorithm[edit]
The binary GCD algorithm uses only subtraction and division by 2.
The method is as follows: Let a and b be the two non-negative integers. Let the integer d be 0. There are five possibilities:
- a = b.
As gcd(a, a) = a, the desired GCD is a × 2d (as a and b are changed in the other cases, and d records the number of times that a and b have been both divided by 2 in the next step, the GCD of the initial pair is the product of a and 2d).
- Both a and b are even.
Then 2 is a common divisor. Divide both a and b by 2, increment d by 1 to record the number of times 2 is a common divisor and continue.
- a is even and b is odd.
Then 2 is not a common divisor. Divide a by 2 and continue.
- a is odd and b is even.
Then 2 is not a common divisor. Divide b by 2 and continue.
- Both a and b are odd.
As gcd(a,b) = gcd(b,a), if a < b then exchange a and b. The number c = a − b is positive and smaller than a. Any number that divides a and b must also divide c so every common divisor of a and b is also a common divisor of b and c. Similarly, a = b + c and every common divisor of b and c is also a common divisor of a and b. So the two pairs (a, b) and (b, c) have the same common divisors, and thus gcd(a,b) = gcd(b,c). Moreover, as a and b are both odd, c is even, the process can be continued with the pair (a, b) replaced by the smaller numbers (c/2, b) without changing the GCD.
Each of the above steps reduces at least one of a and b while leaving them non-negative and so can only be repeated a finite number of times. Thus eventually the process results in a = b, the stopping case. Then the GCD is a × 2d.
Example: (a, b, d) = (48, 18, 0) → (24, 9, 1) → (12, 9, 1) → (6, 9, 1) → (3, 9, 1) → (3, 3, 1) ; the original GCD is thus the product 6 of 2d = 21 and a= b= 3.
The binary GCD algorithm is particularly easy to implement on binary computers. Its computational complexity is
The computational complexity is usually given in terms of the length n of the input. Here, this length is 
.
Other methods[edit]

If a and b are both nonzero, the greatest common divisor of a and b can be computed by using least common multiple (LCM) of a and b:
,
but more commonly the LCM is computed from the GCD.
Using Thomae’s function f,
which generalizes to a and b rational numbers or commensurable real numbers.
Keith Slavin has shown that for odd a ≥ 1:
which is a function that can be evaluated for complex b.[16] Wolfgang Schramm has shown that
is an entire function in the variable b for all positive integers a where cd(k) is Ramanujan’s sum.[17]
Complexity[edit]
The computational complexity of the computation of greatest common divisors has been widely studied.[18] If one uses the Euclidean algorithm and the elementary algorithms for multiplication and division, the computation of the greatest common divisor of two integers of at most n bits is 
However, if a fast multiplication algorithm is used, one may modify the Euclidean algorithm for improving the complexity, but the computation of a greatest common divisor becomes slower than the multiplication. More precisely, if the multiplication of two integers of n bits takes a time of T(n), then the fastest known algorithm for greatest common divisor has a complexity 

Previous complexities are valid for the usual models of computation, specifically multitape Turing machines and random-access machines.
The computation of the greatest common divisors belongs thus to the class of problems solvable in quasilinear time. A fortiori, the corresponding decision problem belongs to the class P of problems solvable in polynomial time. The GCD problem is not known to be in NC, and so there is no known way to parallelize it efficiently; nor is it known to be P-complete, which would imply that it is unlikely to be possible to efficiently parallelize GCD computation. Shallcross et al. showed that a related problem (EUGCD, determining the remainder sequence arising during the Euclidean algorithm) is NC-equivalent to the problem of integer linear programming with two variables; if either problem is in NC or is P-complete, the other is as well.[19] Since NC contains NL, it is also unknown whether a space-efficient algorithm for computing the GCD exists, even for nondeterministic Turing machines.
Although the problem is not known to be in NC, parallel algorithms asymptotically faster than the Euclidean algorithm exist; the fastest known deterministic algorithm is by Chor and Goldreich, which (in the CRCW-PRAM model) can solve the problem in O(n/log n) time with n1+ε processors.[20] Randomized algorithms can solve the problem in O((log n)2) time on 
Properties[edit]
- Every common divisor of a and b is a divisor of gcd(a, b).
- gcd(a, b), where a and b are not both zero, may be defined alternatively and equivalently as the smallest positive integer d which can be written in the form d = a⋅p + b⋅q, where p and q are integers. This expression is called Bézout’s identity. Numbers p and q like this can be computed with the extended Euclidean algorithm.
- gcd(a, 0) = |a|, for a ≠ 0, since any number is a divisor of 0, and the greatest divisor of a is |a|.[2][5] This is usually used as the base case in the Euclidean algorithm.
- If a divides the product b⋅c, and gcd(a, b) = d, then a/d divides c.
- If m is a positive integer, then gcd(m⋅a, m⋅b) = m⋅gcd(a, b).
- If m is any integer, then gcd(a + m⋅b, b) = gcd(a, b). Equivalently, gcd(a mod b,b) = gcd(a,b).
- If m is a positive common divisor of a and b, then gcd(a/m, b/m) = gcd(a, b)/m.
- The GCD is a commutative function: gcd(a, b) = gcd(b, a).
- The GCD is an associative function: gcd(a, gcd(b, c)) = gcd(gcd(a, b), c). Thus gcd(a, b, c, …) can be used to denote the GCD of multiple arguments.
- The GCD is a multiplicative function in the following sense: if a1 and a2 are relatively prime, then gcd(a1⋅a2, b) = gcd(a1, b)⋅gcd(a2, b).
- gcd(a, b) is closely related to the least common multiple lcm(a, b): we have
- gcd(a, b)⋅lcm(a, b) = |a⋅b|.
- This formula is often used to compute least common multiples: one first computes the GCD with Euclid’s algorithm and then divides the product of the given numbers by their GCD.
- The following versions of distributivity hold true:
- gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))
- lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c)).
- If we have the unique prime factorizations of a = p1e1 p2e2 ⋅⋅⋅ pmem and b = p1f1 p2f2 ⋅⋅⋅ pmfm where ei ≥ 0 and fi ≥ 0, then the GCD of a and b is
- gcd(a,b) = p1min(e1,f1) p2min(e2,f2) ⋅⋅⋅ pmmin(em,fm).
- It is sometimes useful to define gcd(0, 0) = 0 and lcm(0, 0) = 0 because then the natural numbers become a complete distributive lattice with GCD as meet and LCM as join operation.[22] This extension of the definition is also compatible with the generalization for commutative rings given below.
- In a Cartesian coordinate system, gcd(a, b) can be interpreted as the number of segments between points with integral coordinates on the straight line segment joining the points (0, 0) and (a, b).
- For non-negative integers a and b, where a and b are not both zero, provable by considering the Euclidean algorithm in base n:[23]
- gcd(na − 1, nb − 1) = ngcd(a,b) − 1.
- An identity involving Euler’s totient function:
where
is the p-adic valuation.
Probabilities and expected value[edit]
In 1972, James E. Nymann showed that k integers, chosen independently and uniformly from {1, …, n}, are coprime with probability 1/ζ(k) as n goes to infinity, where ζ refers to the Riemann zeta function.[24] (See coprime for a derivation.) This result was extended in 1987 to show that the probability that k random integers have greatest common divisor d is d−k/ζ(k).[25]
Using this information, the expected value of the greatest common divisor function can be seen (informally) to not exist when k = 2. In this case the probability that the GCD equals d is d−2/ζ(2), and since ζ(2) = π2/6 we have
This last summation is the harmonic series, which diverges. However, when k ≥ 3, the expected value is well-defined, and by the above argument, it is
For k = 3, this is approximately equal to 1.3684. For k = 4, it is approximately 1.1106.
In commutative rings[edit]
The notion of greatest common divisor can more generally be defined for elements of an arbitrary commutative ring, although in general there need not exist one for every pair of elements.
If R is a commutative ring, and a and b are in R, then an element d of R is called a common divisor of a and b if it divides both a and b (that is, if there are elements x and y in R such that d·x = a and d·y = b).
If d is a common divisor of a and b, and every common divisor of a and b divides d, then d is called a greatest common divisor of a and b.
With this definition, two elements a and b may very well have several greatest common divisors, or none at all. If R is an integral domain then any two GCD’s of a and b must be associate elements, since by definition either one must divide the other; indeed if a GCD exists, any one of its associates is a GCD as well. Existence of a GCD is not assured in arbitrary integral domains. However, if R is a unique factorization domain, then any two elements have a GCD, and more generally this is true in GCD domains.
If R is a Euclidean domain in which euclidean division is given algorithmically (as is the case for instance when R = F[X] where F is a field, or when R is the ring of Gaussian integers), then greatest common divisors can be computed using a form of the Euclidean algorithm based on the division procedure.
The following is an example of an integral domain with two elements that do not have a GCD:
The elements 2 and 1 + √−3 are two maximal common divisors (that is, any common divisor which is a multiple of 2 is associated to 2, the same holds for 1 + √−3, but they are not associated, so there is no greatest common divisor of a and b.
Corresponding to the Bézout property we may, in any commutative ring, consider the collection of elements of the form pa + qb, where p and q range over the ring. This is the ideal generated by a and b, and is denoted simply (a, b). In a ring all of whose ideals are principal (a principal ideal domain or PID), this ideal will be identical with the set of multiples of some ring element d; then this d is a greatest common divisor of a and b. But the ideal (a, b) can be useful even when there is no greatest common divisor of a and b. (Indeed, Ernst Kummer used this ideal as a replacement for a GCD in his treatment of Fermat’s Last Theorem, although he envisioned it as the set of multiples of some hypothetical, or ideal, ring element d, whence the ring-theoretic term.)
See also[edit]
- Bézout domain
- Lowest common denominator
- Unitary divisor
Notes[edit]
- ^ a b Long (1972, p. 33)
- ^ a b c Pettofrezzo & Byrkit (1970, p. 34)
- ^ Kelley, W. Michael (2004), The Complete Idiot’s Guide to Algebra, Penguin, p. 142, ISBN 978-1-59257-161-1.
- ^ Jones, Allyn (1999), Whole Numbers, Decimals, Percentages and Fractions Year 7, Pascal Press, p. 16, ISBN 978-1-86441-378-6.
- ^ a b c Hardy & Wright (1979, p. 20)
- ^ Some authors treat greatest common denominator as synonymous with greatest common divisor. This contradicts the common meaning of the words that are used, as denominator refers to fractions, and two fractions do not have any greatest common denominator (if two fractions have the same denominator, one obtains a greater common denominator by multiplying all numerators and denominators by the same integer).
- ^ Barlow, Peter; Peacock, George; Lardner, Dionysius; Airy, Sir George Biddell; Hamilton, H. P.; Levy, A.; De Morgan, Augustus; Mosley, Henry (1847), Encyclopaedia of Pure Mathematics, R. Griffin and Co., p. 589.
- ^ Some authors use (a, b),[1][2][5] but this notation is often ambiguous. Andrews (1994, p. 16) explains this as: «Many authors write (a,b) for g.c.d.(a, b). We do not, because we shall often use (a,b) to represent a point in the Euclidean plane.»
- ^ Thomas H. Cormen, et al., Introduction to Algorithms (2nd edition, 2001) ISBN 0262032937, p. 852
- ^ Bernard L. Johnston, Fred Richman, Numbers and Symmetry: An Introduction to Algebra ISBN 084930301X, p. 38
- ^ Martyn R. Dixon, et al., An Introduction to Essential Algebraic Structures ISBN 1118497759, p. 59
- ^ e.g., Wolfram Alpha calculation and Maxima
- ^ Jonathan Katz, Yehuda Lindell, Introduction to Modern Cryptography ISBN 1351133012, 2020, section 9.1.1, p. 45
- ^ Weisstein, Eric W. «Greatest Common Divisor». mathworld.wolfram.com. Retrieved 2020-08-30.
- ^ «Greatest Common Factor». www.mathsisfun.com. Retrieved 2020-08-30.
- ^ Slavin, Keith R. (2008). «Q-Binomials and the Greatest Common Divisor». INTEGERS: The Electronic Journal of Combinatorial Number Theory. University of West Georgia, Charles University in Prague. 8: A5. Retrieved 2008-05-26.
- ^ Schramm, Wolfgang (2008). «The Fourier transform of functions of the greatest common divisor». INTEGERS: The Electronic Journal of Combinatorial Number Theory. University of West Georgia, Charles University in Prague. 8: A50. Retrieved 2008-11-25.
- ^ Knuth, Donald E. (1997). The Art of Computer Programming. Vol. 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley Professional. ISBN 0-201-89684-2.
- ^ Shallcross, D.; Pan, V.; Lin-Kriz, Y. (1993). «The NC equivalence of planar integer linear programming and Euclidean GCD» (PDF). 34th IEEE Symp. Foundations of Computer Science. pp. 557–564. Archived (PDF) from the original on 2006-09-05.
- ^ Chor, B.; Goldreich, O. (1990). «An improved parallel algorithm for integer GCD». Algorithmica. 5 (1–4): 1–10. doi:10.1007/BF01840374. S2CID 17699330.
- ^ Adleman, L. M.; Kompella, K. (1988). «Using smoothness to achieve parallelism». 20th Annual ACM Symposium on Theory of Computing. New York. pp. 528–538. doi:10.1145/62212.62264. ISBN 0-89791-264-0. S2CID 9118047.
- ^ Müller-Hoissen, Folkert; Walther, Hans-Otto (2012), «Dov Tamari (formerly Bernhard Teitler)», in Müller-Hoissen, Folkert; Pallo, Jean Marcel; Stasheff, Jim (eds.), Associahedra, Tamari Lattices and Related Structures: Tamari Memorial Festschrift, Progress in Mathematics, vol. 299, Birkhäuser, pp. 1–40, ISBN 978-3-0348-0405-9. Footnote 27, p. 9: «For example, the natural numbers with gcd (greatest common divisor) as meet and lcm (least common multiple) as join operation determine a (complete distributive) lattice.» Including these definitions for 0 is necessary for this result: if one instead omits 0 from the set of natural numbers, the resulting lattice is not complete.
- ^ Knuth, Donald E.; Graham, R. L.; Patashnik, O. (March 1994). Concrete Mathematics: A Foundation for Computer Science. Addison-Wesley. ISBN 0-201-55802-5.
- ^ Nymann, J. E. (1972). «On the probability that k positive integers are relatively prime». Journal of Number Theory. 4 (5): 469–473. Bibcode:1972JNT…..4..469N. doi:10.1016/0022-314X(72)90038-8.
- ^ Chidambaraswamy, J.; Sitarmachandrarao, R. (1987). «On the probability that the values of m polynomials have a given g.c.d.» Journal of Number Theory. 26 (3): 237–245. doi:10.1016/0022-314X(87)90081-3.
References[edit]
- Andrews, George E. (1994) [1971], Number Theory, Dover, ISBN 978-0-486-68252-5
- Hardy, G. H.; Wright, E. M. (1979), An Introduction to the Theory of Numbers (Fifth ed.), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 71081766
Further reading[edit]
- Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Section 4.5.2: The Greatest Common Divisor, pp. 333–356.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 31.2: Greatest common divisor, pp. 856–862.
- Saunders Mac Lane and Garrett Birkhoff. A Survey of Modern Algebra, Fourth Edition. MacMillan Publishing Co., 1977. ISBN 0-02-310070-2. 1–7: «The Euclidean Algorithm.»
Что такое «НОД», как расшифровывается аббревиатура «НОД», теория, примеры и найдем «НОД» на калькуляторе.
Что такое «НОД»
Аббревиатура «НОД» расшифровывается как : «Наибольший общий делитель«.
Что такое Наибольший общий делитель
Наибольшим общим делителем (НОД) для двух целых чисел, называется число, которое может делить эти два числа без остатка — таких чисел может быть несколько, но самое большое из них и будет «Наибольший общий делитель«.
Далее рассмотрим пример, который мы использовали ниже, найдем вся числа, на которые делятся эти два числа:
12 и 18
Это будет… пойдем по возрастающей , первое число это —
2
:
12 : 2 = 9, 18 : 2 = 9
Второе число —
3
:
12 : 3 = 4, 18 : 3 = 6
Третье число —
6
:
12 : 6 = 2, 18 : 6 = 3
Далее общих делителей нет, поэтому выбираем больший из всех делителей — 2, 3, 6 — из этих трех цифр, самое большое — 6. Значит
Наибольший общий делитель для двух чисел 12 и 18 будет 6.
Способы нахождения «НОД»
«НОД» можно находить несколькими способами :
Метод разложения на множители, на начальном этапе тоже самое, что и НОК, только выборка числа/чисел — наоборот.
Алгоритм Евклида для нахождения НОД.
Или на калькуляторе, который умеет это делать.
Какой из этих методов вам использовать для нахождения «НОД» — это ваш выбор.
Пример нахождения «НОД» методом разложения на множители
Для того чтобы найти «НОД» двух чисел нам понадобится пример.
Давайте предположим, что у нас есть два числа :
12 и 18
Раскладываем на множители оба числа и получим :
Строчка №1. Разложенное на множители число 12 :
12 = 2 * 2 * 3
Строчка №2. И разложенное число 18 :
18 = 2 * 3 * 3
Вычленяем одинаковые числа из первой и второй строчек :
12 = 2 * 2 * 3
…
18 = 2 * 3 * 3
Как видим, что у нас повторяются две цифры 2 * 3. Перемножаем 2 * 3 = 6
Результат нахождения «НОД»-а двух чисел
«НОД» двух чисел 12 и 18 равен 6.
Проверить правильность вычисления нода чисел можно на калькуляторе.
Алгоритм Евклида для нахождения НОД
Рассмотрим, также, алгоритм Евклида для нахождения НОД Возьмем пример из выше идущего примера :
12 и 18
: Записываем большее число(18) слева далее равно.
После равно записываем вторе число — 12.
Делим большее число на меньшее 18 : 12 = 1.5. Делится с остатком, поэтому берем целое 1 и умножаем на делитель 12 , 1 * 12 = 12. Отнимаем от 18, 18 -12 = 6. Получили остаток 6.
Записанная первая строчка должна выглядеть так:
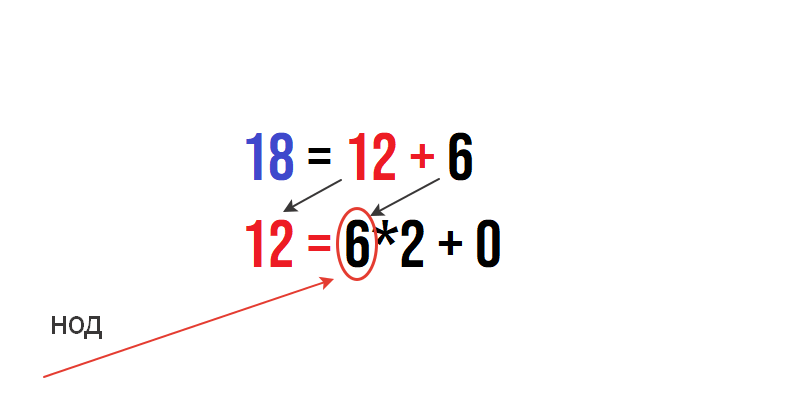
18 = 12 + 6
Строчка №2
: Далее 12 сносим на вторую строчку, далее равно и за равно ставим остаток 6.
Делим 12 на 6, 12 : 6 = 2. Делится без остатка, поэтому будем прибавлять ноль.
Вторая строчка у нас получится таким образом : 12 = 6*2 + 0.
12 = 6*2 + 0
Как только дальнейшие действия невозможны, то первое число после равно(справа) — это и будет наш «НОД» = 6.
Как найти НОД на нашем калькуляторе!?
Для того, чтобы найти «НОД» вам потребуется наш калькулятор
Пример нахождения НОД на калькуляторе
К примеру нам требуется найти наибольший общий делитель для чисел 12 и 18.
Набираем число 12, как обычно на калькуляторе.
Выбираем кнопку – нод.
Стандарно набираем второе число 18.
Стандарно нажимаем равно… результат:
Загрузить PDF
Загрузить PDF
Нахождение наибольшего общего делителя (НОД) для определенного количества чисел может быть легкой задачей, если вы умеете это делать.
-
1
Найдите делители чисел. Начните с поиска всех делителей первого и второго числа.
-
2
Сравните делители обоих чисел и найдите самое большое число, которое есть в списке делителей как первого, так и второго числа. Это число равно НОД.
Реклама
-
1
Разложите каждое число на простые множители. Простое число — это число, большее 1 и которое делится только на 1 и на само себя. Примеры простых чисел: 5, 17, 97, 331.
-
2
Найдите общие простые множители. Общий простой множитель может быть только один, или их может быть несколько.
-
3
Если у двух чисел есть только один общий простой множитель, то он равен НОД. Если у двух чисел есть несколько общих простых множителей, то их произведение равно НОД.
-
4
Изучите пример. Чтобы продемонстрировать этот метод, изучите пример, приведенный на рисунке.
Реклама
Советы
- Простое число — это число, которое делится только на 1 и на само себя.
- Знаете ли вы, что в третьем веке до н.э. математик Евклид создал алгоритм для вычисления наибольшего общего делителя двух натуральных чисел и двух многочленов?
Реклама
Об этой статье
Эту страницу просматривали 7409 раз.
























![R=mathbb {Z} left[{sqrt {-3}},,right],quad a=4=2cdot 2=left(1+{sqrt {-3}},,right)left(1-{sqrt {-3}},,right),quad b=left(1+{sqrt {-3}},,right)cdot 2.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a3f756caa5d39d36a00f069a49cde49153d1c9f)








