Алгоритм Евклида — нахождение наибольшего общего делителя
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Решение задачи на языке программирования Python
Алгоритм нахождения НОД делением
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
a = int(input()) b = int(input()) while a != 0 and b != 0: if a > b: a = a % b else: b = b % a print(a + b)
В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для определения НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.
Если условием завершения цикла является равенство хотя бы одной из переменных нулю (a == 0 or b == 0), то условием продолжения его работы является обратное этому условие — обе переменные должны иметь отличные от нуля значения (a != 0 and b != 0).
Для того, чтобы вышеприведенная программа могла обрабатывать отрицательные числа, в логическом выражении при if должны сравниваться модули значений переменных: if abs(a) > abs(b):. Иначе большим числом может оказаться меньшее по модулю. В этом случае интерпретатор Питона в качестве остатка от деления выдает вещественное число. В результате это приводит к зацикливанию, так как низвести переменные до нуля становится как минимум маловероятным.
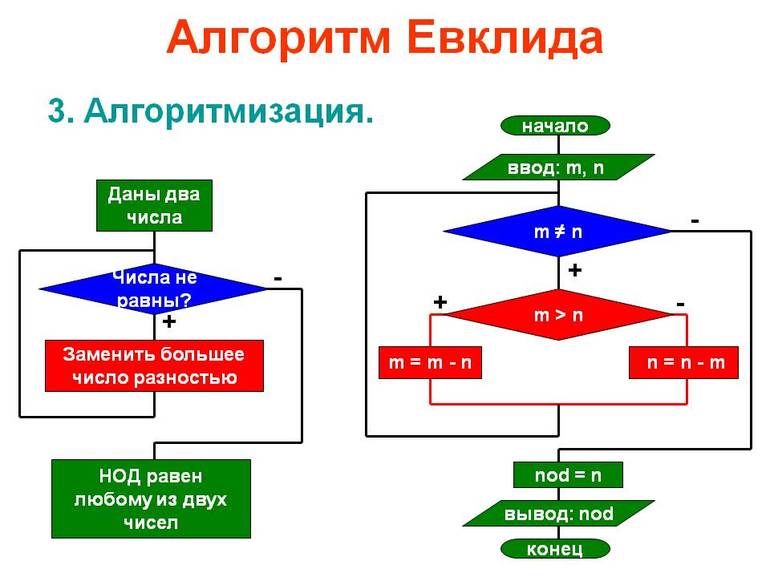
Алгоритм нахождения НОД вычитанием
- Из большего числа вычитаем меньшее.
- Если получается 0, значит, числа равны друг другу и являются НОД (следует выйти из цикла).
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6
a = int(input()) b = int(input()) while a != b: if a > b: a = a - b else: b = b - a print(a)
Функция, вычисляющая НОД
def gcd(m, n): while m != n: if m > n: m = m - n else: n = n - m return n a = int(input()) b = int(input()) print(gcd(a, b))
Функция gcd модуля math
В модуле math языка программирования Python есть функция gcd, вычисляющая наибольший общий делитель двух чисел.
>>> import math >>> math.gcd(30, 18) 6
Больше задач в PDF
Как найти НОД двух чисел по алгоритму Евклида
Содержание:
- Что такое алгоритм Евклида
- Понятие НОД
-
Основная суть алгоритма Евклида
- Последовательность нахождения НОД при помощи деления:
- Последовательность нахождения НОД при помощи вычитания:
- Примеры решения задач с алгоритмом Евклида
Что такое алгоритм Евклида
Алгоритм Евклида — один из наиболее ранних численных алгоритмов в истории. Название было дано в честь греческого математика Евклида, который впервые дал ему описание в книгах «Начала». Изначально назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль. Сегодня чаще используется взятие остатка от деления вместо вычитания, но суть метода сохранилась.
Алгоритм Евклида — это алгоритм, основная функция которого заключается в поиске наибольшего общего делителя (НОД) для двух целых чисел.
Простейшим случаем применения данного алгоритма является поиск наибольшего общего делителя для пары положительных целых чисел. Евклид, автор этого метода, предполагал его использование только для натуральных чисел и геометрических величин. Но позже алгоритм был обобщен и для других групп математических объектов, что привело к появлению такого понятия, как евклидово кольцо.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Понятие НОД
Аббревиатура НОД расшифровывается как «наибольший общий делитель».
Наибольший общий делитель — делитель, который делит без остатка два числа, при этом сам делится без остатка на любой другой делитель исходных двух чисел. То есть это самое большое число, на которое без остатка можно разделить пару чисел, для которых подбирается НОД.
Основная суть алгоритма Евклида
Суть алгоритма заключается в построении ряда следующего вида (при условии, что a больше b):
a, b, x1, x2, x3, … xn.
В нем каждое последующее число — это остаток от деления двух предыдущих, ряд заканчивается, когда остаток от деления становится равным 0 — при условии использования деления.
В нем каждое последующее число является результатом вычитания двух предыдущих, ряд заканчивается, когда частное становится равным 0 — при условии использования вычитания.
Последовательность нахождения НОД при помощи деления:
- Большее число делится на меньшее.
- Если результат деления:
- без остатка, то меньшее число и есть НОД;
- с остатком, тогда большее число заменяется на остаток.
- Переход к пункту 1.
Пример №1
60 / 36 = 1 (остаток 24)
36 / 24 = 1 (остаток 12)
24 / 12 = 2 (остаток 0)
НОД для 60 и 36 равен 12 (делитель).
Последовательность нахождения НОД при помощи вычитания:
- Из большего числа вычитается меньшее.
- Если результат вычитания:
- равен 0, то числа равны друг другу и являются НОД;
- не равен 0, в таком случае большее число заменяется на результат вычитания.
- Переход к пункту 1.
Пример №2
60 — 36 = 24
36 — 24 = 12
24 — 12 = 12
12 — 12 = 0
НОД для 60 и 36 равен 12 (уменьшаемое, вычитаемое)
Примеры решения задач с алгоритмом Евклида
Задача №1
Найти наибольший общий делитель для чисел 128 и 96.
Решение:
128 — 96 = 32
96 — 32 = 64
64 — 32 = 32
32 — 32 = 0
Или
128 / 96 = 1 (остаток 32)
96 / 32 = 3
Ответ: 32
Задача №2
Найти наибольший общий делитель для чисел 37 и 17.
Решение:
37 / 17 = 2 (остаток 3)
17 / 3 = 5 (остаток 2)
3 / 2 = 1 (остаток 1)
2 / 1 = 2 (остаток 0)
Или
37 — 17= 20
20 — 17 = 3
17 — 3 = 14
14 — 3 = 11
11 — 3 = 8
8 — 3 = 5
5 — 3 = 2
3 — 2 = 1
2 — 1 = 1
1 — 1 = 0
Числа 37 и 17 являются простыми, соответственно, их НОД — единица. Совет: перед вычислениями проверяйте таблицу простых чисел.
Ответ: 1
Насколько полезной была для вас статья?
Рейтинг: 4.50 (Голосов: 18)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Время на прочтение
8 мин
Количество просмотров 19K
Алгоритмы – одна из центральных тем в программировании, они повсюду (особенно на собеседованиях, ха-ха).
(Разве можно обойтись в таком посте без «баяна»?)
Одним из самых известных является так называемый алгоритм Евклида – пожалуй, самый распространенный способ нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел. С него также зачастую любят начинать изучение (и обучение) соответствующих разделов математики и информатики.
А Дональд Кнут, небезызвестный автор трактата “Искусство программирования” (и не только), и вовсе считает алгоритм первым в истории (по крайней мере, относительно современных определений). Потому что, не смотря на то, что алгоритм был придуман и использовался еще до, собственно, Евклида, который жил в IV-III вв. до нашей эры (он упоминается уже у Аристотеля, жившего веком ранее), Евклид описывает процесс итеративно, что согласуется с современным значением слова.
Само слово “алгоритм” восходит к имени персидского математика Аль-Хорезми, жившего примерно в VIII-IX вв. уже нашей эры. А началом его использования в смысле, близком современному, считается уже лишь XX век, точнее – его первые десятилетия, восход информационных технологий.
Алгоритм Евклида
Любопытства ради предлагаю ознакомиться с евклидовским описанием алгоритма в редактуре Кнута. Оно довольно длинное, поэтому спрятано под катом:
Описание алгоритма Евклида, близкое к исходному
Предложение. Для данных двух положительных целых чисел найти их наибольший общий делитель.
Пусть A и C – два заданных положительных целых числа; требуется найти их НОД. Если число A делится на C, то число C есть общий делитель чисел C и A, поскольку оно делит самое себя. И очевидно, что оно будет и наибольшим делителем, поскольку нет числа большего, чем число C, которое бы делило C.
Но если C не делит число A, то будем непрерывно вычитать меньшее из чисел A и C из большего до тех пор, пока не получим число, которое нацело делит предыдущее вычитаемое. Это должно рано или поздно произойти, потому что, если разность будет равна единице, то единица будет делить предыдущее вычитаемое.
Теперь положим, что E – положительный остаток от деления числа A на C; пусть F – положительный остаток от деления числа C на число E и пусть F делит E. Так как F делит E, а E делит C — F, F также делит C — F. Но оно делит и самое себя, поэтому F делит C, а C делит A — E; поэтому F делит также A — E, но оно делит и E; поэтому F делит A. Следовательно F является общим делителем чисел A и C.
Теперь я утверждаю, что оно является и НОД. Действительно, если F – не наибольший общий делитель чисел A и C, то найдется большее число, которое будет делить оба этих числа. Пусть таким числом будет G.
Так как число G делит число C, а число C – делит A — E, то G также делит число A — E. Число G делит также все число A, поэтому оно делит и остаток E. Но E делит C — F, поэтому G также делит C — F. А число G также делит все число C, так как оно делит и остаток F; таким образом, большее число делит меньшее, а это невозможно.
Таким образом, нет такого числа, большего, чем F, которое бы делило A и C; значит, число F является НОД.
Следствие. Это рассуждение делает очевидным предположение, что всякое число, делящее два числа, делит и их НОД. Ч.т.д.
Описание приводит два способа нахождения НОД – вычитанием и делением. Собственно, и в наши дни широко известны эти два способа реализации алгоритма.
Вот пример функции, написанной на «Swift», реализации первого способа:
func subtractionGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
while firstNumber != 0, secondNumber != 0 {
if firstNumber > secondNumber {
firstNumber = firstNumber - secondNumber
} else {
secondNumber = secondNumber - firstNumber
}
}
return firstNumber + secondNumber // One of them is 0.
}Здесь, переиспользования ради, я вынес в отдельную функцию случаи поиска НОД, когда он известен сразу, без необходимости следования какому-либо алгоритму:
func simpleCasesGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int? {
if firstNumber == secondNumber {
return firstNumber // Any.
}
if firstNumber == 0 {
return secondNumber
}
if secondNumber == 0 {
return firstNumber
}
return nil
}(Если два числа равны, то, естественно, их НОД также равен им. Если какое-то из чисел равно нулю, то НОД будет равняться второму числу, т.к. ноль делится любым числом (с результатом, понятное дело, тоже ноль).)
В качестве входных данных могут использоваться только неотрицательные значения. Соответственно, для отрицательных можно использовать те же методы, но взяв числа по модулю. (Да, общий делитель может быть и отрицательным, но мы ищем именно НОД, а положительные числа, очевидно, всегда больше отрицательных.)
А вот так может выглядеть реализация версии алгоритма делением:
func divisionGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
while firstNumber != 0, secondNumber != 0 {
if firstNumber > secondNumber {
firstNumber = firstNumber % secondNumber
} else {
secondNumber = secondNumber % firstNumber
}
}
return firstNumber + secondNumber // One of them is 0.
}Вторая версия в наши дни считается предпочтительней, так как содержит в себе, в среднем, ощутимо меньшее количество шагов. Тем не менее, во времена, когда компьютеры были большие и медленные, операция деления могла быть сама по себе сложной процедурой. И тогда первая версия алгоритма могла оказаться эффективней.
Чтобы немного их сравнить, я произвел несколько замеров с использованием любимого мной метода measure(_:) класса XCTestCase «нативного» фреймворка для тестирования кода в Xcode-проектах XCTest.
В качестве входных данных я использовал массив пар случайных чисел. Замеры производились, естественно, с использованием одного и того же массива для каждого способа. Разброс чисел для пар я взял от нуля до 9999. Замеры производились на количестве вычислений (пар чисел): одно, десять, 100, 1000, 10000, 100000, 1000000 и 10000000. Последнее заставляло ожидать результата уже несколько минут, поэтому на нем я решил остановиться.
Вот простой код генерации входных данных:
let pairs = (0..<100).map { _ in (Int.random(in: 0..<10000), Int.random(in: 0..<10000)) } // Generates 100 pairs.Сам замер выглядит, например, так:
func testSubstractionGCDPerformance() {
measure() {
_ = pairs.map { substractionGCD($0, $1) }
}
}А вот так выглядят результаты запуска на моем компьютере:
(Subtraction – вычитание, division – деление.)
В общем, очень хорошо видно, как сильно на современных компьютерах проигрывает метод вычитания.
«Улучшенная» версия алгоритма Евклида
В литературе можно встретить версию алгоритма, в которой одно из чисел на каждом шаге вместо остатка от деления на второе заменяется на разность между этим отстатком и вторым числом, но только в случае, если остаток от деления больше половины второго числа. Реализация этой версии может выглядеть так:
func improvedDivisionGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
while firstNumber != 0, secondNumber != 0 {
if firstNumber > secondNumber {
let firstNumberClaim = firstNumber % secondNumber
if firstNumberClaim > secondNumber / 2 {
firstNumber = abs(firstNumberClaim - secondNumber)
} else {
firstNumber = firstNumberClaim
}
} else {
let secondNumberClaim = secondNumber % firstNumber
if secondNumberClaim > firstNumber / 2 {
secondNumber = abs(secondNumberClaim - firstNumber)
} else {
secondNumber = secondNumberClaim
}
}
}
return firstNumber + secondNumber // One of them is 0.
}Такая модификация сокращает количество шагов алгоритма, но, судя по результатам замеров на моем компьютере, дополнительные вычисления и проверки на каждом шаге, нейтрализуют это преимущество и даже более:
(Improved – «улучшенная» версия.)
Еще немного о значимости алгоритма Евклида
Алгоритм имеет также геометрическую версию (для нахождения наибольшей меры двух отрезков).
Алгоритм был, конечно, обощен и для нахождения НОД любого количества чисел, не только двух. В двух словах идея такова: если обозначить функцию поиска НОД двух чисел как gcd(a, b), то, скажем, НОД трех чисел gcd(a, b, c) равен gcd(gcd(a, b), c). И так далее, для любого количества чисел НОД находится последовательным вычислением НОД НОД-а предыдущей пары чисел и следующего числа. Хотя, конечно, это касается поиска НОД вообще, а не только алгоритма Евклида.
Существует также обощение алгоритма для нахождения НОД полиномов. Но это уже выходит за рамки этого несложного поста, а в некоторой степени, и моих познаний в математике.
Сложность алгоритма Евклида
Временная сложность алгоритма исследовалась давно, не быстро и гораздо более учеными мужами, чем ваш покорный слуга. Тем не менее, вопрос давно закрыт и ответ получен. Собственно, еще в середине позапрошлого века. Габриэлем Ламе.
Если коротко, то ответ формулируется, собственно, теоремой Ламе, связанной с этим алгоритмом. Количество шагов алгоритма будет равно порядковому номеру ближайшего большего числа Фибоначчи наименьшему из двух чисел входных параметров минус 2. Оперируя чуть более традиционно-математическими обозначениями, то если u > v (и v > 1), то число проходов алгоритма будет равняться n — 2 при v < Fn (Fn – это некое ближайшее v число Фибоначчи, а n – это его порядковый номер).
Числа Фибоначчи растут экспоненциально, соответственно, имеем логарифмическую функцию времени выполнения алгоритма (от меньшего из двух входных чисел).
Те же самые выкладки показывают, что наихужшие для алгоритма входные данные – это два последовательных числа Фибоначчи.
Бинарный метод поиска НОД
Говоря о поиске НОД, стоит быть упомянутым алгоритм, предложенный уже в 60-е годы прошлого столетия неким Джозефом Стейном, о котором я не нашел в Сети вообще никакой информации. Он (алгоритм) ориентирован на двоичную арифметику и не содержит операций деления. Алгоритм оперирует только проверками четности и делением пополам, что осуществимо возможностями одной лишь бинарной арифметики.
Алгоритм основывается на четырех фактах:
- Если u и v оба четны, то gcd(u, v) = 2 * gcd(u / 2, v / 2);
- Если u четно, а v – нет, gcd(u, v) = gcd(u / 2, v);
- gcd(u, v) = gcd(u — v, v) (это следует из алгоритма Евклида);
- Если u и v оба нечетны, то u — v – четно и |u — v| < max(u, v)
На «Wikipedia» можно посмотреть рекурсивную версию алгоритма (на современных языках программирования записывается в несколько строк), я не стал ее переписывать на «Swift». А здесь я приведу вариант итеративной реализации:
func binaryGCD(_ firstNumber: Int, _ secondNumber: Int) -> Int {
if let simpleGCD = simpleCasesGCD(firstNumber, secondNumber) {
return simpleGCD
}
var firstNumber = firstNumber
var secondNumber = secondNumber
var shift = 0
while (firstNumber | secondNumber) & 1 == 0 {
shift += 1
firstNumber >>= 1
secondNumber >>= 1
}
while firstNumber & 1 == 0 {
firstNumber >>= 1
}
repeat {
while secondNumber & 1 == 0 {
secondNumber >>= 1
}
if firstNumber > secondNumber {
swap(&firstNumber, &secondNumber)
}
secondNumber -= firstNumber
} while secondNumber != 0
return firstNumber << shift
}Сделав замеры на тех же данных, к сожалению, этот мудреный алгоритм на моем компьютере не оправдал возложенных на него надежд. Конечно, он все еще работает в два раза быстрее евклидова алогоритма вычитанием, но заметно уступает классической его версии с делением. Полная таблица сводных данных:
(Binary – бинарный алгоритм.)
(Не исключаю, что алгоритм можно записать более эффективно, чем это сделал я, и это повлияет на результат, но на что же нам тогда нужны компиляторы?!)
Кстати, этот алгоритм, безусловно, получивший свои 15 минут славы уже в век информационных технологий (в более раннюю его часть, чем текущая), был известен еще в Древнем Китае. Его описание обнаружено в трудах, датируемых I в. н.э. Конечно, в терминах вроде «половинного деления» и вычитания. А также в контексте сокращения дробей.
Заключение
Честно говоря, этим простеньким «исследованием» я не собирался ничего доказывать и не хотел делать какие-то революционные умозаключения (и ведь не сделал же!). Я всего лишь хотел удовлетворить свое любопытство, посмотреть на работу разных подходов для решения классической задачи и слегка размять пальцы. Тем не менее, я надеюсь, наблюдать результаты было любопытно и вам!
Алгоритм нахождения НОД и НОК
Скачать материал

Скачать материал


- Сейчас обучается 27 человек из 13 регионов


- Сейчас обучается 136 человек из 42 регионов


- Сейчас обучается 75 человек из 34 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Алгоритм нахождения НОД и НОК
-
2 слайд
Наибольший общий делитель (НОД)
Наибольший общий делитель (НОД) двух данных чисел «a» и «b» — это наибольшее число, на которое оба числа «a» и «b» делятся без остатка. -
3 слайд
Нахождение НОД
Чтобы найти НОД двух или более натуральных чисел нужно:
1) Разложить числа на простые множители.
2) Взять одинаковые простые множители в обоих числах.
3) Найти произведение одинаковых простых множителей. -
4 слайд
Найдем НОД двух чисел 30 и 18
30=2*3*5
18=2*3*3
НОД=2*3=6 -
5 слайд
Определите НОД 2450 и 3500
-
6 слайд
Определите НОД 324, 111 и 432
-
7 слайд
Что такое алгоритм?
Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения некоторого результата -
8 слайд
Пример алгоритма из жизни
-
9 слайд
Евклид
Евкли́д или Эвкли́д (др.-греч. Εὐκλείδης, от «добрая слава», время расцвета — около 300 года до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III в. до н. э.
Евклид — первый математик Александрийской школы. Его главная работа «Начала» (Στοιχεῖα, в латинизированной форме — «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию древнегреческой математики и создал фундамент дальнейшего развития математики. Из других его сочинений по математике надо отметить «О делении фигур», сохранившееся в арабском переводе, 4 книги «Конические сечения», материал которых вошёл в произведение того же названия Аполлония Пергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Паппа Александрийского. Евклид — автор работ по астрономии, оптике, музыке и др. -
10 слайд
Алгоритм Евклида
Алгоритм Евклида – это алгоритма нахождения НОД.
Выделяют два способа реализации алгоритма: методом деления и методом вычитания. Рассмотрим отдельно каждый из них. -
11 слайд
Метод вычитания
Из большего числа вычитаем меньшее.
Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
Переходим к пункту 1. -
12 слайд
Блок-схема алгоритма Евклида (Вычитанием)
-
13 слайд
Метод деления
Большее число делим на меньшее.
Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
Если есть остаток, то большее число заменяем на остаток от деления.
Переходим к пункту 1. -
14 слайд
Блок-схема алгоритма Евклида (делением)
-
15 слайд
Реализация алгоритма в программе Кумир (вычитание)
-
16 слайд
Реализация алгоритма в программе Кумир (деление)
-
17 слайд
Реализация алгоритма Евклида на языке программирования Python
-
18 слайд
Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка. -
19 слайд
Алгоритм нахождения НОК
Для нахождения НОК при помощи алгоритма Евклида нужно:
1. Найти НОД по описанным выше алгоритмам.
2. Разделить произведение чисел m и n на НОД -
20 слайд
Найдем НОК чисел 30 и 18
НОД(30,18)=6
НОК=30*12:6=60 -
-
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 264 743 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Скачать материал
-
10.11.2017
19556
-
PPTX
839.8 кбайт -
84
скачивания -
Рейтинг:
2 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Минеев Дмитрий Юрьевич. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 21249
-
Всего материалов:
4
Общие сведения
Математики называют алгоритм Евклида для нахождения НОД взаимным вычитанием. Древнегреческий ученый впервые применил его для двух целых чисел. Позднее это новшество использовалось для нахождения наибольшей величины делителя двух однородных величин (отрезков, земельных участков и т. д. ). Он является старым и эффективным численным алгоритмом. Его применение следует объяснять для пары положительных целых чисел, хотя можно использовать правило и для десятичных дробей. Его изучают в старших классах.
Суть алгоритма заключается в формировании новой пары чисел из меньшего и разницы между большим и меньшим элементом. Процесс, состоящий из арифметических операций, повторяется до тех пор, пока числа не будут равны друг другу. Первоначально инструкция создавалась для натуральных чисел и геометрических величин. Однако в XIX веке ее расширили и стали применять для других объектов: целых чисел Гаусса и многочленов с одной переменной (полиномов). Направление, получившееся в математике, специалисты стали называть евклидовым кольцом. Позднее его доработали и стали применять для узлов и многомерных полиномов.
Алгоритм является основой для криптографического шифрования с открытым ключом, который распространен в электронной коммерции для защиты программных продуктов от злоумышленников. Его применяют для решения уравнений Диофанта, построения дробей непрерывного типа, доказательств утверждений (основная теорема арифметики и теорема Лагранжа о сумме 4 квадратов).
Описание и доказательство алгоритма
Для целых чисел алгоритм состоит из соотношений, количество которых равно числу элементов. Если предположить, что а и b являются целыми и неравными нулю значениями, то для них выполняется соотношение a > b > R1 > … > Rn. Величинами R с определенными индексами являются остатки от деления а на некоторое значение Q1 и b на Q2. Описывается процесс такими формулами:
- а = b * q0 + R1.
- b = R1 * q1 + R2.
- R1 = R2 * Q2 + R3.
- Rn-1 = Rn * Qn.
На последнем этапе не должно быть остатка. Для отрезков применяется геометрический алгоритм. Чтобы найти наибольший общий отрезок, нужно из большего вычесть меньший, а затем заменить первый их разностью. Операцию следует завершить при равенстве двух отрезков. Реализуется данный алгоритм при помощи циркуля и линейки. Для доказательства алгоритма Евклида следует взять пару чисел f и g, для которых можно привести такие утверждения:
- Делители f и g — общие делители (f — g) и g.
- Делители (f — g) и g — общие делители f и g.
- Когда f > g, тогда НОД (f, g) = НОД (f — g, g).
- НОД (f, 0) = f.
Для доказательства следует ввести новую переменную z. Она является общим делителем для f и g. Кроме того, разность f — g также делится на z. Из предположения f = z * k и g = z * s следует, что f — g = z * k — z * s = z * (k — s). Иными словами, z — общий множитель для f — g. Из соотношения можно доказать, что z делит не только разность, но и сумму: f — g + g = f. Следовательно, z — общий делитель для f и g.
На основании полученных вычислений можно сделать вывод, что z для f и g совпадает с (f — g) и g. Если одно из чисел имеет нулевое значение, то НОД равен другому числу, поскольку 0 делится на любое число.
Следует отметить, что методика для нескольких чисел (трех и более) аналогичная. В этом случае нужно брать не одну разность, а две, в которой будет присутствовать минимальное число. Данный алгоритм применяется в построении программного обеспечения. Однако перед написанием кода следует сначала составить блок-схему. Она позволит избежать ошибок, а также внимательно сосредоточиться на проекте.
Применение в математике
Одним из примеров алгоритма Евклида считается соотношение Безу (лема или тождество). Его суть заключается в представлении НОД в форме линейной комбинации с некоторыми коэффициентами целого типа. Лема имеет следующую формулировку: для целых чисел f и g (хотя бы одно из них не равно 0) существуют некоторые коэффициенты целого типа, для которых справедливо соотношение НОД (f, g) = m * f + n * g, где m и n — коэффициенты Безу.
Тождество справедливо и для натуральных чисел. У него такая же формулировка, только слово «целых» заменяется на «натуральных». Кроме того, существует расширенный алгоритм Евклида:
- R1 = f + g * (-Q0).
- R2 = g — R1 * Q1 = f * (-Q1) + g * (1 + Q1 * Q0).
- Для целых w и z: НОД (f, g) = Rn = f * w + g * z.
Еще одним примером использования алгоритма считаются цепные дроби. Пусть f и g — числитель и знаменатель соответственно. Любая дробь такого типа может быть представлена следующим образом: f / g = [Q0;Q1,Q2,…, Qn]. Без Qn она равна отношению коэффициентов Безу w / z, результат которого нужно брать с отрицательным знаком, т. е. [Q0;Q1,Q2,…, Qn-1] = — w / z. Следовательно, равенства могут иметь такое представление:
- f / g = Q0 + R0 / b.
- b / R0 = Q1 + R1 / R0.
- R0 / R1 = Q2 + R2 / R1.
- (Rn-2) / (Rn-1) = Qn.
Если обратить внимание, то можно понять закономерность: последний элемент правой части равен обратной величине левой части последующего тождества. В результате этого можно объединить две формулы: f / g = Q0 + 1 / [Q1 + (R1/R0)]. Третья применяется для замены знаменателя: f / g = Q0 + 1 / [Q1 + (1 / (Q2 + (R2/R1)))]. Следовательно, можно записать цепную дробь в таком виде: f / g = Q0 + 1 / [Q1 + (1 / (Q2 + … + 1 / Qn))].
Алгоритм применяется и для решения диофантовых уравнений. Диофантовым является уравнение с целыми коэффициентами и одной или несколькими переменными, решение которого сводится к нахождению только целых корней. Решений у него может быть много. Примером простейшего считается обыкновенное линейное с двумя переменными Ах + Ву = С, где А и В — некоторые коэффициенты. Переменными величинами являются х и у. Решается оно следующим образом:
- Находится коэффициент D: D = НОД (А, В).
- При помощи расширенного алгоритма Евклида следует найти некоторые коэффициенты w, z: А * w + B * z = D.
- Получаются такие соотношения (x = w, y = z) при D = С: С = Q * D, х = Q * w и y = Q * z.
- Частное решение: Ах + Ву = А * (Q * w) + B * (Q * z) = Q * (A * w + B * z) = Q * D = C.
Если у уравнения всего один корень, то C кратно D. Данное утверждение следует из соотношения, в котором D делит А, В и всю левую сторону, а значит, должно делить правую на С.
Различные вариации
Кольцо является алгебраическим выражением или структурой, в которой применяются операции сложения (обратимого) и умножения эквивалентные соответствующим действиям над некоторыми числами. Примером считается обобщенные множества целых, дробных и комплексных чисел. Более сложный пример — различные функции с элементами кольца. Если к данному множеству применима лема Евклида, то его называют Евклидовым кольцом. К ним относятся кольца целых чисел и многочленов.
Для многочлена вида Z[g] от одной неизвестной g над некоторым полем (функцией) Z определена операция деления. Последняя выполняется только с остатком. Если применить к нему правило Евклида, то получится последовательность остатков в виде полиномов. Для примера следует разобрать такую задачу: пусть cont (w) является НОД для коэффициентов f (w) из полинома Z[g]. При делении f (w) на cont (w) образуется примитивная часть многочлена primpart (f (w)). Необходимо найти НОД Р1 (g) и Р2 (g). Если числа являются целыми, то в этом случае верны такие тождества:
- сont (НОД {Р1 (g), Р2 (g)}) = НОД{сont (Р1 (g)), сont (Р2 (g))}.
- primpart (НОД {Р1 (g), Р2 (g)}) = НОД{primpart (Р1 (g)), primpart (Р2 (g))}.
Следовательно, поиск НОД для двух многочленов нужно свести к поиску НОД примитивных полиномов. Для примитивных полиномов Р1 (g) и Р2 (g), принадлежащих Z[g], выполняется такое соотношение между их степенями: deg (Р1 (g)) = m и deg (Р2 (g)) = n (m > n). Деление с остатком осуществляется по псевдоделимости, поскольку иногда выполнить первую процедуру невозможно.
В результате этого вводят специальный алгоритм для псевдоделения, результатом которого является псевдоостаток. Его обозначают «prem». Формула операции псевдоделения имеет такой вид с учетом псевдочастного Q (g) и псевдоостатка R (g): [lc (P2 (g))^(m-n+1)] * P1 (g) = P2 (g) * Q (g) + R2 (g) при deg (R (g)) < deg (P2 (g)). Следовательно, P1 (g) и P2 (g) принадлежат Z[g] при условии, что deg (P1) = n1 >= deg (P2) = n2. На основании полученных результатов лема Евклида состоит из таких пунктов:
- Найти НОД: НОД{сont (Р1 (g)), сont (Р2 (g))}.
- Расчет примитивных частей: [P1 (g)]’ = primpart (P1 (g)) и [P2 (g)]’ = primpart (P2 (g)).
- Последовательность псевдоостатков полиномного типа: [P1 (g)]’, [P2 (g)]’, [P3 (g)]’ = prem ([P1 (g)]’, [P2 (g)]’), [P4 (g)]’ = prem ([P2 (g)]’, [P3 (g)]’),…, [Pn (g)]’ = prem ([(Pn-2)(g)]’, [(Pn-1)(g)]’).
- Возвратить результат: если deg (Pn (g)) = 0, то вернуть НОД{сont (Р1 (g)), сont (Р2 (g))}. Иначе — выражение в первом пункте нужно умножить на primpart (Pn (g)).
Существует еще одна разновидность алгоритма. Она называется ускоренной. Ее суть заключается в применении понятия симметричного остатка: Ri = Ri-2 * (mod [Ri-1]). Для данного выражения должно выполняться такое условие: -[Ri-1 / 2] <= Ri <= [Ri-1 / 2].
Вычислительная сложность
Вычислительной сложностью называется понятие в информатике при построении различных алгоритмов, которое обозначает некоторую функциональную зависимость объема работы от типа исходных данных. Для лемы Евклида она изучена полностью и эквивалентна произведению количества шагов деления на вычислительную сложность абстрактного вычислительного элемента.
Во время вычислительного процесса значение НОД записывается только в одно машинное слово. Алгоритм состоит из совокупности определенных шагов, каждый из которых занимает равные отрезки времени. Следовательно, они являются постоянными величинами. Количество шагов для расчета НОД (f, g) следует обозначить W (f, g).
Предположив, что s = НОД (f, g), можно воспользоваться введением некоторых целых коэффициентов m и n: f = m * s и g = n * s. В этом случае W (f, g) = W (m, n) уравнение можно разделить на s. Число шагов является постоянной величиной при умножении f и g на множитель L, т. е. W (f, g) = W (L * m, L * n). Следовательно, искомая переменная зависит от НОД.
Когда для вычисления по алгоритму требуется N шагов для чисел f > 0 и g > 0, должно выполняться такое неравенство с числами Фибоначчи Fn+2 и Fn+1 соответственно: f >= Fn+2 и g >= Fn+1. Доказывается данное утверждение при помощи математической индукции. Если предположить, что N = 1, то остаток отношения f / g эквивалентен 0.
Наименьшими значениями являются f = 2 и g = 1 (F2 и F3 соответственно). Предположим, что результат для значений на промежутке от N до М — 1. Первый шаг c M шагами записывается таким образом: f = Q0 * g + R0. Следовательно, выполнение алгоритма для чисел g и R0 (g > R0) требует (М — 1) шагов.
В результате этого получаются два нестрогих неравенства g >= Fm+1 и R0 >= Fm. Из выражения следует, что f = Q0 * g + R0 >= g + R0 >=Fm+1 + Fm = Fm+2. Данное доказательство было выполнено в 1844 году математиком Г. Ламе. Оно является главным элементом теории сложности вычислений. Формулировка данного утверждения следующая: при нахождении НОД f и g в результате деления с некоторым остатком число операций по алгоритму Евклида не превосходит 5.
Пример решения
Специалисты рекомендуют закрепить теоретические знания решением различных упражнений. Необходимо разобрать применение алгоритма на примере нахождения НОД (1071,462). Для этого следует действовать по такой инструкции, позволяющей решить простым способом задачу:
- Выполнить операцию разности до получения остатка: 1071 — 462 — 462 + 147 = 1071 — 2 * 462 + 147 (Q0 = 2, R0 = 147).
- От 462 отнять 147 до получения результата, который меньше 147: 462 — 147 — 147 — 147 + 21 = 462 — 3 * 147 + 21 (Q1 = 3, R1 = 21).
- Анализ пары чисел 147 и 21: 147 — 21 — 21 — 21 — 21 — 21 — 21 — 21 + 0 (Q2 = 7, R2 = 0).
- Определение результата: НОД (1071,462) = 21.
На третьем шаге алгоритм заканчивается, поскольку остаток отсутствует, т. е. R2 = 0. В написании программ применяется такой же принцип. Если даны три числа, то методика решения усложняется. Для этой цели применяется специальный онлайн-калькулятор.
Таким образом, алгоритм Евклида помогает за незначительное время найти НОД двух и более чисел.