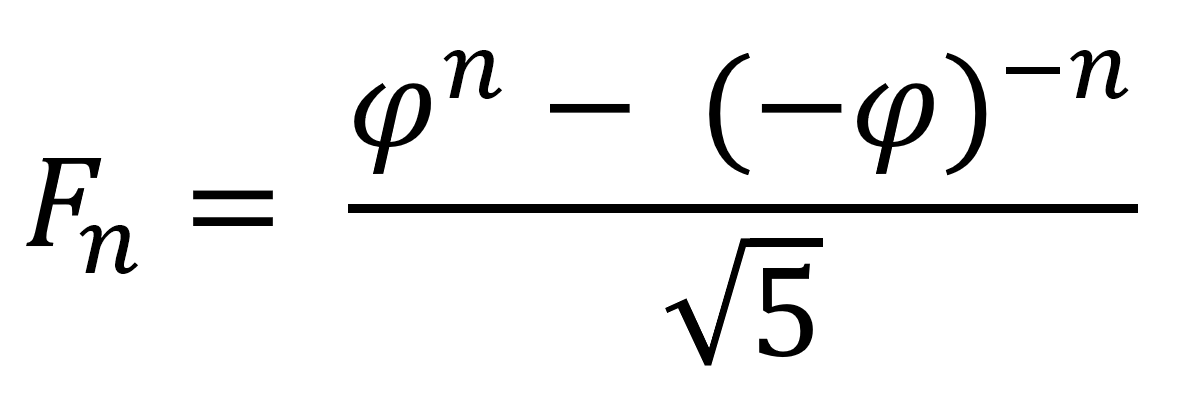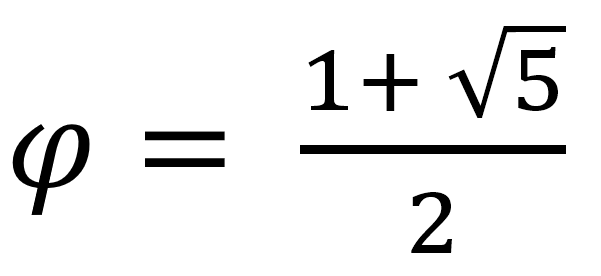Как найти ное число фибоначчи

Как я посчитал миллионное число Фибоначчи

Все мы понимаем, что рекурсивное вычисление чисел Фибоначчи крайне неэффективно. Многим людям наверняка хотелось проверить, где пределы (не)эффективности, но не доходили руки, не хватало времени. Специально к старту нового потока курса Fullstack-разработчик на Python мы решили поделиться переводом статьи, автор которой шаг за шагом показывает возможности современного Python на примере разных подходов к вычислению чисел Фибоначчи. В статье вы найдёте проблемные значения n и сравнение производительности оптимального и неоптимального решений на графике.

Нет, заголовок вообще не кликбейтный. Несколько дней назад я действительно хотел найти оптимальное решение для расчёта чисел Фибоначчи, хотелось попробовать вычислить стотысячное число последовательности, но я задумался; если я могу вычислить стотысячное число, то что остановит меня в поисках миллионного числа Фибоначчи? Сегодня я покажу, как шёл к вычислению и с какими проблемами столкнулся.

Последовательность Фибоначчи — одна из наиболее известных математических последовательностей и самый простой пример рекуррентных отношений. Каждое число последовательности — это сумма двух предыдущих чисел, начиная с 0 и 1. Получается такая последовательность:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее...

В следующие несколько минут я исследую несколько разных подходов, а затем покажу оптимальное решение:

1. Простая рекурсия.

2. Кеш с рекурсией.

3. Итеративный метод.

4. Формула Бине.

5. Расчёт 1000000-го числа Фибоначчи.

Но, прежде чем мы начнём, я должен сказать, что все упомянутые тайминги касаются оборудования, на котором я работаю сейчас, а версия Python — 3.9.1.

Простая рекурсия

Это очень простой способ получить N-ное число Фибоначчи на Python:

def recursiveFib(n):
    if n == 1 or n == 2:
        return 1

    return recursiveFib(n - 1) + recursiveFib(n - 2)

В коде используется рекурсия, он вызывает сам себя несколько раз, вычисляя предыдущее число и используя это число для вычисления следующего. Но это также недостаток, поскольку функция чрезвычайно неэффективна и ресурсоёмка: на каждом этапе она вычисляет предыдущие 2 числа, а также предыдущие 2 числа этих чисел и т. д.

Вскоре вы достигаете точки, когда вычисление следующего числа занимает слишком много времени, например, на моём компьютере мне потребовалось 1,43 секунды, чтобы вычислить 35-е число. Очевидно, что вычисление более высоких значений будет чрезвычайно медленным и практически невозможным.

Кеш с рекурсией

Поскольку мы постоянно вычисляем предыдущие 2 числа, для хранения числа можно воспользоваться возможностями кеширования, не нужно будет вычислять числа несколько раз. Встроенный модуль functools позволяет нам работать с LRU кешем; этот тип кеша организует элементы в порядке их использования. Такой подход может значительно ускорить процесс.

from functools import lru_cache

@lru_cache()
def recursiveFibCached(n):
    if n == 1 or n == 2:
        return 1

    return recursiveFibCached(n - 1) + recursiveFibCached (n - 2)

Во-первых, нам нужно импортировать декоратор lru_cache из модуля functools и поместить его перед нашей функцией. Мы можем указать значение maxsize, чтобы сообщить кешу, сколько элементов нужно хранить, но по умолчанию оно равно 128, это значение прекрасно работает. Используя кеш, мы можем вычислить 200-е число Фибоначчи всего за 0,0002252 секунды!

Одна проблема с использованием рекурсии заключается в том, что если вы попытаетесь вычислить 501-е число, то получите ошибку RecursionError: maximum recursion depth exceeded in comparison. Но, к счастью, проблему можно решить, установив большее значение глубины рекурсии:

import sys

sys.setrecursionlimit(5000)

Теперь мы можем вычислить 1000-е число Фибоначчи, на вычисление которого мне потребовалось всего 0,001198 секунды. Однако это создало для меня ещё одну проблему: по какой-то странной причине я не мог вычислить 1553-е число в последовательности, и даже после увеличения предела рекурсии ничего не произойдёт, ничего не будет распечатано на терминале, и программа просто закончит выполнение. Очевидно, что это проблема и недостаток на моём пути к вычислению миллионного числа Фибоначчи.

Итеративный метод

Вы можете увидеть, что применение рекурсивного решения проблемы в компьютерной науке часто рассматривается как халатность, а итеративные методы считаются намного лучше. Для генерации чисел Фибоначчи мы можем создать итеративное решение:

def iterativeFib(n):
    a, b = 0, 1

    for i in range(n):
        a, b = b, a + b

    return a

Мы можем воспользоваться им, чтобы вычислить любое число Фибоначчи (я не тестировал подход с особенно большими числами), и часто этот подход работает также очень быстро, 1000-е число вычислилось всего за 0,0028195 секунды.

Вы можете задаться вопросом, почему нельзя воспользоваться этим подходом для вычисления 1000000-го числа, и да, это возможно, но займёт немного времени. Продолжайте читать, и я расскажу, почему.

Формула Бине

Формула Бине — это формула, которая может использоваться для вычисления n-го члена последовательности Фибоначчи, а это именно то, что мы хотим сделать; эта формула названа в честь открывшего её французского математика Жака Филиппа Мари Бине. Вот она:

Вы можете заметить греческую букву PHI (ϕ), она означает золотое сечение:

Можно написать формулу на Python и сразу же начать работать с ней:

def formulaFib(n):
    root_5 = 5 ** 0.5
    phi = ((1 + root_5) / 2)

    a = ((phi ** n) - ((-phi) ** -n)) / root_5

    return round(a)

Примечание: для реализации на Python нам нужно вернуть округление вычисляемого числа, потому что при вычислении большого числа Python вернёт результат, в котором может быть более двадцати девяток после запятой.

Всё это хорошо, так как теперь у нас нет никаких циклов и мы можем мгновенно вычислить ответ, верно? Что ж, в этом методе есть небольшая загвоздка. Если мы попытаемся вычислить что-либо выше 1475-го числа, то столкнёмся с ошибкой: OverflowError: (34, result too large). Это связано с тем, как в python реализованы числа с плавающей точкой, они могут иметь конкретное максимальное значение, которое мы превышаем, когда используем этот метод.

Однако исправить ситуацию очень легко. Мы можем использовать встроенный модуль под названием decimal, чтобы создать десятичный объект с гораздо более высокой точностью и подходящим для работы с уравнением размером:

import decimal

def formulaFibWithDecimal(n):
    decimal.getcontext().prec = 10000

    root_5 = decimal.Decimal(5).sqrt()
    phi = ((1 + root_5) / 2)

    a = ((phi ** n) - ((-phi) ** -n)) / root_5

    return round(a)

В этой новой функции мы устанавливаем значение точности длиной 10000 цифр, преобразуем наше значение квадратного корня из 5 в десятичное значение объекта и используем его в нашем уравнении. Это позволяет нам легко вычислить 10000-е число в последовательности за поразительные 0,0692986 секунды, а это по сравнению со всеми нашими предыдущими методами огромное улучшение.

Расчёт 1000000-го числа Фибоначчи

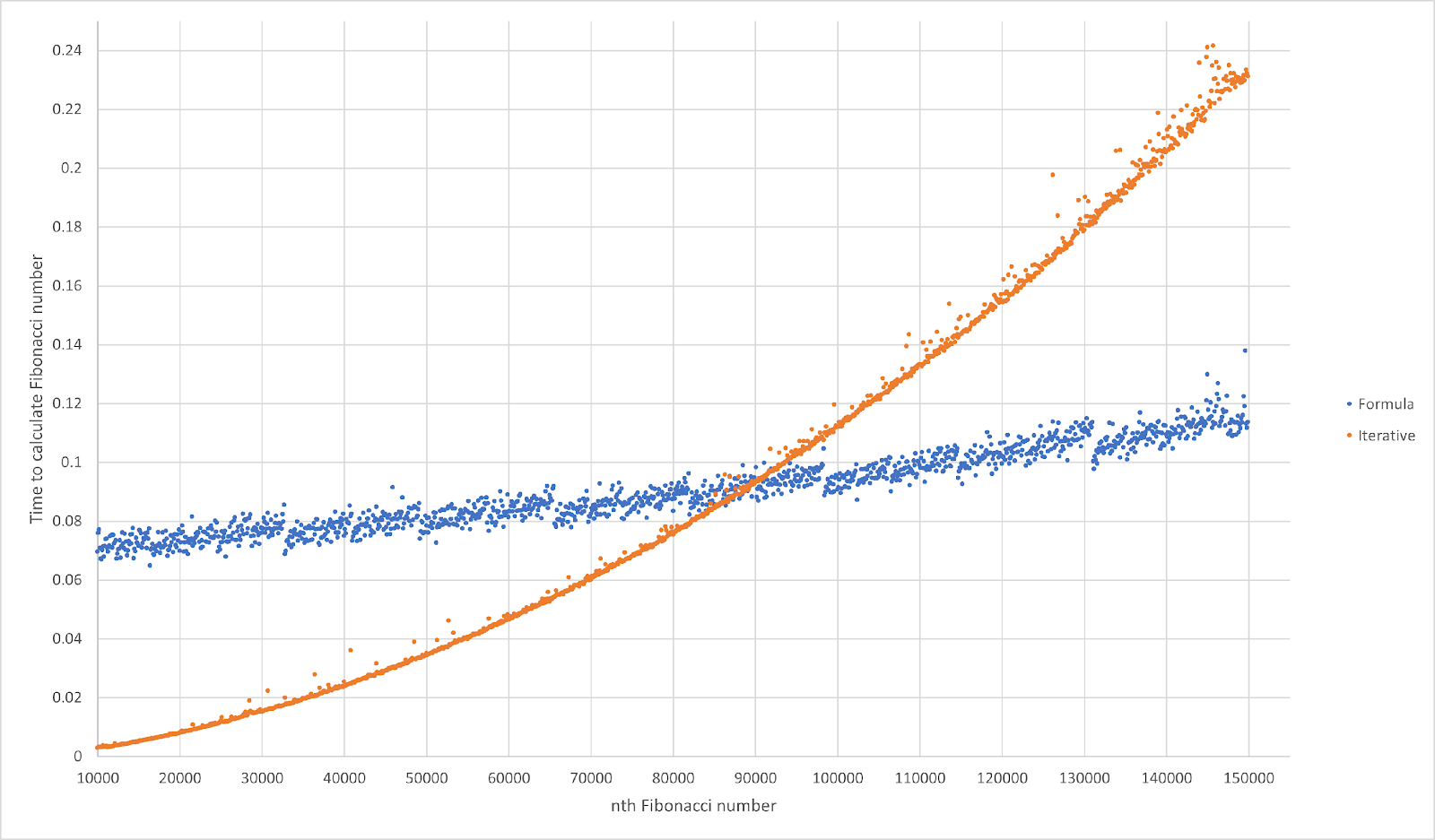
Теперь вы, возможно, заметили, что формула работает медленнее итерационного решения, когда n=10000. Это связано с тем, что в формуле нам нужно создать десятичный объект и использовать его в уравнении, этот процесс занимает больше времени, чем повторение одной простой инструкции 10000 раз. Но история ещё не окончена.

Увеличение количества циклов может радикально увеличить длительность всего процесса. В какой-то момент, когда n составляет приблизительно 89200, время, необходимое итеративному решению для вычисления ответа, равно времени, которое необходимо при вычислении по формуле; когда же n увеличивается, время выполнения итеративного алгоритма возрастает с большей скоростью, чем время на решение по формуле.

На графике видно точку пересечения времени выполнения формулы и итерационных графиков. Исходя из этого мы можем сказать, что с увеличением n время вычисления числа Фибоначчи по формуле возрастает линейно. Но при итеративном решении время увеличивается с увеличением n. Это даёт нам понять, что для вычисления миллионного числа Фибоначчи нам нужно использовать формулу. Дополнительное изменение, которое я должен был сделать, чтобы правильно вычислить число, — увеличить точность моего десятичного объекта строкой кода decimal.getcontext().prec = 300000.

Ваше время выполнения алгоритма может отличаться. На моём компьютере, чтобы вычислить 1000000-е число Фибоначчи, потребовалось:

• 8,832661 секунды при решении с итерацией;

• 1,151380 секунды с формулой Бине, это в 7,7 раза быстрее!

Если вам хочется узнать число, оно состоит из 208988 цифр и в текстовом файле занимает 209 КБ:

Заключение

Вот так я вычислил миллионное число Фибоначчи, конечно, я мог бы вычислить число больше, но на самом деле для этого нет никакой реальной причины, и это заняло бы много времени, даже с использованием формулы Бине. Из приведённого выше графика я могу оценить затраты времени: чтобы вычислить миллиардное число Фибоначчи, мне потребуется примерно 310,8467 секунды, я оставлю это читателям. А чтобы получить специальность Fullstack-разработчик на Python — потребуется немногим более года. Но можно и быстрее — на нашем курсе студенты не привязаны к программе и скорость их прогресса зависит от них самих.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering

Другие профессии и курсы

Задача: посчитать N-е число последовательности, в которой каждый элемент равен сумме двух предыдущих. Такая последовательность называется последовательностью Фибоначчи: 1, 1, 2, 3, 5, 8…

Очень часто на разнообразных олимпиадах попадаются задачи вроде этой, которые, как думается на первый взгляд, можно решить с помощью простого перебора. Но если мы подсчитаем количество возможных вариантов, то сразу убедимся в неэффективности такого подхода: например, простая рекурсивная функция, приведенная ниже, будет потреблять существенные ресурсы уже на 30-ом числе Фибоначчи, тогда как на олимпиадах время решения часто ограничено 1-5 секундами.

int fibo(int n)
{
    if (n == 1 || n == 2) {
        return 1;
    } else {
        return fibo(n - 1) + fibo(n - 2);
    }
}

Давайте подумаем, почему так происходит. Например, для вычисления fibo(30) мы сначала вычисляем fibo(29) и fibo(28). Но при этом наша программа «забывает», что fibo(28) мы уже вычисляли при поиске fibo(29).

Основная ошибка такого подхода «в лоб» в том, что одинаковые значения аргументов функции исчисляются многократно — а ведь это достаточно ресурсоемкие операции. Избавиться от повторяющихся вычислений нам поможет метод динамического программирования — это прием, при использовании которого задача разбивается на общие и повторяющиеся подзадачи, каждая из которых решается только 1 раз — это значительно повышает эффективность программы. Этот метод подробно описан в нашей статье, там же есть и примеры решения других задач.

Самый просто вариант улучшения нашей функции — запоминать, какие значения мы уже вычисляли. Для этого нужно ввести дополнительный массив, который будет служить как бы «кэшем» для наших вычислений: перед вычислением нового значения мы будем проверять, не вычисляли ли его раньше. Если вычисляли, то будем брать из массива готовое значение, а если не вычисляли — придётся считать его на основе предыдущих и запоминать на будущее:

int cache[100];

int fibo(int n)
{
    if (cache[n] == 0) {
        if (n == 1 || n == 2) {
            cache[n] = 1;
        } else {
            cache[n] = fibo(n - 1) + fibo(n - 2);
        }
    }

    return cache[n];
}

Так как в данной задаче для вычисления N-ого значения нам гарантированно понадобится (N-1)-е, то не составит труда переписать формулу в итерационный вид — просто будем заполнять наш массив подряд до тех пор, пока не дойдём до нужной ячейки:

cache[0] = 1;
cache[1] = 1;

for (int i = 2; i <= n; i++) {
    cache[i] = cache[i - 1] + cache[i - 2];
}

cout << cache[n-1];

Теперь мы можем заметить, что когда мы вычисляем значение F(N), то значение F(N-3) нам уже гарантированно никогда не понадобится. То есть нам достаточно хранить в памяти лишь два значения — F(N-1) и F(N-2). Причём, как только мы вычислили F(N), хранение F(N-2) теряет всякий смысл. Попробуем записать эти размышления в виде кода:

//Два предыдущих значения:
int cache1 = 1;
int cache2 = 1;
//Новое значение
int cache3;

for (int i = 2; i <= n; i++) {
    cache3 = cache1 + cache2; //Вычисляем новое значение

    //Абстрактный cache4 будет равен cache3+cache2
    //Значит cache1 нам уже не нужен?..

    //Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации.
    //cache5 = cache4 - cache3 => через итерацию потеряет актуальность cache2, т.е. он и должен стать cache1

    //Иными словами, cache1 -- f(n-2), cache2 -- f(n-1), cache3 -- f(n).
    //Пусть N=n+1 (номер, который мы вычисляем на следующей итерации). Тогда n-2=N-3, n-1=N-2, n=N-1.
    //В соответствии с новыми реалиями мы и переписываем значения наших переменных:

    cache1 = cache2;
    cache2 = cache3;
}

cout << cache3;

Бывалому программисту понятно, что код выше, в общем-то ерунда, так как cache3 никогда не используется (он сразу записывается в cache2), и всю итерацию можно переписать, используя всего одно выражение:

cache[0] = 1;
cache[1] = 1;
 
for (int i = 2; i <= n; i++) {
    cache[i%2] = cache[0] + cache[1];
    //При i=2 устареет 0-й элемент
    //При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый
    //При i=4 последним элементом мы обновляли cache[1], значит ненужное старьё сейчас в cache[0]
    //Интуитивно понятно, что так будет продолжаться и дальше
}
 
cout << cache[n%2];

Для тех, кто не может понять, как работает магия с остатком от деления, или просто хочет увидеть более неочевидную формулу, существует ещё одно решение:

int x = 1;
int y = 1;

for (int i = 2; i < n; i++) {
   y = x + y;
   x = y - x;
}

cout << "Число Фибоначчи: " << y;

Попробуйте проследить за выполнением этой программы: вы убедитесь в правильности алгоритма.

P.S. Вообще, существует единая формула для вычисления любого числа Фибоначчи, которая не требует никаких итераций или рекурсии:

const double SQRT5 = sqrt(5);
const double PHI = (SQRT5 + 1) / 2;

int fibo(int n){
    return int(pow(PHI, n) / SQRT5 + 0.5);
}

Но, как можете догадаться, подвох в том, что цена вычисления степеней нецелых чисел довольно велика, как и их погрешность.

Была ли эта статья полезной?