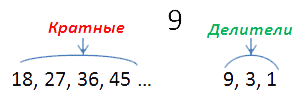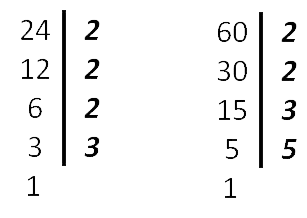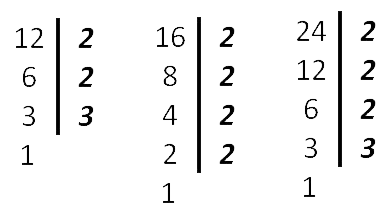Наименьшее о́бщее кратное (HOK) двух целых чисел — это наименьшее натуральное число, которое делится на оба без остатка, то есть кратно им обоим. К примеру, для чисел 6 и 4, наименьшим общим кратным будет 12.
Как найти НОК?
Способов найти НОК несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОК при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители;
- выбрать одну группу множителей;
- добавить к ним множители из второй группы, которые отсутствуют в выбранной;
- найти их произведение.
Примеры нахождения наименьшего общего кратного
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОК 4 и 6
1. Раскладываем 6 и 4 на простые множители:
2. Возьмем первую группу множителей: 2 · 3.
3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 3 · 2 = 12.
Ответ: НОК (6; 4) = 12
Пример 2: найти НОК 32 и 20
1. Раскладываем 32 и 20 на простые множители:
2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.
3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.
Ответ: НОК (32; 20) = 160
Наименьшее общее кратное: как найти
Содержание:
- Наименьшее общее кратное — что это такое
- Вычисление НОК, правила в математике
- Как найти НОК через НОД
- Как найти НОК через разложение чисел
- Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное — что это такое
Определение
Число, которое можно без остатка разделить на выбранные числа, является их общим кратным. Наименьшее из таких чисел — наименьшее общее кратное или сокращенно «нок».
Действия с дробями, имеющими различный знаменатель, можно значительно облегчить, если найти наименьшее общее кратное (НОК). Это такое число, например, кратное числу а, которое можно разделить на это а целиком, без остатка.
Пример
К числам, кратным 8, относятся 16, 24, 32, 40 и т.п. Кратными 9-ти являются 9, 18, 27, 36 и т.п.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Существует бесчисленное множество чисел, делящихся на а без остатка, т.е. кратных ему. В то же время, этого нельзя сказать о числе делителей. Так, делителями для 9-ти являются 9, 3, 1.
Если для двух или более натуральных чисел существует число, делящееся на оба без остатка, то оно является наименьшим общим кратным. А то из, них, которое самое маленькое, является нок.
Вычисление НОК, правила в математике
Для нахождения нок в математике существует несколько правил или алгоритмов. Самый простой вариант — вычисление НОК для двух чисел-участников. Способ легкий, но приемлем для маленьких натуральных чисел.
Нужно составить ряды чисел, кратных каждому из выбранных значений.
Пример
К (4) — 4, 8, 12, 16, 20, 24;
К (6) — 6, 12, 18, 24, 30.
Из рядов видно, что в обоих рядах встречаются числа 12 и 24. Это общие кратные. Однако 12 из них — меньшее число.
Поэтому НОК (4, 6) — 12.
Как найти НОК через НОД
Определение НОК можно провести с использованием НОД (наибольшего общего делителя).
В этом блоке изложения материала следует уточнить некоторые понятия.
Определение
Простым называется такое натуральное число, которое целиком можно разделить только само на себя либо на единицу.
Наименьшим простым числом является двойка. Она же — единственное четное натуральное простое число. Все остальные — нечетные.
Множество чисел делятся не только на 1 и на себя, но и на другие целые натуральные числа:
8 делится на 1, 2, 4, 8;
36 — на 1, 2, 3, 4, 6, 8 и т.д.
Эти числа — делители восьми и тридцати шести (делимых). Именно они могут разделить 8 и 36 без остатка. В обоих приведенных примерах делимые (8, 36) являются составными числами, поскольку имеют более двух делителей.
В приведенных рядах существуют одинаковые делители. Это 1, 2, 4, 8.
Самое большое число — 8. Оно и является наибольшим общим делителем.
Определение
Наибольший общий делитель (НОД) — число, на которое без остатка делится выбранная пара (либо больше) чисел.
Пример
НОД (9, 45)=9
НОД (12, 48)=12
Бывают пары чисел, которые из общих делителей имеют только единицу. Тогда они называются взаимно простыми: НОД (9, 8)=1, НОД (12, 10)=1.
На следующем примере показаны пары чисел со значениями их НОД и НОК.
Решение задачи по нахождению НОК через НОД сводится к следующей формуле:
НОК чисел a,b равняется частному произведения a и b на наибольший общий делитель чисел a и b (по-другому НОД (a, b).
Исходя из этого заключения получается, что НОК и НОД взаимосвязаны друг с другом. Наименьшее общее кратное можно легко найти через наибольший общий делитель для двух или более натуральных чисел.
Как найти НОК через разложение чисел
Кроме составления рядов значений, кратных каждому из двух выбранных натуральных чисел, для правильного определения НОК пользуются методом разложения на множители.
Найденные простые множители первого разложения сравниваются с аналогичными из второго разложения, после чего они перемножаются.
Пример
После разложения числа 9 на простые множители получается ряд:
1, 3, 9.
После разложения 12-ти получается ряд:
1, 2, 3, 4, 6, 12.
После разложения на множители числа 9 получаем: 3*3. После разложения на множители 12-ти получаем: 2*2*3. Объединяя множители обеих вариантов, получаем произведение: 3*3*2*2=36.
Наименьшее общее кратное чисел 9 и 12 — 36.
В качестве проверки произведем действия:
- 36/12=3
- 9/3=3
На практике записывают: НОК (9, 12)=36.
Такими действиями можно найти НОК более сложных чисел.
Пример
Найти НОК чисел 50 и 180.
Число 50 делится на 1, 2, 5, 10, 25, 50.
Число 180 на: 1, 5, 15, 30, 45, 90, 180.
Разложив на множители 50, получаем: 2, 5, 5.
Разложив 180, получаем: 2, 2, 3, 3, 5.
Из первого разложения выписываем: 2*5*5. Сравнивая со вторым разложением, описываем одну двойку и две тройки. После перемножения полученного ряда получается произведение: 2*5*5*2*3*3=900. Это и есть наименьшее общее кратное чисел 50 и 180.
Следовательно, НОК (50, 180)=900.
Существует еще один быстрый способ находить НОК. Он приемлем для вариантов, когда одно число нацело делится на другое. Например: НОК (15, 30)=30, НОК (20, 80)=80, НОК (16, 48)=48.
Для случаев, когда у двух чисел не имеется общих делителей, их можно просто перемножить и получить НОК. Например, НОК (7, 8)=56, НОК (4, 9)=36, НОК (7, 9)=63.
Нахождение НОК трех и большего количества чисел
Если предстоит найти НОК для большего, чем 2, количества чисел, их нужно разложить на простые множители. Например,
32=2*2*2*2*2;
40=2*2*2*5;
80=2*2*2*2*5
Сравнивая множители в каждом случае разложения натуральных чисел и выстраивая их в один ряд для умножения, получаем, что НОК (32, 40, 80) = 2*2*2*2*2*5 = 160.
В математике принято для нахождения НОК трех и более чисел применять следующую теорему:
Если имеется ряд чисел (а1, а2, а3…аk), можно найти НОК mk этих чисел производя последовательные вычисления: m2=НОК (а1, а2), m3=НОК (а2, а3)… mk=НОК (mk-1, аk)
Пример
Дано задание вычислить НОК для чисел 140 (a1), 9 (a2), 54 (а3), 250 (а4).
Тогда m2=НОК (a1, a2)=НОК (140, 9).
Для нахождения НОК (140, 9) производим действия. 140=15*9+5; 9=5*1+4.
Последующее разложение: 5=4*1+1, 4=4*1.
Следовательно, НОД (140, 9)=1. НОК (140, 9)=140*9/НОД (140, 9)=140*9/1=1260.
Ответ: m2=1260
По аналогии вычисляем m3 (=3780) и m4 (=94500). Это и есть ответ решения задачи по нахождению НОК чисел 140, 9, 54, 250.
Для того, чтобы находить общий знаменатель
при
сложении
и
вычитании дробей с разными
знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу «a» — это число, которое
само делится на число «a» без остатка.
Числа кратные 8
(то есть, эти числа разделятся на 8 без остатка):
это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей
этого же числа. Делителей —
конечное количество.
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Запомните!
Наименьшим общим кратным (НОК) двух и более натуральных
чисел называется наименьшее натуральное число, которое само
делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
- Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое
для обоих чисел. - Кратное числа «a»
обозначаем большой буквой «К».К (a) = {…, …}
Пример. Найти НОК 6 и 8.
К (6) = {12, 18, 24, 30, …}
К (8) = {8, 16, 24, 32, …}
НОК (6, 
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
- Разложить данные числа на простые множители.
Подробнее правила разложения на
простые множители вы можете прочитать в теме
как найти наибольший общий делитель (НОД).
- Выписать в строчку множители, входящие в разложение
самого большого из чисел, а под ним —
разложение остальных чисел.Запомните!
Количество одинаковых множителей в разложениях чисел может быть разное.
60 = 2 · 2 · 3 · 5
24 = 2 · 2 · 2 · 3
- Подчеркнуть в разложении
меньшего числа (меньших чисел) множители,
которые не вошли в разложение бóльшего числа
(в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2 - Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).
24 = 2 · 2 · 2 · 3
16 = 2 · 2 · 2 · 2
12 = 2 · 2 · 3
Как видим из разложения чисел, все множители 12 вошли в
разложение 24
(самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из
разложения числа 16.
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
- Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60
- Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее
кратное равно произведению этих чисел.Пример.
НОК (8, 9) = 72
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
5 сентября 2020 в 15:37
Елена Елена
Профиль
Благодарили: 0
Сообщений: 1
Елена Елена
Профиль
Благодарили: 0
Сообщений: 1
НОК(360,102)
0
Спасибо
Ответить
6 сентября 2020 в 13:42
Ответ для Елена Елена
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
360 = 23 · 32 · 5; 102 = 2 · 3 · 17.
НОК(360; 102) = 23 · 32 · 5 · 17 = …
0
Спасибо
Ответить
30 мая 2018 в 17:34
Тамара Татарникова
Профиль
Благодарили: 0
Сообщений: 1
Тамара Татарникова
Профиль
Благодарили: 0
Сообщений: 1
Найдите четырёхзначное число, которое кратно 24, а произведение цифр этого числа равно 16, в ответ дайте какое-нибудь одно число.
Я написала 1242, но 1242 при делении на 24 дает в ответе 51,75 будет ли это верным ответом?
0
Спасибо
Ответить
3 июня 2018 в 1:58
Ответ для Тамара Татарникова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
1128 1224 8112
0
Спасибо
Ответить
29 ноября 2016 в 14:47
Анвар Тынайбеков
Профиль
Благодарили: 0
Сообщений: 1
Анвар Тынайбеков
Профиль
Благодарили: 0
Сообщений: 1
НОК(344и170)=
0
Спасибо
Ответить
2 декабря 2016 в 8:23
Ответ для Анвар Тынайбеков
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1
Спасибо
Ответить
15 февраля 2016 в 19:02
Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
число 123 454 321 делится на 11 111. найдите нок этих чисел
1
Спасибо
Ответить
15 февраля 2016 в 19:08
Ответ для Кирилл Журавлёв
Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
12132211
0
Спасибо
Ответить
19 сентября 2016 в 12:55
Ответ для Кирилл Журавлёв
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Здесь подробно описано нахождение НОК.
А в супер-решателе можно себя проверить.
0
Спасибо
Ответить
15 февраля 2016 в 18:51
Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
ЧИСЛО 123 454 321 ДЕЛИТСЯ 11 111. НАЙДИТЕ НОК ЭТИХ ЧИСЕЛ НЕ ВЫПОЛНЯЯ РАЗЛОЖЕНИЯ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ
0
Спасибо
Ответить
19 сентября 2016 в 12:56
Ответ для Кирилл Журавлёв
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
27 января 2016 в 18:15
Lera Kuchinskaya
Профиль
Благодарили: 0
Сообщений: 1
Lera Kuchinskaya
Профиль
Благодарили: 0
Сообщений: 1
НОК 100 150 250
0
Спасибо
Ответить
27 января 2016 в 22:36
Ответ для Lera Kuchinskaya
Виктория Казимирова
Профиль
Благодарили: 0
Сообщений: 1
Виктория Казимирова
Профиль
Благодарили: 0
Сообщений: 1
А что за цифры!!!?
0
Спасибо
Ответить
28 января 2016 в 16:00
Ответ для Lera Kuchinskaya
Anton Wuckert
Профиль
Благодарили: 0
Сообщений: 1
Anton Wuckert
Профиль
Благодарили: 0
Сообщений: 1
НОК = 1500
0
Спасибо
Ответить
19 сентября 2016 в 11:42
Ответ для Lera Kuchinskaya
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для решения можно воспользоваться решателем на сайте.
0
Спасибо
Ответить
22 января 2016 в 13:46
Андрей Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Андрей Алексеев
Профиль
Благодарили: 0
Сообщений: 1
числа 4,5,6,7,10,12,15,16,20,50, которые являются делителями 24 и кратными 2
0
Спасибо
Ответить
23 января 2016 в 13:33
Ответ для Андрей Алексеев
Александра Сирота
Профиль
Благодарили: 0
Сообщений: 2
Александра Сирота
Профиль
Благодарили: 0
Сообщений: 2
ОТВЕТ: 4 и 12
0
Спасибо
Ответить
24 января 2016 в 13:41
Ответ для Андрей Алексеев
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
6 ,2, 12
0
Спасибо
Ответить
25 января 2016 в 19:52
Ответ для Андрей Алексеев
Нелия Ахмедова
Профиль
Благодарили: 0
Сообщений: 1
Нелия Ахмедова
Профиль
Благодарили: 0
Сообщений: 1
6,12.
0
Спасибо
Ответить
19 сентября 2016 в 10:59
Ответ для Андрей Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Чтобы не запутаться, необходимо каждое из чисел проверить на оба условия:
1) 4 — 24/4=6 — делитель 24. 4/2=2 — кратно 2.
2) 5 — 24/5=не делится без остатка — не делитель. 5/2 — не делится без остатка — не кратно 2.
И так далее.
Ответ: 4,6,12.
0
Спасибо
Ответить
23 декабря 2015 в 17:00
Евгений Мухамедшин
Профиль
Благодарили: 0
Сообщений: 1
Евгений Мухамедшин
Профиль
Благодарили: 0
Сообщений: 1
1) (4/15+5/8)-3/5
2) (1/5+13/16)-9/20
0
Спасибо
Ответить
19 сентября 2016 в 10:01
Ответ для Евгений Мухамедшин
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для нахождения НОК можно воспользоваться супер-решателем. Раскрываем скобки и приводим к общему знаменателю.
1) ===0
2) ===
0
Спасибо
Ответить
17 ноября 2015 в 6:29
Светлана Каблучко
Профиль
Благодарили: 0
Сообщений: 1
Светлана Каблучко
Профиль
Благодарили: 0
Сообщений: 1
запишите числа удовлетворяющие двойное неравенство 354<х<361 если известно что они кратны 2,5,10
0
Спасибо
Ответить
24 ноября 2015 в 17:56
Ответ для Светлана Каблучко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
360
0
Спасибо
Ответить
Математика
5 класс
Урок № 44
Наименьшее общее кратное (НОК)
Перечень рассматриваемых вопросов:
– делители числа;
– кратные числа;
– признаки делимости;
– разложение на простые множители;
– НОК.
Тезаурус
Кратное число – это число, делящееся на данное целое число без остатка.
Простое число – это такое натуральное число, которое больше 1 и делится только на 1 и само на себя.
Составные числа – это непростые натуральные числа, большие 1.
Взаимно простые числа – это числа, которые не имеют общих простых делителей
Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Ранее мы узнали, что такое кратное, ввели понятие делителя, научились находить наибольший общий делитель, а можно ли каким-либо способом найти общее кратное нескольких чисел? Оказывается, можно, этим сегодня мы и будем заниматься. Но находить не просто общее кратное нескольких чисел, а их наименьшее общее кратное – НОК.
Итак, для начала вспомним, что называется кратным. Это число, делящееся на данное натуральное число без остатка.
Теперь найдём, например, общие кратные чисел 12 и 15. Для этого выпишем все кратные чисел 12 и 15.
12 – его кратные 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …
15 – его кратные 15, 30, 45, 60, 75, 90, 105, 120, 135, …
Из представленных чисел общие кратные – это числа 60 и 120. Меньшее из них – 60. Это и есть наименьшее общее кратное чисел.
Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.
Для нахождения наименьшего общего кратного двух чисел можно использовать несколько способов. Один из них мы рассмотрели на примере нахождения НОК 12 и 15. Этот способ заключается в том, что выписываются все кратные двух чисел и затем находится наименьший общий из них.
Узнаем ещё одно правило нахождения НОК.
Во-первых, разложим числа на простые множители. Далее подчеркнём одинаковые множители этих чисел. Затем перемножим общие множители одного из чисел и добавим произведение всех остальных множителей от каждого числа. Это и будет НОК заданных чисел.
Найдём НОК (15; 16). Разложим числа на простые множители:
Видно, что из всех множителей общий лишь единица, значит, это взаимно простые числа.
НОК взаимно простых чисел – это произведение всех их множителей или произведение этих чисел.
В данном случае НОК равен 240.
Т. е. НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.
Найдём НОК (10; 100). Разложим числа на простые множители:
Выделим общие делители у этих чисел, это 2 и 5.
Умножим их, а результат умножим ещё на оставшиеся простые множители от чисел 100 и 10.
НОК (10; 100) = 2 · 5 · 2 · 5 = 100
Обратите внимание на то, что 100 делится нацело на 10, и НОК тоже равен 100. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОК этих чисел равен большему из них.
Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом. Например, рассмотрим такую задачу.
Девочка решила купить несколько плиток шоколада по 38 руб. , но у неё только 5-рублёвые монеты, а в магазине нет сдачи. Какое наименьшее количество плиток шоколада она сможет купить?
Решение: чтобы решить эту задачу, нужно найти НОК (5;38).
Разложим числа на множители:
Мы видим, что НОК (5; 38) = 5 · 38 = 190 – это будет сумма покупки за шоколад.
Теперь найдём, сколько девочка купит плиток.
Для этого сумму покупки разделим на стоимость одной плитки шоколада.
190 : 38 руб. = 5 – наименьшее количество плиток шоколада, которые сможет купить девочка.
Ответ: 5 плиток.
Тренировочные задания
№ 1. Какую цифру нужно подставить в число НОК (7; 2_) вместо пропуска, чтобы получить НОК = 21?
Варианты ответов: 1; 2; 3.
Решение: для решения этой задачи, надо разложить на множители оба числа, при этом вместо пропуска нужно подставить по порядку все цифры. А далее найти подходящий НОК этих чисел, равный 21.
Из всех разложений на множители под НОК (7; 2_) = 21 подходит только число 21.
НОК (7; 21) =21
НОК (7; 22) =154
НОК (7; 23) =161
Ответ: искомая цифра – 1.
№ 2. Какой наименьшей длины должен быть рулон ткани, чтобы от него без остатка можно было отрезать куски по 3 м и 7 м?
Решение: чтобы решить эту задачу, нужно найти НОК заданных чисел, он и будет являться искомым ответом, т. е. наименьшей длиной рулона ткани.
НОД (3; 7) = 7 · 3 = 21 м
Ответ: 21 м.
Наименьшее общее кратное
- Общее кратное
- Наименьшее общее кратное
- Как найти НОК
- С помощью разложения на простые множители
- Нахождение НОК через НОД
- Калькулятор НОК
Общее кратное
Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.
Пример.
Числу 3 кратны числа: 6, 9, 12, 15 и т. д.
Числу 4 кратны числа: 8, 12, 16, 20 и т. д.
Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.
Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.
Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.
Пример. Найти общее кратное для чисел 2, 3, 4, 6.
Решение:
2 · 3 · 4 · 6 = 144.
Число 144 — общее кратное чисел 2, 3, 4 и 6.
Для любого количества натуральных чисел существует бесконечно много кратных.
Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.
Наименьшее общее кратное
Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.
Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.
Наименьшее общее кратное записывается так:
НОК (a, b, …) = x.
Числа в круглых скобках могут быть указаны в любом порядке.
Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:
НОК (3, 4, 9) = 36.
Как найти НОК
Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.
С помощью разложения на простые множители
Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: разложим каждое из этих чисел на простые множители:
99 = 3 · 3 · 11 = 32 · 11,
54 = 2 · 3 · 3 · 3 = 2 · 33.
Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.
Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:
2 · 33 · 11 = 594.
Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.
Ответ: НОК (99, 54) = 594.
Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.
Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.
Решение: разложим каждое из этих чисел на простые множители:
12 = 2 · 2 · 3 = 22 · 3,
49 = 7 · 7 = 72.
Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:
22 · 3 · 72 = 12 · 49 = 588.
Ответ: НОК (12, 49) = 588.
Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.
Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.
Решение: так как данные числа являются простыми, то просто перемножим их:
5 · 7 · 13 = 45.
Ответ: НОК (5, 7, 13) = 455.
Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.
Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.
Решение: разложим каждое из этих чисел на простые множители:
24 = 2 · 2 · 2 · 3 = 23 · 3,
12 = 2 · 2 · 3 = 22 · 3,
4 = 2 · 2 = 22.
Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:
23 · 3 = 24.
Ответ: НОК (24, 12, 4) = 24.
Нахождение НОК через НОД
НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.
Правило в общем виде:
НОК (m, n) = m · n : НОД (m, n)
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: сначала находим наибольший общий делитель:
НОД (99, 54) = 9.
Теперь мы можем вычислить НОК этих чисел по формуле:
НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.
Ответ: НОК (99, 54) = 594.
Чтобы найти НОК трёх или более чисел используется следующий порядок действий:
- Находят НОК любых двух из данных чисел.
- Затем находят наименьшее общее кратное найденного НОК и третьего числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.
Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:
НОД (12, 
Вычисляем их НОК по формуле:
НОК (12, 

Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:
НОД (24, 9) = 3.
Вычисляем НОК по формуле:
НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.
Ответ: НОК (8, 12, 9) = 72.
Калькулятор НОК
Данный калькулятор поможет вам найти наименьшее общее кратное чисел. Просто введите числа через пробел или запятую и нажмите кнопку Вычислить НОК
.