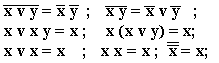23. Черный «Бьюик». 24. Третий учащийся изучал логику. 25. Сидоров. 29. а) нет; б) да; в) нет.
Определение. Прямым (декартовым) произведением множеств
|
~ |
= A1 |
× A2 |
×K× An ) называется |
|
A1 , A2 , K, An (обозначается A |
|||
|
множество всех векторов (a1 , a2 , K, an ) |
таких, что ai Ai , 1 ≤ i ≤ n . |
Если все множества Ai совпадают и равны A , то используют
обозначение An = A × A ×K× A .
1442443
n раз
Основные понятия и факты, связанные с булевым кубом
В дальнейшем в качестве множества Ai будет использоваться множество E2 ={0, 1}.
Определение. Набор (α1 , α2 , K, αn ) , где αi {0, 1}, 1 ≤ i ≤ n ,
называется булевым или двоичным набором (вектором). Элементы набора называют компонентами или координатами. Число n
|
~ |
~ n |
. |
|||||
|
называют длиной набора. Кратко (α1 , K, αn ) обозначают α |
или α |
||||||
|
~ n |
называют число его координат, равных |
||||||
|
Весом (или нормой) набора α |
|||||||
|
~ n |
n |
~ |
n |
n−k |
|||
|
|| = ∑αi . Число ν |
называют номером |
||||||
|
1, т.е. ||α |
(α) = ∑αk 2 |
||||||
|
~ |
i=1 |
k =1 |
|||||
|
набора α . |
Замечание. Набор (α1 , K, αn ) есть разложение числа ν(σ~) в двоичной системе и находится следующим образом: а) делим ν(σ~) на 2, остаток есть αn частное σ n ; б) делим σ n на 2, остаток есть αn−1 частное σn−1 ; и т. д. до тех пор пока не получим частное, равное 0.
|
~ n |
длины n |
||||||
|
Определение. Множество всех булевых векторов α |
|||||||
|
называется n -мерным кубом ( E2n = E2 ×K× E2 ). Сами векторы |
|||||||
|
14243 |
|||||||
|
n раз |
|||||||
|
называются вершинами n -мерного куба. |
|||||||
|
Кроме обозначения E2n |
для n -мерного куба используют обозначение |
||||||
|
B |
n |
~ n |
B |
n |
называют вершинами куба B |
n |
. |
|
, а наборы α |
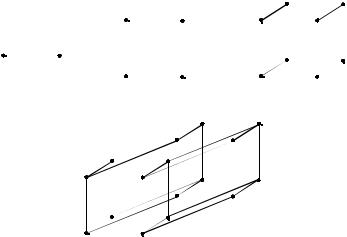
Геометрическая реализация. На рисунке 1.1. изображены проекции, соответственно, 1-мерного, 2-мерного, 3-мерного и 4-мерного кубов на плоскость.
|
1,1,0 |
1,1,1 |
||||||||||||||||||||||
|
0 |
1 |
1,0 |
1,1 |
0,1,0 |
0,1,1 |
||||||||||||||||||
|
1,0,0 |
1,0,1 |
||||||||||||||||||||||
|
0,0 |
0,1 |
||||||||||||||||||||||
|
E1 |
|||||||||||||||||||||||
|
2 |
E2 |
0,0,0 |
E3 |
0,0,1 |
|||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
|
1,1,1,0 |
1,1,1,1 |
||||||||||||||||||||||
|
1,0,1,0 |
|||||||||||||||||||||||
|
0,1,1,0 |
1,0,1,1 |
||||||||||||||||||||||
|
0,1,1,1 |
|||||||||||||||||||||||
|
0,0,1,0 |
0,0,1,1 |
1,1,0,0 |
1,1,0,1 |
||||||||||||||||||||
|
1,0,0,0 |
|||||||||||||||||||||||
|
0,1,0,0 |
1,0,0,1 |
||||||||||||||||||||||
|
0,1,0,1 |
|||||||||||||||||||||||
|
0,0,0,0 |
E24 |
||||||||||||||||||||||
|
0,0,0,1 |
|||||||||||||||||||||||
|
Рис. 1.1 |
|||||||||||||||||||||||
|
Определение. Пусть σi |
, σi |
2 |
, K, σi |
− фиксированная система чисел |
|||||||||||||||||||
|
1 |
k |
из 0 и 1 (1 ≤ i1 < i2 <K< ik ≤ n ). Множество всех вершин (α1 , K, αn )
куба Bn таких, что
αi1 =σi1 , αi2 =σi2 , K, αik =σik ,
называется (n − k) —мерной гранью.
Замечание. (n − k) -мерная грань является (n − k) -мерным подкубом
|
куба Bn . |
~ |
~ |
||||||||||||
|
Определение. Расстоянием (Хемминга) между вершинами α и β |
||||||||||||||
|
n |
~ |
~ |
n |
|||||||||||
|
куба B |
называется число ρ |
= ∑|αi − βi | (т.е. число |
||||||||||||
|
(α |
, β ) |
|||||||||||||
|
~ |
~ |
i=1 |
||||||||||||
|
отличаются друг от друга). |
||||||||||||||
|
координат, в которых наборы α |
и β |
|||||||||||||
|
~ |
~ |
куба B |
n |
– соседние, если |
||||||||||
|
Определение. Вершины α и |
β |
|||||||||||||
|
ρ |
~ |
~ |
~ |
~ |
||||||||||
|
(α, |
β ) |
=1, и противоположные; если ρ(α, β ) = n . |
||||||||||||
|
~ |
~ |
|||||||||||||
|
Определение. Говорят, что набор α предшествует набору β |
||||||||||||||
|
~ |
~ |
≤ βi для всех i = |
~ |
~ |
||||||||||
|
(обозначают αp β ), если αi |
1, K, n . Если αp |
β и |
||||||||||||
|
~ |
~ |
~ |
~ |
и |
||||||||||
|
α |
≠ β , то говорят, что набор α |
строго предшествует набору β |
||||||||||||
|
~ |
~ |
~ |
~ |
|||||||||||
|
обозначают α p β . Наборы α и β называют сравнимыми, если либо |
||||||||||||||
|
~ |
~ |
~ |
~ |
|||||||||||
|
αp β |
либо β pα . |
|||||||||||||
|
~ n |
) = f (x1 , K, xn ) |
такая, что |
||||||||||||
|
Определение. Функция f (x |
||||||||||||||
|
f : E2n |
→ E2 называется булевой функцией (или функцией алгебры |
|||||||||||||
|
логики) от n переменных. |
Замечание. Булевы функции являются удобными для описания, анализа и синтеза переключательных схем, выходные сигналы которых характеризуются лишь двумя уровнями напряжения: высоким (1) и низким (0). Поэтому в практических приложениях их еще называют
переключательными.
|
Для задания булевой функции |
~ n |
) требуется указать ее значения на |
|||
|
f (x |
|||||
|
n |
. При |
n ≥1 |
~ n |
) можно задать |
|
|
каждом наборе E2 |
функцию f (x |
таблицей T f (табл. 1.1), называемой таблицей истинности функции,
в которой наборы ~ K выписываются в порядке
σ = (σ1 , , σn )
возрастания их номеров (сверху вниз).
Табл. 1.1.
|
x1 |
x2 |
K |
xn−1 |
xn |
~ n |
) |
|
f (x |
||||||
|
0 |
0 |
K |
0 |
0 |
f (0, 0, K, 0, 0) |
|
|
0 |
0 |
K |
1 |
1 |
f (0, 0, K, 0, 1) |
|
|
0 |
0 |
K |
1 |
0 |
f (0, 0, K, 1, 0) |
|
|
K |
K |
K |
K |
K |
K |
|
|
0 |
1 |
K |
1 |
1 |
f (0, 1, K, 1, 1) |
|
|
1 |
1 |
K |
1 |
1 |
f (1, 1, K, 1, 1) |
При стандартном расположении наборов (в соответствии с увеличением
их номера), функцию ~ n можно задавать вектором ее значений f (x )
|
~ 2n |
= (α0 , α1 ,K, α2n −1 ) |
~ |
|||||||
|
α f |
(или α f ), где координата αi равна |
||||||||
|
~ n |
) |
в i -ой строке таблицы ( i = 0,1, K, 2 |
n |
−1 ), |
|||||
|
значению функции f (x |
|||||||||
|
~ |
|||||||||
|
т.е. на наборе σi . При этом значение переменной xk i -ой строке |
|||||||||
|
~ |
|||||||||
|
таблицы есть компонента σ k набора σi , которая определяются как |
|||||||||
|
~ |
|||||||||
|
соответствующая k -я цифра в записи числа i =ν(σ ) . |
|||||||||
|
Обозначим P2 (n) − множество всех булевых функций от n |
|||||||||
|
переменных, а P2 − множество всех булевых функций. |
|||||||||
|
Теорема. Число функций в P (n) равно 22 n . |
|||||||||
|
2 |
|||||||||
|
~ n |
) задается вектором |
||||||||
|
Доказательство. Поскольку функция f (x |
|||||||||
|
~ |
, α2n −1 ) , где αi |
{0,1} , 0 ≤ i ≤ 2 |
n |
−1 , то |
|||||
|
значений α f = (α0 , α1 ,K |
различных булевых функций от n переменных столько же, сколько различных 2n -разрядных двоичных векторов, т.е. 22 n .
Фиктивные и существенные переменные
Для сравнения булевых функций от одного количества переменных вводятся следующие понятия.
Определение. Переменная xi для функции f (x1 , K, xn ) называется существенной ( f зависит от xi существенно), если существует такой набор (β1 , K, βi−1 , βi+1 ,K, βn ) , что
f(β1 , K, βi−1 , 0, βi+1 ,K, βn ) ≠ f (β1 , K, βi−1 ,1, βi+1 ,K, βn ) .
Впротивном случае переменная xi – фиктивная, т.е. функция f не
зависит от xi .
Процедура удаления (введения) фиктивных переменных
|
Пусть переменная xi для функции |
~ n |
) – фиктивная. Тогда для ее |
||||||||||||||||||||||||
|
f (x |
||||||||||||||||||||||||||
|
удаления вычеркиваем все строки таблицы, в которых xi |
=1 и столбец |
|||||||||||||||||||||||||
|
переменной xi . В итоге получаем функцию от n −1 переменной. |
||||||||||||||||||||||||||
|
Определение. Две функции f1 и |
f2 от разного количества |
|||||||||||||||||||||||||
|
переменных равны, если одна получается из другой путем удаления или |
||||||||||||||||||||||||||
|
введения фиктивных переменных. |
||||||||||||||||||||||||||
|
~3 |
) задана таблицей 1.2. Определить фиктивные |
|||||||||||||||||||||||||
|
Пример. Функция f (x |
||||||||||||||||||||||||||
|
переменные функции. |
x3 функции |
|||||||||||||||||||||||||
|
Решение. Убеждаемся, сначала в том, что переменная |
||||||||||||||||||||||||||
|
~3 |
) |
является |
фиктивной. |
Удаляя |
ее, |
|||||||||||||||||||||
|
Табл. |
f (x |
|||||||||||||||||||||||||
|
1.2 |
~ 2 |
) |
||||||||||||||||||||||||
|
получим |
функцию |
(табл. |
1.3). |
|||||||||||||||||||||||
|
f (x |
||||||||||||||||||||||||||
|
Переменная |
x |
также является фиктивной. В |
||||||||||||||||||||||||
|
x1 |
x2 |
x3 |
~3 |
) |
||||||||||||||||||||||
|
f (x |
1 |
~ |
3 |
) = x2 (табл. 1.4). |
||||||||||||||||||||||
|
0 |
0 |
0 |
1 |
итоге получаем |
||||||||||||||||||||||
|
f (x |
||||||||||||||||||||||||||
|
0 |
0 |
1 |
1 |
Таблл.1.3 |
||||||||||||||||||||||
|
0 |
1 |
0 |
0 |
Табл. 1.4 |
||||||||||||||||||||||
|
x1 |
x2 |
~3 |
||||||||||||||||||||||||
|
0 |
1 |
1 |
0 |
f (x |
) |
|||||||||||||||||||||
|
x2 |
~ |
3 |
) |
|||||||||||||||||||||||
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
f (x |
|||||||||||||||||||
|
0 |
1 |
|||||||||||||||||||||||||
|
0 |
1 |
0 |
||||||||||||||||||||||||
|
1 |
0 |
1 |
1 |
|||||||||||||||||||||||
|
1 |
0 |
|||||||||||||||||||||||||
|
1 |
0 |
1 |
||||||||||||||||||||||||
|
1 |
1 |
0 |
0 |
|||||||||||||||||||||||
|
1 |
1 |
0 |
||||||||||||||||||||||||
|
1 |
1 |
1 |
0 |
Благодаря введенному понятию конечную совокупность булевых функций можно считать зависящей от одного и того же числа
переменных, являющегося объединением множеств переменных всех функций совокупности.
Функции от одной переменной
|
В таблице 1.5 представлены все булевы |
Табл. 1.5 |
|
|
функции одной переменной. |
||
Функции f0 и f3 называются
соответственно (тождественным) нулем и (тождественной) единицей.
Функция f1 называется
тождественной функцией и обозначается x .
Функция f2 называется отрицанием обозначается x или ¬x и читается «не x ».
|
x1 |
f0 |
f1 |
f2 |
f3 |
|
|
0 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
|
|
(или |
инверсией) x , |
Функции от двух переменных
В таблице 1.6 представлены все булевы функции от двух переменных.
Табл. 1.6
|
x1 |
x2 |
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Функция f1 называется конъюнкцией x1 и x2 , обозначается x1 & x2 или x1 x2 , или x1 x2 , и часто читается « x1 и x2 ».
Функция f6 называется суммой по модулю 2 x1 и x2 , обозначается x1 x2 или x1 + x2 , и часто читается « x1 плюс x2 ».
Функция f7 называется дизъюнкцией x1 и x2 , обозначается x1 x2 ,
|
и часто читается « x1 или x2 ». |
||
|
Функция f8 называется стрелкой Пирса x1 и |
x2 , |
обозначается |
|
x1 ↓ x2 , и часто читается «ни x1 , ни x2 » или «ни |
x1 |
и ни x2 ». В |
технической литературе ее обычно называют антидизъюнкцией или
функцией Вебба (а также функцией Даггера).
Функция f9 называется эквиваленцией (или эквивалентностью) x1 и x2 , обозначается x1 ~ x2 или x1 ≡ x2 , или x1 ↔ x2 , и читается « x1 эквивалентно x2 ».
|
Функция |
f13 |
называется импликацией |
x1 и x2 , |
обозначается |
|
|
x1 → x2 или x1 x2 , и часто читается « x1 имплицирует x2 |
» или «из |
||||
|
x1 следует x2 ». |
|||||
|
Функция |
f14 |
называется штрихом |
Шеффера |
x1 |
и x2 , |
|
обозначается x1 | |
x2 |
и часто читается «не x1 или не x2 » или « x1 и x2 |
не совместны». В технической литературе ее обычно называют
антиконъюнкцией.
Символы из множества B = {¬, &, , , ~, →, ↓, |} , в алгебре
логики участвующие в обозначениях элементарных функций, называют
логическими связками.
Задачи для самостоятельного решения
1. Найти номера следующих двоичных наборов:
а) (1010); б) (1001001); в) (0011001110); г) (10 K01), k ≥1 ;
123
|
k раз |
||
|
д) (1K10 K0), m, k ≥1 |
; е) (10 K01K10 K01), k ≥1 . |
|
|
{ 123 |
123 |
{123 |
|
m раз k раз |
k раз |
k раз k раз |
|
2. |
Найти двоичный набор длины k , являющийся разложением числа n : |
|
а) k = 6, n = 54 ; б) k =11, n = 2000 ; |
|
|
в) k = m +1, n = 2m +1 ; (m ≥1) ; г) k = m, n = 3 2m−2 −1 (m ≥ 2) . |
|
|
3. |
Для сравнимых наборов множества A из Bn выписать их в порядке |
предшествования ( p ). Выяснить, имеются ли в множестве A соседние
и противоположные наборы, и, если они имеются, выписать их:
а) A = {(001), (010), (101), (100), (110), (111)};
б) A = {(00111), (01011), (00110), (10110), (11010), (01010), (11100), (11011)}.
4. Найти:
|
~ n |
из B |
n |
, имеющих вес k ( n ≥ k ≥ 0, n ≥1 ); |
|||||||||||
|
а) число наборов α |
||||||||||||||
|
~ n |
из B |
n |
, удовлетворяющих условию |
|||||||||||
|
б) число наборов α |
||||||||||||||
|
2 |
n−1 |
~ n |
) < 2 |
n |
( n ≥1 ); |
|||||||||
|
≤ν(α |
||||||||||||||
|
в) число упорядоченных пар соседних наборов в B n ( n ≥1 ); |
||||||||||||||
|
~ n |
~ n |
) наборов из B |
n |
, таких, что |
||||||||||
|
г) число упорядоченных пар (α |
, β |
|||||||||||||
|
~ n |
~ n |
) = k ( n |
≥ k ≥1 ); |
|||||||||||
|
ρ(α |
, β |
|||||||||||||
|
~ n |
из B |
n |
веса k , у которых между любыми |
|||||||||||
|
д) число наборов α |
единичными компонентами находится не менее r нулевых компонент
( n − 2 ≥ r ≥ 0, n ≥ k ≥ 2 ). 5. Показать, что:
а) два различных набора в Bn , имеющих одинаковый нес, несравнимы; б) в Bn существуют только два сравнимых противоположных набора;
в) всякое подмножество наборов в B n , содержащее не менее n + 2 наборов, содержит пару несравнимых наборов ( n ≥ 2 );
|
г) число наборов в B |
n |
~ n |
, |
|||||||
|
, не сравнимых с фиксированным набором α |
||||||||||
|
имеющим вес k , равно 2n − 2n−k − 2k +1 ( n ≥ k ≥ 0, n ≥1 ). |
||||||||||
|
6. Найти число функций в P2 (n) , удовлетворяющих условиям: |
||||||||||
|
а) на данных k |
наборах значения функции фиксированы, а на |
|||||||||
|
остальных произвольные ( 2n−1 ≥ k ≥1, n ≥1 ); |
||||||||||
|
~ n |
из B |
n |
, удовлетворяющих условию |
|||||||
|
б) число наборов α |
||||||||||
|
2 |
n−1 |
~ n |
) ≤ 2 |
n |
( n ≥1 ); |
|||||
|
≤ν(α |
||||||||||
|
в) число упорядоченных пар соседних наборов в B n ( n ≥1 ). |
||||||||||
|
7. Найти число функций в P2 (n) , удовлетворяющих условию: |
||||||||||
|
а) на данных k |
наборах значения функции фиксированы, а на |
остальных произвольные ( 2n −1 ≥ k ≥1, n ≥1);
б) на противоположных наборах функция принимает одинаковые значения ( n ≥1 );
в) на каждой паре соседних наборов функция принимает противоположные значения ( n ≥1 );
г) функция равна 0 не менее чем на половине наборов ( n ≥1 ).
8. а) На аварийном пульте системы расположены четыре сигнальные лампочки L1 , L2 , L3 , L4 . Система выключается только в том случае, когда выполняется хотя бы одно из следующих условий: а) загорелась лампочка L1 , но не загорелась лампочка L2 ; б) загорелись лампочки
L2 и L3 , но не загорелась лампочка L4 ; в) загорелась лампочка L4 и
|
~ |
булевой |
||
|
не горит лампочка L1 . Построить вектор значений α f |
|||
|
~ 4 |
) , характеризующей условия выключения системы, т.е. |
||
|
функции f (x |
|||
|
~ 4 |
) =1 тогда и только тогда, когда справедливо хотя бы одно из |
||
|
f (x |
условий а), б), в); при этом предполагается, что xi =1 , если лампочка Li горит, и xi = 0 , если лампочка Li не горит.
б) Четырем членам B1 , B2 , B3 , B4 некоторой комиссии
сформулированы следующие условия посещения заседаний (хотя бы одно из них они должны выполнить): а) в заседании не участвует ни
B1 , ни B2 , но должен быть B3 ; б) в заседании принимают участие B2 и B4 , но отсутствует B3 ; в) на заседании должны присутствовать B1 и B4 . Обязан ли присутствовать на заседании член B3 ; если в нем не участвует B2 ?
9. Указать все фиктивные переменные у функции f :
|
~3 |
) = (10101010) |
~ 4 |
) = (1011010110110101) ; |
|
а) f (x |
; б) f (x |
~ 4 =
в) f (x ) (0101111101011111) .
10. Через P2c (n) обозначим множество всех булевых функций , зависящих от переменных x1 , x2 , K, xn и притом от каждой из них существенным образом.
а) Выписать все функции множества P2c (2) .
|
б) Найти число элементов множества Pc (3) . |
|
|
2 |
|
|
в) Доказать, что число элементов множества |
Pc (n) равно |
|
2 |
|
|
n |
|
|
∑(−1)k Cnk 22n−k . |
|
|
k =0 |
|
|
Ответы |
1. а) 10; б) 73; в) 206; г) 2k +1 +1; д) 2m+k − 2k ; е)
23k +1 + 22k +1 − 2k +1 +1 . 2. а) (110110); б) (11111010000); в)
|
n = (10 K01) |
; г) при m ≥ 4 |
n = 2m−1 + 2m−2 −1 и n = (10 1K1 ) ; |
|
123 |
{ |
|
|
k−1 раз |
k −2 раз |
при m = 3 n = (101) ; при m = 2 n = (10) . 3. а) (001) p (101) p (111); (010) p (110)}; (101) p (111); соседние: (001) и (101), (010) и (110), (101) и (100), (101) и (111), (110) и (111); противоположные (001) и (110), (010) и (101); б) (00110) p (00111), (00110) p (10110),
(01010) p (01011) p (11011), (01010) p (11010) p (11011); шесть пар соседних наборов; противоположных наборов нет. 4. а) Cnk ; б) 2n−1 ;
в) n 2n−1 ; г) Cnk 2n . Указание. Любой набор, отстоящий от
|
~ n |
~ n |
|
фиксированного набора α |
на расстоянии k , получается из α |
подходящей заменой некоторых k компонент на противоположные. д)
C k− − . n r(k 1)
6. а) Cnk ; б) 2n−1 ; в) n 2n . 7. а) 22 n −k ; б) 22 n−1 ; в) 2;
|
2 n |
−1 |
1 |
2 n−1 |
~ |
||||||
|
г) |
2 |
+ |
C |
n |
. 8. а) α f |
= (0101011111110010) ; б) Нет. |
||||
|
2 |
2 |
|||||||||
Указание. Предполагая, что xi =1 , если член Bi присутствует на заседании, и xi = 0 , если отсутствует, условия задачи с помощью булевой функции можно представить в виде
Булевы Функции
- Основные понятия.
- Аналитическое представление булевых функций.
- Функционально полные системы будевых функций.
- Минимизация булевых функций.
- Метод Квайна.
- Метод Квайна — Мак-Класки.
- Метод Блейка — Порецкого.
- Метод диаграмм Вейча.
- Минимизация коньюнктивных нормальных форм.
- Метод Петрика.
- Минимизация частично определенных булевых функций.
- Минимизация систем булевых функций.
Основные понятия
«
Функция f, зависящая от n переменных x1, x2, …., xn, называется булевой, или переключательной, если функция f и любой из ее аргументов Xi, (i E 1..n) принимают значения только из множества {О, 1}. Аргументы булевой функции также называются булевыми.
Произвольная булева функция задается одним из трех способов:
матричным (табличным), геометрическим и аналитическим.При матричном способе булева функция f (х1, …,хn) задается таблицей истинности (табл. 1.1 и 1.2), в левой части которой представлены все возможные двоичные наборы длины n, а в правой указывается значение функции на этих наборах.
| Таблица 1.1 | Таблица 1.2 | ||
| х1х2х3 | Номер набора |
||
| 000 001 010 011 100 101 110 111 |
0 1 0 0 1 1 0 1 |
0 1 2 3 4 5 6 7 |
0 1 0 0 1 1 0 1 |
Под двоичным набором y = < y1, y2,…,yn> yi E {0, 1} понимается совокупность значений аргументов х1, х2, …, xn булевой функции f. Двоичный набор имеет длину n, если он представлен n цифрами из множества {0,1}. В табл. 1.1 передставлены все двоичные наборы длины 3.
Иногда двоичные наборы в таблице истинности булевой функции удобно представлять номерами наборов. Запишем аргументы х1, х2, …, xn в порядке возрастания их индексов. Тогда любой двоичный набор y = < y1, y2,…,yn> yi E {0, 1} можно рассматривать как целое двоичное число N:
N=y1*2n-1+y2*2n-2+…+yn
называемое номером набора y. Например, двоичные наборы 101 и 111 имеют номера 5 и 7 соответственно. Очевидно, любая булева функция может быть задана таблицей истинности, в которой двоичные наборы заменены своими номерами (табл. 1.2).
Булевы функции, зависящие от большого числа переменных, задавать таблицей истинности неудобно в силу ее громоздкости. Например, таблица истинности булевой функции 8 переменных будет содержать 28 = 256 строк. Поэтому для задания функций многих переменных удобно использовать модификацию таблицы истинности.
Рассмотрим способ построения такой таблицы истинности для функции n переменных. Множество из n переменных функции разбивается на два подмножества: х1, х2, …, хj-1 и хj, хj+1, …, хn. Переменными x1, x2, …, xn отмечают строки таблицы истинности, задавая в каждой строке значение соответствующего двоичного набора длины j-1. Переменными xj, xj+i, …, xn отмечают ее столбцы, задавая в каждом столбце значения соответствующего двоичного набора длины n-j+1. Значение функции записывается в клетке на пересечении соответствующей строки и столбца (табл. 1.3).
| Таблица 1.3 | ||||
| x1,x2,…xj-1 | xj, xj+1, …,xn | |||
| 00…0 | 0…1 | … | 11…1 | |
| 00…0 | … | |||
| 00…1 | … | |||
| … | … | … | … | … |
| 11…1 |
При геометрическом способе булева функция f (х1, …, хn) задается с помощью n-мерного куба. В геометрическом смысле каждый двоичный набор у = <y1, y2,…,yn> yi E {0,1} есть n-мерный вектор, определяющий точку n-мерпого пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представляется вершинами n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, булева функция, заданная табл. 1.1, геометрически представляется 3-мерным кубом (рис. 1).
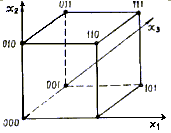
При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевых функций занимает особое место в проектировании цифровых автоматов. Фактически, все преобразования над булевыми функциями, необходимые для построения цифровых автоматов, ведутся на аналитическом уровне.
Рассмотрим области определения булевых функций. Как уже отмечалось, между двоичными наборами и двоичными числами существует взаимно однозначное соответствие. Следовательно, существует 2n различных наборов двоичных переменных.
Таким образом, областью определения булевой функции n переменных при матричном способе задания является множество всех возможных двоичных наборов длины n, а при геометрическом способе задания — множество всех вершин n-мерного единичного куба.
Булеву функцию, определенную на всех своих наборах, называют полностью определенной. В табл. 1.1, 1.2 приведены примеры полностью определенных булевых функций.
Булеву функцию n переменных называют неполностью определенной или частичной, если она определена не на всех двоичных наборах длины n. Неполностью определенная булева функция не попадает под определение, данное в начале , но при произвольном доопределении (на всех наборах, на которых она не определена) это несоответствие снимается.
Легко убедиться, что если булева функция f не определена на m наборах аргументов, то путем ее доопределения можно получить 2m различных полностью определенных функций. В табл. 1.5 приведен пример неполностью определенной булевой функции трех переменных.
| Таблица 1.5 | |
| х1х2х3 | F |
| 000 001 010 011 100 101 110 111 |
0 1 — 0 1 — 1 — |
Существует не более чем 22^n различных булевых функций n переменных. К этому выводу легко прийти, пользуясь простыми комбинаторными рассуждениями, и вспомнив, что на каждом из 2n наборов функции могут принимать два значения.
Функции двух переменных представлены в табл. 1.6.
Наиболее часто употребляются следующие:
| Таблица 1.6 | ||||||||||||||||
| х1х2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 00 01 10 11 |
0 0 0 0 |
0 0 0 1 |
0 0 1 0 |
0 0 1 1 |
0 1 0 0 |
0 1 0 1 |
0 1 1 0 |
0 1 1 1 |
1 0 0 0 |
1 0 0 1 |
1 0 1 0 |
1 0 1 1 |
1 1 0 0 |
1 1 0 1 |
1 1 1 0 |
1 1 1 1 |
f0 (x1, x2) = 0 — тождественный ноль (константа 0);
f1 (x1, x2) = x1 * x2 — конъюнкция. Вместо знака «*» иногда употребляется знак & или /. Эту функцию часто называют логическим произведением или логическим умножением;
f3 (x1, х2) = x1 — повторение x1;
f5 (x1, x2) = x2 — повторение х2;
f6 (x1, x2) = х1 x2 — сложение по модулю 2 или сумма mod 2 (далее +);
f7 (х1, х2) = x1 V x2 — дизъюнкция (логическое ИЛИ);
f8 (x1, x2) = x1 | х2 — функция Вебба (стрелка Пирса);
f9 (х1, х2) = x1 ~ x2 — эквивалентность;
f13(x1, x2) = x1 —> x2 — импликация;
f14(x1, x2) = x1x2 — штрих Шеффера;
f15(x1, x2) = 1-тождественная единица (константа 1).
Рассмотренные простейшие булевы функции позволяют строить новые булевы функции с помощью обобщенной операции, называемой операцией суперпозиции. Фактически операция суперпозиции заключается в подстановке вместо аргументов других булевых функций (в частности аргументов). Например, из функции f1 (x1, x2) с помощью подстановки f3 (х4, x8), f2 = x3 вместо аргументов х1 и х2 соответственно получаем функцию f1 (f3 (x4, x8), x3). Последняя от переменных х1, и х2 уже не зависит.
Отметим, что реально элементарной функции соответствует реализующий ее элемент, а суперпозиции булевых функций соответ-ствует соединение элементов

Операция суперпозиции позволяет увидеть качественный переход от n = 1 к n = 2. Действительно, суперпозиция функций одного аргумента порождает функции одного аргумента. Суперпозиция функций двух аргументов дает возможность строить функции любого числа аргументов (в приведенном примере построена функция трех переменных).
Суперпозиция булевых функций представляется в виде логических формул. Однако следует отметить:
- одна и та же функция может быть представлена разными формулами;
- каждой формуле соответствует своя суперпозиция и, следова-тельно, своя схема соединений элементов;
- между формулами представления булевых функций и схемами, их реализующими, существует взаимооднозначное соответствие.
Очевидно, среди схем, реализующих данную функцию, есть наи-более простая. Поиск логической формулы, соответствующей этой схеме, представляет большой практический интерес, а преобразование формул булевых функций основано на использовании соотноше-ний булевой алгебры.
Для булевой алгебры определены одна одноместная (унарная) операция «отрицание», две двухместные (бинарные) операции конъюнкция и дизъюнкция (обозначаются «*» (прим. далее «*» упускается), «v» соответственно).
В этой алгебре справедливы три аксиомы:
- закон коммутативности — х v у = у V х, ху = ух;
- закон ассоциативности — (х v у) v z = х v(y v z), (х y) z = х(у z);
- закон дистрибутивности — х (у v x) = ху v хz, х v y * z = (х v y)(х v z).
Под бинарной операцией на множестве А, в общем случае пони-мают отображение декартового произведения множеств (A Х А) в множество А. Иными словами, результат применения бинарной операции к любой упорядоченной паре элементов из А есть также элемент из множества А.
Под унарной операцией на множестве А понимают выделение (фиксацию) какого-либо элемента множества А.
Преобразование формул булевых функций применением только аксиом булевой алгебры малоэффективно. Для упрощения формул используется целый ряд соотношений.
Теоремы де Моргана
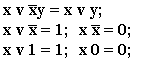
Алгебра Жегалкина
В ряде случаев, преобразования над формулами булевых функ-ций удобно призводить в алгебре Жегалкина.
Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение по модулю 2 (*, (прим. далее + ) ), а также константу 1. Здесь имеют место те же законы:
- х + y = y + х, х у = у х (закон коммутативности);
- х + (у + z) = (х + у) + z, х(у z) = (х у)z (закон ассоциативности);
- x (y + z) = x y + x z (закон дистрибутивности).
Для упрощения формул могут быть использованы следующие соотношения:
х + 0 = х;
х 1 = х;
х 0 = 0;
х + х = 0;
х х = х.
Из коммутативности и ассоциативности дизъюнкции следует, что дизъюнкция нескольких переменных может выполняться последовательно, причем порядок взятия дизъюнкции не влияет на результат.»
Использованная литература:
1) «Прикладная теория цифровых автоматов» Киев «Вища Школа» 1987
К.Г. Самофалов, А.М. Романкевич, В.Н. Валуйский,
Ю.С. Каневский, М.М. Пиневич
страницы (183 — 189).
Загрузка…
Номер набора при естественном упорядочении находится очень просто: через двоичную систему счисления.
Рассмотрим последний из наборов. Число $%1110001_2$% равно $%2^6+2^5+2^4+1=113$%. Поскольку нумерация идёт не с нуля, а с единицы, то надо прибавить единицу. Номер набора будет равен $%114$%.
Для вычисления номера относительно другого порядка, последовательно вычисляем номера наборов 1, 11, 111, 1110, и так далее (я рассматриваю тот же пример). Набор 1 имеет номер 2. Он чётный, поэтому из него формируются наборы 11, 10, где 1 и 0 идут в обратном порядке. При этом 10 получает номер 4, а 11 номер 3. Теперь он нечётный, и из него получаются 110 и 111 под номерами 5 и 6. Из 111 (номер чётный) формируются 1111 и 1110. Значит, 1110 получает номер 12.
По тому же принципу, следующие наборы получают вдвое большие номер после добавления очередного нуля, и 111000 имеет номер 48. Из него формируются 1110001 и 1110000 под номерами 95 и 96, то есть у нашего набора будет номер $%95$%.
Можно также указать более прямой способ перехода от набора в новой кодировке к набору в старой, что получается из правила, указанного по ссылке. Но это будет, наверное, уже излишняя информация.
табл. 1.3 и табл. 1.4). Пусть Й = й(Х1,, …, х,,), 22 = З(Х1,, …, х,) и (Х1, хг, … …, Хп) МНОжЕСтВО тЕХ ПЕРЕМЕННЫХ, КОТОРЫЕ ВСтРЕЧангтСЯ ХОТЯ бы в ОДНОЙ из формул Й и З, Т.е. (Х1, х2, . ° Хп) — 1хн .. ° Хм) ~-~ 0(Х1,, …, хд).
Формулы й и Ж называются эквивалентными (обозначение; й = З или й = 22), если на всяком наборе (О1, Ог, … …, О„) значений пероменных х1, хз, …, х„значения функций д2и и д1в, реализуемых соответственно формулами й и З, совпадают, т.е. ц1и(оп,…, о;„) = ~р~(О1,, …, Оз). Пусть Ф множество функциональных символов или логических связок, а Р множество соответствующих им функций.
Суперпозицией над,инооквством Р называется всякая функция Е, которую можно реализовать формулой над множеством Ф. Пусть й = й[~~»‘1,…, ~~»‘1) и 22 = З~д~п’1, …, д~»‘1). Говорят, что формулы й и З имеют одинаковое строение, если формула й может быть получена из формулы З путем замены каждого вхождения функционального символа д, * на символ (1 = 1, …, в).
Строение формулы отражает индуктивный процесс ее порождения в соответствии с определением формулы (см. определения 1 и 2). Строение формулы можно естественным образом характеризовать диаграммой (специальным графом, являющимся обычно ориентированным графом), вершинам которой приписаны функциональные символы (или логические связки) и символы переменных. Например, если формулы й у(21( (21( й~11( )) 121(( Й ) ф(01)) щ ~ (01 с — д~ 1(х, х), З вЂ” 1″1 1(1о~ ~1(АХ Ч у) 1В 2), у, й1 1(х Й 2)) рассматриваются над некоторым множеством Ф, содержащим логические связки Й, М, ~3 и функциональные символы ~~~1, д1~1, пр1, д11~1 и фу1щ1 (и, возможно, что-то еще), то их строение описывается диаграммами, изображенными на рис. 1.2. у д Функции алгебры логики.
Оиерацин суиериозиции 15 у<2) 12) А, Рис. 1.2 Если нужно обратить внимание именно на строение формулы 21 = = 2[11, …, Я, то используют запись Ж = С[21, …, Я. 2. Элементы булева куба. Первичные представления о булевых функциях. Пример 1. Найти номер двоичного набора зо раз т раз т раз Решение. Плина данного набора равна Зт+ 1, а его 1-я компонента равна 1 при 1 = 1, …, т, пз + 2, …, 2ьч + 1 и равна 0 в противном случае.
Следовательно, З З-1 зо 2т-~-1 ~, ‘ 2з з-1 — зо ~ 22 з-1 — 1+ ~~, 2з з-1 — 1 з=1 з.=1 У=за-~-2 22елз. 1 [2ззз 1) + 2ы [2ы 1) 2оз [22оз 1-1 2оз 1) Пример 2. Найти двоичный набор, являющийся разложением числа 325 (первая слева цифра в наборе должна быть равна 1). и Решение. Так как р(Н) = 2 оз 2″ ‘, то для нахождения ком- з=1 понент набора а, имеющего номер р(а), можно применить процедуру «последовательного деления с остатком на число 2»: а) ДЕЛИМ у[а) На 2, ОетатОК ЕетЬ аа, а ЧаСтНОЕ З11 = а1 2″ 2+… …
+ 11, — 2 2+ аи 1,. б) частное д1 делим на 2з остаток равен ао 1, частное 112 = = а1 2и + … + а„ з делим на 2, остаток равен а„ 2 и т.д. 16 Гл. 1. Способы задания и сводсзпва узуикиий алгебры логики до тех пор, пока на некотором ((и — 1)-м) шаге нс получим частное уи 1 — — о1 и остаток оз. В нашем случае р(Н) = 325. Используем описанную процедуру: 1) делим 325 на 2, находим частное 91 и остаток о„; 91 — — 162, ои = 1: 2) делим 162 на 2, частное равно 81, в остатке О, т. е, ои 1 — — О, 92 =81; 3) делим 81 на 2, за = 40, оо 2 = 1; 4)делим40на2, 94=20, ои з=О; 5) делим 20 на 2, 93 —— 10, ои 4 = 0; 6)делим10на2, с73=5, ои;=0; 7) делим 5 на 2, с12 = 2з ои — в 1; 
Следовательно, и = 9 и Н = (1з Оз 1, О, О, О, 1, О, 1). зз Замеч анно. Из формулы р(Н) = 2 оз 2″ ‘ видно, что для з=1 получения координаты о, набора Н можно поступать следующим образом: а) используя неравенство 2″ 1 < р(Н) < 2″,находим и; б) делим р(сз) на 2″ 141 и получаем остаток и, = о,.2″ ‘ + + о,41 . 2″ ‘ 1 +… + ои 1 2+ ои; в) делим р(Н) на 2″‘ 1 и получаем остаток г,.е1 = о,4.1 2″ ‘ 1 4-… ..,+пи 1 2+па; г) вычисляем разность т, — гзл 1 и делим ее на 2″ Полученное частное и есть значение координаты оо Например, если р(о) = 325 и нужно найти оз (см.
пример 2), то имеем; а)2и 1(325<2″,значит, п=9,таккак 2 =256<325<2 = 512; б) делим 325 на 23 за1 = 22 = 128, получаем остаток, равный 69; в) делим 325 на 2о 3 = 23 = 64 и получаем в остатке 5; г) гз — гз — — 64, и поэтому оз = 64/64 = 1. Пример 3. Найти двоичный набор длины т, являющийся разложением числа 2′» 1 — 2 (т ) 3). Решение. Представим число 2и’ 1 — 2 в виде суммы степеней двойки: 2т — 1 2 2с2из — 2 ц 212зи — 3+2т — 4+ +2+1) -2+2 — з+ +22+2 Значит, соответствующий числу 2 1 — 2 двоичный набор длины т таков: (01 … 10). ш — 2 раз Пример 4.
На множестве наборов и — 2 раз и — 3 раз и — 3 раз и — 3 раз и — 3 раз у 1. Функции алгебры логики. Операция еуперпозиции 17 где т! > 3, указать естественный частичный порядок 4 и выяснить, имеются ли в этом множестве соседние и противоположные наборы. Решение. Решая данную задачу, удобно просматривать наборы в порядке возрастания (или убывания) их весов, т.е.
начинать с наборов меньшего (или большего) веса и переходить последовательно к наборам с ббльшим (соответственно с меньшим) весом. Сначала рассмотрим случай п = 3. Множество А состоит из следующих наборов: (ООЦ, (100), (11Цз (01Ц, (000). Очевидно, что (000) 4 (ООЦ 4 (01Ц 4 (!1Ц н (000) 4 (100) 4 (11Ц. Соседними являются наборы (000) и (ООЦ, (000) и (100), (ООЦ и (01Ц, (01Ц н (111). Пары противоположных наборов таковы; (000) и (11Ц, (100) и (01Ц. Пусть теперь п = 4.
Тогда множество А выглядит так; ((ООП), (1010), (101Ц, (010Ц, (0010)). Имеем (0010) 4 (001Ц 4 (101Ц и (0010) 4 (1010); набор (010Ц не сравним ни с одним нз остальных наборов. Соседними являкется наборы (0010) и (001Ц, (0010) и (1010), (001Ц и (101Ц. Противоположных наборов только два: (010Ц и (1010). Предположим, что п > 5. Тогда А = ((00111… Ц з (1011… 10), (100…
01Ц, (0100… ОЦ з (0011… 10) ), ! раз ! раз 1 раз ! раз ! раз где 1 = и — 4 > 1. Обозначим эти наборы (в соответствии с порядком, в котором они выписаны выше) через Н!, ейз, аз, аа и ае. Возьмем набор а4 = (0100…0Ц (его вес равен 2) и посмотрим, сравним ли ! раз он с каким-либо другим набором. Так как у всех остальных наборов вторые компоненты нулевые, а веса не меньше 2, то они не могут быть сравнимы с набором а4. Затем переходим к набору аз сравниваем его с наборами Н„аз и аз. Нетрудно заметить, что начальные отрезки длины 3 наборов а! и аз, а также наборов аз и оз не сравнимы. Значит, набор аз не сравним ни с аз, ни с аз. Далее, рассматривая третьи и последние компоненты наборов аз и Йз, видим, что эти наборы тоже не сравнимы.
Берем теперь набор а! и сравниваем его с наборами аз и ае, Очевидно, что ае 4 аз, но а! и аз несравнимые наборы (достаточно обратить внимание на первые и последние компоненты этих двух наборов). Наконец, легко видеть, что Не 4 аз. Итак, имеем ое 4 а! и ае 4 аз. Соседними являются наборы а! и ае, а также аз и ае. Противоположных наборов два. оз и о4. Пример 5. Найти формулу для числа наборов аа из В», удовлетворяющих условию р(а «з 11а) = [(и+ Ц,!2[ и р(ех», уа) < [ге!!2[, где !1″ и 7″ фиксированные наборы и р()1″, ул) = [ге!!2[+ 1. Решение.
Не ограничивая общности рассуждений, можно считать, что Д» = 0″ и у» = (1 … 10…0). Пусть аа такой набор, ~ и / 2~ -!- ! раз что Р(етл,Оа) = [(и+ Ц/2[ и Р(Н»‘з У») < [в[2[. ПРедположим, что 2 Г.П. Гаврилов, А.А. Сапозкепко 18 Га, 1. Способы задавая и своде[пва д[упкиий аагебры логики сРсди псРвых его [пс[2) + 1 компонент Ровно 1 единичных [1 > 1). Тогда из остальных и — [пс[2] — 1 компонент единичными будут [[и+ 1) [[2) — 1 штук. Следовательно, при фиксированном о набор Нп сс [и/2) + 11 [с и, — [сс/2) — 1 1 можно выбрать [ . ) [ . [ способами, но при этом должновыполнятьсяусловие р[сг», 7″) = [в[[2) + 1 — в’+ [[и+ 1)1[2)— — 1 ( [гс/2), т.е.
2з > [[и+ 1)С2) + 1. Таким образом, искомое число наборов равно [[ [г[+ 1) [ — [ [2[ — ! ) Г».’1-‘»—.'(-«Г «1) В частности, при и = 1 имеем 2 (.) ( .) = 1 [если Д~ = О 1>о>1 1 — 1 то 7з = 1з и Нг = 7з), анри и = 2 получаем 2 (.) (1 .) = 2 сйг>з [если Дг = О, то 7~ = 1 и Нз = [01) и [10)).
Здесь полагаем, как обычно, (~) = 1. П р и м е р 6. Найти число функций, зависящих от перемен- ных ты ха, …, то, [т.е. принадлежащих множеству Рз[Х»)) и удов- летворяющих условию: функция Дт») равна О на каждом наборе Н», вес которого не превосходит сз[2, а на всех остальных наборах значе- ния функции произвольные [и > 1). Решение. Число наборов [из Вп), на которых значения функ- ции 1 зафиксированы, равно 2″ если и нечетное, [)(2″‘+ — [), На каждом из остальных наборов значение функции 7’ можно задавать произвольно [полагая его равным О или 1). Следовательно, число различных функций, удовлетворякгщих сформулированному вы— 1 2″ — з[ «.) ше условию, равно 2г при и нечетном и 2 ‘[» м) при п четном.