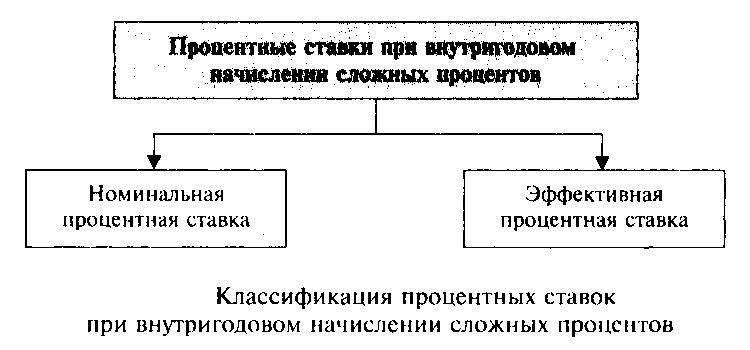
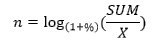Номинальная и эффективная ставка процентов
Краткая теория
В практике распространен вариант схемы
сложных процентов, когда капитализация вклада (начисление процентов) происходит несколько раз в году:
ежемесячно, поквартально, раз в полгода, а то и ежедневно. На практике очень
часто при этом в условиях сделки оговаривается не ставка процента за период
начисления, а годовая ставка процента j и период начисления, например, «20%
годовых с ежемесячным начислением процентов». Оговариваемая в контракте годовая
ставка процента j называется номинальной ставкой и служит для определения ставки
процента за период начисления. Пусть j − номинальная ставка, m − число
начислений в году, тогда ставка процента за период начисления находится по
простым процентам, и равна
.
За
лет будет
начислений,
поэтому наращенная сумма составит:
Процентные начисления за
лет
составят:
А процентные начисления за год:
Последняя формула – формула
действительной или эффективной ставки процента. Эта ставка измеряет тот
реальный относительный доход, который получают в целом за год от начисления
процентов, то есть служит мерой доходности сделки по схеме сложных процентов.
Эффективная ставка при
больше номинальной, в при
.
Замена в договоре номинальной ставки j при m-разовом
начислении процентов на эффективную ставку
не изменяет финансовых обязательств участвующих
сторон, то есть обе ставки являются эквивалентными ставками процента в финансовом отношении.
Финансовые
сделки различаются по длительности и по схемам расчета платежей:
простые процентные ставки
и
сложные процентные ставки,
простые и сложные учетные ставки, номинальные
процентные и учетные ставки и т. д. Чтобы иметь возможность сравнивать
эффективность сделок, осуществленных по разным схемам, используют эффективную
ставку процентов, дающую тоже соотношение между начальным капиталом
и конечным
, что и принятая схема. Если известны платежи по простой операции и срок
сделки, то находим выражение для определения эффективной ставки:
Кроме понятий номинальной и эффективной процентной ставки, в банковской учете используются понятия номинальная и эффективная учетная ставка.
Примеры решения задач
Задача 1
Сумма
размером
тысяч рублей инвестирована на
лет по ставке
годовых. Найдите наращенную за это время сумму
и ее приращение при начислении процентов:
а)
ежегодно;
б) по
полугодиям;
в)
ежеквартально;
г)
ежемесячно.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Наращенную сумму долга можно найти
по формуле:
-число
начисления процентов в году
-число полных
лет
а) при начислении процентов
ежегодно:
:
Приращение суммы составит:
б) при начислении процентов по
полугодиям:
Приращение суммы составит:
в) при начислении процентов
ежеквартально:
Приращение суммы составит:
г) при
начислении процентов ежемесячно:
Приращение суммы составит:
Ответ:
а)
;
б)
;
в)
;
г)
;
Задача 2
Определить
номинальную годовую процентную ставку, если эффективная ставка равна 28% и
сложные проценты начисляются ежеквартально
Решение
Эффективную
ставку можно найти из формулы:
Откуда
номинальная годовая ставка:
В
нашем случае
(ежеквартальное начисление процентов)
Получаем:
Ответ:
Задача 3
Вычислить эффективную ставку процента, если банк начисляет и
капитализирует проценты ежемесячно исходя из номинальной ставки 40% годовых.
Решение
Эффективную ставку процента
можно найти исходя из следующего равенства:
Откуда искомая эффективная
ставка:
В нашем случае:
–
банк начисляет проценты ежемесячно
Ответ:
Многие активы не учитывают в своей потенциальной доходности такой важный элемент, как сложный процент. Используя механизм капитализации, можно даже маленький капитал превратить в колоссальную сумму. Расскажем в статье, как работает сложный процент в инвестициях и в чем состоит его феномен.
Сложный процент — что это такое
Простыми словами, сложный процент – это процент, который начисляется на начальную сумму вложений и на проценты, накопленные за предыдущие периоды.
Основное преимущество инвестиций со сложным процентом состоит в том, что регулярное реинвестирование прибыли увеличивает доходность финансового актива и позволяет заработать еще больше в будущем.
Как работает и где используется
Механизм сложного процента действует по подобию снежного кома: инвестиции приносят доход, который в свою очередь также вкладывается и создает уже новый дополнительный доход. Чтобы получать эффект сложного процента от своих инвестиций, дополнительных стратегий или особых экономических знаний не требуется. Достаточно реинвестировать доходы, а не тратить их.
Сегодня капитализация процентов активно используется в банковской сфере и на рынке ценных бумаг (акции, облигации, ПИФы, ETF и т. д.). Также сложный процент можно применять и в недвижимости, когда доход от аренды направляется на покупку и сдачу в аренду новых недвижимых объектов.
Формула сложного процента
В интернете есть большое количество ресурсов, которые предлагают клиенту автоматически рассчитать капитализацию. Такие калькуляторы сложных процентов сильно экономят время. Однако если вы хотите досконально разобраться в работе капитализации процентов, лучше рассчитать ваши доходы от инвестиций вручную.
Итак, как капитализация процентов определяется по формуле?
Самая простая формула для расчета сложных процентов выглядит следующим образом:
FV = PV х (1+r/100)n , где
- FV – будущая сумма;
- PV – начальная сумма вложений;
- r – процентная ставка;
- n – количество лет (дней, месяцев и т. д.).
Главное качество, которое должны развить в себе все инвесторы, желающие применять силу сложных процентов, – это терпеливость. В первые годы реинвестирования капитала прибыль будет незначительной по сравнению с простым процентом, но на длительном промежутке времени доходность будет расти в геометрической прогрессии. Эффект сложных процентов позволяет доходу, который вы реинвестируете, приносить вам в будущем «проценты на проценты». Наиболее очевидный пример сложного процента – описание схемы работы банковского депозита.
Пример расчета
Допустим, клиент открыл банковский вклад на 100 000 рублей под 10% годовых.
Срок вложения – 5 лет. По договору также есть право каждый год снимать проценты со вклада. Сколько в итоге можно заработать?
Есть два подхода к формированию прибыли:
- Простая ставка процента. Каждый год инвестор будет снимать со счета все начисленные проценты и тратить их на свои нужды.
- Сложная ставка процента. Инвестор не снимает проценты. Начисленный доход реинвестируется и приносит еще больше прибыли.
Годовая доходность инвестора по вкладу в первый год составляет 10 000 рублей. Если регулярно снимать проценты, то за 5 лет клиент заработает 50 000 рублей чистой прибыли. Можно ли заработать больше? Можно. Если не снимать проценты, то доходность вклада с каждым годом будет увеличиваться, так как начисленные проценты будут реинвестироваться и генерировать новый доход. В таком случае через 5 лет инвестор заработает уже 61 051 рубль. Более наглядно математическую «магию» можно проследить в таблице ниже.
|
Годы |
Прибыль |
Разница | |
|
Простой процент |
Сложный процент | ||
|
1 |
10 000 р. |
10 000 р. |
0 р. |
|
2 |
20 000 р. |
21 000 р. |
+1000 р. |
|
3 |
30 000 р. |
33 100 р. |
+3100 р. |
|
4 |
40 000 р. |
46 410 р. |
+4610 р. |
|
5 |
50 000 р. |
61 051 р. |
+11 051 р. |
Через 5 лет разница в реальном выражении составит 11 051 рублей. Благодаря капитализации процентов инвестор сможет заработать не 50 000 рублей, а 61 051 рубль чистой прибыли. Данный пример показывает, что на длительной дистанции эффект сложного процента очевиден. Чем дольше реинвестировать, тем больше можно заработать.
Более упрощенно наши расчеты доходности можно было бы записать через ранее рассмотренную формулу сложного процента с капитализацией: FV = PV х (1+r/100)n
Нам известны следующие данные:
- PV = 100 000 рублей;
- r = 10%;
- n = 5 лет.
Подставим все значения в формулу расчета сложных процентов:
FV = 100 000 х (1+10/100)5 = 161 051 рубль
Как видно, результат тот же. Через 5 лет банковский вклад с капитализацией превратит 100 000 рублей клиента в 161 051 рубль.
Важно отметить, что многие банки практикуют политику ежемесячной капитализации, а не годовой. Это значит, что даже при номинальной годовой ставке в 10% (как в нашем примере) вкладчик, который не снимал деньги со счета все 12 месяцев, в конце первого финансового года получит уже не 10 000 рублей, а 10 446 рублей.
Примечание. Ежемесячная ставка составляет 1,0083%. (10% / 12 месяцев). В таком случае по формуле сложных процентов среднегодовая ставка с учетом капитализации составит уже 10,46%.
Сложный процент в инвестировании
Помимо банковской сферы, капитализация процентов активно используется и на фондовом рынке. Ведь реинвестирование прибыли – эффективный инструмент, который позволяет многим профессиональным участникам рынка добиваться значительных результатов даже без сложных финансовых стратегий и умных алгоритмов торговли. Рассмотрим, как работает сложный процент в разных инвестиционных активах.
Реинвестиции дивидендов по акциям
Заработать на акциях можно не только путем купли-продажи по более высокой цене, но и за счет получения дивидендов. При этом многие инвесторы придерживаются более долгосрочных взглядов и реинвестируют дивиденды, покупая новые акции. Как и при банковском вкладе, инвестор имеет возможность получить гораздо большую прибыль в будущем при условии, что курсовая стоимость новых акций будет расти, а не падать.
Среди российских компаний инвесторы чаще всего получают дивиденды от Газпрома, МТС и Лукойла.
Реинвестирование облигаций
Все владельцы облигаций (кроме дисконтных бумаг) получают от эмитента купонный доход. Он может выплачиваться компанией или государством один раз в месяц, квартал или даже год. Если инвестор не планирует тратить купонный доход, его также можно реинвестировать.
При этом важно понимать, что номинальная стоимость облигации обычно составляет 1000 рублей. Поэтому, если инвестор покупает долговую ценную бумагу, например, за 1100 рублей (рыночная цена), то выплата процентов и погашение основной суммы долга будет осуществляться из расчета именно в 1000 рублей. И в таком случае вкладчик будет нести убытки.
Чтобы реинвестирование купонных доходов приносило инвестору ощутимую прибыль, необходимо покупать бумаги по цене ниже номинальной стоимости, а не наоборот.
Вложения в ETF или ПИФ
Как правило, владельцы акций ETF или паев ПИФа не получают никаких дивидендов. Инвесторы зарабатывают только на купле-продаже ценных бумаг. Однако это не значит, что механизм реинвестирования в этих финансовых инструментах не работает. Дело в том, что структура активов ETF и ПИФов также состоит из акций и облигаций, по которым выплачивается периодический доход. Но чаще всего управляющие фондов сами автоматически реинвестируют дивиденды и купонные доходы без участия акционеров и пайщиков.
Таким образом, реинвестирование в ETF и ПИФах есть, но напрямую инвесторы на этот процесс повлиять практически не могут.
Банковский вклад с капитализацией
Банковские вклады с капитализацией – самый прибыльный вид депозитов. Каждое последующее начисление процентов всегда больше предыдущего, в результате чего общая доходность вклада также возрастает.
Чаще всего многие банки при рекламе вкладов с капитализацией пишут только номинальную ставку. Однако если вклад учитывает сложные проценты, то средняя процентная ставка будет немного выше.
Например, номинальная ставка при 5-летнем вкладе составляет 10%. А средний процентный доход с капитализацией уже будет исчисляться по ставке 12,21%. Это не означает, что каждый год клиент банка будет получать на 2,21% больше, чем написано в договоре. Просто реинвестирование процентов позволит в конце 5-летнего срока вклада заработать на 11,05% больше обычного (2,21% х 5 лет).
Благодаря сложным процентам прирост прибыли по вкладу со временем будет ускоряться, поскольку каждый раз банк начисляет проценты на всё более крупную сумму, а не на первоначальные вложения.
Делаем выводы
Главная цель всех инвесторов – получать максимальный доход от своих инвестиций. Добиться этого можно по-разному. Но самый простой способ – реинвестировать свои доходы. Механизм сложного процента позволяет инвестору зарабатывать на дистанции гораздо больше при прочих равных условиях. Повторно вкладывать капитал можно во что угодно. Например, покупать новые акции, облигации, паи ПИФов, акции ETF или даже просто открывать банковский вклад. Такой подход позволит увеличить капитал в долгосрочной перспективе и быстрее достичь финансовых целей.
Процесс реинвестирования не всегда приносит только прибыль. Чтобы не получать убытки от своих вложений, важно ответственно подходить к выбору активов и соотносить уровень риска с потенциальной доходностью.
Только при разумном инвестировании доход, полученный от первоначального капитала, способен генерировать новые денежные потоки и увеличивать совокупную доходность инвестиционного портфеля. В противном случае инвестора будет ожидать не рост капитала, а его падение.
Популярные вопросы
В чем разница между простыми и сложными процентами?
Простые проценты начисляются исключительно на начальную сумму вложений и не изменяют размер доходности инвестора со временем. Сложные учитывают ранее начисленные проценты и увеличивают общую прибыль вкладчика в долгосрочной перспективе.
Что сказал Эйнштейн про сложный процент?
Цитата Альберта Эйнштейна: «Сложные проценты – восьмое чудо света. Тот, кто понимает это, зарабатывает; тот, кто не понимает, платит».
Что такое сложные проценты по кредиту?
Сложные проценты по кредиту банк начисляет на оставшуюся сумму кредитного долга и на сумму ранее неуплаченных процентов по займу.
-
Наращение по сложным процентам
В средне и
долгосрочных операциях, если проценты
не выплачиваются сразу после их
начисления, а присоединяются к сумме
долга, то для наращения используются
сложные проценты.
Сложные проценты
отличаются от простых процентов базой
начисления. Если в простых процентах
она остается постоянной на весь срок
начисления, то в сложных при каждом
начислении процентные деньги присоединяются
к первоначальной базе. Говорят,
идет капитализация процентов.
Формула наращения
по сложным процентам, если проценты
начисляются один раз в году, имеет вид
,
где i — годовая (номинальная) процентная
ставка, n — число лет начисления,
— множитель наращения
по сложным процентам.
Задача
1.
Сумма, равная 800
тыс. руб., инвестируется на 3 года под
80% годовых. Найти наращенную сумму и
сумму процентов за этот срок, используя
простые и сложные проценты.
Решение:
1.Сложные проценты:
2. Простые проценты:
За
3 года 800 тыс. руб. увеличились в 5,832 раза
по сложным процентам и только в 3,4 раза
по простым процентам.
Задача
2.
Сумма, равная 800
тыс. руб., инвестируется на 3 месяца под
80% годовых. Найти наращенную сумму и
сумму процентов за этот срок, используя
простые и сложные проценты.
Решение:
1.Сложные проценты:
2. Простые проценты:
Итак, сложные
проценты работают лучше, если срок n
больше 1 года и простые проценты лучше
работают (дают большее наращение) внутри
года. Если срок начисления процентов 1
год, простые и сложные проценты дают
одинаковый результат.
Задача 3.
Найти сумму долга в 15 млн. руб. через 8
месяцев, 320 дней, 2 года, 10 лет по сложным
годовым ставкам 5% и 8%.
Решение:
.
;
.
Сумма долга зависит
от процентной ставки и числа лет
начисления. Сравните суммы по годам и
по процентным ставкам. (Сумма долга
растет с увеличением и процентной
ставки, и числа лет начисления).
-
Наращение процентов m раз в году. Номинальная ставка
Номинальная
ставка — годовая ставка, по которой
проценты начисляются m
раз в году. Обозначим эту ставку через
j.
Если проценты
начисляются m раз в году, то наращение
процентов происходит по ставке
,
общее число начислений процентов за
срок n равно mn.
Формула наращения
процентов по номинальной ставке j
при m-разовом начислении
процентов в году примет вид:
.
Если j —
номинальная ставка сложных процентов,
то
при m = 2 получается
полугодовая ставка,
при m = 4 — квартальная,
при m = 12 — ежемесячная,
при m = 365 (360) —
ежедневная ставка процентов.
Задача 4.
Очень важная задача! Обязательная
задача при зачете по сложным процентам.
Вложены деньги в
банк в сумме 5 млн. руб. на 2 года с
полугодовым начислением процентов под
20% годовых.
Составить схему
наращения капитала, найти наращенные
суммы по периодам начисления и к концу
срока двумя способами:
-
по определению
сложных процентов (как процент на
процент); -
по формуле
Решение:
Рассчитаем
полугодовую ставку
;
Множитель наращения
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сложная процентная ставка – ставка, которая в каждом новом периоде начисляется на сумму принципала и процентов за предыдущий период. Как правило, сложная процентная ставка применяется к ссудам, длительность которых составляет более одного года.
Как рассчитывается сложная процентная ставка?
Сложная ставка призвана мотивировать вкладчиков банка не снимать деньги как можно дольше. Формула для вычисления наращенной суммы выглядит следующим образом:
S = P * (1 + Ic) ^ n
Уточним, какие показатели обозначаются переменными: P – начальная сумма вклада, Ic – это ежегодная ставка, выраженная десятичной дробью (1 / c), n – число периодов (обычно лет). Весь множитель (1 + Ic) ^ n носит название множитель наращения. Его можно вычислить с использованием инженерного калькулятора.
Рассмотрим, как использовать формулу сложного процента, на примере:
Инвестор Z положил на депозит в банке 100 тыс. рублей (P) под сложный процент, равный 20% (с) на пять лет (n). Следует посчитать, сколько денег сможет снять с депозита инвестор Z через пять лет.
Подставив данные в формулу, мы получим:
S = 100000 * (1 + 0.2) ^ 5 = 248832 рубля
Чтобы уточнить, насколько достоверным оказался результат расчета, посчитаем сумму более детально – через таблицу:
|
Начальная сумма |
Начисленные проценты |
Конечная сумма |
|
|
1 год |
100000 |
20000 |
120000 |
|
2 год |
120000 |
24000 |
144000 |
|
3 год |
144000 |
28800 |
172800 |
|
4 год |
172800 |
34560 |
207360 |
|
5 год |
207360 |
41472 |
248832 |
Итог оказался совершенно точен. Если бы инвестор Z положил бы деньги под простую ставку, он получил бы почти на 50 тыс. рублей меньше (ровно 200 тыс. рублей). Отличием сложной ставки от простой является то, что суммы начисленных процентов меняются от периода к периоду: если за первый период инвестор Z получил процентами всего 20 тыс. рублей, то за пятый – уже 41 тыс. 472 рубля. Если бы инвестор оставил лежать деньги на счету и дальше, проценты копились бы по принципу «снежного кома». При простой процентной ставке такого интенсивного накопления не происходило бы – инвестор получал бы от периода к периоду по 20 тыс. рублей.
Виды сложных процентных ставок
Сложные ставки классифицируются на два вида:
Номинальная процентная ставка задается изначально и является базисом для вычисления эффективной процентной ставки, которая обозначается как Re. Применяется обратная формула:
1 + Re = FV / PV
где FV – это базисная сумма, а PV – наращенная.
Может применяться и другая:
Re = ((1 + r / m) ^ m) – 1
где R – номинальная ставка, а m – число внутригодовых выплат.
Стоит отметить две закономерности:
- Если m = 1, эффективная и номинальная ставки равны.
- Чем больше m, тем выше и эффективная ставка.
Полезные формулы
Существуют еще две формулы, которые необходимы инвестору для расчетов со сложными процентами:
- Ставка – под какой процент нужно внести деньги, чтобы получить желаемую сумму:
% = ((Сумма / X) ^ 1/n) – 1
- Срок – на сколько периодов следует положить деньги под процент, чтобы получить целевую сумму:
Просмотров 54.3к. Опубликовано 17.09.2018
Обновлено 01.03.2019
Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.
Формула сложного процента – это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).
Простой расчет сложных процентов
Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль – 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.
Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.
Этот эффект и получил название сложный процент.
Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.
Формула сложного процента:
SUM = X * (1 + %)n
где
SUM – конечная сумма;
X – начальная сумма;
% – процентная ставка, процентов годовых /100;
n – количество периодов, лет (месяцев, кварталов).
Расчет сложных процентов: Пример 1.
Вы положили 50 000 руб в банк под 10% годовых на 5 лет. Какая сумма будет у вас через 5 лет? Рассчитаем по формуле сложного процента:
SUM = 50000 * (1 + 10/100)5 = 80 525, 5 руб.
Сложный процент может использоваться, когда вы открываете срочный вклад в банке. По условиям банковского договора процент может начисляться например ежеквартально, либо ежемесячно.
Расчет сложных процентов: Пример 2.
Рассчитаем, какая будет конечная сумма, если вы положили 10 000 руб на 12 месяцев под 10% годовых с ежемесячным начислением процентов.
SUM = 10000 * (1+10/100/12)12 = 11047,13 руб.
Прибыль составила:
ПРИБЫЛЬ = 11047,13 – 10000 = 1047,13 руб
Доходность составила (в процентах годовых):
% = 1047,13 / 10000 = 10,47 %
То есть при ежемесячном начислении процентов доходность оказывается больше, чем при начислении процентов один раз за весь период.
Если вы не снимаете прибыль, тогда начинает работать сложный процент.
Формула сложного процента для банковских вкладов
На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:
% = p * d / y
где
p – процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;
d – период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;
y – количество дней в календарном году (365 или 366).
То есть можно рассчитывать процентную ставку для различных периодов вклада.
Формула сложного процента для банковских вкладов выглядит так:
SUM = X * (1 + p*d/y)n
При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.
Калькулятор сложных процентов для вклада
Расчет сложных процентов: Пример 3.
Рассмотрим 2 варианта:
1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете.
2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.
| Начальная сумма: 50 000 рублей | ||||
| Процентная ставка: 20% годовых | ||||
| Простой процент | Сложный процент | |||
| Сумма | Прибыль за год |
Сумма | Прибыль за год |
|
| Через 1 год | 60 000р. | 10 000р. | 60 000р. | 10 000р. |
| Через 2 года | 70 000р. | 10 000р. | 72 000р. | 12 000р. |
| Через 3 года | 80 000р. | 10 000р. | 86 400р. | 14 400р. |
| Через 4 года | 90 000р. | 10 000р. | 103 680р. | 17 280р. |
| Через 5 лет | 100 000р. | 10 000р. | 124 416р. | 20 736р. |
| Через 6 лет | 110 000р. | 10 000р. | 149 299р. | 24 883р. |
| Через 7 лет | 120 000р. | 10 000р. | 179 159р. | 29 860р. |
| Через 8 лет | 130 000р. | 10 000р. | 214 991р. | 35 832р. |
| Через 9 лет | 140 000р. | 10 000р. | 257 989р. | 42 998р. |
| Через 10 лет | 150 000р. | 10 000р. | 309 587р. | 51 598р. |
| Через 11 лет | 160 000р. | 10 000р. | 371 504р. | 61 917р. |
| Через 12 лет | 170 000р. | 10 000р. | 445 805р. | 74 301р. |
| Через 13 лет | 180 000р. | 10 000р. | 534 966р. | 89 161р. |
| Через 14 лет | 190 000р. | 10 000р. | 641 959р. | 106 993р. |
| Через 15 лет | 200 000р. | 10 000р. | 770 351р. | 128 392р. |
| Суммарная прибыль: | 150 000р. | 720 351р. |
Комментарии, как говорится, излишни. Вложения с использованием сложного процента НА ПОРЯДОК выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.
На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.
Как видите, на длительном промежутке времени очень важным становится то, под какой процент вы инвестируете деньги.
Через 15 лет при 10% годовых 50 тысяч рублей превратятся в 200 тысяч, при 15% – уже в 400 тысяч, а при 20% годовых – в 780 тысяч.
Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.
Вычисляем ставку и время
Из формулы расчёта сложного процента можно выразить процентную ставку и количество лет (месяцев).
Процентная ставка:
% = (SUM / X)1/n – 1
Расчет сложных процентов: Пример 4.
Какая процентная ставка должна быть, чтобы за 10 лет 50 000 рублей превратились в 100 000 рублей?
% = (100000 / 50000)1/10 – 1 = 0,0718 = 7,18 % годовых
Количество периодов (месяцев, лет):
n = log(1+%) (SUM / X)
Расчет сложных процентов: Пример 5.
Сколько потребуется лет, чтобы 50 000 руб. нарастились до 1 000 000 руб. при процентной ставке 40% ?
n = log(1+0,4) (1000000 / 50000) = 8,9 лет
Смотреть также:
- Сложные и простые проценты