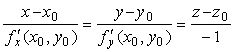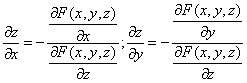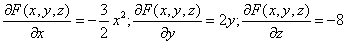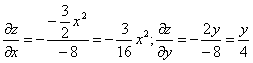Как найти нормаль цилиндра

Как я могу вычислить нормаль на поверхности цилиндра?

Я работаю над лучей, и я собрался добавить цилиндры на сцену. Точка, за которую я застреваю, — это найти нормальный вектор поверхности в точке, в которую попадает луч. Мне нужно это, чтобы иметь возможность делать рассеянное освещение. То, что у меня на данный момент, — это трехмерная точка, в которой луч камеры попадает в цилиндр и фактический цилиндр, который определяется точкой на центральной оси, вектор, представляющий направление оси и радиус. Итак, чтобы подытожить мой вопрос, как найти нормальный вектор в точке, имеющей точку попадания цилиндра, радиус, точку на ее оси и вектор направления оси?

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Поверхности

Простые поверхности.

Будем говорить, что функция (f(u, v)) непрерывно дифференцируема на замкнутом множестве (E subset boldsymbol^<2>), если она определена и имеет непрерывные частные производные (partial f/partial u) и (partial f/partial v) на открытом множестве (G), содержащем замкнутое множество (E).

Пусть (Omega) — ограниченная область в (boldsymbol^<2>), а функции (varphi(u, v)), (psi(u, v)) и (chi(u, v)) непрерывно дифференцируемы на замкнутом множестве (overline <Omega>= Omega cup partial Omega), где (partial Omega) — граница области (Omega). Тогда отображение (F: overline <Omega>rightarrow boldsymbol^<3>), определяемое формулами
$$
x = varphi(u, v),quad y = psi(u, v),quad z = chi(u, v),quad (u, v) in overline<Omega>,label
$$
называется непрерывно дифференцируемым.

Если при этом в каждой точке ((u, v) in Omega) ранг функциональной матрицы
$$
beginvarphi_(u, v)&psi_(u, v)&chi_(u, v)\varphi_(u, v)&psi_(u, v)&chi_(u, v)endlabel
$$
равен двум, то отображение (F: rightarrow boldsymbol^<3>) называется гладким.

Если (overline<Omega>) есть замкнутое ограниченное множество в (boldsymbol^<2>), a (F: overline <Omega>rightarrow boldsymbol^<3>) есть такое гладкое отображение, что соответствие между множествами (overline<Omega>) и (Sigma = F(overline<Omega>)) является взаимно однозначным, то будем множество (Sigma) называть простой поверхностью в (boldsymbol^<3>), а уравнения eqref будем называть параметрическими уравнениями простой поверхности (Sigma).

Пусть область (Omega) ограничена простым гладким или кусочно гладким контуром (gamma). Образ кривой (gamma) при гладком отображении (F: overline <Omega>rightarrow boldsymbol^<3>) будем называть краем простой поверхности (Sigma) и обозначать через (partial Sigma).

Если уравнение кривой (gamma) имеет вид
$$
u = u(t),quad v = v(t),quad alpha leq t leq beta,nonumber
$$
то уравнение (partialSigma) задается следующими формулами:
$$
x = varphi(u(t), v(t)),quad y = psi(u(t), v(t)),quad z = chi(u(t), v(t)),quad alpha leq t leq beta.label
$$

График функции (z = f(x, y)), непрерывно дифференцируемой на замкнутом ограниченном множестве (overline <Omega>subset boldsymbol^<2>), есть простая поверхность, определяемая параметрическими уравнениями
$$
x = u,quad y = v,quad z = f(u, v),quad (u, v) in overline<Omega>.label
$$

В этом случае матрица (beginx_&x_\x_&y_end) является единичной, а поэтому ранг матрицы eqref равен двум.

Например, график функции (z = x^ <2>+ y^<2>), ((x, y) in overline<Omega>), где (overline <Omega>= <(x, y): x^<2>+ y^ <2>leq 1>), есть простая поверхность. Окружность, получаемая при пересечении параболоида вращения (z = x^ <2>+ y^<2>) и плоскости (z = 1), является краем рассматриваемой простой поверхности.

Уравнения eqref простой поверхности можно записать и в векторной форме:
$$
boldsymbol = boldsymbol(u, v),quad (u, v) in overline<Omega>,quad boldsymbol(u, v) = varphi(u, v) boldsymbol + psi(u, v) boldsymbol + chi(u, v) boldsymbol.label
$$

С механической точки зрения формулы eqref определяют гладкую (без разрывов и изломов) деформацию плоской области (Omega) в множество (Sigma) (простую поверхность в пространстве (boldsymbol^<3>)). Для практических целей только простых поверхностей недостаточно. Например, сфера (x^ <2>+ y^ <2>+ z^ <2>= a^<2>) не является простой поверхностью в (boldsymbol^<3>). Интуитивно ясно, что сферу нельзя получить никакой гладкой деформацией плоской области.

Имея в виду приложения теории поверхностных интегралов, введем в рассмотрение класс почти простых поверхностей.

Пусть (Omega) — плоская область и (F: overline <Omega>rightarrow boldsymbol^<3>) — непрерывно дифференцируемое отображение. Будем множество (Sigma = F(overline<Omega>)) называть почти простой поверхностью в (boldsymbol^<3>), если найдется расширяющаяся последовательность ограниченных областей (<Omega_>) таких, что (overline<Omega>_ subset Omega_), (Omega = displaystylebigcup_^<infty>Omega_) и поверхности (Sigma_ = F(overline<Omega>_)) простые.

Сфера (S = <(x, y, z): x^<2>+ y^ <2>+ z^ <2>= a^<2>>) есть почти простая поверхность.

(vartriangle) Введем сферические координаты. Тогда сфера (S) есть образ прямоугольника (overline <Omega>= displaystyleleft<(varphi, psi): 0 leq varphi leq 2pi, -frac<pi> <2>leq psi leq frac<pi><2>right>) при непрерывно дифференцируемом отображении (F: overline <Omega>rightarrow S), определяемом формулами
$$
x = a cos varphi cos psi,qquad y = a sin varphi cos psi,qquad z = a sin psi.nonumber
$$

Образами отрезков (varphi = varphi_<0>), (displaystyle-frac<pi> <2>leq psi leq frac<pi><2>) являются меридианы, а при (displaystyle|psi_<0>| Рис. 52.1

Конус (K = <(x, y, z): x^<2>+ y^ <2>= z^<2>>) есть почти простая поверхность.

(vartriangle) Введем цилиндрические координаты. Тогда конус (K) есть образ полуполосы
$$
overline <Omega>= <(r, varphi): 0 leq r Рис. 52.2

Легко проверить, что (overline<Omega>_ subset Omega_), (Omega = displaystylebigcup_^<infty>Omega_) и что поверхности (Sigma_ = F(overline<Omega>_)) являются простыми. Поэтому конус (K) — почти простая поверхность. (blacktriangle)

Если (Sigma) есть простая поверхность, заданная векторным уравнением eqref, а непрерывно дифференцируемые функции
$$
u = u(u’, v’), v = v(u’, v’), (u’, v’) in Omega’nonumber
$$
задают взаимно однозначное отображение замыкания области (Omega’) на замыкание ограниченной области (Omega), причем якобиан отображения
$$
frac<partial(u, v)> <partial(u’, v’)>= begindisplaystylefrac<partial u><partial u’>&displaystylefrac<partial u><partial v’>\displaystylefrac<partial v><partial u’>&displaystylefrac<partial v><partial v’>endnonumber
$$
отличен от нуля в (overline<Omega>’), то уравнение
$$
boldsymbol = boldsymbol (u(u’, v’), v(u’, v’)) equiv boldsymbol<rho>(u’, v’);quad (u’, v’) in Omega’,label
$$
определяет ту же простую поверхность, что и уравнение eqref. Уравнения eqref и eqref называют различными параметризациями поверхности (Sigma).

Как и в случае кривых, можно расширить класс параметризаций, допуская и такие замены параметров, при которых непрерывная дифференцируемость, взаимная однозначность и необращение в нуль якобиана отображения нарушаются на границе области. Тогда можно получить такие параметризации простой поверхности, задаваемые функциями, непрерывная дифференцируемость которых не имеет места на границе области (Omega).

(vartriangle) Переход от уравнений eqref к уравнениям eqref задается формулами
$$
u = a cos varphi cos psi,quad v = a sin varphi cos psi,quad (varphi, psi) in Omega’.label
$$

Якобиан отображения eqref равен (a^ <2>sin varphi cos psi) и обращается в нуль при (psi = 0), то есть на части границы области (Omega’). Это приводит к тому, что при переходе к параметризации eqref частные производные функции (z = sqrt-u^<2>-v^<2>>) стремятся к бесконечности при приближении точки (u, v) к окружности (u^ <2>+ v^ <2>= a^<2>). (blacktriangle)

Как правило, в дальнейшем для простых поверхностей будут рассматриваться только такие параметризации, которые задаются непрерывно дифференцируемыми на замкнутом ограниченном множестве функциями.

Криволинейные координаты на поверхности.

Пусть простая поверхность (Sigma) задана векторным уравнением eqref. Предположим, что область (Omega) выпукла, ([a, b]) есть проекция области (Omega) на ось (u). Если (u_ <0>= in (a, b)), то прямая (u = u_<0>) будет пересекаться с областью (Omega) по отрезку (u = u_<0>), (alpha leq v leq beta) (рис. 52.3). Образ этого отрезка при отображении eqref есть кривая
$$
boldsymbol = boldsymbol (u_<0>, v), alpha leq v leq beta,label
$$
лежащая на поверхности (Sigma). Будем называть ее координатной кривой (u = u_<0>). Придавая (u_<0>) все значения из отрезка ([a, b]), получим семейство координатных кривых (u = operatorname). Аналогично строится и семейство координатных кривых (v = operatorname).

Рис. 52.3

В силу взаимной однозначности отображения eqref каждая точка (A) поверхности (S) однозначно определяется как пересечение двух координатных кривых, (u = u_<0>) и (v = v_<0>). Пара чисел ((u_<0>, v_<0>)) называется криволинейными координатами точки (A) поверхности. Запись (A(u_<0>, v_<0>)) означает, что точка (A) поверхности (Sigma) задана криволинейными координатами ((u_<0>, v_<0>)).

Например, в сферических координатах часть сферы (x^ <2>+ y^ <2>+ z^ <2>= a^<2>), ограниченная двумя меридианами и двумя параллелями, задается в криволинейных координатах (varphi), (psi) следующим образом:
$$
varphi_ <1>leq varphi leq varphi_<2>,quad psi_ <1>leq psi leq psi_<2>.nonumber
$$

На сфере координатные кривые (varphi = operatorname) — меридианы, а координатные кривые (psi = operatorname) — параллели.

На прямом круговом цилиндре координатными линиями будут образующие цилиндра и окружности, получающиеся при пересечении цилиндра плоскостями, перпендикулярными образующей.

Вектор-функция (boldsymbol (u_<0>, v)) есть непрерывно дифференцируемая функция параметра (v), и, следовательно, координатная кривая (u = u_<0>), определяемая равенством eqref, является непрерывно дифференцируемой. Вектор (boldsymbol_ (u_<0>, v_<0>)) является касательным к этой кривой в точке (A(u_<0>, v_<0>)). Аналогично, вектор (boldsymbol_ (u_<0>, v_<0>)) касателен к координатной кривой (v = v_<0>) в точке (A(u_<0>, v_<0>)). Заметим, что векторы (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_ (u_<0>, v_<0>)) не могут обратиться в нуль, так как в этом случае ранг матрицы eqref будет меньше двух. Следовательно, для простой поверхности координатные кривые являются гладкими.

Если область (Omega) не является выпуклой, а точка ((u_<0>, v_<0>)) лежит внутри (Omega), то нужно взять выпуклую окрестность точки ((u_<0>, v_<0>)), лежащую внутри (Omega). Тогда образ этой выпуклой окрестности будет куском поверхности (Sigma) и координатные кривые можно строить на этом куске поверхности (локально).

Касательная плоскость и нормаль к поверхности.

Пусть (Sigma) есть простая поверхность, заданная уравнениями eqref или векторным уравнением eqref. Рассмотрим точку (A(u, v)) на поверхности (Sigma), где ((u, v)) — внутренняя точка области (Omega). Построим координатные линии (u = operatorname) и (v = operatorname), проходящие через точку (A(u, v)). Векторы (boldsymbol_ (u, v)) и (boldsymbol_ (u, v)) будут касательными к соответствующим координатным линиям.

В любой точке (A(u, v)) простой поверхности (Sigma) векторы (boldsymbol_ (u, v)) и (boldsymbol_(u, v)) неколлинеарны. Направление вектора (N = [boldsymbol_, boldsymbol_]) при изменении способа параметризации или не меняется, или изменяется на противоположное.

(circ) Рассмотрим вектор (N = [boldsymbol_, boldsymbol_]) во всех точках поверхности (Sigma). Тогда
$$
boldsymbol=beginy_&z_\y_&z_endboldsymbol + beginz_&x_\z_&x_endboldsymbol + beginx_&y_\x_&y_endboldsymbol.nonumber
$$
Если (boldsymbol = boldsymbol<0>), то все компоненты вектора (boldsymbol) равны нулю, и ранг матрицы eqref будет меньше двух, что невозможно для простой поверхности. Пусть поверхность (Sigma) параметризована двумя способами, eqref и eqref. Тогда, воспользовавшись правилом нахождения частных производных сложной функции и аддитивностью и кососимметричностью векторного произведения, получаем
$$
boldsymbol’ = [boldsymbol<rho>_, boldsymbol<rho>_] = [boldsymbol_ frac<partial u> <partial u’>+ boldsymbol_ frac<partial v><partial u’>, boldsymbol_ frac<partial u> <partial v’>+ boldsymbol_ frac<partial v><partial v’>] =\= [boldsymbol_, boldsymbol_] left(frac<partial u><partial u’>frac<partial v><partial u’>-frac<partial u><partial v’>frac<partial v><partial v’>right) = [boldsymbol_, boldsymbol_] frac<partial(u, v)><partial(u’, v’)>,nonumber
$$
то есть
$$
boldsymbol’ = boldsymbol frac<partial(u, v)><partial(u’, v’)>.label
$$
Так как якобиан (J = displaystylefrac<partial(u, v)><partial(u’, v’)>) не обращается в нуль в области (Omega’), то векторы (boldsymbol’) и (boldsymbol) коллинеарны. Эти векторы сонаправлены, если (J > 0), и противоположно направлены, если (J Лемма 2.

Вектор нормали к простой поверхности (Sigma) в точке (A(u_<0>, v_<0>)) ортогонален ко всем гладким кривым, лежащим на поверхности и проходящим через точку (A(u_<0>, v_<0>)).

(circ) В самом деле, такая кривая есть образ при отображении eqref некоторой гладкой кривой, лежащей в области (Omega) и задаваемой уравнениями (u = u(t)), (v = v(t)), (alpha leq t leq beta).

Уравнение кривой на поверхности тогда имеет вид
$$
boldsymbol = boldsymbol(u(t), v(t)), alpha leq t leq beta, u(t_<0>) = u_<0>, v(t_<0>) = v_<0>.
$$

Касательный вектор (boldsymbol<tau>) к этой кривой в точке (A) есть
$$
boldsymbol <tau>= frac

(boldsymbol(u(t_<0>, v(t_0))) = boldsymbol_(u_<0>, v_<0>) frac)>

+ boldsymbol_(u_<0>, v_<0>) frac)>

.nonumber
$$

Итак, (boldsymbol<tau>) есть линейная комбинация векторов (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_(u_<0>, v_<0>)). Так как вектор (boldsymbol) ортогонален (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_(u_<0>, v_<0>)), то он ортогонален и вектору (boldsymbol<tau>), то есть вектор нормали к поверхности в точке (A) ортогонален к любой гладкой кривой, лежащей на поверхности и проходящей через точку (A). (bullet)

Плоскость, проходящая через точку (A(u, v)) поверхности и ортогональная вектору (boldsymbol), называется касательной плоскостью к поверхности в точке (A). Пусть ((X, Y, Z)) — декартовы координаты точки касательной плоскости и пусть (boldsymbol = Xboldsymbol + Yboldsymbol + Zboldsymbol). Тогда векторы (boldsymbol-boldsymbol(u, v), boldsymbol_(u, v), boldsymbol_(u, v)) параллельны касательной плоскости, следовательно, их смешанное произведение равно нулю. Поэтому векторное уравнение касательной плоскости имеет вид
$$
(boldsymbol-boldsymbol(u, v), boldsymbol_(u, v), boldsymbol_(u, v)) = 0.nonumber
$$

В силу равенства eqref форма этого уравнения не зависит от выбора параметризации поверхности. Уравнение касательной плоскости в координатах имеет следующий вид:
$$
beginX-x(u, v)&Y-y(u, v)&Z-z(u, v)\x_(u, v)&y_(u, v)&z_(u, v)\x_(u, v)&y_(u, v)&z_(u, v)end = 0.nonumber
$$

Нормалью к поверхности в точке (A(u, v)) называется прямая, проходящая через точку (A) и параллельная вектору нормали в точке (A). Так как при изменении параметризации вектор нормали не меняет своего направления или изменяет его на противоположное в каждой точке поверхности, то нормаль не зависит от параметризации. Ее векторное уравнение имеет вид
$$
boldsymbol-boldsymbol(u, v) = k[boldsymbol_, boldsymbol_], -infty

Кусочно гладкие поверхности.

Из определения простой поверхности, данного в п. 1, следует, что она есть гладкий и взаимно однозначный образ некоторой плоской области, то есть получается из этой области при помощи гладких (без изломов) деформаций (отображений). Ясно, что многие объекты, которые мы привыкли называть поверхностями, не будут простыми поверхностями. Так, сфера не может быть непрерывным образом деформирована в плоскую область. Коническая поверхность не может быть получена гладкой деформацией плоской области.

Попытки дать общую классификацию поверхностей увели бы нас далеко в область высшей геометрии. Замечательным классом поверхностей в (boldsymbol^<3>) являются гладкие многообразия размерности 2, то есть связные множества, которые локально (в окрестности каждой своей точки) устроены, как простая гладкая поверхность. Например, сфера будет гладким многообразием. Если (A) есть точка сферы радиуса (a), то шар (S_<varepsilon>(A)) при (varepsilon Рис. 52.4

Из гладких кусков можно склеивать не только гладкие многообразия, но и связные поверхности, имеющие ребра и вершины (например, поверхности многогранников) (рис. 52.5).

Рис. 52.5

Мы не станем тут заниматься математической формализацией таких понятий, как разрезание и склеивание поверхностей, и тем более основанной на этом классификации поверхностей. Заметим только, что трудности возникают при построении общих теорий. В любом разумном частном случае нет проблем с разрезанием поверхности на простые куски. Поверхность, которую можно разрезать на конечное число простых кусков, будем называть кусочно гладкой.

Ориентируемые поверхности.

Будем говорить, что гладкая поверхность ориентируема, если можно построить на этой поверхности непрерывное поле единичных нормальных векторов. Говорят, что это поле единичных нормалей определяет ориентацию (или сторону) поверхности. Меняя направление всех единичных нормалей на противоположное, получим опять непрерывное поле единичных нормальных векторов. Говорят, что оно определяет противоположную ориентацию (другую сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов
$$
boldsymbol = frac<[boldsymbol_, boldsymbol_]><|[boldsymbol_, boldsymbol_]|>.label
$$

Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), так и неориентируемыми (односторонними).

Торы, изображенные на рис. 52.4, ориентируемы; бутылка Клейна — неориентируемая (односторонняя) поверхность. Легко построить лежащий на этой поверхности замкнутый гладкий контур такой, что, выбирая в какой-то точке контура вектор единичной нормали к поверхности и непрерывно изменяя его при движении по контуру, мы придем к начальной точке с противоположным направлением нормали. Следовательно, на бутылке Клейна построить непререрывное поле единичных нормальных векторов невозможно.

Заметим еще, что сфера, тор, тор с двумя дырами (рис. 52.4) делят пространство на ограниченную и неограниченную области, общей границей которых они являются. Бутылка Клейна таким свойством не обладает.

Можно доказать, что гладкая поверхность, являющаяся границей области в (boldsymbol^<3>), ориентируема. Ее внутренняя сторона задается нормальными векторами, направленными внутрь области (внутренними нормалями), внешняя сторона определяется внешними нормалями. Очевидно, что для построения поля внутренних нормалей к границе области достаточно построить внутреннюю нормаль к какой-то одной точке границы.

Рис. 52.6

Каждая плоскость делит пространство (boldsymbol^<3>) на два полупространства. Если плоскость рассматривать как границу полупространства, то внутренняя нормаль определяется естественным образом как направленная внутрь полупространства (рис. 52.6). Если (partial G) есть гладкая граница области (G), то касательная плоскость в точке (x in partial G) называется опорной, если область лежит по одну сторону от касательной плоскости, то есть в одном из полупространств, определяемых этой плоскостью. В точке (x in partial G) определена внутренняя нормаль (рис. 52.7).

Рис. 52.7

Границу области (G), ориентированную внешними нормалями, будем обозначать через (partial G), а внутренними — через (partial G^<->).

Несколько более сложно определяется ориентация кусочно гладких поверхностей.

Рис. 52.8

Пусть (Sigma) — простая поверхность (рис. 52.8), то есть гладкий и взаимно однозначный образ замыкания плоской области (Omega). В декартовых координатах отображение задается равенствами eqref. Прообразом гладкого простого контура (Gamma subset Sigma) будет простой гладкий контур (gamma subset Omega). Будем говорить, что контур (Gamma) ориентирован положительно, если его прообраз (gamma) ориентирован в плоскости ((u, v)) положительно (рис. 52.9), то есть при обходе контура (gamma) область, им ограничиваемая, остается слева (вектор касательной и вектор внутренней нормали образуют правую пару векторов в ориентированной плоскости ((u, v))). Будем говорить, что ориентация простой поверхности (Sigma), задаваемая полем единичных нормалей
$$
boldsymbol = frac<[boldsymbol_, boldsymbol_]><|[boldsymbol_, boldsymbol_]|>,nonumber
$$
согласована с положительной ориентацией простых контуров, лежащих на поверхности (Sigma).

Рис. 52.9

Покажем, что предложенное правило согласования ориентации поверхности с ориентациями простых контуров, лежащих на поверхности, совпадает с известным правилом правого винта. Пусть (A(u_<0>, v_<0>) in Sigma), то есть ((u_<0>, v_<0>) in Omega). Без ограничения общности можно считать, что (u_ <0>= 0), (v_ <0>= 0). Построим в точке (A)(0,0) касательную плоскость и ориентируем ее вектором нормали (boldsymbol) или, что то же самое, парой векторов ((boldsymbol_)(0, 0), (boldsymbol_)(0,0)). Возьмем в плоскости переменных (u), (v) окружность радиуса (varepsilon) с центром в точке (0,0):
$$
u = varepsilon cos t, v = varepsilon sin t, 0 leq t leq 2pi.nonumber
$$

Ее образ на поверхности есть простой замкнутый контур (Gamma):
$$
boldsymbol = boldsymbol (varepsilon cos t, varepsilon sin t), 0 leq t leq 2pi.nonumber
$$

С точностью до (boldsymbol(varepsilon)) при (varepsilon rightarrow 0) получаем, что
$$
boldsymbol = boldsymbol(0,0) + varepsilon boldsymbol_(0,0)cos t + varepsilon boldsymbol_(0,0)sin t + boldsymbol(varepsilon).nonumber
$$

С точностью до (boldsymbol(varepsilon)) кривая (Gamma) есть эллипс в касательной плоскости, ориентированной парой векторов ((boldsymbol_)(0, 0), (boldsymbol_)(0,0)).

Ориентация эллипса положительна (рис. 52.10). Если смотреть на касательную плоскость со стороны вектора нормали (boldsymbol), то движение по эллипсу происходит против часовой стрелки, от вектора (boldsymbol_)(0, 0) к вектору (boldsymbol_)(0, 0) (область, ограничиваемая эллипсом, остается слева).

Рис. 52.10

Пусть кусочно гладкая поверхность (Sigma) склеена из гладких простых кусков (Sigma_<1>, Sigma_<2>, ldots, Sigma_). Если склеивание происходит вдоль кривой (gamma), то после удаления концов кривой (gamma) она входит в края двух и только двух поверхностей (Sigma_). Кусочно гладкая поверхность (Sigma) называется ориентируемой, если можно так ориентировать гладкие куски (Sigma_), (i = overline<1, n>) что после согласования ориентации (Sigma_) с ориентациями (partial Sigma_) любая кривая склейки будет входить в состав краев соответствующих двух поверхностей с противоположными ориентациями (рис. 52.11).

Рис. 52.11

Можно показать, что кусочно гладкая поверхность, являющаяся границей ограниченной области, ориентируема, при этом каждый ее гладкий кусок можно ориентировать внутренними нормалями. В дальнейшем мы будем рассматривать только ориентируемые гладкие и кусочно гладкие поверхности.

источники:

http://math.semestr.ru/math/tangent-plane.php

http://univerlib.com/mathematical_analysis/curve_surface_integrals/surfaces/

Здесь
мы будем использовать формулы
параметрического описания поверхности
цилиндра. В одной из возможных
разно­видностей такого описания
применяются следующие параметры —
долгота (l)
и
вы­сота (h).

где l
= 0…360°, h
=-0.5… 0.5. ВеличинамиR
и
Н
обозначим
соответст­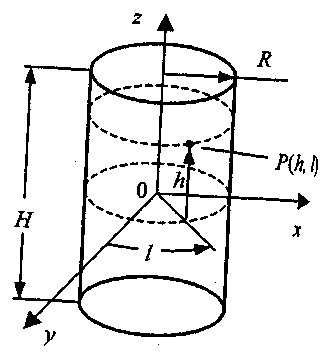венно радиус и общую высоту цилиндра
(рис. 5.28).

Рис.
5.28. Цилиндр

Каркасное
изображение

Построение
каркасного изображения полностью
аналогично рассмотренному выше способу
для шара. Для цилиндра также рисуются
меридианы (здесь это вертикальные линии)
и параллели (эллипсы). На рис. 5.29 изображен
каркас из прямых линий — ребер вписанного
многогранника.

Одним
из свойств каркасного изображения без
удале­ния невидимых точек является
иллюзия неопределен­ности ракурса.
Непонятно — это вид сверху или вид
снизу. Раньше вы, наверное, уже замечали
подобный эффект, например, когда мы
рассматривали каркасное изображение
шара.

Рис.
5.29. Каркас

Удаление
невидимых точек

На рис. 5.30 показано
изображение цилиндра в двух вариантах—
с верхней крышкой и без.

Рис.
5.30. Показ
с удалением невидимых точек

В обоих случаях
для создания иллюзии объемности здесь
выделены черным цветом видимые ребра
аппроксимирующего многогранника. Для
показа по­верхности многогранника с
крышкой достаточно показать ребра
граней пе­редней стороны и крышку.
Задние грани являются невидимыми (рис.
5.31).

Если верхняя крышка
отсутствует, то видимыми являются все
грани. В этом случае следует рисовать
объект, начиная с самых дальних граней
задней сто­роны.

Грани можно выводить
попарно, начиная с грани, соответствующей
самой дальней точки, как показано на
рис. 5.32.

Рис.
5.31. Расположение
задних граней. Рис.
5.32.
Порядок

вывода
граней

Долгота дальней
точки определяется расположением
камеры:

где [… ] — целая
часть

Такой
метод сортировки граней можно использо­вать
не только для цилиндра, но и для достаточно
широкого класса поверхностей. На рис.
5.33 пока­зан пример поверхности
вращения, изображенной описанным выше
методом. Такая поверхность по­добна
цилиндру. Единственное отличие здесь
со­стоит в том, что боковая поверхность
криволиней-_Рис
5
33
поверхность на по вертикали, поэтому
для аппроксимации че-
вращения

тырехугольными
гранями следует использовать

двойной
цикл — как по долготе (l),
так
и по высоте (h).
Подобные
пример мы рассмотрим несколько позже.

Освещенный
многогранник

Здесь мы будем
рассматривать изображение боковой
поверхности цилиндра, аппроксимированного
многогранником. Грани нужно изображать
цветом в соответствии с выбранной
моделью отражения. Мы будем рассматривать
ци­линдр без крышек. Это позволяет
наглядно проиллюстрировать проблемы
показа поверхностей, для которых могут
быть видимыми обе стороны.

В чем суть проблемы?
Проблема в выборе направления нормали
к грани. В предыдущем разделе мы
рассматривали шар, и вы, наверное,
заметили, что

итам
мы аппроксимировали поверхность
многогранником. Однако для шара указанной
проблемы не существует, у него всегда
видимой является внешняя сторона
поверхности. Необходимое направление
нормалей для всех граней легко обеспечить
соответствующей нумерацией вершин
каждой грани. Для цилиндра без крышек
нельзя жестко зафиксировать направление
векторов (нормали, если предполагается
показывать цилиндр с разных ракурсов
(на­пример, изменяя углы поворота
камеры а
и
β).

_;Для
диффузного отражения цвет грани
определяется значением косинуса уг­ла
между лучом источника света и нормалью
к поверхности. Одним из вари­антов
решения проблемы является взятие модуля
косинуса, если косинус от­рицательный.
Это можно делать, когда положение
источника света совпадает с положением
камеры. На рис. 5.34 показано несколько
вариантов задания направления нормалей.

Рис.
5.34. Варианты выбора направления нормалей

На рис. 5.35 изображена
боковая поверхность многогранников,
аппроксими­рующих цилиндр с различной
точностью. Моделируется боковое
расположе­ние источника света.

Рис.
5.35. Аппроксимация боковой поверхности
плоскими гранями

Гладкая
боковая поверхность

Рассмотрим
один из алгоритмов изображения гладкой
боковой поверхности цилиндра — рисо­вание
вертикальными линиями. На рис. 5.36
по­казаны: вид сверху (ось z
мировых
координат направлена на нас), полутоновое
изображение поверхности в аксонометрической
проекции и направление осей мировых
координат (х,
у, z).
Положение
камеры здесь задано одним углом β
Источник света располагается так же,
как и ка­мера. В этом случае цвет
пикселов вертикали бо­ковой поверхности
определяется коэффициентом отражения

где R
—
радиусцилиндра.
Вдоль любой вертика­ли боковой поверхности цвет пикселов
здесь _ _ „_ „

_т.

Рис.
5.36. Рисование

одинаков. Кроме
того, при данном расположении
вертикальными линиями источника света
имеет место полная симметрия относительно
центральной вертикали. Это позво­ляет
построить достаточно быстрый алгоритм
рисования. Крышки цилиндр можно также
рисовать вертикалями, но это уже не
принципиально.

h
= Н sin
p

Определяем
цвет крышки (clrO)
по
значению cos
P
for
(х
= 0; x<=R;
x++)
{

у
=
корень квадратный из ( R²
— х²
) к = у
/
R

Определяем
цвет боковой поверхности (clr)
в
зависимости от к

у
ж
у
COS
P

Рисование
двух симметричных вертикалей боковой
поверхности:

вертикаль
от (хс+х,
ус+у — h/2)
до
(хс+х,
ус+у
+ h/2)
цветом
clr

вертикаль
от (хс-х,
ус+у — h/2)
до
(хс-х,
ус+у
+ h/2)
цветом
clr

Рисование
двух вертикалей крышки:

вертикаль
от (хс+х,
ус-у — h/2)
до
(хс+х,
ус+у
—
h/2)
цветом
clrO

вертикаль
от (хс-х,
ус-у —
h/2)
до
(хс-х,
ус+у
—
h/2)
цветом
clrO

>

Здесь
(хс,
ус) —
экранные координаты центра цилиндра.

Входе
работы этого алгоритма вычисляются
координаты точек эллипса для одного
квадранта. Вначале определяется
координата у
для
круга, а затем она умножается на
коэффициент сжатия эллипса (cosβ).
Определение величины cosβ
целесообразно вынести за цикл — вычислить
ее один раз в начале ра­боты. В теле
цикла нужно вычислять квадратный корень
и выполнять не­сколько операций
умножения и деления. Хотя эти операции
являются мед­ленными, но они выполняются
сразу для нескольких пикселов,
расположен­ных по симметричным
вертикалям. Чем длиннее вертикали, тем
меньшую часть от общего времени вывода
составляют такие операции (поэтому не
обязательно для вычисления точек эллипса
использовать алгоритм Брезенхэма —
хотя почему бы и нет?). Поскольку собственно
вертикаль рисуется дос­таточно быстро,
то данный алгоритм может успешно
конкурировать по бы­стродействию с
алгоритмами полигонального вывода. Еще
одно полезное свойство — высокое
качество рисования гладкой боковой
поверхности. Не­достатком данного
алгоритма является показ только
вертикального располо­жения цилиндра,
в то время как полигональную форму можно
свободно по­ворачивать в пространстве.

Следует
учитывать, что данный алгоритм можно
использовать для углов на­клона камеры
β
от
0 до 90° (вид сверху). Этим и объясняется
рисование толь­ко верхней крышки. Для
вида снизу (β
от 90 до 180°) необходимо показы­вать
нижнюю крышку (верхнюю не нужно, она
становится невидимой). Алгоритм легко
обобщить.

Если
цилиндр является отдельным элементом
некоторой сложной сцены, то при выводе,
например, с использованием Z-буфера
необ­ходимо соответствующим образом
построить цикл вывода вертикалей.

Теперь
рассмотрим произвольное располо­жение
источника света. Как и прежде, будем
рассматривать только один точечный
источ­ник, расположенный в бесконечности.
Пусть расположение источника описывается
двумя углами наклона (а_с
и
β_с).
Положение каме­ры будем задавать
двумя углами наклона — (а
и
β).
Для
простоты вначале положим угол поворота
камеры а
=
0.

На
рис. 5.37 изображен цилиндр, освещенный

сбоку.
Здесь показана только боковая по-
_Рис.
₅.37.
Освещение слева

верхность — без
верхней и нижней крышек. Это более
сложный вариант по­каза, поскольку
нужно рисовать и внутреннюю часть
поверхности.

Рассмотрим
четыре точки, расположенные симметрично
на поверхности ци­линдра. Для первой
точки угол между нормалью к боковой
поверхности и лучом от источника света
составляет φ₁₌
φ
— а_с.
Для
второй точки анало­гичный угол равен
φ
₂
=
φ
—
а_с.
Поскольку
точки 3 и 4 показываются с внут­ренней
стороны поверхности, то их нормали
совпадают по направлению с нормалями
соответственно в точках 1 и 2. Поэтому φ
₃
=
φ
₁
и
φ
₄
=
φ
₂.

Изображаемая
форма цилиндра не зависит от угла
поворота камеры а. Этот угол обуславливает
лишь закрашивание боковой поверхности
(наряду с уг­лами расположения¹
источника света). Учесть угол а можно,
если вычесть его из угла поворота
источника света. Рассмотрим алгоритм
графического вывода.

Находим
коэффициент отражения ki
= cos
<pi
sin
p_e

если
ki
< 0, то ki
= О

Находим
коэффициент отражения кг = cos
фг
sin
p_c

если
кг < 0, то кг = О

Находим
цвета clrl
и
clr2,
соответствующие
ki
и кг

Рисование
двух симметричных вертикалей задней
стороны:

вертикаль
от (хс+х,
ус-у — h/2)
до
(хс+х,
ус-у + h/2)
цветом
clr2
вертикаль
от (хс-х,
ус-у —
h/2)
до (хс-х,
ус-у + h/2)
цветом clrl

Рисование
двух симметричных вертикалей передней
стороны:

вертикаль
от (хс+х,
ус+у — h/2)
до (хс+х, ус+у + Ь/2) цветом
clrl
вертикаль
от (хс-х,
ус+у — h/2)
до
(хс-х,
ус+у + h/2)
цветом
clr2
}

Здесь
для упрощения записи алгоритма
использована идеальная диффузная модель
отражения света. Вначале определяются
коэффициенты ki
и к₂,
кото­рые затем можно использовать
для вычисления цвета, например, в виде
ком­понент R,
G,
В:

где
R_u,
G_u
и В_u
— компоненты описания цвета поверхности
цилиндра.

Вертикали
выводятся сначала для задней стороны
боковой поверхности, а затем для передней.
При использовании Z-буфера
порядок вывода безразличен.

Данный
алгоритм сложнее предыдущего. Здесь в
теле цикла выполняется значительное
количество медленных операций— кроме
корня квадратного вычисляется также и
арксинус. Это является недостатком
алгоритма с пози­ций быстродействия.
Положительной чертой алгоритма является
вычисление угловой координаты (φ),
которую
можно использовать для наложения
тек­стуры-развертки (карты,).

Наложение текстуры

В некоторой степени,
компьютерная графика — это создание
иллюзий. Тек­стуры наглядно это
демонстрируют (рис. 5.38). Разве бывают
кирпичи округ­лой формы? Крайний
справа цилиндр «выложен» именно
такими кирпичами. При наложении текстуры
плоская карта-развертка растрового
образца тек­стуры плавно искривляется,
следуя гладкой форме боковой поверхности.

Рис.
5.38. Наложение текстур на боковую
поверхность цилиндра

Попробуйте подобрать
текстуру, чтобы кирпичи выглядели
действительно плоскими, как в реальной
жизни. Однако тогда может оказаться
заметным искривление в другом ракурсе.
Текстура— это достаточно простой способ

изображения
сложных поверхностей, это начальный
уровень имитации мате риалов. В самом
деле, если строить модель каждого
отдельного кирпича вид углублений
шероховатой поверхности, то эта модель
будет намного сложней цилиндра. Таким
образом, для создания более или менее
правдоподобного изображения, которое
в отдельных случаях удается выдавать
в качестве реа­листичного, необходимо,
в первую очередь, подобрать соответствующую!
текстуру.

Кроме того, и для
текстурированных объектов очень важно
соблюдать зако­ны отражения. Если
убрать градиентную закраску у четырех
цилиндров, изображенных на рис. 5.38, то
для первых трех (кроме «кирпичного»)
почти полностью исчезнет иллюзия
объемности.

Поскольку текстура
чаще всего представляет собой оцифрованный
фотосни­мок реальных объектов,
сделанный с определенного ракурса
съемки, то текстурирование дает
удовлетворительный результат только
для соответствующих ракурсов показа.

Рассмотрим, как
наложить текстуру на боковую поверхность
цилиндра. Способ наложения определяется
типом алгоритма рисования. Если цилиндр
ри­суется как многогранник, то в этом
случае текстурирование выполняется
так, как нами уже было рассмотрено выше
для многогранников, аппроксими­рующих
шар. Алгоритмы рисования объектов в
виде многогранников и поли­гональных
сетей являются достаточно универсальными
и могут быть исполь­зованы для широкого
класса объектов.

Здесь мы рассмотрим
один способ наложения текстуры, специально
предна­значенный для цилиндра. В его
основе лежит способ рисования цилиндра
вертикалями, рассмотренный выше. На
рис. 5.39 показана одна из вертикалей
закрашивания поверхности.

Рис.
5.39. Наложение текстуры вертикалями

Общий
цикл рисования боковой поверхности
можно представить себе сле­дующим
образом. Вначале определяются координаты
текущей вертикали за­крашивания в
экранной системе координат. Пусть эти
координаты составля­ют (х,
у1)
— (х, у2). Необходимо
также вычислить угловую координату
этой вертикали {<р).
По
значению угла ср
определяем
координату Х
_Т

в
шаблоне тек­стуры

где
НоrТех
—
горизонтальный размер шаблона текстуры.
Угол φ
измеряется
в градусах.

Одна
вертикаль закрашивания (х,
у1) — (х, у2) соответствует
вертикали с ко­ординатами {Х
_Т,
0)
— {Х
_Т,
VertTex
—
1) в шаблоне текстуры, где VertTex
—
раз­мер текстуры по вертикали.

Рисование
одной вертикали боковой поверхности
можно представить как цикл, в ходе
которого последовательно рисуются
пикселы с координатами от у1 до у2.
Для
пиксела в точке (x,
у)
определяются
соответствующие коор­динаты {Х
_Т,
Y_T)
в
шаблоне текстуры, причем Х
_Т

нам
уже известна, а коорди­ната Y_T
вычисляется
по формуле:

Затем
в шаблоне текстуры определяется цвет
точки {Х
_Т,
Y_T).
После
этого вы бранным цветом рисуется пиксел
с координатами(x,
у)
в
основном растре. Формулы вычисления
координат можно преобразовать к
следующему виду:

где
А,
В, С и
D
—
константы для всех пикселов одной
вертикали. Таким об разом, для каждого
пиксела вертикали приходится выполнять
несколько one
раций умножения и сложения. Для ускорения
текстурирования можно построить
Инкрементный алгоритм.

Данный
способ наложения текстуры можно
использовать только для простейших
цилиндров, расположенных вертикально.
При наложении текстур на более сложные
поверхности (в том числе вариации формы
цилиндра) следует применять полигональные
методы.

Вариации
формы цилиндра

Параметрические
формулы цилиндра удобно использовать
в качестве основы для описания поверхностей
достаточно сложной формы. В исходных
napf
метрических уравнениях цилиндра

величины
Н
и R
—
это константы. Рассмотрим примеры
поверхностей, когда! радиус R
является
функцией параметров h
и
l,
то есть R
— R(h,l).

Если
радиус зависит только от высоты, то есть
R
=
R{h),
то
это соответствуя поверхности вращения
относительно оси z.
Задание
конкретной функции R{h)
для
описания какой-либо поверхности
напоминает вытачивание цилиндрической
заготовки на токарном станке. На рис.
5.40 приведены примеры поверхностей
вращения (во всех случаях параметр h
изменяется
от -0.5 до +0.5).

где
R₁
и R₂
—
радиусы нижней и верхней части
соответственно. При R₂
=0
получаем конус. Очевидно, что при
аппроксимации многогранниками конус
следует рисовать уже не четырехугольными,
а треугольными гранями.

Рис.
5.40. Примеры поверхностей Рис.
5.41. Еще пример поверхности

вращения
вращения

Для
поверхности, изображенной на рис. 5.41,
при вычислении координат вершин
четырехугольных граней необходимо
использовать уже два цикла — по l
и по h.

M

Например:

В
данном случае вдоль вертикали располагаются
по две грани (dh
= 0.5).

В следующих примерах
для создания иллюзии гладкой поверхности
нужно использовать большее число граней
(рис. 5.42, 5.43).

Рис.
5.42. Сетка граней и закрашивание методом
Гуро

Рис.
5.43. Еще две поверхности вращения

Следующую
группу составляют такие вариации формы
цилиндра, когда ра­диус зависит только
от долготы, то есть R
=
R(l).
Пример
подобной поверх­ности показан на рис.
5.44.

И,
наконец, последнюю разновидность
вариаций данного типа, согласно на­шей
классификации, представляют поверхности
R
=
R(h,
l).
Пример
такой поверхности приведен на рис. 5.45.

Рис.
5.44. Другая разновидность вариаций формы
цилиндра

Рис.
5.45. Винтовая поверхность R
= R(h,
I)

Соседние файлы в папке KG

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

А зачем Вам это надо?

Дело в том, что потом надо будет ещё подставить сюда уравнение поверхности. И — скорее всего, нормировать этот вектор. И ещё домножить на плюс/минус, чтобы отобрать нужное из двух направлений. Но всё это имеет смысл обсуждать предметно лишь для конкретно поставленной задачи.

(впрочем, со знаками у Вас всё тривиально: на одной половинке цилиндра иксовая координата вектора нормали должна быть положительной, на другой — отрицательной)

Я работаю над лучей, и я собрался добавить цилиндры на сцену. Точка, за которую я застреваю, — это найти нормальный вектор поверхности в точке, в которую попадает луч. Мне нужно это, чтобы иметь возможность делать рассеянное освещение. То, что у меня на данный момент, — это трехмерная точка, в которой луч камеры попадает в цилиндр и фактический цилиндр, который определяется точкой на центральной оси, вектор, представляющий направление оси и радиус. Итак, чтобы подытожить мой вопрос, как найти нормальный вектор в точке, имеющей точку попадания цилиндра, радиус, точку на ее оси и вектор направления оси?