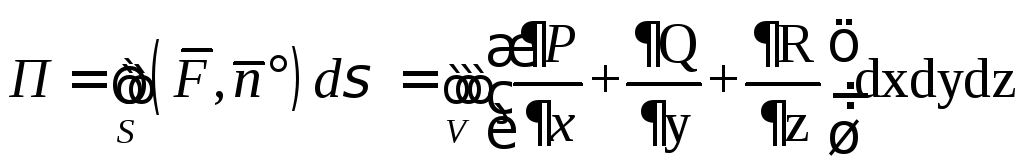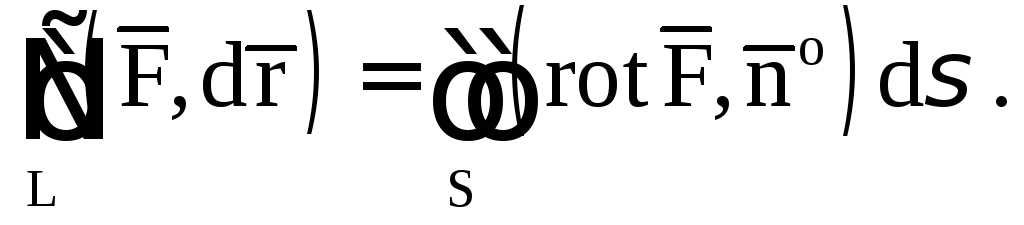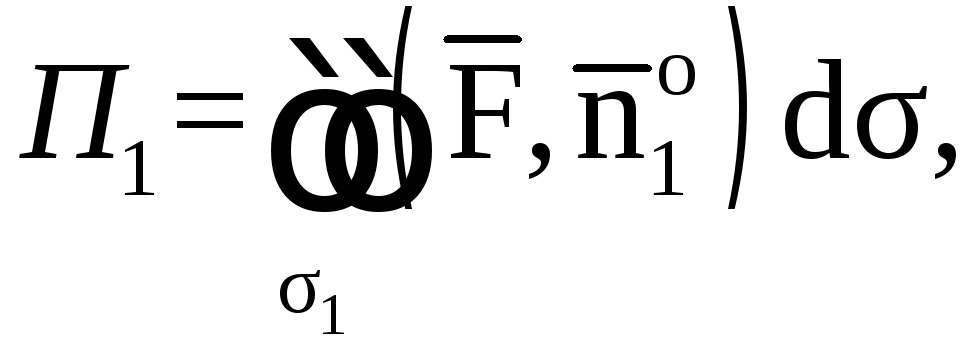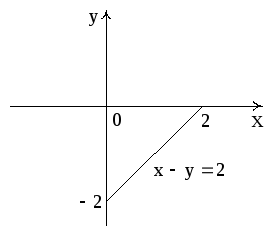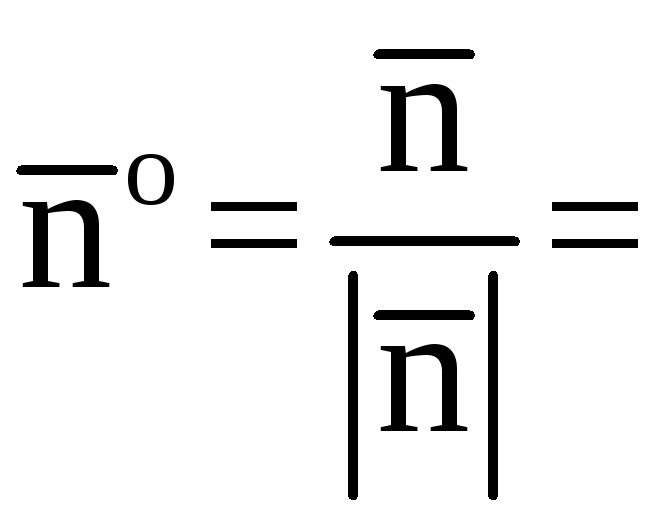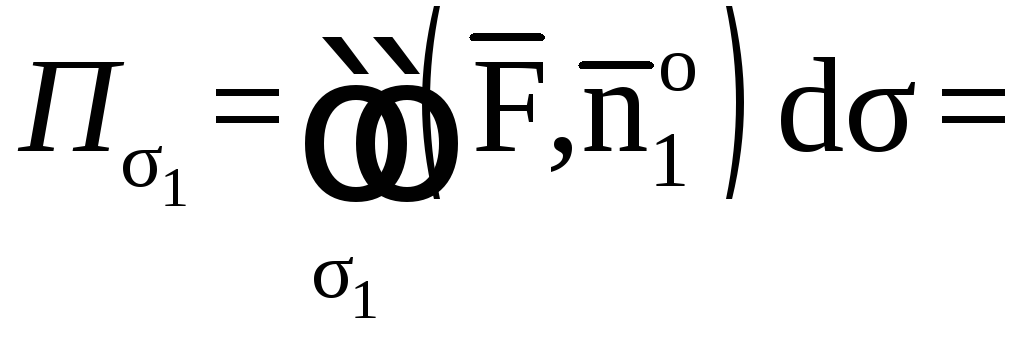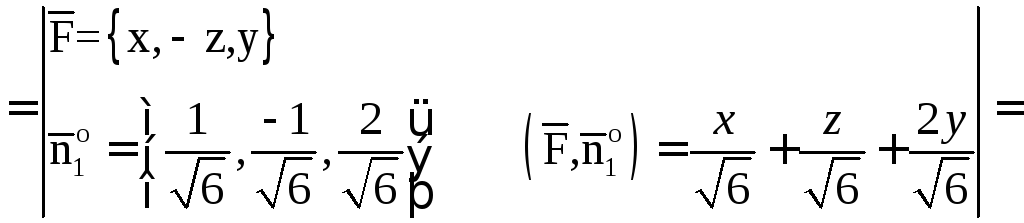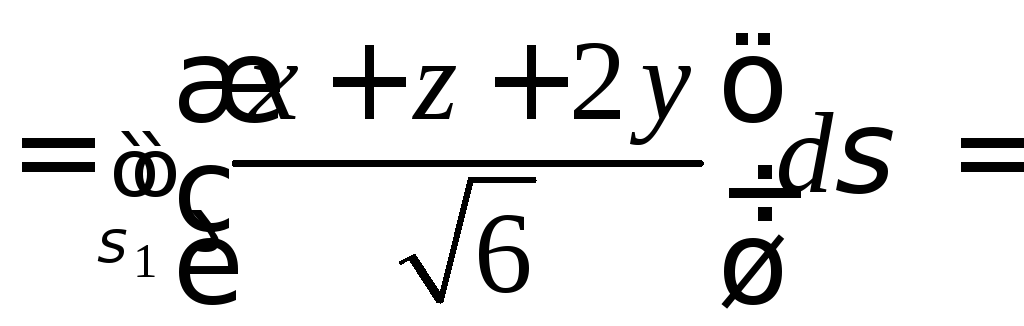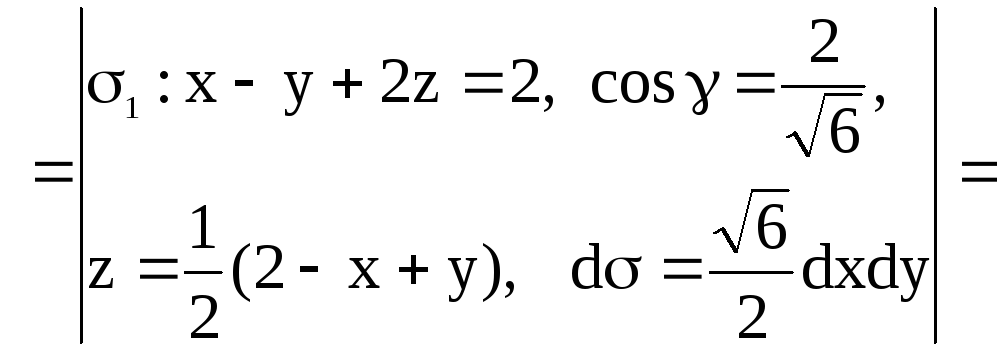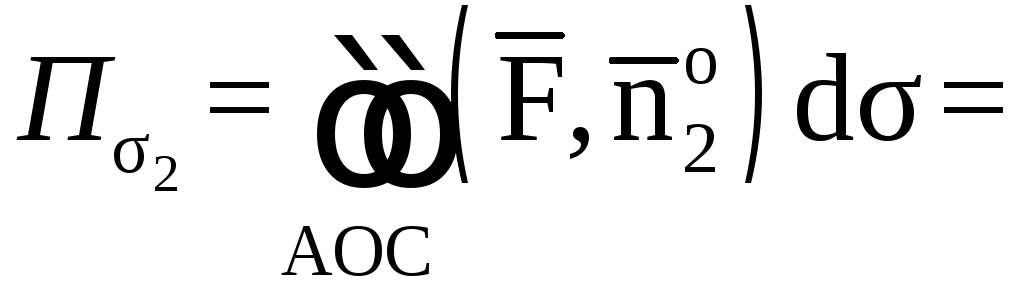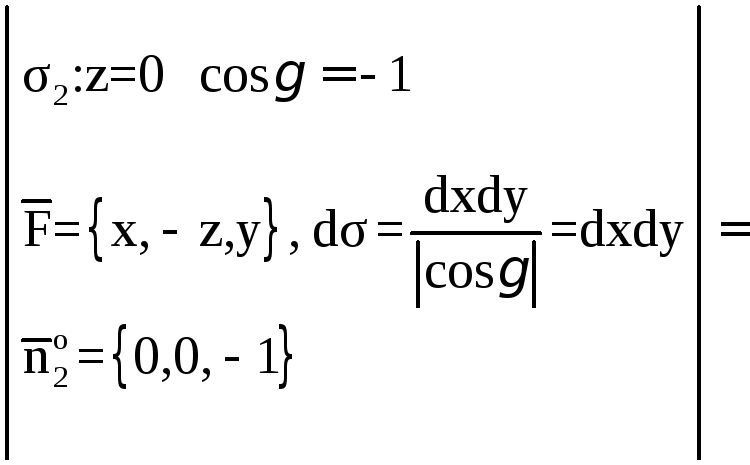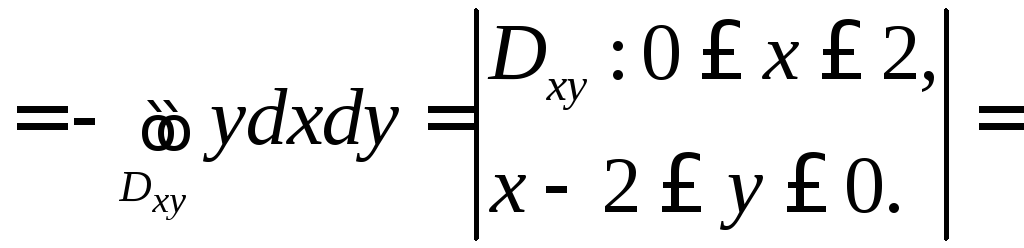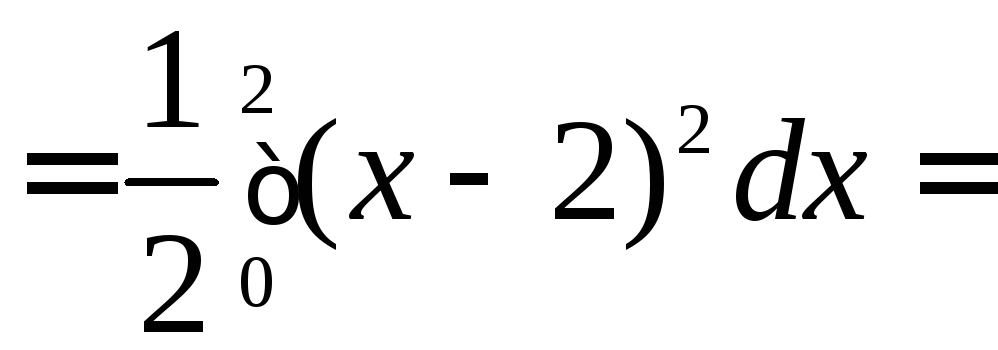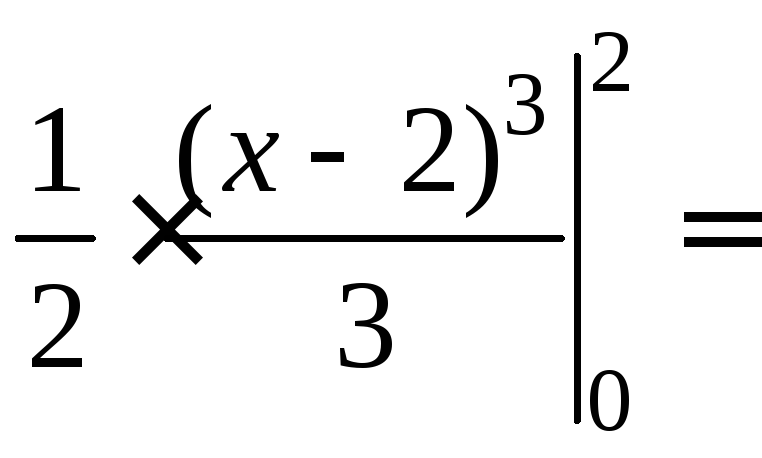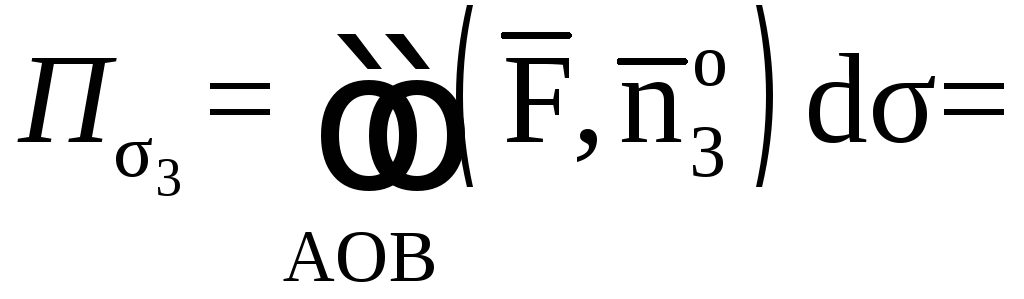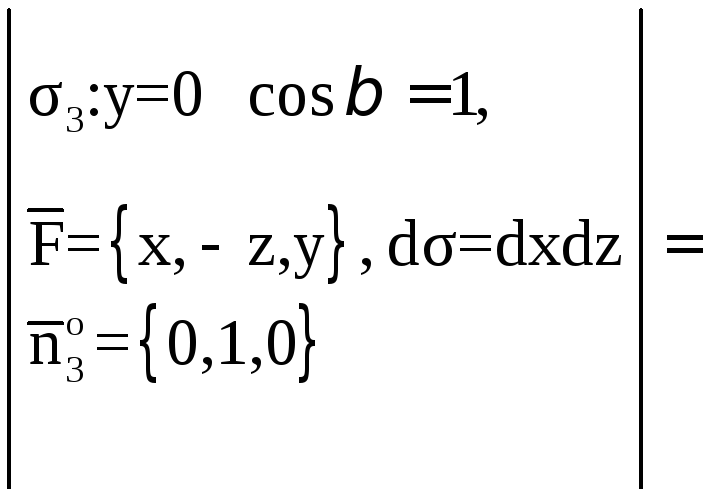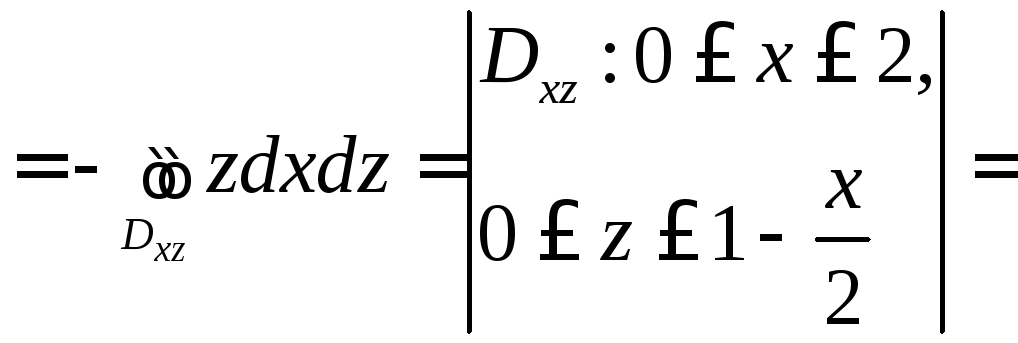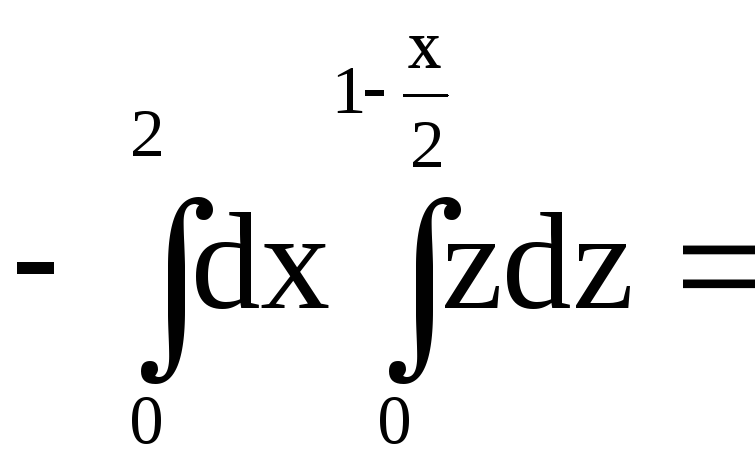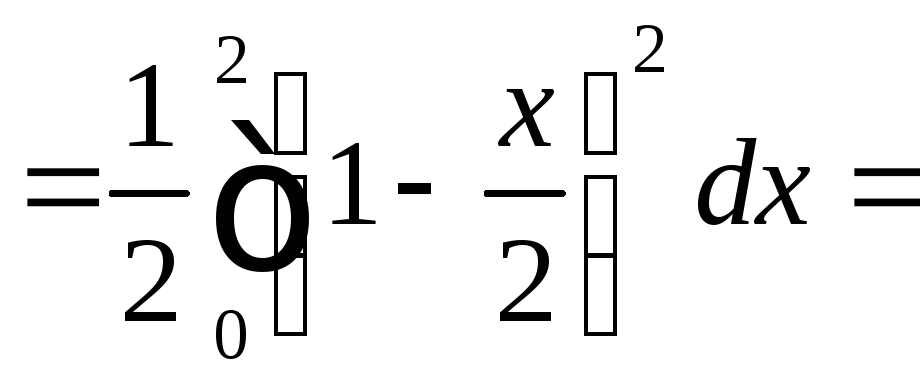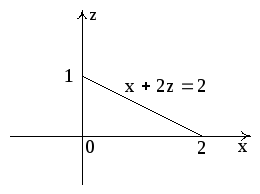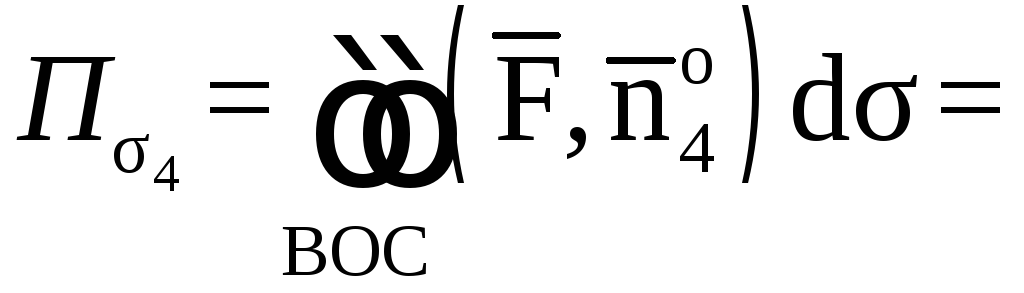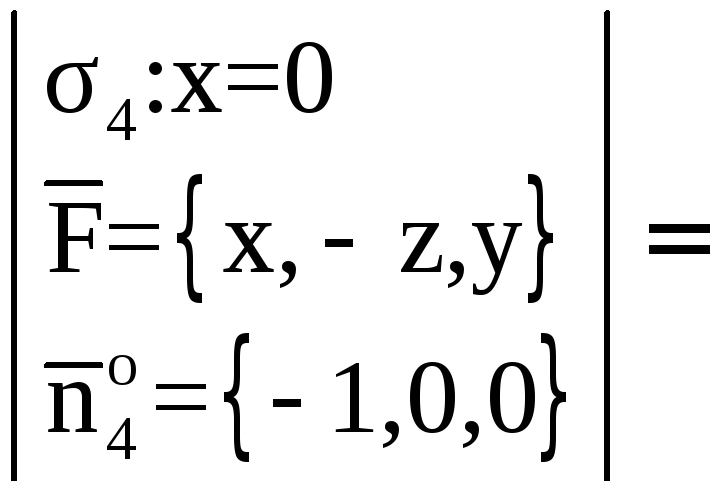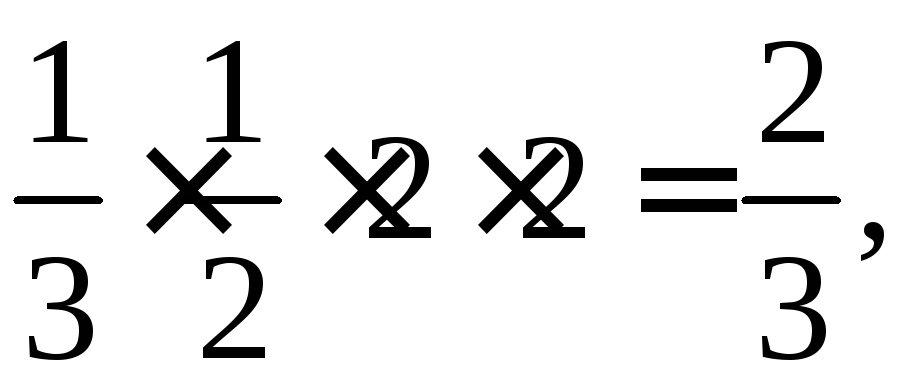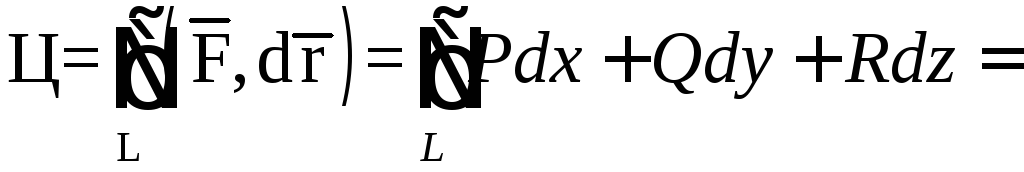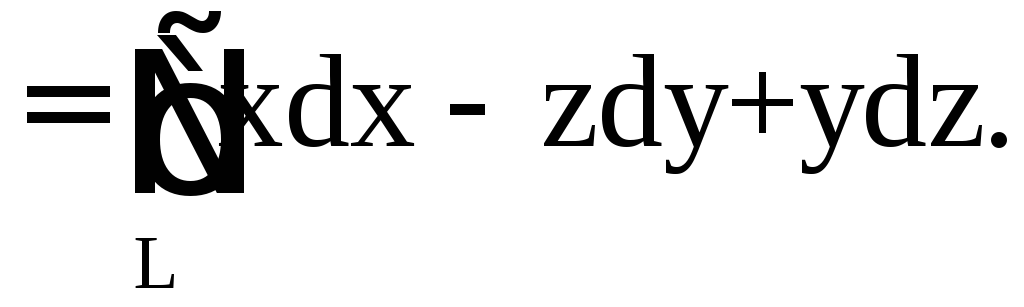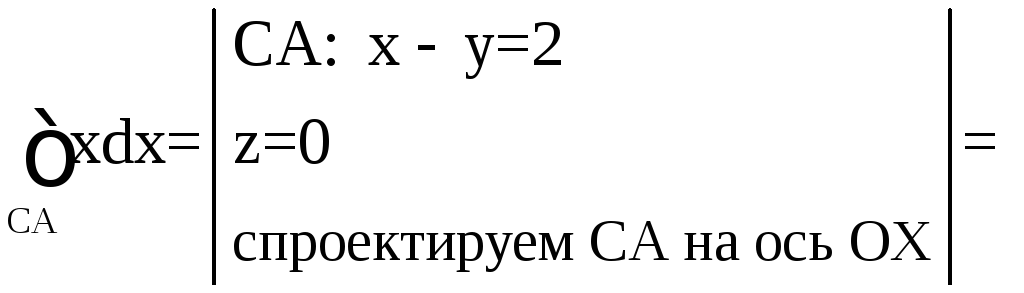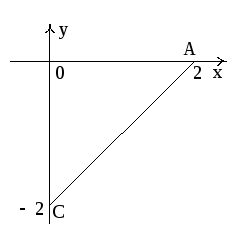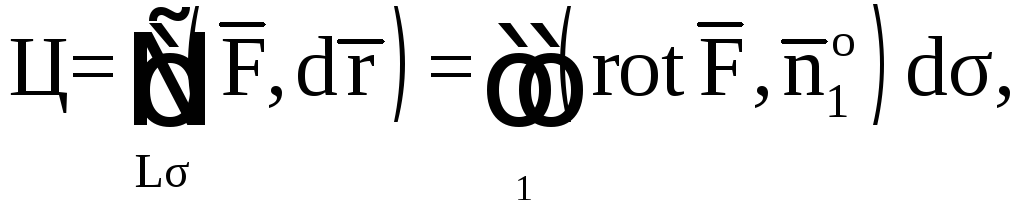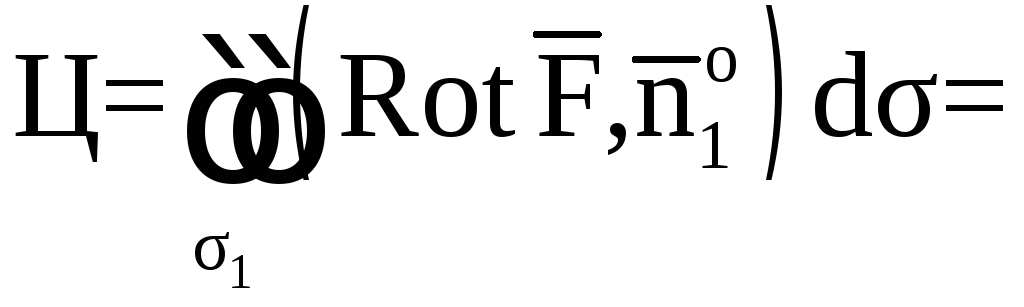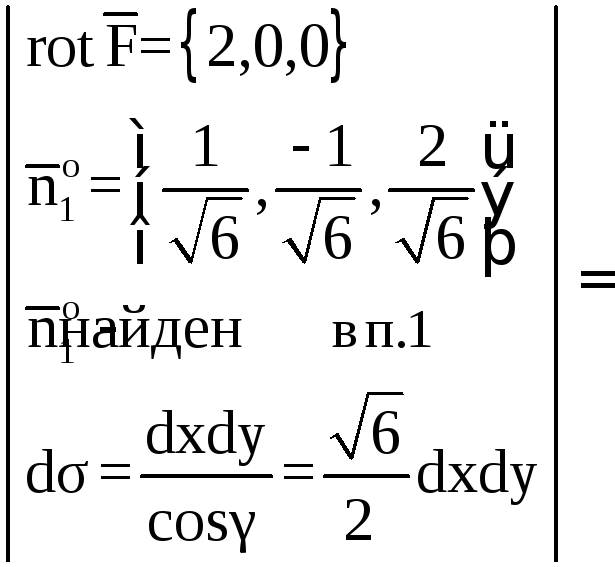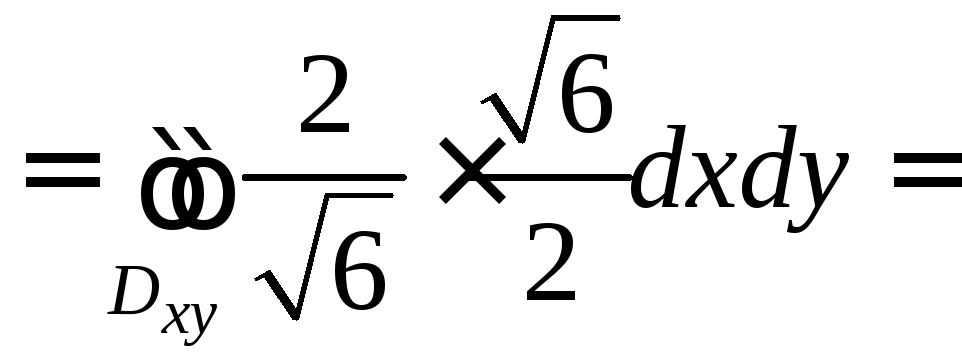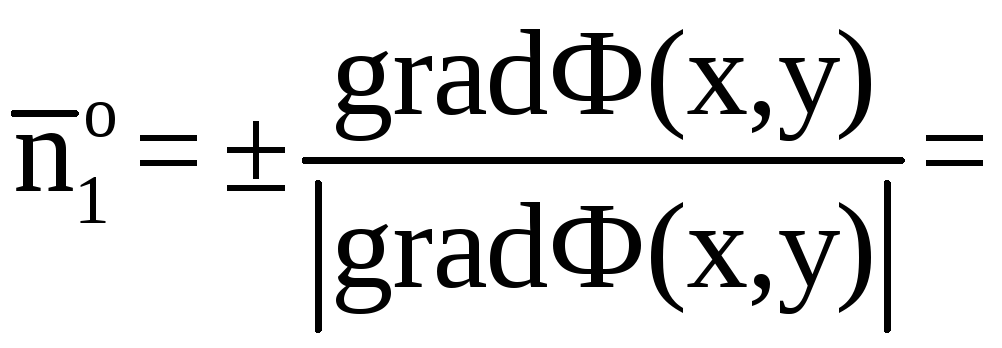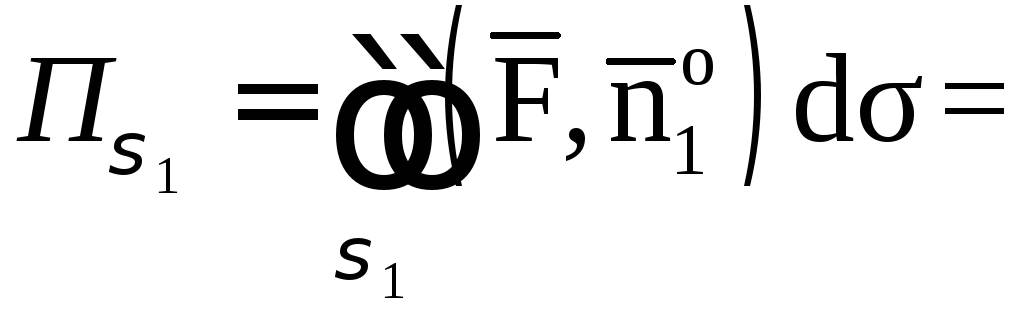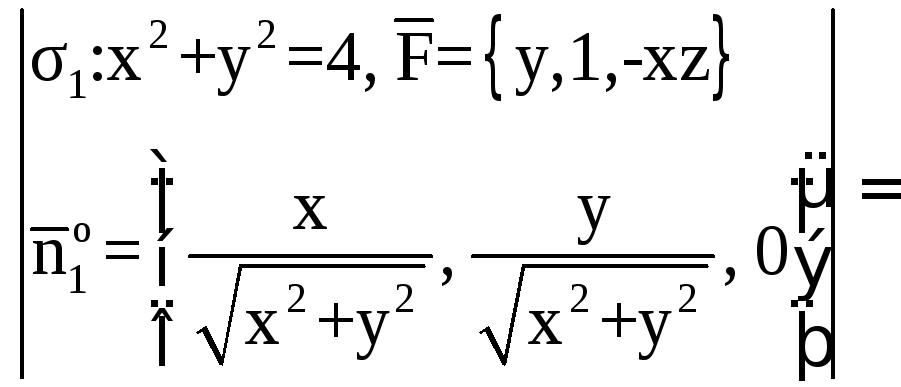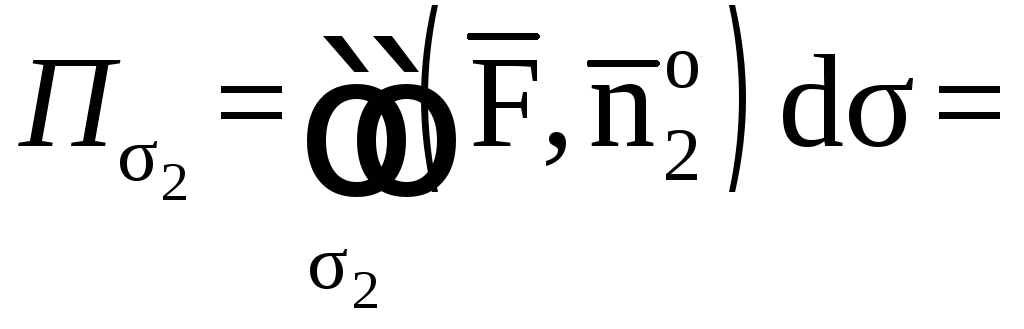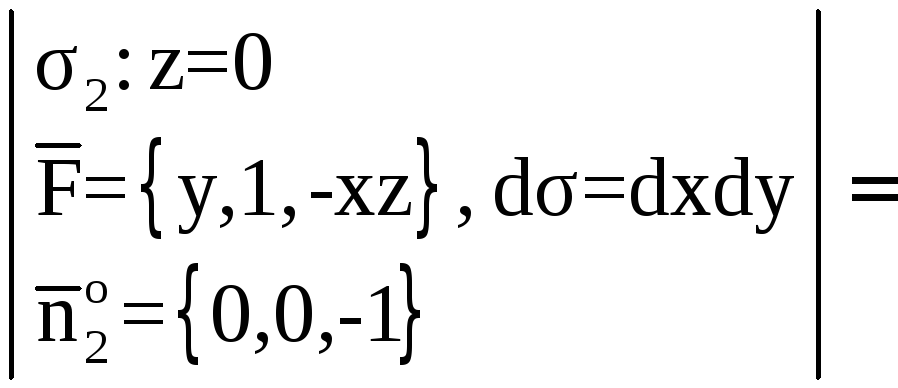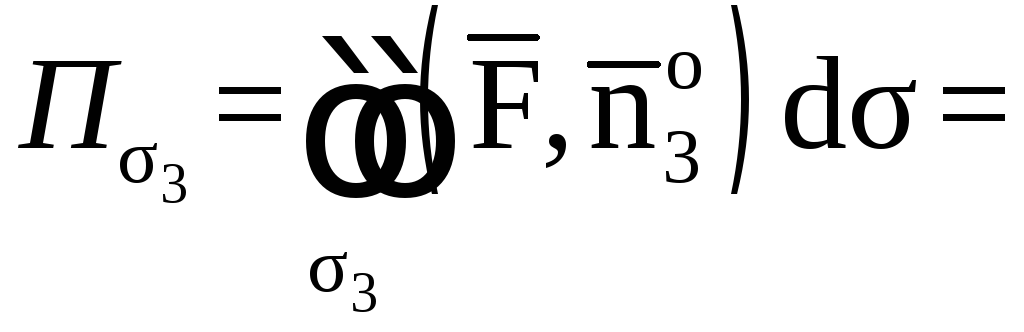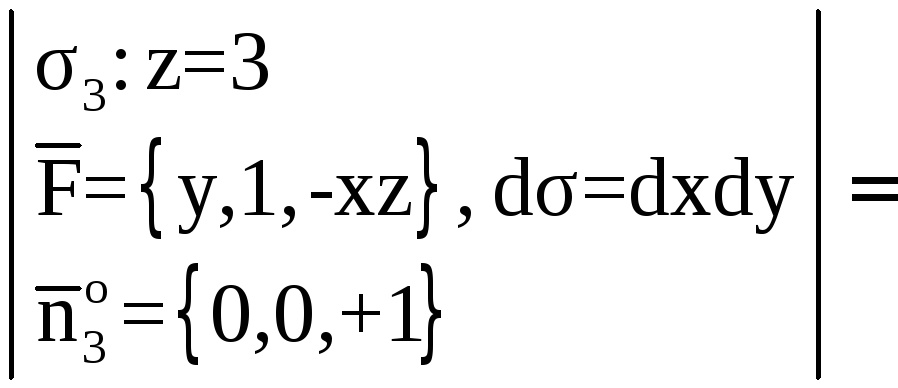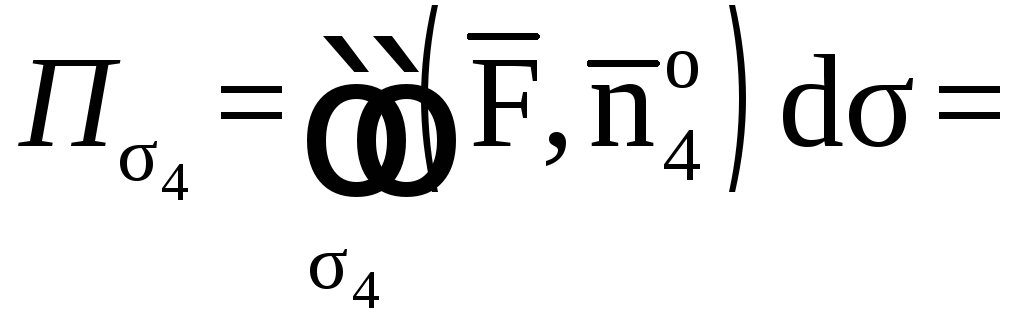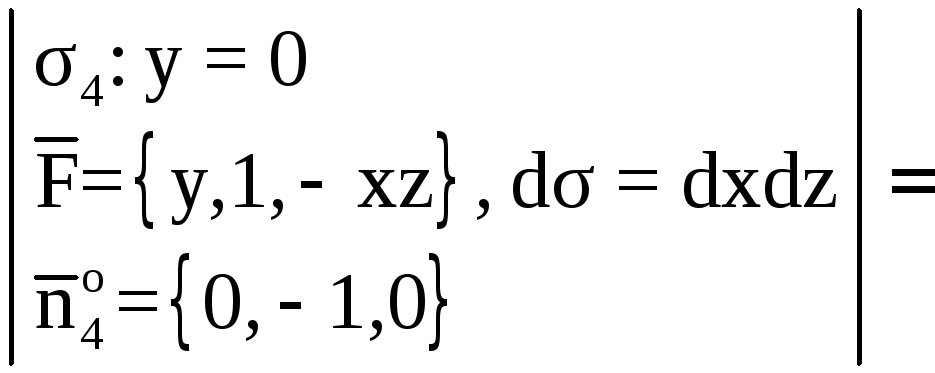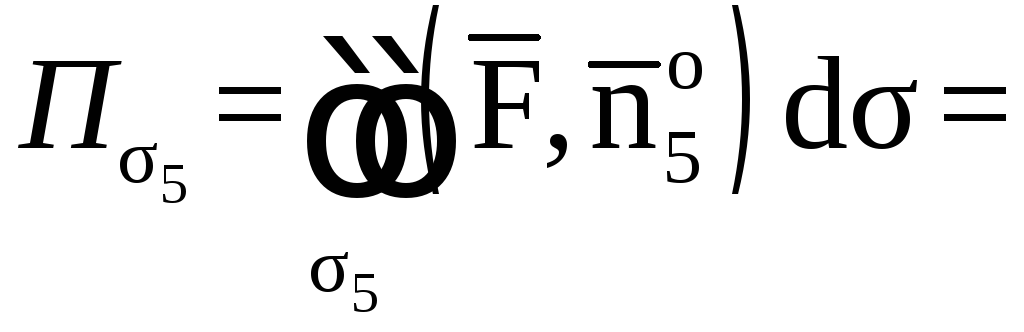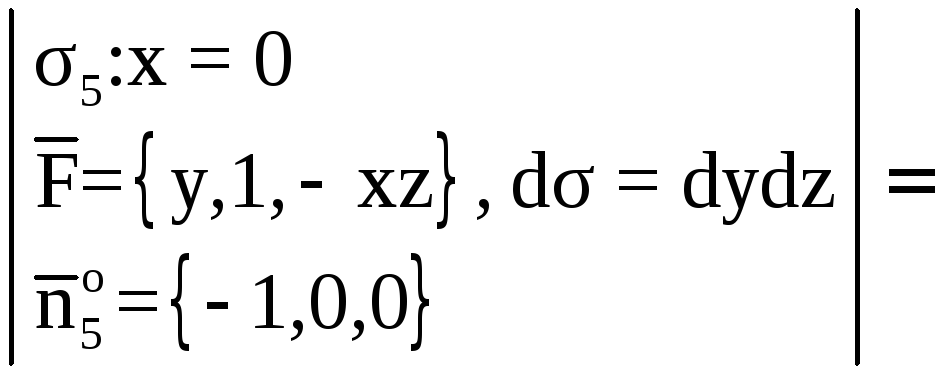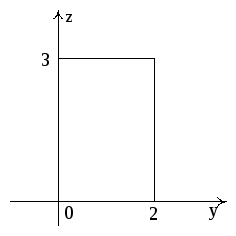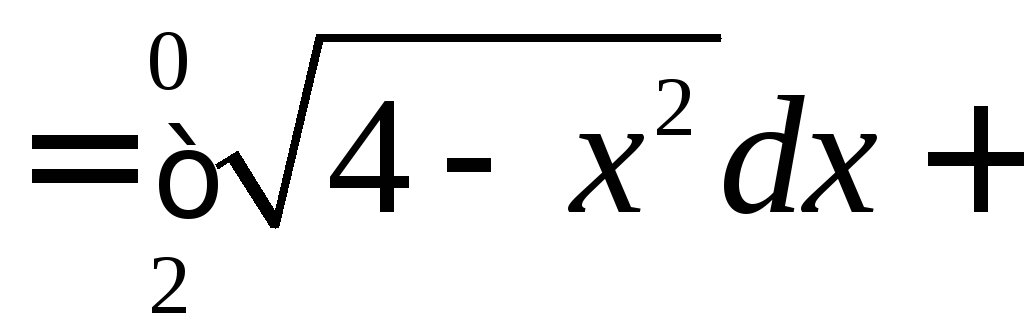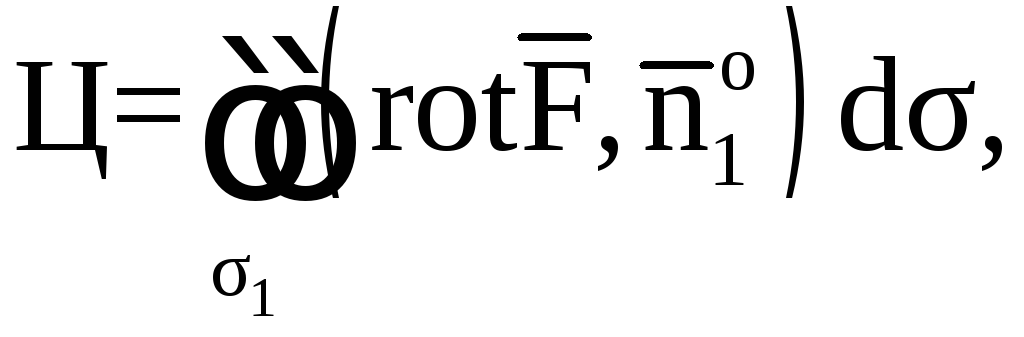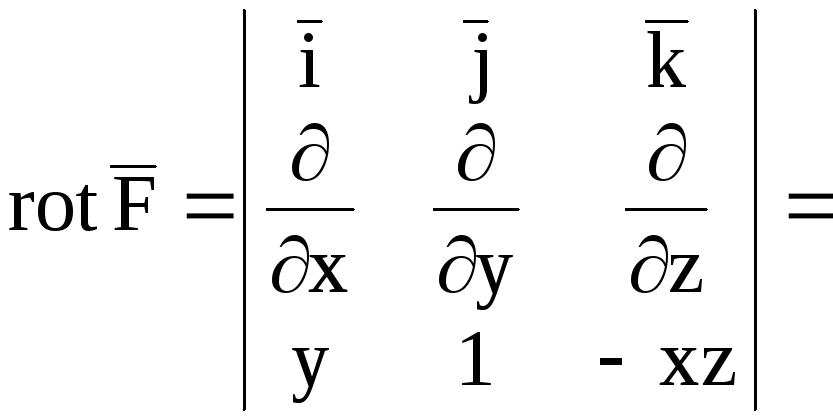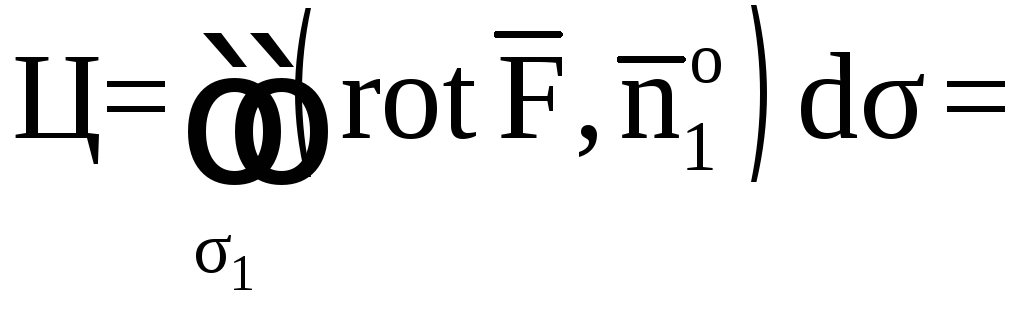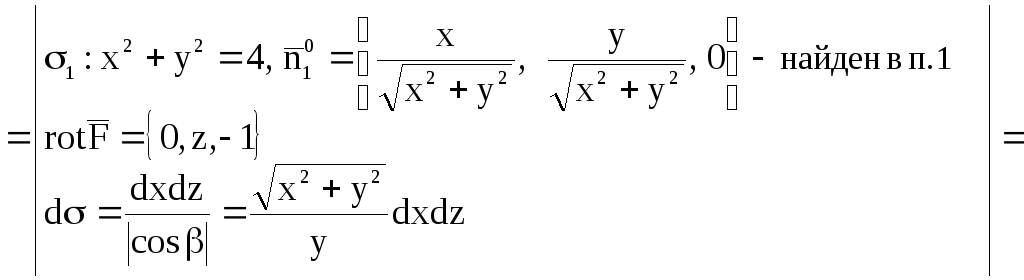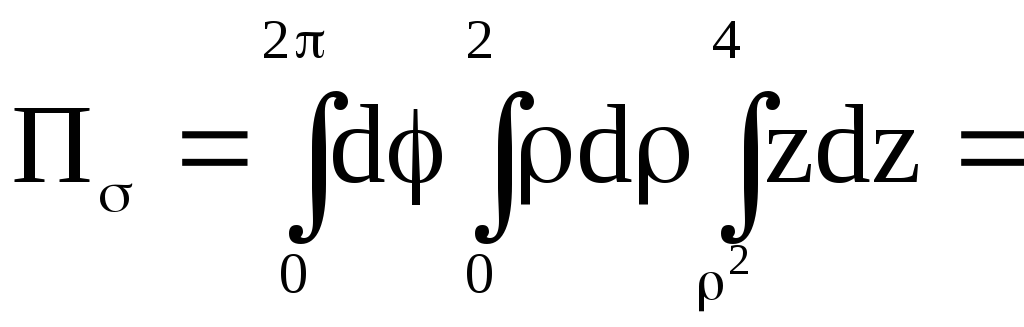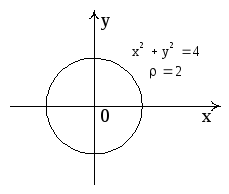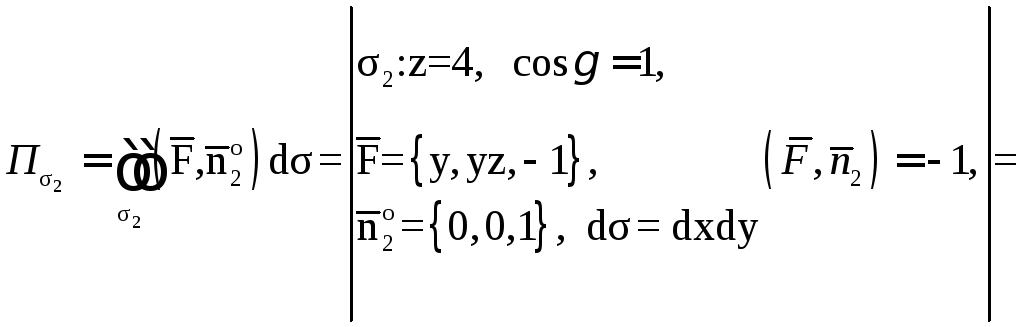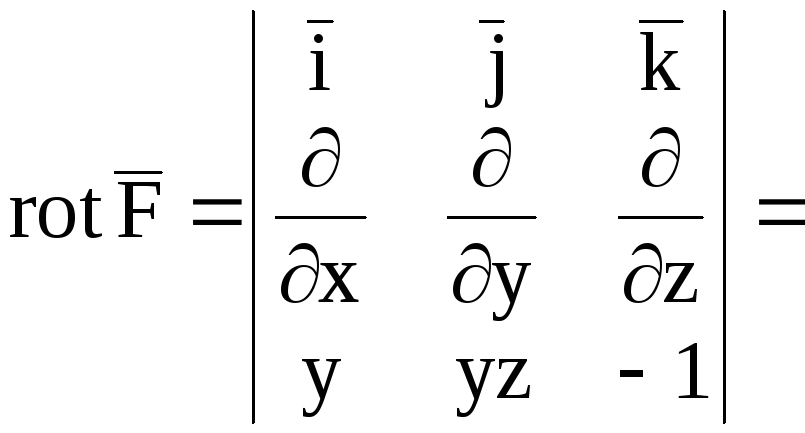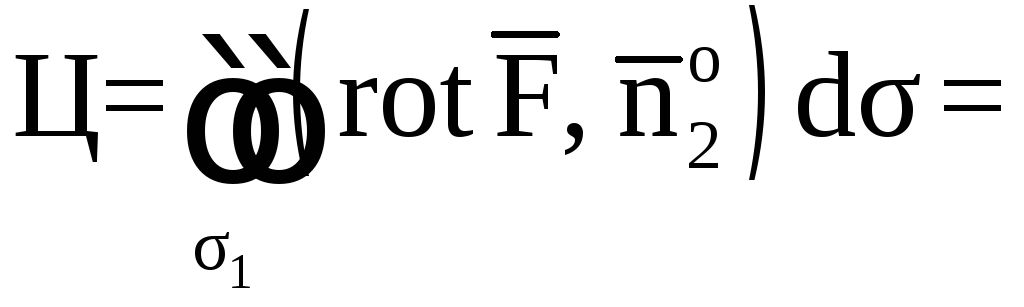Как найти нормаль к контуру

С механической точки зрения формулы eqref определяют гладкую (без разрывов и изломов) деформацию плоской области (Omega) в множество (Sigma) (простую поверхность в пространстве (boldsymbol^<3>)). Для практических целей только простых поверхностей недостаточно. Например, сфера (x^ <2>+ y^ <2>+ z^ <2>= a^<2>) не является простой поверхностью в (boldsymbol^<3>). Интуитивно ясно, что сферу нельзя получить никакой гладкой деформацией плоской области.

Имея в виду приложения теории поверхностных интегралов, введем в рассмотрение класс почти простых поверхностей.

Пусть (Omega) — плоская область и (F: overline <Omega>rightarrow boldsymbol^<3>) — непрерывно дифференцируемое отображение. Будем множество (Sigma = F(overline<Omega>)) называть почти простой поверхностью в (boldsymbol^<3>), если найдется расширяющаяся последовательность ограниченных областей (<Omega_>) таких, что (overline<Omega>_ subset Omega_), (Omega = displaystylebigcup_^<infty>Omega_) и поверхности (Sigma_ = F(overline<Omega>_)) простые.

Сфера (S = <(x, y, z): x^<2>+ y^ <2>+ z^ <2>= a^<2>>) есть почти простая поверхность.

(vartriangle) Введем сферические координаты. Тогда сфера (S) есть образ прямоугольника (overline <Omega>= displaystyleleft<(varphi, psi): 0 leq varphi leq 2pi, -frac<pi> <2>leq psi leq frac<pi><2>right>) при непрерывно дифференцируемом отображении (F: overline <Omega>rightarrow S), определяемом формулами
$$
x = a cos varphi cos psi,qquad y = a sin varphi cos psi,qquad z = a sin psi.nonumber
$$

Образами отрезков (varphi = varphi_<0>), (displaystyle-frac<pi> <2>leq psi leq frac<pi><2>) являются меридианы, а при (displaystyle|psi_<0>| Рис. 52.1

Конус (K = <(x, y, z): x^<2>+ y^ <2>= z^<2>>) есть почти простая поверхность.

(vartriangle) Введем цилиндрические координаты. Тогда конус (K) есть образ полуполосы
$$
overline <Omega>= <(r, varphi): 0 leq r Рис. 52.2

Легко проверить, что (overline<Omega>_ subset Omega_), (Omega = displaystylebigcup_^<infty>Omega_) и что поверхности (Sigma_ = F(overline<Omega>_)) являются простыми. Поэтому конус (K) — почти простая поверхность. (blacktriangle)

Если (Sigma) есть простая поверхность, заданная векторным уравнением eqref, а непрерывно дифференцируемые функции
$$
u = u(u’, v’), v = v(u’, v’), (u’, v’) in Omega’nonumber
$$
задают взаимно однозначное отображение замыкания области (Omega’) на замыкание ограниченной области (Omega), причем якобиан отображения
$$
frac<partial(u, v)> <partial(u’, v’)>= begindisplaystylefrac<partial u><partial u’>&displaystylefrac<partial u><partial v’>\displaystylefrac<partial v><partial u’>&displaystylefrac<partial v><partial v’>endnonumber
$$
отличен от нуля в (overline<Omega>’), то уравнение
$$
boldsymbol = boldsymbol (u(u’, v’), v(u’, v’)) equiv boldsymbol<rho>(u’, v’);quad (u’, v’) in Omega’,label
$$
определяет ту же простую поверхность, что и уравнение eqref. Уравнения eqref и eqref называют различными параметризациями поверхности (Sigma).

Как и в случае кривых, можно расширить класс параметризаций, допуская и такие замены параметров, при которых непрерывная дифференцируемость, взаимная однозначность и необращение в нуль якобиана отображения нарушаются на границе области. Тогда можно получить такие параметризации простой поверхности, задаваемые функциями, непрерывная дифференцируемость которых не имеет места на границе области (Omega).

(vartriangle) Переход от уравнений eqref к уравнениям eqref задается формулами
$$
u = a cos varphi cos psi,quad v = a sin varphi cos psi,quad (varphi, psi) in Omega’.label
$$

Якобиан отображения eqref равен (a^ <2>sin varphi cos psi) и обращается в нуль при (psi = 0), то есть на части границы области (Omega’). Это приводит к тому, что при переходе к параметризации eqref частные производные функции (z = sqrt-u^<2>-v^<2>>) стремятся к бесконечности при приближении точки (u, v) к окружности (u^ <2>+ v^ <2>= a^<2>). (blacktriangle)

Как правило, в дальнейшем для простых поверхностей будут рассматриваться только такие параметризации, которые задаются непрерывно дифференцируемыми на замкнутом ограниченном множестве функциями.

Криволинейные координаты на поверхности.

Пусть простая поверхность (Sigma) задана векторным уравнением eqref. Предположим, что область (Omega) выпукла, ([a, b]) есть проекция области (Omega) на ось (u). Если (u_ <0>= in (a, b)), то прямая (u = u_<0>) будет пересекаться с областью (Omega) по отрезку (u = u_<0>), (alpha leq v leq beta) (рис. 52.3). Образ этого отрезка при отображении eqref есть кривая
$$
boldsymbol = boldsymbol (u_<0>, v), alpha leq v leq beta,label
$$
лежащая на поверхности (Sigma). Будем называть ее координатной кривой (u = u_<0>). Придавая (u_<0>) все значения из отрезка ([a, b]), получим семейство координатных кривых (u = operatorname). Аналогично строится и семейство координатных кривых (v = operatorname).

Рис. 52.3

В силу взаимной однозначности отображения eqref каждая точка (A) поверхности (S) однозначно определяется как пересечение двух координатных кривых, (u = u_<0>) и (v = v_<0>). Пара чисел ((u_<0>, v_<0>)) называется криволинейными координатами точки (A) поверхности. Запись (A(u_<0>, v_<0>)) означает, что точка (A) поверхности (Sigma) задана криволинейными координатами ((u_<0>, v_<0>)).

Например, в сферических координатах часть сферы (x^ <2>+ y^ <2>+ z^ <2>= a^<2>), ограниченная двумя меридианами и двумя параллелями, задается в криволинейных координатах (varphi), (psi) следующим образом:
$$
varphi_ <1>leq varphi leq varphi_<2>,quad psi_ <1>leq psi leq psi_<2>.nonumber
$$

На сфере координатные кривые (varphi = operatorname) — меридианы, а координатные кривые (psi = operatorname) — параллели.

На прямом круговом цилиндре координатными линиями будут образующие цилиндра и окружности, получающиеся при пересечении цилиндра плоскостями, перпендикулярными образующей.

Вектор-функция (boldsymbol (u_<0>, v)) есть непрерывно дифференцируемая функция параметра (v), и, следовательно, координатная кривая (u = u_<0>), определяемая равенством eqref, является непрерывно дифференцируемой. Вектор (boldsymbol_ (u_<0>, v_<0>)) является касательным к этой кривой в точке (A(u_<0>, v_<0>)). Аналогично, вектор (boldsymbol_ (u_<0>, v_<0>)) касателен к координатной кривой (v = v_<0>) в точке (A(u_<0>, v_<0>)). Заметим, что векторы (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_ (u_<0>, v_<0>)) не могут обратиться в нуль, так как в этом случае ранг матрицы eqref будет меньше двух. Следовательно, для простой поверхности координатные кривые являются гладкими.

Если область (Omega) не является выпуклой, а точка ((u_<0>, v_<0>)) лежит внутри (Omega), то нужно взять выпуклую окрестность точки ((u_<0>, v_<0>)), лежащую внутри (Omega). Тогда образ этой выпуклой окрестности будет куском поверхности (Sigma) и координатные кривые можно строить на этом куске поверхности (локально).

Касательная плоскость и нормаль к поверхности.

Пусть (Sigma) есть простая поверхность, заданная уравнениями eqref или векторным уравнением eqref. Рассмотрим точку (A(u, v)) на поверхности (Sigma), где ((u, v)) — внутренняя точка области (Omega). Построим координатные линии (u = operatorname) и (v = operatorname), проходящие через точку (A(u, v)). Векторы (boldsymbol_ (u, v)) и (boldsymbol_ (u, v)) будут касательными к соответствующим координатным линиям.

В любой точке (A(u, v)) простой поверхности (Sigma) векторы (boldsymbol_ (u, v)) и (boldsymbol_(u, v)) неколлинеарны. Направление вектора (N = [boldsymbol_, boldsymbol_]) при изменении способа параметризации или не меняется, или изменяется на противоположное.

(circ) Рассмотрим вектор (N = [boldsymbol_, boldsymbol_]) во всех точках поверхности (Sigma). Тогда
$$
boldsymbol=beginy_&z_\y_&z_endboldsymbol + beginz_&x_\z_&x_endboldsymbol + beginx_&y_\x_&y_endboldsymbol.nonumber
$$
Если (boldsymbol = boldsymbol<0>), то все компоненты вектора (boldsymbol) равны нулю, и ранг матрицы eqref будет меньше двух, что невозможно для простой поверхности. Пусть поверхность (Sigma) параметризована двумя способами, eqref и eqref. Тогда, воспользовавшись правилом нахождения частных производных сложной функции и аддитивностью и кососимметричностью векторного произведения, получаем
$$
boldsymbol’ = [boldsymbol<rho>_, boldsymbol<rho>_] = [boldsymbol_ frac<partial u> <partial u’>+ boldsymbol_ frac<partial v><partial u’>, boldsymbol_ frac<partial u> <partial v’>+ boldsymbol_ frac<partial v><partial v’>] =\= [boldsymbol_, boldsymbol_] left(frac<partial u><partial u’>frac<partial v><partial u’>-frac<partial u><partial v’>frac<partial v><partial v’>right) = [boldsymbol_, boldsymbol_] frac<partial(u, v)><partial(u’, v’)>,nonumber
$$
то есть
$$
boldsymbol’ = boldsymbol frac<partial(u, v)><partial(u’, v’)>.label
$$
Так как якобиан (J = displaystylefrac<partial(u, v)><partial(u’, v’)>) не обращается в нуль в области (Omega’), то векторы (boldsymbol’) и (boldsymbol) коллинеарны. Эти векторы сонаправлены, если (J > 0), и противоположно направлены, если (J Лемма 2.

Вектор нормали к простой поверхности (Sigma) в точке (A(u_<0>, v_<0>)) ортогонален ко всем гладким кривым, лежащим на поверхности и проходящим через точку (A(u_<0>, v_<0>)).

(circ) В самом деле, такая кривая есть образ при отображении eqref некоторой гладкой кривой, лежащей в области (Omega) и задаваемой уравнениями (u = u(t)), (v = v(t)), (alpha leq t leq beta).

Уравнение кривой на поверхности тогда имеет вид
$$
boldsymbol = boldsymbol(u(t), v(t)), alpha leq t leq beta, u(t_<0>) = u_<0>, v(t_<0>) = v_<0>.
$$

Касательный вектор (boldsymbol<tau>) к этой кривой в точке (A) есть
$$
boldsymbol <tau>= frac

(boldsymbol(u(t_<0>, v(t_0))) = boldsymbol_(u_<0>, v_<0>) frac)>

+ boldsymbol_(u_<0>, v_<0>) frac)>

.nonumber
$$

Итак, (boldsymbol<tau>) есть линейная комбинация векторов (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_(u_<0>, v_<0>)). Так как вектор (boldsymbol) ортогонален (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_(u_<0>, v_<0>)), то он ортогонален и вектору (boldsymbol<tau>), то есть вектор нормали к поверхности в точке (A) ортогонален к любой гладкой кривой, лежащей на поверхности и проходящей через точку (A). (bullet)

Плоскость, проходящая через точку (A(u, v)) поверхности и ортогональная вектору (boldsymbol), называется касательной плоскостью к поверхности в точке (A). Пусть ((X, Y, Z)) — декартовы координаты точки касательной плоскости и пусть (boldsymbol = Xboldsymbol + Yboldsymbol + Zboldsymbol). Тогда векторы (boldsymbol-boldsymbol(u, v), boldsymbol_(u, v), boldsymbol_(u, v)) параллельны касательной плоскости, следовательно, их смешанное произведение равно нулю. Поэтому векторное уравнение касательной плоскости имеет вид
$$
(boldsymbol-boldsymbol(u, v), boldsymbol_(u, v), boldsymbol_(u, v)) = 0.nonumber
$$

В силу равенства eqref форма этого уравнения не зависит от выбора параметризации поверхности. Уравнение касательной плоскости в координатах имеет следующий вид:
$$
beginX-x(u, v)&Y-y(u, v)&Z-z(u, v)\x_(u, v)&y_(u, v)&z_(u, v)\x_(u, v)&y_(u, v)&z_(u, v)end = 0.nonumber
$$

Нормалью к поверхности в точке (A(u, v)) называется прямая, проходящая через точку (A) и параллельная вектору нормали в точке (A). Так как при изменении параметризации вектор нормали не меняет своего направления или изменяет его на противоположное в каждой точке поверхности, то нормаль не зависит от параметризации. Ее векторное уравнение имеет вид
$$
boldsymbol-boldsymbol(u, v) = k[boldsymbol_, boldsymbol_], -infty

Кусочно гладкие поверхности.

Из определения простой поверхности, данного в п. 1, следует, что она есть гладкий и взаимно однозначный образ некоторой плоской области, то есть получается из этой области при помощи гладких (без изломов) деформаций (отображений). Ясно, что многие объекты, которые мы привыкли называть поверхностями, не будут простыми поверхностями. Так, сфера не может быть непрерывным образом деформирована в плоскую область. Коническая поверхность не может быть получена гладкой деформацией плоской области.

Попытки дать общую классификацию поверхностей увели бы нас далеко в область высшей геометрии. Замечательным классом поверхностей в (boldsymbol^<3>) являются гладкие многообразия размерности 2, то есть связные множества, которые локально (в окрестности каждой своей точки) устроены, как простая гладкая поверхность. Например, сфера будет гладким многообразием. Если (A) есть точка сферы радиуса (a), то шар (S_<varepsilon>(A)) при (varepsilon Рис. 52.4

Из гладких кусков можно склеивать не только гладкие многообразия, но и связные поверхности, имеющие ребра и вершины (например, поверхности многогранников) (рис. 52.5).

Рис. 52.5

Мы не станем тут заниматься математической формализацией таких понятий, как разрезание и склеивание поверхностей, и тем более основанной на этом классификации поверхностей. Заметим только, что трудности возникают при построении общих теорий. В любом разумном частном случае нет проблем с разрезанием поверхности на простые куски. Поверхность, которую можно разрезать на конечное число простых кусков, будем называть кусочно гладкой.

Ориентируемые поверхности.

Будем говорить, что гладкая поверхность ориентируема, если можно построить на этой поверхности непрерывное поле единичных нормальных векторов. Говорят, что это поле единичных нормалей определяет ориентацию (или сторону) поверхности. Меняя направление всех единичных нормалей на противоположное, получим опять непрерывное поле единичных нормальных векторов. Говорят, что оно определяет противоположную ориентацию (другую сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов
$$
boldsymbol = frac<[boldsymbol_, boldsymbol_]><|[boldsymbol_, boldsymbol_]|>.label
$$

Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), так и неориентируемыми (односторонними).

Торы, изображенные на рис. 52.4, ориентируемы; бутылка Клейна — неориентируемая (односторонняя) поверхность. Легко построить лежащий на этой поверхности замкнутый гладкий контур такой, что, выбирая в какой-то точке контура вектор единичной нормали к поверхности и непрерывно изменяя его при движении по контуру, мы придем к начальной точке с противоположным направлением нормали. Следовательно, на бутылке Клейна построить непререрывное поле единичных нормальных векторов невозможно.

Заметим еще, что сфера, тор, тор с двумя дырами (рис. 52.4) делят пространство на ограниченную и неограниченную области, общей границей которых они являются. Бутылка Клейна таким свойством не обладает.

Можно доказать, что гладкая поверхность, являющаяся границей области в (boldsymbol^<3>), ориентируема. Ее внутренняя сторона задается нормальными векторами, направленными внутрь области (внутренними нормалями), внешняя сторона определяется внешними нормалями. Очевидно, что для построения поля внутренних нормалей к границе области достаточно построить внутреннюю нормаль к какой-то одной точке границы.

Рис. 52.6

Каждая плоскость делит пространство (boldsymbol^<3>) на два полупространства. Если плоскость рассматривать как границу полупространства, то внутренняя нормаль определяется естественным образом как направленная внутрь полупространства (рис. 52.6). Если (partial G) есть гладкая граница области (G), то касательная плоскость в точке (x in partial G) называется опорной, если область лежит по одну сторону от касательной плоскости, то есть в одном из полупространств, определяемых этой плоскостью. В точке (x in partial G) определена внутренняя нормаль (рис. 52.7).

Рис. 52.7

Границу области (G), ориентированную внешними нормалями, будем обозначать через (partial G), а внутренними — через (partial G^<->).

Несколько более сложно определяется ориентация кусочно гладких поверхностей.

Рис. 52.8

Пусть (Sigma) — простая поверхность (рис. 52.8), то есть гладкий и взаимно однозначный образ замыкания плоской области (Omega). В декартовых координатах отображение задается равенствами eqref. Прообразом гладкого простого контура (Gamma subset Sigma) будет простой гладкий контур (gamma subset Omega). Будем говорить, что контур (Gamma) ориентирован положительно, если его прообраз (gamma) ориентирован в плоскости ((u, v)) положительно (рис. 52.9), то есть при обходе контура (gamma) область, им ограничиваемая, остается слева (вектор касательной и вектор внутренней нормали образуют правую пару векторов в ориентированной плоскости ((u, v))). Будем говорить, что ориентация простой поверхности (Sigma), задаваемая полем единичных нормалей
$$
boldsymbol = frac<[boldsymbol_, boldsymbol_]><|[boldsymbol_, boldsymbol_]|>,nonumber
$$
согласована с положительной ориентацией простых контуров, лежащих на поверхности (Sigma).

Рис. 52.9

Покажем, что предложенное правило согласования ориентации поверхности с ориентациями простых контуров, лежащих на поверхности, совпадает с известным правилом правого винта. Пусть (A(u_<0>, v_<0>) in Sigma), то есть ((u_<0>, v_<0>) in Omega). Без ограничения общности можно считать, что (u_ <0>= 0), (v_ <0>= 0). Построим в точке (A)(0,0) касательную плоскость и ориентируем ее вектором нормали (boldsymbol) или, что то же самое, парой векторов ((boldsymbol_)(0, 0), (boldsymbol_)(0,0)). Возьмем в плоскости переменных (u), (v) окружность радиуса (varepsilon) с центром в точке (0,0):
$$
u = varepsilon cos t, v = varepsilon sin t, 0 leq t leq 2pi.nonumber
$$

Ее образ на поверхности есть простой замкнутый контур (Gamma):
$$
boldsymbol = boldsymbol (varepsilon cos t, varepsilon sin t), 0 leq t leq 2pi.nonumber
$$

С точностью до (boldsymbol(varepsilon)) при (varepsilon rightarrow 0) получаем, что
$$
boldsymbol = boldsymbol(0,0) + varepsilon boldsymbol_(0,0)cos t + varepsilon boldsymbol_(0,0)sin t + boldsymbol(varepsilon).nonumber
$$

С точностью до (boldsymbol(varepsilon)) кривая (Gamma) есть эллипс в касательной плоскости, ориентированной парой векторов ((boldsymbol_)(0, 0), (boldsymbol_)(0,0)).

Ориентация эллипса положительна (рис. 52.10). Если смотреть на касательную плоскость со стороны вектора нормали (boldsymbol), то движение по эллипсу происходит против часовой стрелки, от вектора (boldsymbol_)(0, 0) к вектору (boldsymbol_)(0, 0) (область, ограничиваемая эллипсом, остается слева).

Рис. 52.10

Пусть кусочно гладкая поверхность (Sigma) склеена из гладких простых кусков (Sigma_<1>, Sigma_<2>, ldots, Sigma_). Если склеивание происходит вдоль кривой (gamma), то после удаления концов кривой (gamma) она входит в края двух и только двух поверхностей (Sigma_). Кусочно гладкая поверхность (Sigma) называется ориентируемой, если можно так ориентировать гладкие куски (Sigma_), (i = overline<1, n>) что после согласования ориентации (Sigma_) с ориентациями (partial Sigma_) любая кривая склейки будет входить в состав краев соответствующих двух поверхностей с противоположными ориентациями (рис. 52.11).

Рис. 52.11

Можно показать, что кусочно гладкая поверхность, являющаяся границей ограниченной области, ориентируема, при этом каждый ее гладкий кусок можно ориентировать внутренними нормалями. В дальнейшем мы будем рассматривать только ориентируемые гладкие и кусочно гладкие поверхности.

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

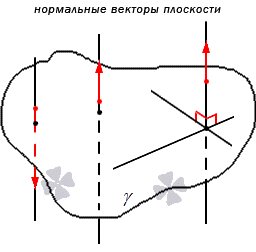
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

источники:

http://univerlib.com/mathematical_analysis/curve_surface_integrals/surfaces/

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-ploskosti-koordinaty-normalnogo-v/

Как найти нормаль плоскости

Нормаль плоскости n (вектор нормали к плоскости) – это любой направленный перпендикуляр к ней (ортогональный вектор). Дальнейшие выкладки по определении нормали зависят от способа задания плоскости.

Инструкция

Если задано общее уравнение плоскости — AX+BY+CZ+D=0 или его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то можно сразу записать ответ — n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.

Для получения общего ответа, вам понадобится векторное произведение векторов из-за того, что последнее всегда перпендикулярно исходным векторам. Итак, векторным произведением векторов, является некоторый вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом этот вектор (обозначьте его через n) ортогонален a и b – это главное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается против часовой стрелки.
[a,b] — одно из общепринятых обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, используется вектор-определитель (см. рис.1)

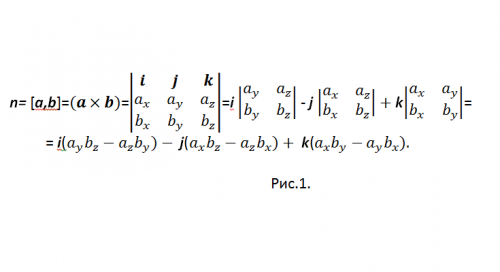
Для того чтобы не путаться со знаком «-», перепишите результат в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.
Более того, дабы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.

Вернитесь к решению поставленной задачи. Плоскость можно задать различными способами. Пусть нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно.
Пусть даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),
nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом,
nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль найдена — n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Если в некоторой
области G
пространства координаты вектора
непрерывны и имеют непрерывные частные
производныето

.

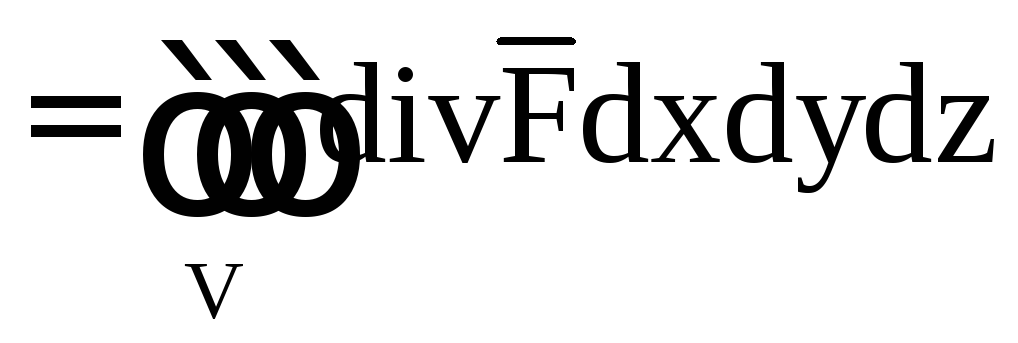
Здесь область
ограничена кусочно-гладкой поверхностьюS,
нормаль
к поверхностиS
берется внешняя.

4.3. Теорема Стокса

Пусть координаты
вектора

непрерывны и имеют
непрерывные частные производные. Тогда
циркуляция вектора
по замкнутому контуруL
равна потоку ротора этого вектора через
любую поверхность S,
натянутую на контур L

Предполагается,
что ориентация нормали
к поверхностиS
согласована с ориентацией контура L
так, чтобы из конца нормали обход контура
в выбранном направлении был виден
совершающимся против часовой стрелки.

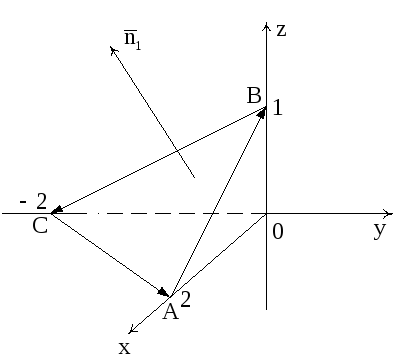
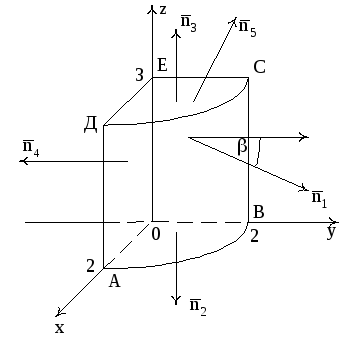
Пример 3.
Даны: векторное поле
и плоскость(P),
которая совместно с координатными
плоскостями образует пирамиду V.
Обозначим основание пирамиды, принадлежащее
плоскости (P),
через σ₁;
ограничивающий σ₁
контур – через L;
нормаль к σ₁,
направленную вне пирамиды V
– через
.

Требуется вычислить:

1) поток векторного
поля
через поверхность σ₁
в направлении нормали
;

2) поток векторного
поля
через полную поверхность σ пирамидыV
в направлении внешней нормали к ее
поверхности σ непосредственно и, применив
теорему Остроградского;

3) циркуляцию
векторного поля
по замкнутому контуруL
непосредственно и, применив теорему
Стокса к контуру L
и ограниченной им поверхности σ₁
с нормалью
.

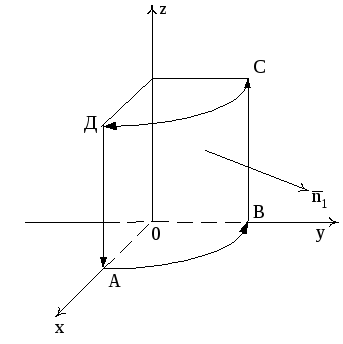
Решение.
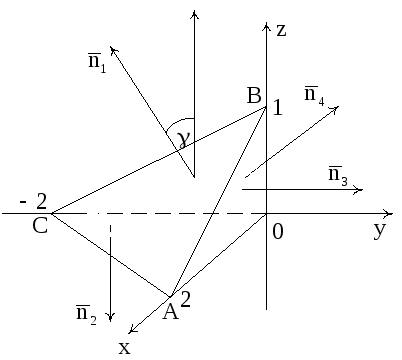
Сделаем чертеж. Для этого преобразуем
уравнение плоскости
к виду

.

Из этого уравнения
следует, что плоскость отсекает на осях
0X,
0Y,
0Z
соответственно отрезки
,(рис. 7).

Рис. 7

Эта и координатные
плоскости образуют пирамиду V
с основанием σ₁
(∆ АВС), а ограничивающий σ₁
контур обозначен через L.

1. Вычислим поток
векторного поля
через поверхность σ₁
в направлении
нормали
.

Спроектируем
поверхность σ₁
на плоскость X0Y
в область D_xy.

Поток найдем по
формуле

где
единичный вектор нормалинаправленный вне пирамиды (рис.7). По
условию нормаль к плоскостиимеет координаты.

Рис. 8

Тогда

Так как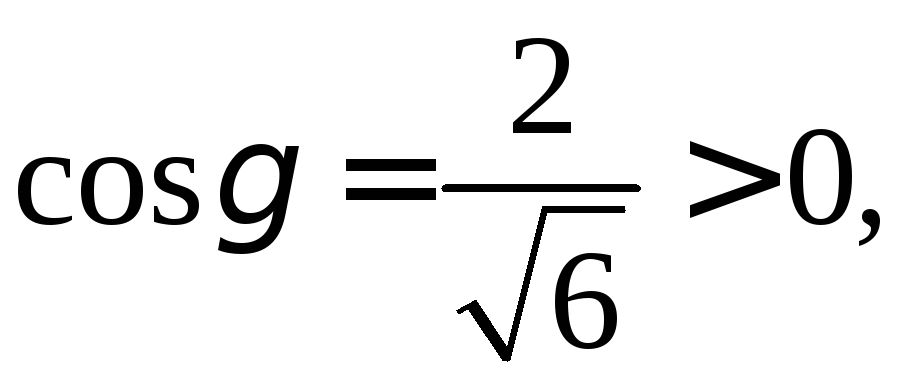то уголγ
между осью OZ
и
острый, нормальнаправлена вне пирамиды, что соответствует
выбранной стороне поверхности.
Следовательно, в качестве векторавозьмём вектор

Если
,
то в качестве векторанеобходимо взять вектор.

Элемент площади
.

Итак,

.

2. Вычислим поток
векторного поля
через полную поверхностьпирамидыV
в направлении внешней нормали к ее
поверхности непосредственно.

,

где ,,,

.

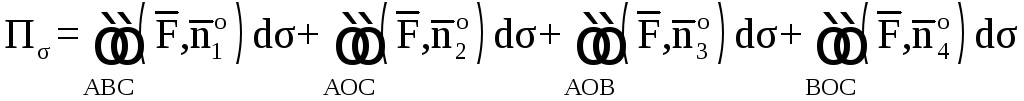
Вычислим каждый
поверхностный интеграл

уже найден.

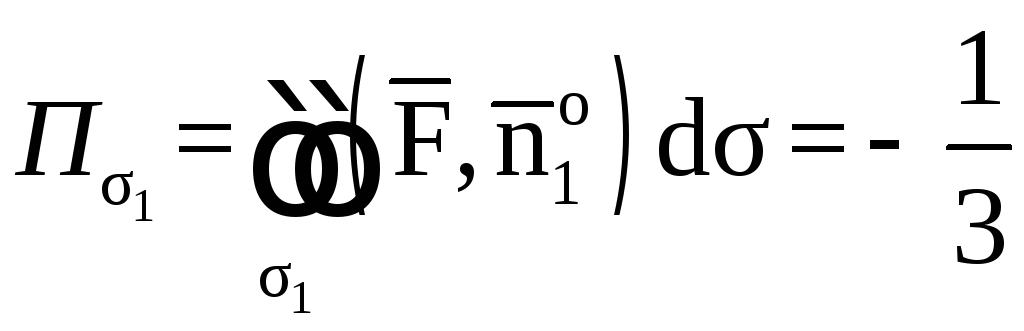
На гранях АОС, АОВ,
ВОС, соответственно

,
а единичные векторы внешней нормали к
этим граням
соответственно
равны

.

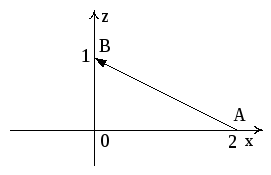
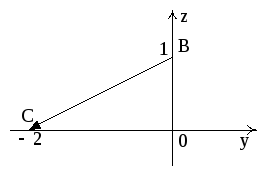
Заметим, что
уравнение прямой АС можно получить как
пересечение плоскости АВС и плоскости
ХОУ: z
= 0; АС: х у
= 2; Аналогично уравнение прямой АВ:x+2z=2.
Уравнение прямой ВС:

y+2z
= 2.

Поэтому
будем иметь:

;

;

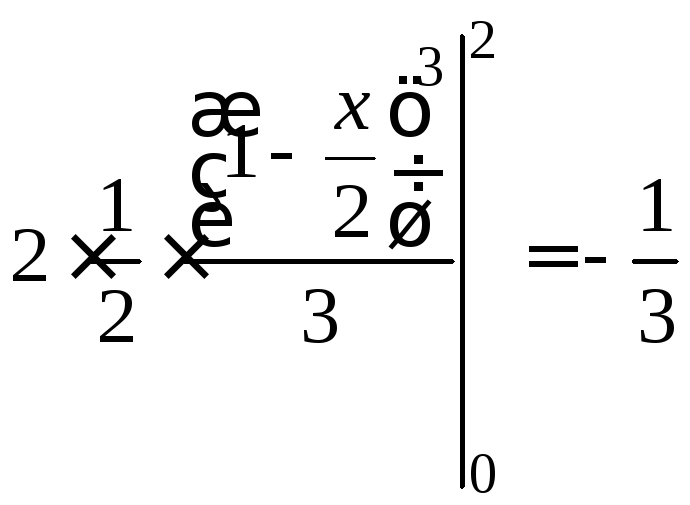
Рис. 9

.

Итак,
.

Вычислим поток
векторного поля
через полную поверхность пирамидыV,
применив теорему Остроградского:

.

где V
− объём пирамиды.

3. Вычислим циркуляцию
векторного поля

по контуру
треугольника ABCA,
где A(2,0,0),
B(0,0,1),

C
(0,–2,0), непосредственно (рис.10).

.

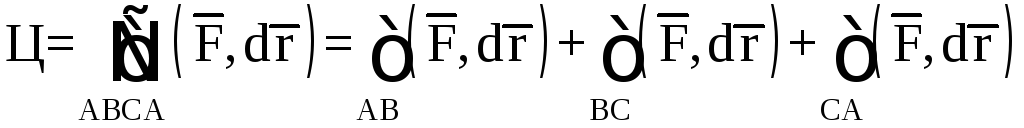
На AB:

на ВС:
;

на СА:
.

Рис. 10

Тогда
.

Вычислим каждый
интеграл в отдельности.

.

Рис. 11, а

Рис. 11,б

.

Рис.
11, в

Циркуляция по
контуру ABCA

.

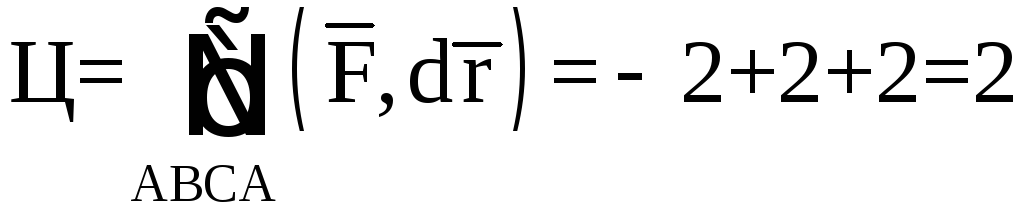
Найдем циркуляцию
векторного поля
по контуру треугольника АВСА, используя
формулу Стокса

где направление
обхода контура L
должно быть положительным, то есть
согласованным с ориентацией поверхности
.
В качествеберем верхнюю сторону треугольника
АВС, который расположен на плоскости.

В этом случае
нормальный вектор
к поверхностинаправлен вне пирамидыV
и из конца нормали
обход контураL
(АВСА) в выбранном направлении виден
совершающимся против часовой стрелки.

Находим

.

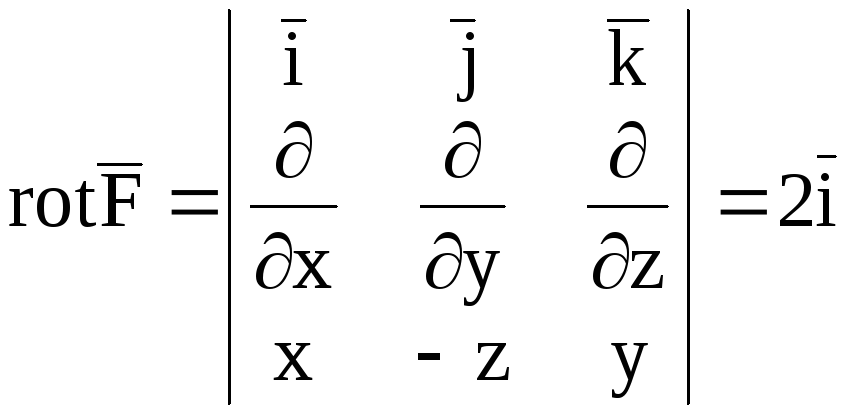
Тогда

,

где
−
площадь

Пример 4.
Даны: векторное
поле
и замкнутая поверхность,
составленная частью цилиндрической
поверхностии плоскостями,,,,

Поверхность
ограничена контуромL;
нормаль к поверхности,
направленная вне цилиндра.

Вычислить:

1) поток векторного
поля
через поверхностьв направлении;

2) поток векторного
поля
через замкнутую поверхностьв направлении внешней нормали к ее
поверхности непосредственно и применив
теорему Остроградского;

3) циркуляцию
векторного поля
по замкнутому контуруL
непосредственно, и применив теорему
Стокса к контуру L
и ограниченной им поверхности
с нормалью.

Сделать чертеж.

Решение.
Найдем поток векторного поля
через поверхностьДля этого спроектируем эту поверхность
на плоскостьXOZ
(проектировать поверхность
на плоскостьX0Y
нельзя, так как в этом случае ее проекцией
является линия) (рис. 12).

.

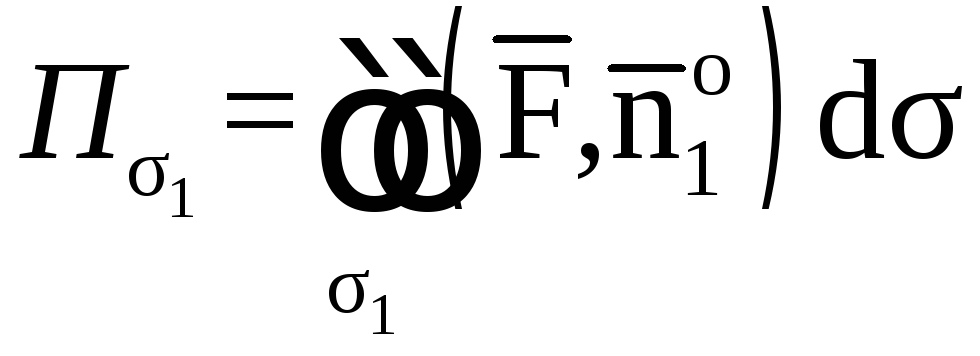
Рис. 12

Из рис. 12 видно,
что внешняя нормаль
образует острый угол β с положительным
направлением оси ОУ, то есть для заданной
стороны поверхностиЗапишем уравнение поверхностив виде

и найдем единичный
вектор нормали к ней (6).

.

Для того, чтобы
полученная нормаль
была внешней нормалью к цилиндрической
поверхности,
угол междуи осью ОУ должен быть острым.

В нашем случае
поэтому в полученной формуле для
нахожденияиз двух знаков (+) и (–) надо взять знак
минус.

Тогда
что соответствует выбранной внешней
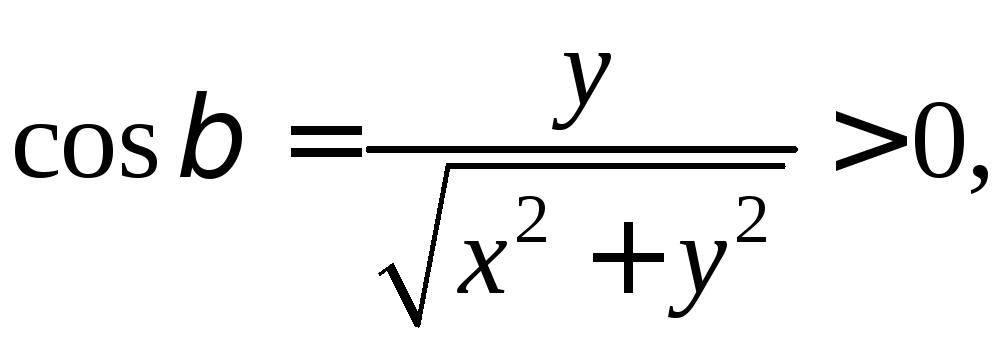
стороне цилиндрической поверхности.

Окончательно имеем
.

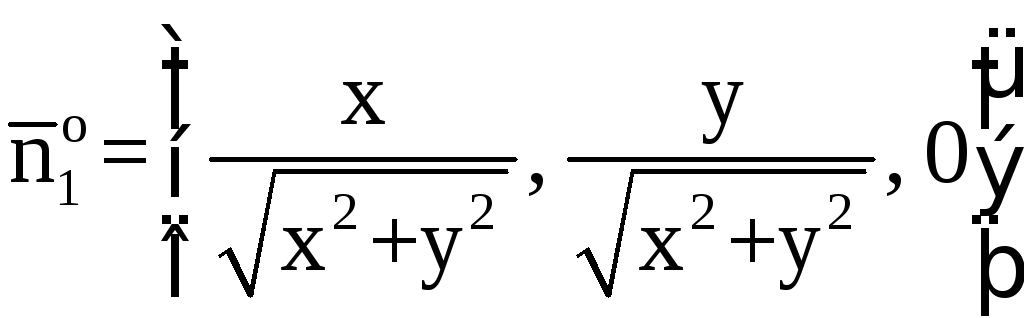
Элемент площади
.

Таким образом,

.

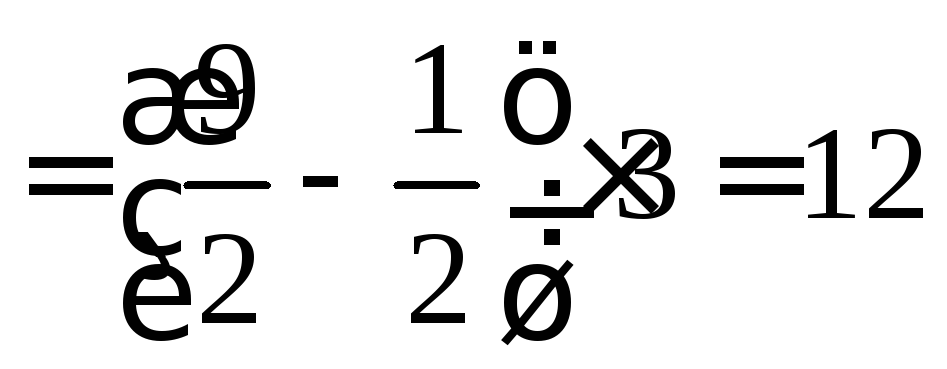
Рис. 12, а

Итак,
.

2) Найдем поток
векторного поля
через замкнутую поверхностьв направлении внешней нормали к ее
поверхности непосредственно.

,

где
,,,,

.

Итак,

, ;

Для вычисления
полученного интеграла перейдём в
полярную систему координат:
якобиан переходаТогда

=

, ;

Рис. 12, б

, ;

Рис. 12, в

, ;

Рис. 12, г

Суммарный поток
через замкнутую поверхность
равен

.

Найдем поток
векторного поля
через замкнутую поверхностьв направлении внешней нормали к этой
поверхности, применив теорему
Остроградского.

.

.

.

.

Тело V
проектируется на координатную плоскость
X0Y
в четверть круга. Поэтому целесообразно
этот интеграл вычислять в

цилиндрических
координатах.

Рис. 12, д

.

3) Найдем циркуляцию
векторного поля
по замкнутому контуруL
(ABCDA)
непосредственно. Контур L
состоит из четырех гладких линий AB,
BC,
CD,
DA.
Направление обхода контура ABCDA
примем положительным, то есть таким,
что с конца вектора
нормали к внешней стороне поверхностинаправление обхода по контуру было
видно совершающимся против часовой
стрелки (рис. 13)

Рис. 13

.

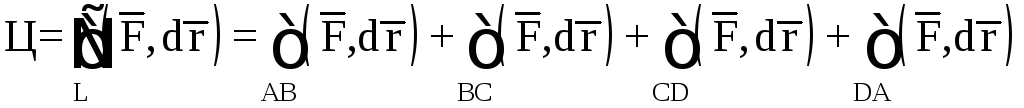
Так как
,
то.

На АВ:

;

на ВС:

,

,

;

на СД:

;

на DA:

,
,
,.

Тогда

.

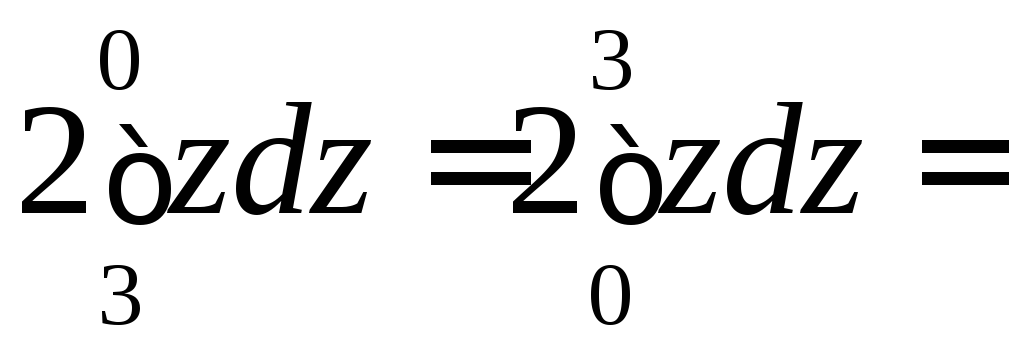
Найдем
циркуляцию векторного поля

по замкнутому контуру ABCDA,
применив теорему Стокса к этому контуру
и ограниченной им поверхности

с нормалью
.

По
теореме Стокса,

где направление обхода контура ABCDA
(L)
должно быть положительным. В качестве

берем внешнюю сторону части цилиндрической
поверхности, ограниченной контуром.

Находим

, .

.

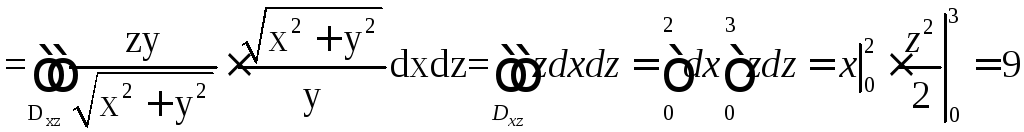
Пример
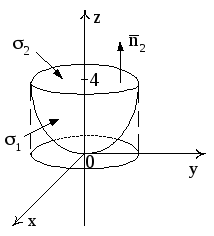
5. Даны
векторное поле
,
поверхность параболоида
,
отсеченная плоскостью

(рис. 14). Найти:

1)
поток вектора

через внешнюю сторону части поверхности

методом замыкания, применив теорему
Остроградского;

2)
Циркуляцию вектора

вдоль контура L
в положительном направлении, полученного
при пересечении поверхности

с плоскостью P,
применив теорему Стокса и непосредственно.

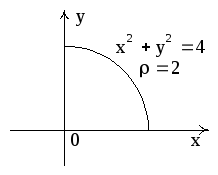
Решение.
1) Здесь
поверхность

незамкнутая, так что к ней нельзя
применить теорему Остроградского.
Однако вычисление потока по формуле

приводит к громоздким вычислениям.
Поэтому дополним заданную поверхность

поверхностью

.
Тогда получим замкнутую поверхность

,
состоящую из поверхностей

и

Очевидно, что
,
то есть

,

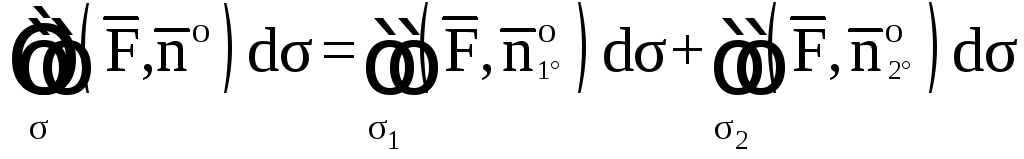
откуда
искомый поток
.

Вычислим

и

отдельно:
.

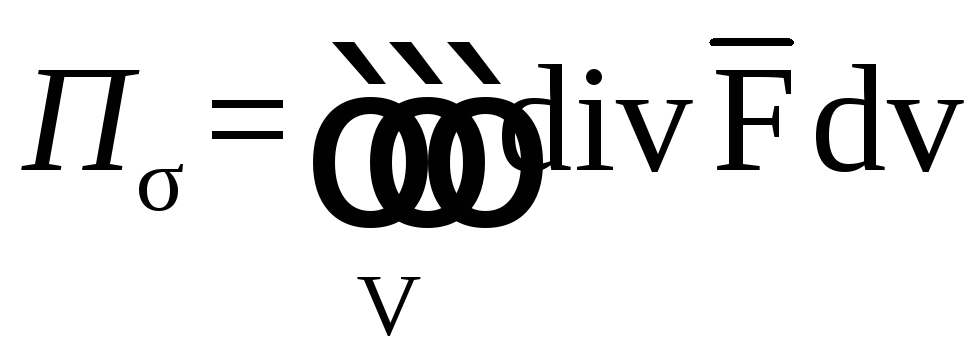
Так
как
,
то есть

то

Рис. 14

Тело
V
проектируется на плоскость X0Y
в круг. Вычислим этот интеграл в
цилиндрических координатах, в которых
уравнение параболоида

имеет вид
.

,

;

Рис.
15

.

Итак,

.

2)
Найдем циркуляцию вектора

вдоль контура L,
полученного при пересечении поверхности

с плоскостью

по теореме Стокса.

.

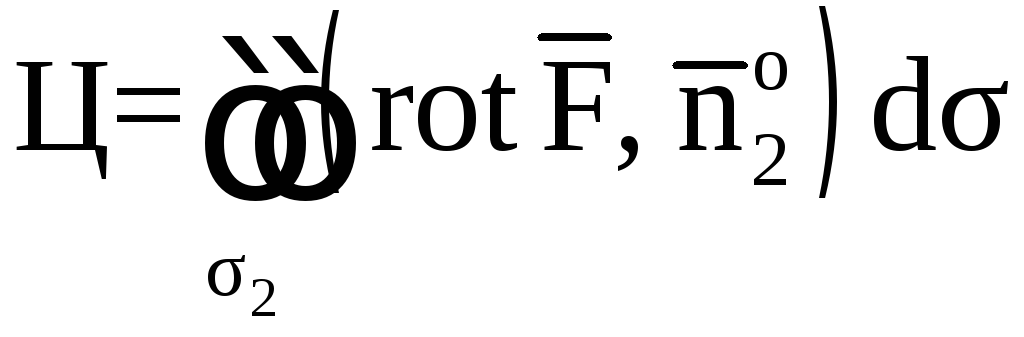
Найдем

.

.

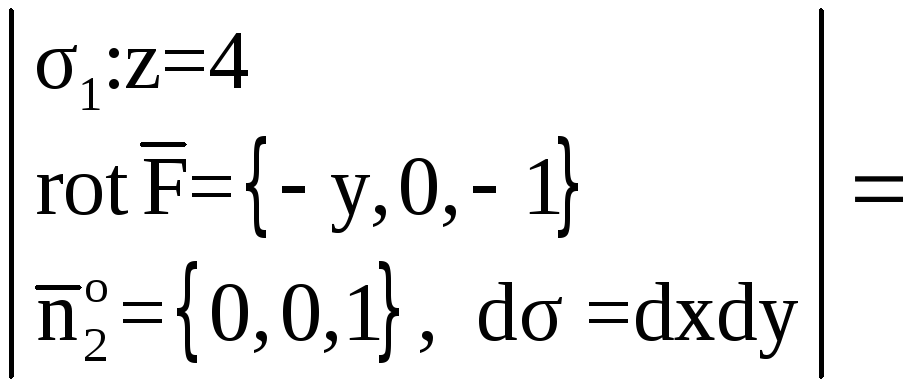
Найдем
циркуляцию вектора вдоль окружности

в положительном направлении непосредственно.

Параметрическое
уравнение контура L
имеет вид
,

,

,

.

Так
как
,
а
,
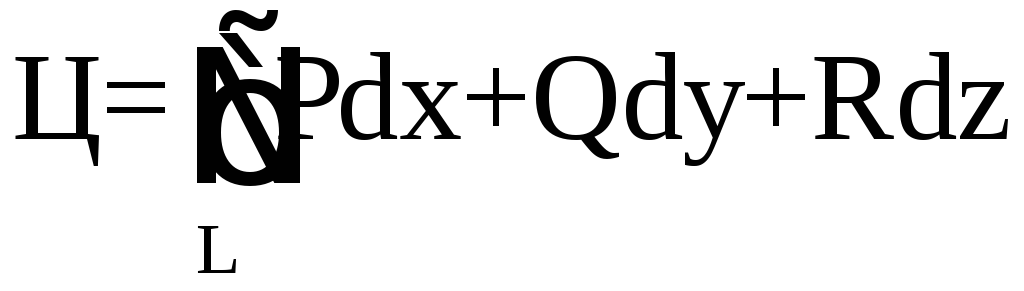
то

Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Если Ваш репетитор по математике имеет высокую квалификацию, то он должен это знать. В противном случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ по математике С1-С6 обычно включает разбор основных алгоритмов и формул, описанных ниже.

Угол между прямыми а и b

Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 180 град).

Какой алгоритм использует репетитор по математике для поиска угла?

1) Выбираем любые вектора и , имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов и по соответствующим координатам их начал и концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденный координаты в формулу:
. Для нахождения самого угла, нужно найти арккосинус полученного результата.

Нормаль к плоскости

Нормалью к плоскости называется любой вектор, перпендикулярный к этой плоскости.
Как найти нормаль? Для поиска координат нормали достаточно узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По этим координатам находим координаты векторов и и требуем выполнения условий и . Приравнивая скалярные произведение векторов к нулю, составляем систему уравнений с тремя переменными, из которой можно найти координаты нормали.

Замечание репетитора по математике: Совсем не обязательно решать систему полностью, ибо достаточно подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь из ее неизвестных координат любое число (например единицу) и решить систему двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то это значит, что в семействе нормалей нет той, у которой по выбранной переменной стоит единица. Тогда подставьте единицу вместо другой переменной (другой координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль будет иметь единицу по последней координате, а сама она окажется параллельной какой-нибудь координатной плоскости (в таком случае ее легко найти и без системы).

Угол между прямой и плоскостью

Допустим, что нам заданы прямая и плоскость координатами направляющего вектора и нормали
Угол между прямой и плоскость вычисляется по следующей формуле:

Угол между плоскостями

Пусть и  — две любые нормали к данным плоскостям. Тогда косинус угла между плоскостями равен модулю косинуса угла между нормалями:

Уравнение плоскости в пространстве

Точки, удовлетворяющие равенству образуют плоскость с нормалью . Коэффициент отвечает за величину отклонения (параллельного сдвига) между двумя плоскостями с одной и той же заданной нормалью . Для того, чтобы написать уравнение плоскости нужно сначала найти ее нормаль (как это описано выше), а затем подставить координаты любой точки плоскости вместе с координатами найденной нормали в уравнение и найти коэффициент .

Расстояние от точки до плоскости

Для вычисления расстояния от точки до плоскости , заданной уравнением можно использовать следующую формулу:

В знаменателе стоит длина нормали, а числителе — значение выражения из левой части уравнения плоскости в точке

Комментарий репетитора по математике:

Методом координат можно находить не только углы и расстояния в пространстве, но и
1) площади многоугольников (треугольника, параллелограмма), расположенных в заданной плоскости.
2) объемы простейших многогранников (параллелепипедов и пирамид).

Для понимания таких формул нужно изучить понятия векторного и смешанного произведения векторов, а также определителя матрицы. В скором времени я сделаю для вычисления объемов соответствующую справочную страничку.

Средства аналитической геометрии репетитор по математике практически не использует в работе со средним и тем более слабым учеником. И очень жаль, что загруженность среднестатистического сильного школьника не позволяет репетитору провести более-менее серьезную работу на уровне определений из высшей математики и с соответствующей практикой решения задач. Поэтому я часто ограничиваюсь простым сообщением формул и демонстрацией одного – двух примеров их использования. В школьной программе не предусмотрено время для изучения векторных приемов вообще, однако на ЕГЭ Вы имеете право решать задачу С2 любым из известных науке способов. Отсюда мораль: учите координаты. Расширенная подготовка к ЕГЭ по математике с изучением приемов аналитической геометрии даст Вам мощное и универсальное средство для решения огромного класса задач типа С2. Пользуйтесь этой страничкой на здоровье!

Колпаков А.Н. Репетитор по математике Москва (Строгино).