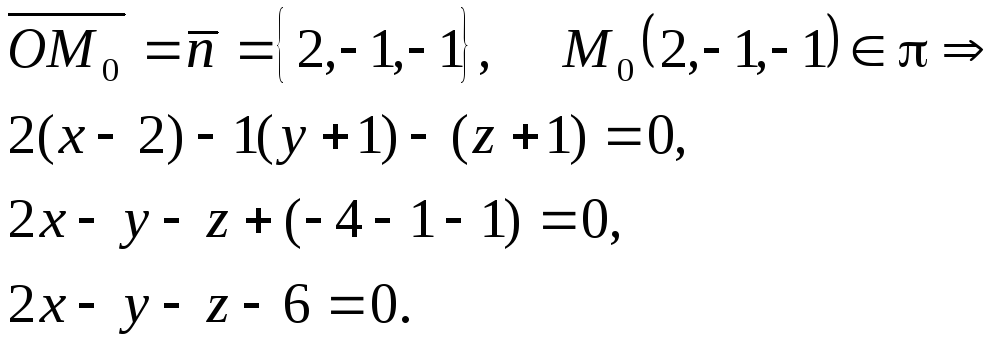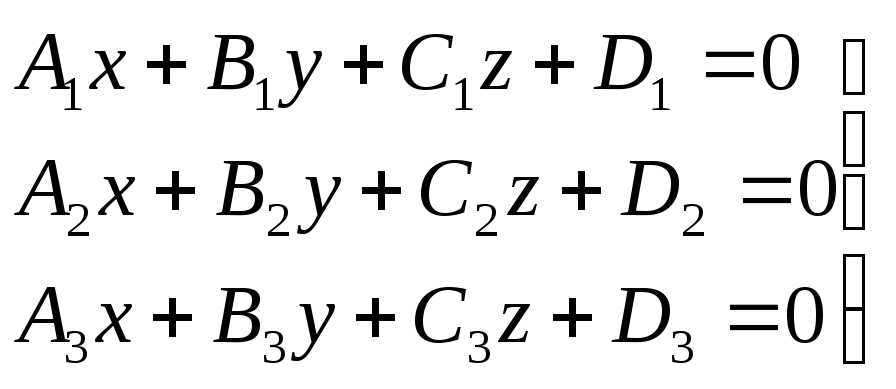Как найти нормаль плоскости через точку - Исправление недочетов и поиск решений вместе с Examum.ru

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

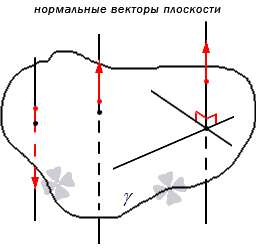
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через три точки

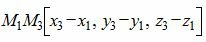
Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

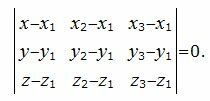(1)

Подставляя координаты точек A, B, C в (1), получим:

Разложим определитель по первому столбцу:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

Уравнение плоскости, проходящей через одну точку и имеющий нормаль n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

(2)

Подставляя координаты векторов M₀ и n в (2), получим:

Уравнение плоскости.

Общее уравнение плоскости

Любую плоскость можно задать уравнением плоскости первой степени вида

A x + B y + C z + D = 0

где A, B и C не могут быть одновременно равны нулю.

Уравнение плоскости в отрезках

Если плоскость пересекает оси OX, OY и OZ в точках с координатами ( a , 0, 0), (0, b , 0) и (0, 0, с ), то она может быть найдена, используя формулу уравнения плоскости в отрезках

x	+	y	+	z	= 1
a	b	c

Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали

Чтобы составить уравнение плоскости, зная координаты точки плоскости M( x ₀, y ₀, z ₀) и вектора нормали плоскости n = < A; B; C >можно использовать следующую формулу.

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле

x — x ₁	y — y ₁	z — z ₁	= 0
x ₂ — x ₁	y ₂ — y ₁	z ₂ — z ₁
x ₃ — x ₁	y ₃ — y ₁	z ₃ — z ₁

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

источники:

http://matworld.ru/analytic-geometry/uravnenie-ploskosti-online.php

http://ru.onlinemschool.com/math/library/analytic_geometry/plane/

Источник

Как найти нормаль плоскости

Нормаль плоскости n (вектор нормали к плоскости) – это любой направленный перпендикуляр к ней (ортогональный вектор). Дальнейшие выкладки по определении нормали зависят от способа задания плоскости.

Инструкция

Если задано общее уравнение плоскости — AX+BY+CZ+D=0 или его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то можно сразу записать ответ — n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.

Для получения общего ответа, вам понадобится векторное произведение векторов из-за того, что последнее всегда перпендикулярно исходным векторам. Итак, векторным произведением векторов, является некоторый вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом этот вектор (обозначьте его через n) ортогонален a и b – это главное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается против часовой стрелки.
[a,b] — одно из общепринятых обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, используется вектор-определитель (см. рис.1)

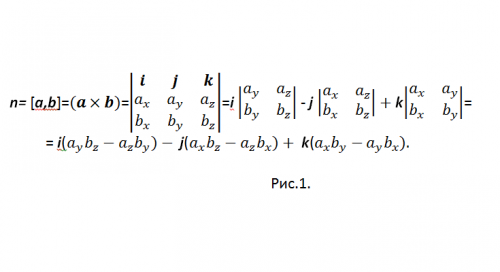
Для того чтобы не путаться со знаком «-», перепишите результат в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.
Более того, дабы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.

Вернитесь к решению поставленной задачи. Плоскость можно задать различными способами. Пусть нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно.
Пусть даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),
nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом,
nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль найдена — n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

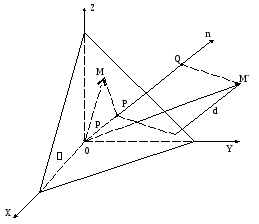
Нормальное уравнение плоскости. Расстояние от точки до плоскости.

Пусть
существует плоскость
.
Проведем нормальчерез начало координат О. Пусть заданы– углы, образованные нормальюс осями координат..
Пусть–
длина отрезка нормалидо пересечения с плоскостью. Считая
известными направляющие косинусы
нормали,
выведем уравнение плоскости.

Пусть
)
– произвольная точка плоскости. Вектор
единичной нормали имеет координаты.
Найдем проекцию вектора
на нормаль.

Поскольку
точка М
принадлежит плоскости, то

(8)

Это
и есть уравнение заданной плоскости,
называющееся нормальным.

Расстояние от точки до плоскости

Пусть
дана плоскость
,М*– точка пространства,d
– её расстояние
от плоскости.

Определение.
Отклонением
точки М*
от плоскости называется
число (+d),
если M*
лежит по ту сторону от плоскости, куда
указывает положительное направление
нормали
,
и число (-d),
если точка расположена по другую сторону
плоскости:

Теорема.
Пусть
плоскость
с единичной нормальюзадана нормальным уравнением:

Пусть
М*– точка пространства Отклонение т.M*
от плоскости задаётся выражением

. (9)

Доказательство.
Проекцию т.
*
на нормаль обозначимQ.
Отклонение точки М*
от плоскости равно

;

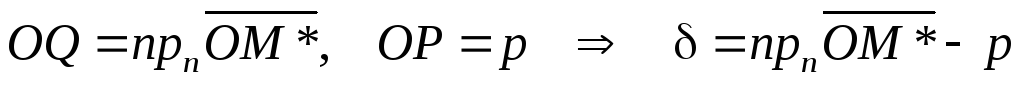
(9)

Правило.
Чтобы найти отклонение
т. M*
от плоскости, нужно в нормальное уравнение
плоскости подставить координаты т. M*.
Расстояние от точки до плоскости равно
.

Приведение общего уравнения плоскости к нормальному виду

Пусть
одна и та же плоскость задана двумя
уравнениями:

—
общее уравнение,

—
нормальное уравнение.

Поскольку оба
уравнения задают одну плоскость, их
коэффициенты пропорциональны:

Первые три равенства
возведем в квадрат и сложим:

Отсюда
найдем
– нормирующий множитель:

. (10)

Умножив
общее уравнение плоскости на нормирующий
множитель, получим нормальное уравнение
плоскости:

Примеры задач на тему «Плоскость».

Пример
1. Составить
уравнение плоскости
,
проходящей через заданную точку(2,1,-1)
и параллельной плоскости.

Решение.
Нормаль к плоскости
:.
Поскольку плоскости параллельны, то
нормальявляется и нормалью к искомой плоскости.
Используя уравнение плоскости, проходящей
через заданную точку (3), получим для
плоскостиуравнение:

Ответ:

Пример
2. Основанием
перпендикуляра, опущенного из начала
координат на плоскость
,
является точка.
Найти уравнение плоскости.

Решение.
Вектор
является нормалью к плоскости.
ТочкаМ₀
принадлежит плоскости. Можно воспользоваться
уравнением плоскости, проходящей через
заданную точку (3):

Ответ:

Пример
3. Построить
плоскость
,
проходящую через точкии перпендикулярную
плоскости
:.

Следовательно,
чтобы некоторая точка М
(x, y,
z)
принадлежала плоскости
,
необходимо, чтобы три векторабыли
компланарны:

=0.

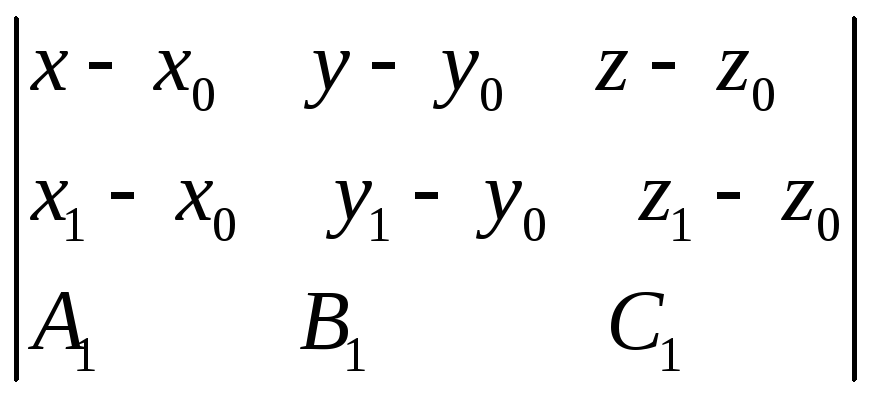
Осталось
раскрыть определитель и привести
полученное выражение к виду общего
уравнения (1).

Пример
4. Плоскость
задана
общим уравнением:

Найти
отклонение точки
от заданной плоскости.

Решение.
Приведем уравнение плоскости к нормальному
виду.

Подставим
в полученное нормальное уравнение
координаты точки М*.

Ответ:
.

Пример
5. Пересекает
ли плоскость
отрезок.

Решение.
Чтобы отрезок АВ
пересекал плоскость, отклонения
иот плоскостидолжны иметь разные знаки:

Пример
6. Пересечение
трех плоскостей в одной точке.

Система
имеет единственное решение, следовательно,
три плоскости имеют одну общую точку.

Пример
7. Нахождение
биссектрис двугранного угла, образованного
двумя заданными плоскостями.

Пусть
и— отклонение некоторой точкиот первой и второй плоскостей.

На одной из
биссектральных плоскостей (отвечающей
тому углу, в котором лежит начало
координат) эти отклонения равны по
модулю и знаку, а на другой – равны по
модулю и противоположны по знаку.

— это уравнение
первой биссектральной плоскости.

— это уравнение
второй биссектральной плоскости.

Пример
8. Определение
местоположения двух данных точек
иотносительно двугранных углов,
образованных данными плоскостями.

Пусть
.
Определить: в одном, в смежных или в
вертикальных углах находятся точкии.

Находим
и,и— это отклонения точекА
и В от
плоскостей
и.

а).
Если
илежат по одну сторону оти от,
то они лежат в одном двугранном углу.

б).
Если
илежат по одну сторону оти по разные от,
то они лежат в смежных углах.

в).
Если
илежат по разные стороны оти,
то они лежат в вертикальных углах.

Системы
координат 3

Линии
на плоскости 8

Линии
первого порядка. Прямые на плоскости. 10

Угол
между прямыми 12

Общее
уравнение прямой 13

Неполное
уравнение первой степени 14

Уравнение
прямой “в отрезках” 14

Совместное
исследование уравнений двух прямых 15

Нормаль
к прямой 15

Угол
между двумя прямыми 16

Каноническое
уравнение прямой 16

Параметрические
уравнения прямой 17

Нормальное
(нормированное) уравнение прямой 18

Расстояние
от точки до прямой 19

Уравнение
пучка прямых 20

Примеры
задач на тему «прямая на плоскости» 22

Векторное
произведение векторов 24

Свойства
векторного произведения 24

Геометрические
свойства 24

Алгебраические
свойства 25

Выражение
векторного произведения через координаты
сомножителей 26

Смешанное
произведение трёх векторов 28

Геометрический
смысл смешанного произведения 28

Выражение
смешанного произведения через координаты
векторов 29

Примеры
решения задач по теме: «Векторная
алгебра». 30

Поверхности
в пространстве 33

Плоскость 33

Неполные
уравнения плоскости 35

Уравнение
плоскости в «отрезках» 35

Угол
между плоскостями 36

Уравнение
плоскости, проходящей через три точки,
не принадлежащие одной прямой 37

Нормальное
уравнение плоскости. Расстояние от
точки до плоскости. 38

Расстояние
от точки до плоскости 39

Приведение
общего уравнения плоскости к нормальному
виду 40

Примеры
задач на тему «Плоскость». 40

Линии
в пространстве. Прямая в пространстве 46

Канонические
уравнения прямой в пространстве 47

Параметрические
уравнения прямой 48

Уравнения
прямой, проходящей через две заданные
точки 48

Угол
между двумя прямыми в пространстве 49

Угол
между прямой и плоскостью 49

Условие
принадлежности двух прямых одной
плоскости 50

Некоторые
задачи на построение прямых и плоскостей 50

Примеры
решения задач по теме «Аналитическая
геометрия» 55

Кривые
второго порядка 59

Пример
приведения общего уравнения линии
второго порядка к каноническому виду 59

Эллипс 62

Вывод
уравнения эллипса 62

Гипербола 64

Парабола 65

Примеры
решения задач на тему «Кривые второго
порядка». 66

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Если Ваш репетитор по математике имеет высокую квалификацию, то он должен это знать. В противном случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ по математике С1-С6 обычно включает разбор основных алгоритмов и формул, описанных ниже.

Угол между прямыми а и b

Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 180 град).

Какой алгоритм использует репетитор по математике для поиска угла?

1) Выбираем любые вектора и , имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов $overrightarrow{AB}(x_1;y_1)$ и $overrightarrow{CD}(x_2;y_2)$ по соответствующим координатам их начал и концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденный координаты в формулу:
$Cos (widehat{AB,CD}) =left vert Cos(widehat{ overrightarrow{AB},overrightarrow{CD}}) right vert =left vert dfrac{x_1x_2+y_1y_2}{sqrt{x_1^2+y_1^2} cdot sqrt{x_2^2+y_2^2}} right vert$ . Для нахождения самого угла, нужно найти арккосинус полученного результата.

Нормаль к плоскости

Нормалью vec{n} к плоскости называется любой вектор, перпендикулярный к этой плоскости.
Как найти нормаль? Для поиска координат нормали достаточно узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По этим координатам находим координаты векторов и и требуем выполнения условий и . Приравнивая скалярные произведение векторов к нулю, составляем систему уравнений с тремя переменными, из которой можно найти координаты нормали.

Замечание репетитора по математике: Совсем не обязательно решать систему полностью, ибо достаточно подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь из ее неизвестных координат любое число (например единицу) и решить систему двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то это значит, что в семействе нормалей нет той, у которой по выбранной переменной стоит единица. Тогда подставьте единицу вместо другой переменной (другой координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль будет иметь единицу по последней координате, а сама она окажется параллельной какой-нибудь координатной плоскости (в таком случае ее легко найти и без системы).

Угол между прямой и плоскостью

Допустим, что нам заданы прямая и плоскость координатами направляющего вектора $overrightarrow{AB}(x_1;y_1)$ и нормали $overrightarrow{n}(x_2;y_2)$
Угол psi между прямой и плоскость вычисляется по следующей формуле:
$Sin psi = left vert Cos(widehat{ overrightarrow{n},overrightarrow{AB}}) right vert = left vert dfrac{x_1x_2+y_1y_2}{sqrt{x_1^2+y_1^2} cdot sqrt{x_2^2+y_2^2}} right vert$

Угол между плоскостями

Пусть $overrightarrow{n_1} (x_1;y_1)$ и $overrightarrow{n_1} (x_1;y_1)$ — две любые нормали к данным плоскостям. Тогда косинус угла между плоскостями равен модулю косинуса угла между нормалями:

$Cos psi = left vert Cos(widehat{ overrightarrow{n_1},overrightarrow{n_2}}) right vert =left vert dfrac{x_1x_2+y_1y_2}{sqrt{x_1^2+y_1^2} cdot sqrt{x_2^2+y_2^2}} right vert$

Уравнение плоскости в пространстве

Точки, удовлетворяющие равенству образуют плоскость с нормалью . Коэффициент отвечает за величину отклонения (параллельного сдвига) между двумя плоскостями с одной и той же заданной нормалью . Для того, чтобы написать уравнение плоскости нужно сначала найти ее нормаль (как это описано выше), а затем подставить координаты любой точки плоскости вместе с координатами найденной нормали в уравнение и найти коэффициент .

Расстояние от точки до плоскости

Для вычисления расстояния от точки до плоскости alpha , заданной уравнением можно использовать следующую формулу:

$rho(M;alpha)=dfrac{|A cdot x_0 + B cdot y_0 + C cdot z_0 + D|}{sqrt{A^2+B^2+C^2}}$
В знаменателе стоит длина нормали, а числителе — значение выражения из левой части уравнения плоскости в точке

Комментарий репетитора по математике:

Методом координат можно находить не только углы и расстояния в пространстве, но и
1) площади многоугольников (треугольника, параллелограмма), расположенных в заданной плоскости.
2) объемы простейших многогранников (параллелепипедов и пирамид).

Для понимания таких формул нужно изучить понятия векторного и смешанного произведения векторов, а также определителя матрицы. В скором времени я сделаю для вычисления объемов соответствующую справочную страничку.

Средства аналитической геометрии репетитор по математике практически не использует в работе со средним и тем более слабым учеником. И очень жаль, что загруженность среднестатистического сильного школьника не позволяет репетитору провести более-менее серьезную работу на уровне определений из высшей математики и с соответствующей практикой решения задач. Поэтому я часто ограничиваюсь простым сообщением формул и демонстрацией одного – двух примеров их использования. В школьной программе не предусмотрено время для изучения векторных приемов вообще, однако на ЕГЭ Вы имеете право решать задачу С2 любым из известных науке способов. Отсюда мораль: учите координаты. Расширенная подготовка к ЕГЭ по математике с изучением приемов аналитической геометрии даст Вам мощное и универсальное средство для решения огромного класса задач типа С2. Пользуйтесь этой страничкой на здоровье!

Колпаков А.Н. Репетитор по математике Москва (Строгино).

Источник

Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.

Общее уравнение плоскости принимает вид:

Общее уравнение плоскости

Ax+By+Cz+D=0Ax+By+Cz+D=0,

где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.

Здесь будет калькулятор

Составление уравнения плоскости по трем точкам

Текст цитаты

Заголовок

Текст цитаты

В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:

Уравнение плоскости через определитель

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,

где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.

Задача 1

Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).

Решение

Пусть:

x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0

Составляем определитель:

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0

∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0

∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0

28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.

Ответ

28x−8y−22z−4=028x-8y-22z-4=0

Уравнение плоскости по точке и вектору нормали

Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:

Уравнение плоскости по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.

Задача 2

Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).

Решение

x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0

(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0

x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0

x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.

Проверка

Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:

8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0

0=00=0 — верно, значит ответ правильный.

Ответ

x+3y+5z−47=0x+3y+5z-47=0

Источник