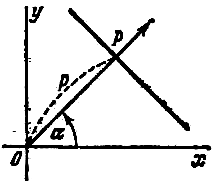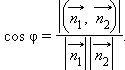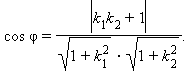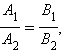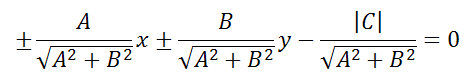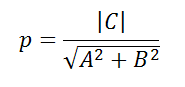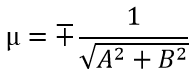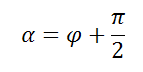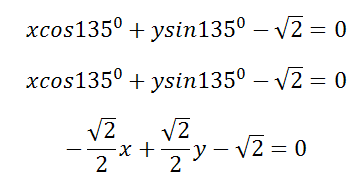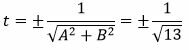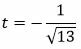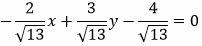Нормальное уравнение прямой
В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
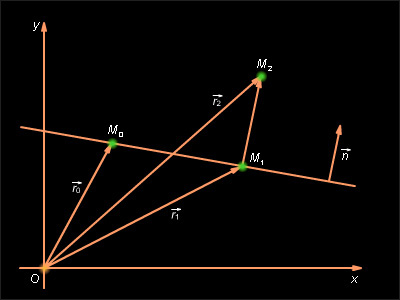
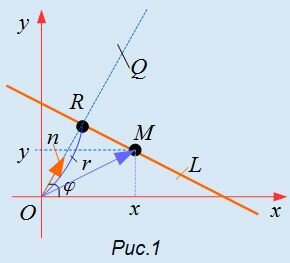
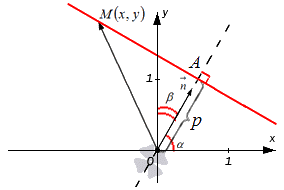
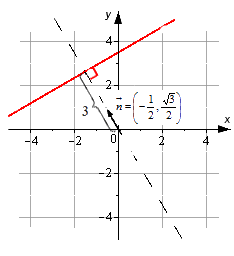
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 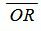
Выразим уравнение прямой L через два параметра: длину отрезка 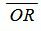
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
Скалярное произведение векторов n и 
где 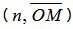


Поскольку n единичный вектор, то (4) можно записать так:
Учитывая, что n={cosφ, sinφ}, 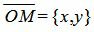
Тогда из уравнений (3), (5), (6) следует:
или
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой.
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
Подставляя вычисленные значения в (7) получим:
Ответ:
Приведение общего уравнения прямой на плоскости к нормальному виду
Пусть на плоскости задано уравнение прямой в общем виде:
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
Упростим выражение и найдем t:
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем.
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
Так как C>0, то знак t отрицательный:
Умножим уравнение (12) на t:
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
Отметим, что число 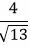
Пусть
на плоскости хОу дана прямая. Проведем
через начало координат перпендикуляр
к данной прямой и назовем его нормалью.
Обозначим через Р точку пересечения
нормали с данной прямой и установим
положительное направление нормали от
точки О к точке Р.
Если
—
полярный угол нормали, р — длина отрезка
(рис.),
то уравнение данной прямой может быть
записано в виде
;
уравнение
этого вида называется нормальным.
Пусть
дана какая-нибудь прямая и произвольная
точка
;
обозначим через d
расстояние от точки М* до данной прямой.
Отклонением
точки
от
прямой называется число +d,
если данная точка и начало координат
лежат по разные стороны от данной прямой,
и -d,
если данная точка и начало координат
расположены по одну сторону от данной
прямой. (Для точек, лежащих на самой
прямой,
=0).
Если даны координаты
,
точки
и
нормальное уравнение прямой
,
то отклонение
точки
от
этой прямой может быть вычислено по
формуле
.
Таким
образом, чтобы найти отклонение
какой-нибудь точки
от
данной прямой, нужно в левую часть
нормального уравнения этой прямой
вместо текущих координат подставить
координаты точки
.
Полученное число будет равно искомому
отклонению.
Чтобы
найти расстояние d
от точки до прямой, достаточно вычислить
отклонение и взять его модуль:
.
Если
дано общее уравнение прямой
,
то, чтобы привести его к нормальному
виду, нужно все члены этого уравнения
умножить на нормирующий множитель
,
определяемый формулой
.
Знак
нормирующего множителя выбирается
противоположным знаку свободного члена
нормируемого уравнения.
12 Вычисление угла между прямыми
Пусть
прямые
и
заданы
общими уравнениями
|
|
Обозначим
через φ величину угла между прямыми
и
(напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами
и
этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство
Из
теоремы
11.10 следует, что
|
|
и,
следовательно,
|
|
Записав
через координаты, получим
|
|
Если
прямые
и
заданы
уравнениями с угловыми коэффициентами
и
|
|
то
нормальные векторы этих прямых могут
быть
и
выражение для косинуса угла между этими
прямыми будет иметь вид:
|
|
Из
последнего выражения следует, что если
то
cos φ = 1 и φ = 0, то есть прямые
параллельны или совпадают. С другой
стороны, если прямые параллельны, то
φ = 0 или cos φ = 1. Подставляя
в правую часть вместо cos φ его значение
1, умножая обе части на знаменатель и
возводя в квадрат, получим
|
|
Отсюда
получаем
Если
то
cos φ = 0 и
то
есть прямые перпендикулярны. Обратно,
если прямые перпендикулярны, то
или
cos φ = 0. Отсюда следует с
необходимостью
Следовательно,
необходимые и достаточные условия
параллельности и перпендикулярности
двух прямых, заданных уравнениями с
угловыми коэффициентами
и
формулируются
следующим образом.
Т
еорема 11.13.
Для
того чтобы прямые
и
были
-
параллельны,
необходимо и достаточно, чтобы -
перпендикулярны,
необходимо и достаточно, чтобы
Пользуясь
знанием координат направляющего и
нормального векторов прямых, заданных
общими уравнениями, можно сформулировать
условия параллельности и перпендикулярности
прямых через коэффициенты общих уравнений
этих прямых.
Т
еорема 11.14.
Для
того чтобы прямые
и
были
-
параллельны,
необходимо и достаточно, чтобы
соответствующие коэффициенты их
уравнений при одноименных неизвестных
были пропорциональны, то есть
-
перпендикулярны,
необходимо и достаточно, чтобы выполнялось
равенство
Доказательство
|
Пусть
задана прямая l
общим уравнением Ax + By + C = 0
и некоторая точка
лежащая
вне прямой. Поставим задачу найти
расстояние
от
этой точки до прямой l.
Опустим перпендикуляр
из
точки
на
прямую l
и обозначим
радиус-векторы
точек
и
соответственно
(см. рис. 11.6.1). Очевидно,
|
1 |
|
Рисунок |
Пусть
–
некоторая точка прямой l,
отличная от точки
Тогда
уравнение прямой l
можно записать в нормальной векторной
форме:
|
|
где
а
–
вектор нормали к прямой l.
Или, в векторной форме,
Очевидно,
справедливо векторное равенство
причем
поэтому
Умножив
обе части равенства скалярно на вектор
, получим
|
|
Так
как точка
лежит
на прямой l,
то
и,
следовательно,
Подставляя
в исходное равенство, найдем
|
|
Отсюда
|
|
Переходя
к координатной форме записи и учитывая,
что
имеем
|
|
Таким
образом верна теорема
Т
еорема 11.15.
Растояние
от
точки
до
прямой l,
заданной уравнением Ax + By + C = 0
вычисляется по формуле
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как привести уравнение прямой к нормальному виду
Для того, чтобы найти нормальное уравнение прямой, заданной уравнением Ax+By+C=0, необходимо разделить данное уравнение на
при этом знак «минус» берётся, когда C>0, а знак «плюс» берётся, когда C<0. Если C=0, то можно взять любой знак. Тогда получим уравнение вида:
Если учесть, что полярное расстояние определяется по формуле,
а полярный угол по формулам
Тогда уравнение примет вид
x cosα + y sinα − p = 0
Это и есть нормальное уравнение прямой
То же самое получим, если обе части уравнения Ах + By + С = 0 умножим на число
то есть:
x cosα + y sinα − p = 0
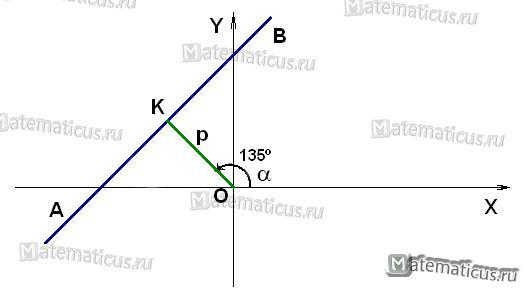
Графически это можно представить следующем образом
Прямая AB с полярным расстоянием p (длина перпендикуляра, опущенного на прямую из начала координат OK) и полярным углом α (угол измеренный в положительном направлении между положительным направлением оси Ox и направлением этого перпендикуляра) представляется уравнением:
x cosα + y sinα − p = 0
Если p=0, то прямая проходит через начало координат, а угол
задаёт угол наклона прямой.
Пример 1
Привести уравнение 3x-4y+5=0 к нормальному виду. Здесь A=3, B=-4, C=5>0. Поэтому делим на
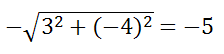
$ — frac{3}{5}x + frac{4}{5}x — 1 = 0$
Это уравнение вида
x cosα + y sinα − p = 0
здесь
p=1, $cos alpha = — frac{3}{5}$, $sin alpha = frac{4}{5}$
Пример 2
Пусть прямая AB стоит от начала оси координат на расстоянии OK=$sqrt 2 $ и пусть луч OK составляет с лучом OX угол равный α=1350
тогда нормальное уравнение прямой AB будет
Если умножить полученное уравнение на $-sqrt 2 $, получим уравнение прямой AB в виде
x-y+2 = 0, но это уравнение не является нормальным уравнением прямой.
2724
3. Полярные параметры прямой. Нормальное уравнение прямой. Преобразование координат
Полярными параметрами прямой L будут полярное расстояние р (длина перпендикуляра, проведенного к данной прямой из начала координат) и полярный угол α (угол между осью абсцисс ОХ и перпендикуляром, опущенным из начала координат на данную прямую L). Для прямой, представленной уравнением Ах + Ву + С = 0: полярное расстояние
полярный угол α
причем при C > 0 берется верхний знак, при C < 0 — нижний знак, при С = 0 знаки берутся произвольно, но либо оба плюса, либо оба минуса.
Нормальное уравнение прямой (уравнение в полярных параметрах) (cм. рис. 2): x cosα + y sinα — p = 0. Пусть прямая представлена уравнением вида Ах + Ву + С = 0. Чтобы данное уравнение привести к нормальному виду необходимо последнее разделить на выражение 
Рис. 2
После деления получается нормальное уравнение данной прямой:
Пусть имеется прямая L, которая пересекает оси координат. Тогда данная прямая может быть представлена уравнением в отрезках х / а + у / b = 1. Справедливо: если прямая представлена уравнением х / а + у / b = 1, то она отсекает на осях отрезки а, b.
Преобразование координат возможно путем переноса начала координат, или поворотом осей координат, или совместно переносом начала и поворотом осей.
При переносе начала координат справедливо следующее правило: старая координата точки равна новой, сложенной с координатой нового начала в старой системе. Например, если старые координаты точки М были х, у, а координаты нового начала в старой системе О*(х0, у0), то координаты точки М в новой системе координат с началом в точке О* будут равны х — х0, у — у0 т. е. справедливо следующее х = х* + х0, у = у* + у0 или х* = х — х0, у* = у — у0 (* новые координаты точки).
При повороте осей на некоторый угол φ справедливы следующие формулы (где х, у — старые координаты точки; х*, у* — новые координаты этой же точки):
x = x* cosα — y* sinα;
y = x* sinα + y* cosα
или
x* = x cosα + y sinα;
y* = — x sinα + y cosα.
Нормальное уравнение прямой
В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 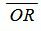
Выразим уравнение прямой L через два параметра: длину отрезка 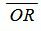
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
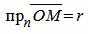 |
(3) |
Скалярное произведение векторов n и 
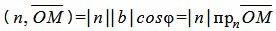 , , |
(4) |
где 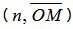


Поскольку n единичный вектор, то (4) можно записать так:
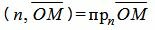 . . |
(5) |
Учитывая, что n=<cosφ, sinφ>, 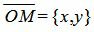
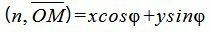 . . |
(6) |
Тогда из уравнений (3), (5), (6) следует:
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой .
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
Подставляя вычисленные значения в (7) получим:
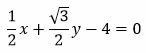
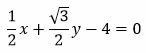
Приведение общего уравнения прямой на плоскости к нормальному виду
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что
| tAx=cosφ, tB=sinφ, tC=−r. | (9) |
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 =cos 2 φ+sin 2 φ=1. | (10) |
Упростим выражение и найдем t:
t 2 A 2 +t 2 B 2 =t 2 (A 2 +B 2 )=1,
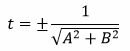 . . |
(11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
Так как C>0, то знак t отрицательный:
Умножим уравнение (12) на t:
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
Отметим, что число 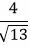
Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnoe-normirovannoe-uravnenie-prjamoj/
http://vmath.ru/vf5/diffgeom/seminar1