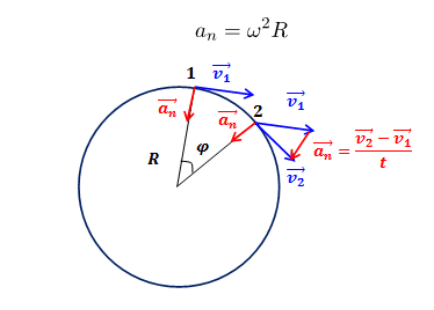
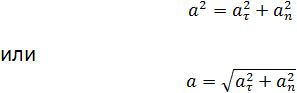Касательное и нормальное ускорения точки
Касательное ускорение характеризует изменение в данное мгновение вектора скорости по величине, а нормальное — по направлению
Проекция ускорения на касательную и на нормаль
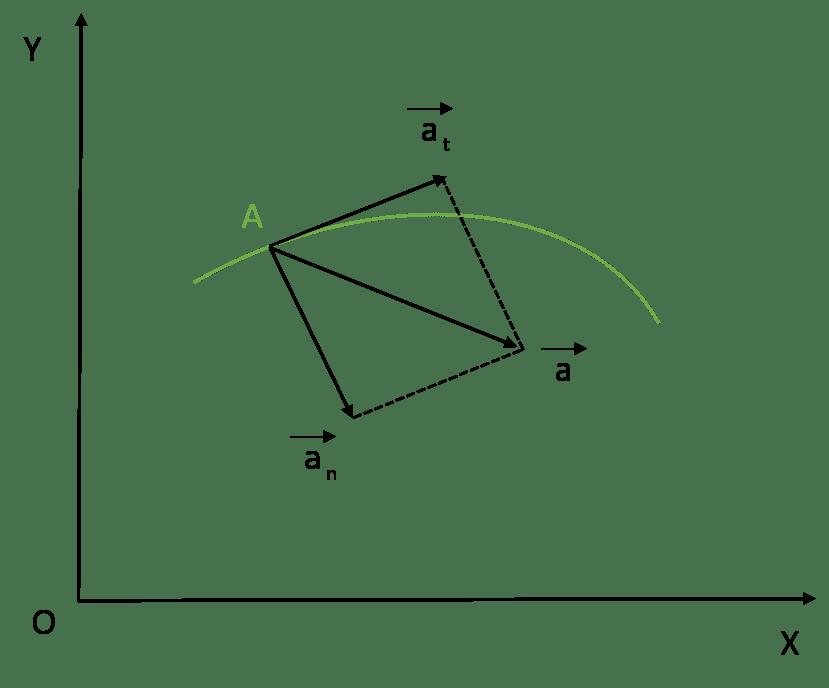
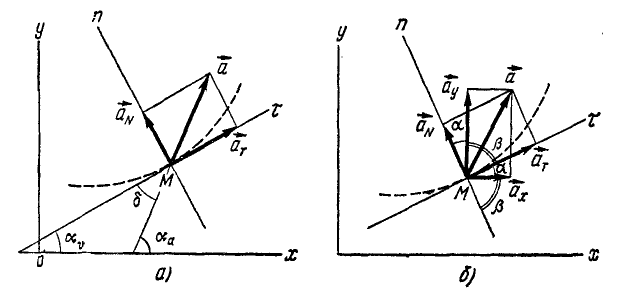
Если движение точки задано в векторной или в координатной форме, то часто встречается необходимость определить проекции ускорения на касательную и главную нормаль к траектории точки в том ‘ месте, где в данное мгновение находится точка (рис. 91, а).
При естественной форме определения движения точки сначала определяют проекции ускорения на касательную и на нормаль, а затем уже по этим проекциям находят величину и направление полного ускорения точки.
Проекцию ускорения точки на касательную к ее траектории называют касательным ускорением, или тангенциальным ускорением (от латинского слова tangens—касающийся), и обозначают aN.
Проекцию ускорения на нормаль называют нормальным ускорением и обозначают ar.
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины. В таком случае над аr и aN ставят стрелку, указывающую на их векторный характер.
Разложение ускорения по касательной и нормали имеет физический смысл: касательная составляющая ускорения направлена по касательной (как и скорость), а потому не может повлиять на направление скорости, но влияет на ее величину; составляющая ускорения по нормали направлена перпендикулярно к скорости, а потому не может повлиять на величину скорости, но влияет на ее направление.
Касательное ускорение равно первой производной от величины скорости по времени:
Касательное ускорение
Пусть точка M движется по траектории, расположенной в плоскости хОу.
Проведем касательную и нормаль к кривой в точке M (рис. 91, б), нанесем на чертеж вектор ускорения 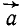
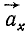
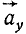
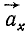
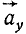
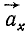
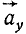
Составляющие ускорения 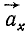
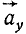
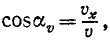
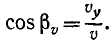
Подставляя значения направляющих косинусов, получаем
По формуле (68) удобно вычислять касательное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).
Можно дать еще другой изящный вывод формулы (68) тангенциального ускорения, для чего спроецировать на касательную вектор полного ускорения, не раскладывая его предварительно по осям декартовых координат. В самом деле, тангенциальное ускорение равно проекции полного ускорения на касательную (рис. 91, а):
ar = a cos δ,
но угол δ, как внутренний угол треугольника, равен внешнему αа без другого внутреннего αυ, поэтому:
cos δ = cos (αа—aυ) = cos αа cos aυ + sin αа sin aυ
или, так как αа = 90°- βa и aυ = 90°-βυ,
cos δ = cos αа cos aυ + cos βa cos βυ .
Подставляя сюда вместо направляющих косинусов их выражения (67) n (62′), получим
Напомним, что в числителе этой формулы проекции имеют свой знак, а знаменатель определяется по (64), т. е. существенно положителен.
Задача №1
Движение точки задано в декартовых координатах уравнениями:
x=21,2 sin2 t, y=21,2 cos2 t
Определить касательное ускорение точки (см. задачу № 36, стр. 132).
Решение. Дифференцируя уравнения движения, найдем υx = 21,2 sin 2t, υy = -21,2 sin 2t. Определим теперь полную скорость:
Дифференцируя уравнения движения вторично, найдем
αx = 42,2 cos 2t, αy = -42,4 cos 2t.
Касательное ускорение определим по формуле (68):
Ответ. Касательное ускорение равно 60 cos 2t.
Задача №2
Точка M движется в системе координат хОу согласно уравнениям x=r cos πt, y=r sin πt. Найти касательное ускорение точки М.
Решение. Проекции скорости и ускорения на оси координат, а также и полная скорость точки M были уже нами получены при решении задачи № 44 (см. стр. 142). Для определения касательного ускорения точки M нам остается только подставить эти величины в формулу (68):
Ответ. Касательное ускорение равняется нулю.
Для случая задания движения в естественной форме преобразуем формулу (68) следующим образом:
и, сокращая на υ, найдем касательное ускорение
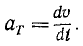
Принимая во внимание (53), можно придать этой формуле несколько иной вид:
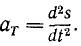
Итак, касательное ускорение—это проекция ускорения точки на касательную к траектории, равная первой производной от величины скорости по времени. Чтобы получить касательное ускорение в векторном выражении, нужно его умножить на единичный вектор касательной:
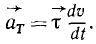
Как уже было сказано, касательное ускорение не может изменить направления скорости, оно характеризует быстроту изменения величины скорости, т. е. соответствует изменению вектора скорости вдоль его направления.
Если с течением времени величина скорости увеличивается, то касательное ускорение направлено в ту же сторону, что и скорость. Такое движение называют ускоренным.
Если же величина скорости уменьшается, то касательное ускорение направлено в сторону, противоположную скорости. Такое движение называют замедленным.
Каждое из этих движений называют переменным движением.
Если величина скорости точки постоянна, то производная 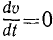
Обратное заключение можно сделать лишь с некоторой оговоркой: если касательное ускорение постоянно равняется нулю, то, следовательно, величина скорости постоянна и движение равномерно; если же касательное ускорение точки равняется нулю не в течение всего рассматриваемого промежутка времени, а только в какое-то мгновение, то движение точки не является равномерным, и равенство 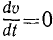
При равномерном движении точки по любой траектории
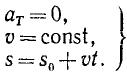
Формулы (70) справедливы только для равномерного движения точки и неприменимы при других движениях.
Равнопеременное движение точки
Из переменных движений точки в задачах наиболее часто встречается равнопеременное движение — такое движение, при котором касательное ускорение остается постоянным.
При равнопеременном движении точки по любой траектории
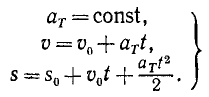
Формулы (71) справедливы только для равнопеременного движения и неприменимы при других движениях. Они даны здесь без вывода и известны из элементарной физики. Вывод этих формул приведен в решении задачи № 48.
Задача №3
Точка А начала двигаться с начальной скоростью υ0= 1 м/сек и с ускорением aT =2 м/сек2. Через одну секунду следом за точкой А по той же траектории с такой же начальной скоростью и с таким же касательным ускорением стала двигаться точка В. Определить расстояние (по траектории) между точками А и В через t сек после выхода первой точки. Построить графики движения точек.
Решение. Определим сначала уравнение движения точек. Нам дано, что
Разделяя переменные и интегрируя, получим
υ = aTt + C1
Постоянную C1 определим из начальных данных:
υ0 = aT . 0 + C1; C1=υ0
Следовательно,
υ = υ0 + aTt.
Написав υ по (53), разделяя переменные и интегрируя, найдем
где
С2 = s0 = 0.
Подставляя вместо υ0 и аT заданные величины, найдем расстояние (в м), пройденное точкой А за время t:
В то же мгновение t расстояние, пройденное точкой В, будет меньше, так как точка В будет находиться в пути лишь t—1 сек. Для точки В
Расстояние между A и B найдем как разность пройденных ими путей:
Это расстояние растет пропорционально времени, хотя точка В во времени не отстает от точки А и каждую точку траектории проходит через 1 сек после того, как через нее прошла точка А.
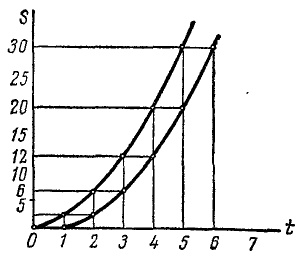
Графики движения точек А и В изображаются одинаковыми параболами (рис. 92), но парабола, представляющая движение точки В, смещена по оси времени относительно параболы, представляющей движение точки А, на 1 сек вправо. Чтобы определить расстояние (в м) между А и В в какое-либо мгновение, надо восставить перпендикуляр к оси времени в точке, соответствующей этому мгновению, и измерить расстояние по вертикали между параболами. Чтобы определить интервал времени (в сек) между прохождениями точками А и В какой-либо точки К траектории, надо восставить перпендикуляр к оси расстояний в точке, соответствующей расстоянию точки К от начала отсчета, и измерить расстояние по горизонтали между параболами. Графики наглядно показывают, что точка В отстает от точки А по расстоянию, так как А В непрерывно увеличивается, но не отстает по времени, и точка В проходит каждый отрезок траектории за такое же время, как и точка А.
Рис. 92
Ответ. SA— SB = 2t м.
Нормальное ускорение равно отношению квадрата скорости точки к радиусу кривизны траектории:
Нормальное ускорение
Чтобы получить формулы нормального ускорения, мы опять воспользуемся тем, что проекция вектора на ось равна сумме проекций его составляющих на ту же ось, и определим aN как алгебраическую сумму проекций составляющих ax и ay на нормаль к траектории точки. Выберем за положительное направление нормали то, которое получается от поворота положительного направления касательной на прямой угол против хода часов (см. рис. 91) в сторону вогнутости кривой.
Как видно из чертежа (см. рис. 91, б)
aN = ay cos αυ—ax cos βυ.
Подставляем значения (62) направляющих косинусов:
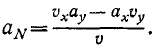
По этой формуле удобно вычислять нормальное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).
Эту же формулу (72) можно получить, спроецировав полное ускорение а на нормаль Mn (рис. 91, а):
aN = a sin δ = a sin (αα—αυ)
или
aN=a (sinαα cos αυ -cos αα sin αυ).
Подставляя эти значения и сокращая на а, получим:
Задача №4
Движение точки задано уравнениями X= 21,2 sin2 t, у= 212 cos2 t. Определить нормальное ускорение точки.
Решение. Дифференцируя эти же уравнения движения при решении задачи № 36 (см. стр. 132), мы уже определили нужные нам величины: υx, υy, υ, ax, ау. Подставляя их в формулу (72), найдем
Ответ. Нормальное ускорение равно нулю.
Задача №5
Точка M движется согласно уравнениям x= r cos πt, y= r sin πt. Найти нормальное ускорение точки М.
Решение. Дифференцируя при решении задачи № 44 (см. стр. 142) эти уравнения движения, мы уже нашли проекции скорости и проекции ускорения. Полную скорость определим по ее проекциям согласно (64):
Подставляя все эти величины в формулу (72), найдем
Ответ. Нормальное ускорение равно rπ2.
Чтобы преобразовать формулу (72) для случая, когда движение точки задано в естественной форме, припомним из курса высшей математики выражение кривизны плоской кривой, представленной в параметрической форме уравнениями (58′) и (58″),
Если параметр t означает время, то эту геометрическую формулу можно переписать в обозначениях кинематики:
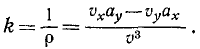
Сравнивая равенства (72) и (73), находим
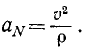
Мы получили положительное значение проекции, следовательно, нормальное ускорение направлено от точки M в положительном направлении оси Mn (см. рис. 91), т. е. в ту сторону от касательной, по которую лежит траектория точки.
Чтобы получить нормальное ускорение в векторном выражении, надо (74) умножить на единичный вектор 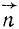
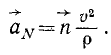
Как уже было сказано, нормальное ускорение не влияет на величину скорости, потому что оно направлено перпендикулярно к скорости. Оно влияет на направление скорости.
Итак, нормальное ускорение—это проекция ускорения точки на нормаль к траектории, направленная в сторону вогнутости, равная квадрату скорости, деленному на радиус кривизны траектории.
Если движение точки прямолинейное, то радиус кривизны траектории (прямой линии) равен бесконечности, а нормальное ускорение равно нулю.
Обратное заключение можно сделать лишь с некоторой оговоркой: если в каждое мгновение данного промежутка времени нормальное ускорение движущейся точки равняется нулю, то точка движется по прямой; если же нормальное ускорение точки не постоянно равно нулю, а только в какое-либо мгновение, то движение точки не а потому
является прямолинейным и равенство 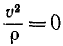
Рис. 93
Величина ускорения точки равна квадратному корню из суммы квадратов касательного и нормального ускорений:
Ускорение при естественном способе задания движения
Если движение точки задано в естественной форме, то проекции ускорения на нормаль и на касательную можно определить по формулам (69) и (74) и по проекциям определить величину полного ускорения точки (см. рис. 91):
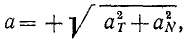
или
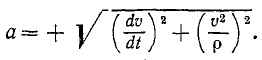
Перед радикалом стоит знак « + », потому что величина ускорения существенно положительна.
Вектор полного ускорения 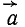
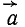
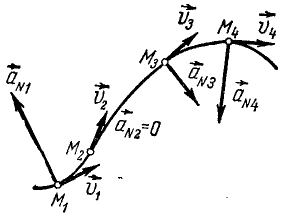
Касательное ускорение направлено по касательной к траектории, а нормальное к центру кривизны траектории, поэтому вектор полного ускорения лежит с той стороны от касательной, с которой расположена траектория точки.
При криволинейном ускоренном движений точки полное ускорение составляет со скоростью острый угол, а при замедленном—тупой.
Вектор ускорения лежит в соприкасающейся плоскости, и проекция ускорения на бинормаль равна нулю:
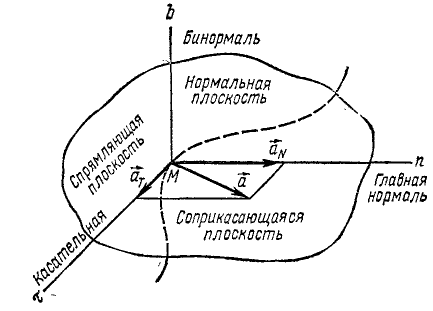
Разложение ускорения при движении точки по кривой двоякой кривизны. Если кривая не лежит в одной плоскости, то ее называют пространственной кривой, или кривой двоякой кривизны. В каждой точке к кривой можно провести только одну касательную и бесчисленное множество нормалей, расположенных в плоскости, перпендикулярной к касательной и называемой нормальной плоскостью (рис. 94).
рис. 94
Пусть в мгновение t точка занимает на кривой двоякой кривизны положение М. В это мгновение скорость точки направлена по касательной к кривой в точке М. Через эту касательную и через близкую точку M1 (не показанную на чертеже)., в которую движущаяся точка придет в мгновение t + Δt, проведем плоскость и будем стремить Δt к нулю. Тогда точка M1 будет стремиться к точке М. При этом плоскость будет поворачиваться около касательной, проведенной в точке М и стремиться к некоторому определенному положению, в котором она называется соприкасающейся плоскостью. Следовательно, в соприкасающейся плоскости находится вектор скорости движущейся точки в то мгновение, когда эта точка совпадает с точкой М, а также когда она занимает положение, предельно близкое к точке M. А так как ускорение характеризует изменение скорости в данное мгновение, то вектор ускорения тоже находится в соприкасающейся плоскости.
Плоскость, проведенную через точку M перпендикулярно к соприкасающейся и к нормальной плоскостям, называют спрямляющей плоскостью.
Нормаль, лежащую в спрямляющей плоскости, называют бинормалью, а нормаль, лежащую в соприкасающейся плоскости,—главной нормалью (главную нормаль плоской кривой обычно называют просто нормалью).
Касательная Mτ главная нормаль Mn и бинормаль Mb пересекаются в точке M под прямыми углами. Эти три взаимно перпендикулярные прямые в механике часто принимают в качестве координатных осей и называют естественными осями, или осями натурального триэдра. По мере движения точки по траектории естественные оси движутся вместе с ней, поворачиваются относительно основных (неподвижных) осей xOyz.
Положительные направления на естественных осях примем такими, чтобы трехгранный угол τMnb можно было привести в совпадение с углом xОyz. Касательная Mτ играет роль оси Ох, главная нормаль Mn— оси Oy и бинормаль Mb— оси Oz.
Так как вектор ускорения лежит в соприкасающейся плоскости τМn, а бинормаль Mb перпендикулярна к соприкасающейся плоскости, то проекция ускорения на бинормаль всегда равна нулю (αb = 0), и при проецировании ускорения на три естественные оси мы имеем только две проекции: касательное ускорение и нормальное ускорение.
Таким образом, мы установили, что формулы (69), (69′) и (69″) касательного ускорения, формулы (74) и (74′) нормального ускорения, а также формулы (75) и (75′) полного ускорения, выведенные нами в предположении, что точка движется по плоской траектории, остаются справедливыми для любого движения точки.
Именно потому, что проекция ускорения на бинормаль всегда равна нулю, в формуле (75) величина полного ускорения определяется по двум проекциям, а не по трем, как это имеет место в формуле (66). Приравнивая выражение (66) модуля полного ускорения точки через проекции на неподвижные оси координат его же выражению (75) через проекции на естественные оси, получим для движения точки по любой траектории соотношение
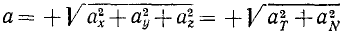
или
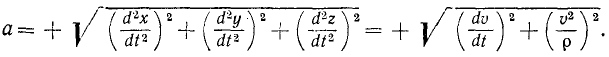
Эти равенства часто бывают полезны при решении задач.
Задача №6
Найти касательное и нормальное ускорения точки, движение которой выражается уравнениями:
Решение. Найдем проекции скорости и ускорения на оси координат:
x=υx=α, χ=ax=0, y = υy = β-gt, y= — g.
Подставляя найденные величины в (68), найдем касательное ускорение
Подставляя те же величины в формулу (72), найдем нормальное ускорение
Нормальное ускорение всегда направлено во внутрь траектории, отрицательный знак получился потому, что в этой задаче естественные оси взяты по левой системе, (ось М,— вправо, ось Mn — вниз), а неподвижные — по правой.
Ответ. 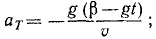
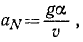
Задача №7
Найти скорость, полное, касательное и нормальное ускорения точки, описывающей фигуру Лиссажу, по уравнениям движения точки, заданным в координатной форме:
х= 3 sin 2t, у = 4 sin 2t.
Решение. Найдем сначала проекции скорости:
υχ = 6 cos 2t, υy = 8 cos 2t.
Затем определим величину полной скорости точки:
Для определения касательного и нормального ускорений определим проекции ускорения на декартовы оси координат, затем найдем полное ускорение и разложим его на касательное и нормальное. Имеем
ax= —12 sin 2t, ay =—16 sin 2t,
Найдем сначала касательное ускорение, для чего продифференцируем по времени полную скорость или воспользуемся формулой (68):
Мы видим, что полное ускорение по величине равно касательному ускорению, т. е. что нормальное ускорение равно нулю. Это возможно только в случае, если траектория — прямая линия. Для проверки можно определить кривизну траектории или найти уравнение траектории. По первому способу имеем
По второму способу найдем 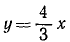
Ответ. υ=10 cos 2t; α = 20 sin 2t; ат= —20sin 2t; αN = 0.
Задача №8
Точка обода колеса, катящегося без скольжения и без буксования по прямолинейному рельсу, движется согласно уравнениям x=r (ct-sin сt), y=r(l — cos ct). Найти нормальное ускорение точки.
Решение. Для решения задачи можно наметить следующий путь: найти проекции скорости, величину полной скорости, проекции ускорения и полное ускорение; затем, продифференцировав по времени величину полной скорости, найти касательное ускорение и, вычитая его геометрически из полного, найти нормальное.
Дифференцируя уравнения движения, найдем
υx= rc (1 —cos ct), υy = rc sin ct.
Далее получаем
Дифференцируя проекции скорости, найдем
ax = rc2 sin ct, ay = rc2 cos ct
полое ускорение
а = rs2
Дифференцируя υ, найдем касательное ускорение:
Вектор aτ перпендикулярен вектору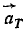
Задачи такого типа быстрее и короче решать с применением формулы (72). По этой формуле непосредственно получаем:
Ответ:
Задача №9
Тяжелое тело, размерами которого можно пренебречь, брошено с большой высоты с горизонтальной скоростью υ0 и движется согласно уравнениям x-υ0t, 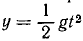
Решение. Определяя из первого уравнения t и подставляя во второе, найдем уравнение траектории:
Траектория—парабола (рис. 95). Дифференцируя уравнения движения по времени, найдем проекции скорости и по ним полную скорость:
В начальное мгновение (t = 0), скорость точки υ = υo, а затем с течением времени величина скорости непрерывно возрастает. Из полученного равенства определим время t, в течение которого тело приобретает скорость у:
Вторично дифференцируя уравнения движения точки, найдем проекции ускорения на оси координат и полное ускорение:
В данном случае тело движется с постоянным по модулю и направлению ускорением, параллельным оси Оу.
Обращаем внимание на то, что, хотя здесь a = const, движение точки не является равнопеременным, так как условием равнопеременного движения является не условие a = const, а условие aт= const. В данном же случае, как мы сейчас увидим, ат непостоянно.
Дифференцируя величину полной скорости по времени или непосредственно по (68), получим касательное ускорение
Подставляя вместо t найденное нами значение, выразим касательное ускорение aт через скорость υ:
Отсюда следует, что в начальное мгновение, когда υ = υ0, aт=0. Затем с увеличением υ величина ат растет и в пределе стремится к полному ускорению g.
Для нахождения нормального ускорения обратимся к (72). Имеем
В начальное мгновение (при t = 0 и υ=v0) aN=g, а затем с увеличением υ аN убывает, стремясь в пределе к нулю.
Ответ. Парабола
Задача №10
Определить радиус кривизны траектории точки в начале движения, если уравнения ее движения имеют вид: x = 2t, y = t2 (t— в cек; х, у— в м).
Решение. Из формулы кривизны (73) имеем
Для получения проекций скорости и ускорения в начальное мгновение продифференцируем уравнения движения и подставим t = 0:
Полную скорость в начальное мгновение определяем по ее проекциям:
Подставляя эти величины в формулу (73), получим ответ.
Ответ. р = 2 м
Задача №11
Через 20 сек после начала движения автомобиль, двигаясь иа закруглении радиуса 400 м, приобрел скорость 108 км/ч. Считая, что величина скорости автомобиля пропорциональна квадрату времени, определить полное ускорение автомобиля в конце 20-й секунды н пройденное за это время расстояние.
Решение. За единицы принимаем метр и секунду. Траектория задана—дорога с закруглением радиуса 400 м, и для решения задачи необходимо определить Уравнение движения автомобиля по траектории. (Применять формулы (71) здесь нельзя, так как при равиоперемениом движении величина скорости пропорциональна времени, а в данной задаче она пропорциональна квадрату времени.)
В условии дано
υ=bt2.
Найдем коэффициент пропорциональности
Выражая скорость по (53) и разделяя переменные, получим
откуда, интегрируя, получаем
Постоянную C определим из начальных данных: в начальное мгновение (t = 0) автомобиль не прошел еще никакого расстояния, а потому C = 0. Дважды дифференцируя по времени полученное уравнение, найдем касательное ускорение
или в конце 20-й секунды
αт=3 м/ceκ2.
Скорость в конце 20-й секунды была 30 м/сек, и по (74)
Полное ускорение в конце 20-й секунды было
Чтобы определить расстояние, пройденное автомобилем за 20 сек, положим в уравнении движения t = 20 сек:
Ответ. а = 3,75 м/сек2, s = 200 м.
- Основные законы динамики
- Колебания материальной точки
- Количество движения
- Момент количества движения
- Приведение системы сил к данной точке
- Система сил на плоскости
- Естественный и векторный способы определения движения точки
- Координатный способ определения движения точки
Как найти нормальное ускорение зная тангенциальное
Содержание
- Этот видеоурок доступен по абонементу
- На этом уроке мы вспомним, что такое ускорение. Рассмотрим две его составляющие, тангенциальную и нормальную, и пример нахождения этих составляющих. А также решим две задачи из сборника для подготовки к Единому государственному экзамену на нахождение радиуса траектории в наивысшей точке.
- Ускорение. Нормальная и тангенциальная составляющие ускорения
- Пример нахождения тангенциальной и нормальной составляющей ускорения
- Задача 1
- Задача 2
- Нахождение закона изменения скорости от времени
- В физике
- Траектория движения и компоненты полного ускорения
- Ускорение тангенциальное
- Ускорение нормальное
- Ускорение полное, нормальное и тангенциальное
- Решение задачи
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
Нормальное ускорение 
Здесь R – это радиус кривизны траектории в заданной точке.
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

Ускорение. Нормальная и тангенциальная составляющие ускорения
Механическое движение по характеру подразделяется на поступательное, вращательное и колебательное; по виду траектории – прямолинейное и криволинейное. Также механическое движение можно подразделять по характеру изменения скорости.
Физическая величина, которая определяет быстроту изменения скорости, называется ускорением. Математически ускорение определяется отношением изменения скорости к промежутку времени, за которое оно произошло (производная от скорости по времени):  и нормальную (перпендикулярную вектору скорости).</p>
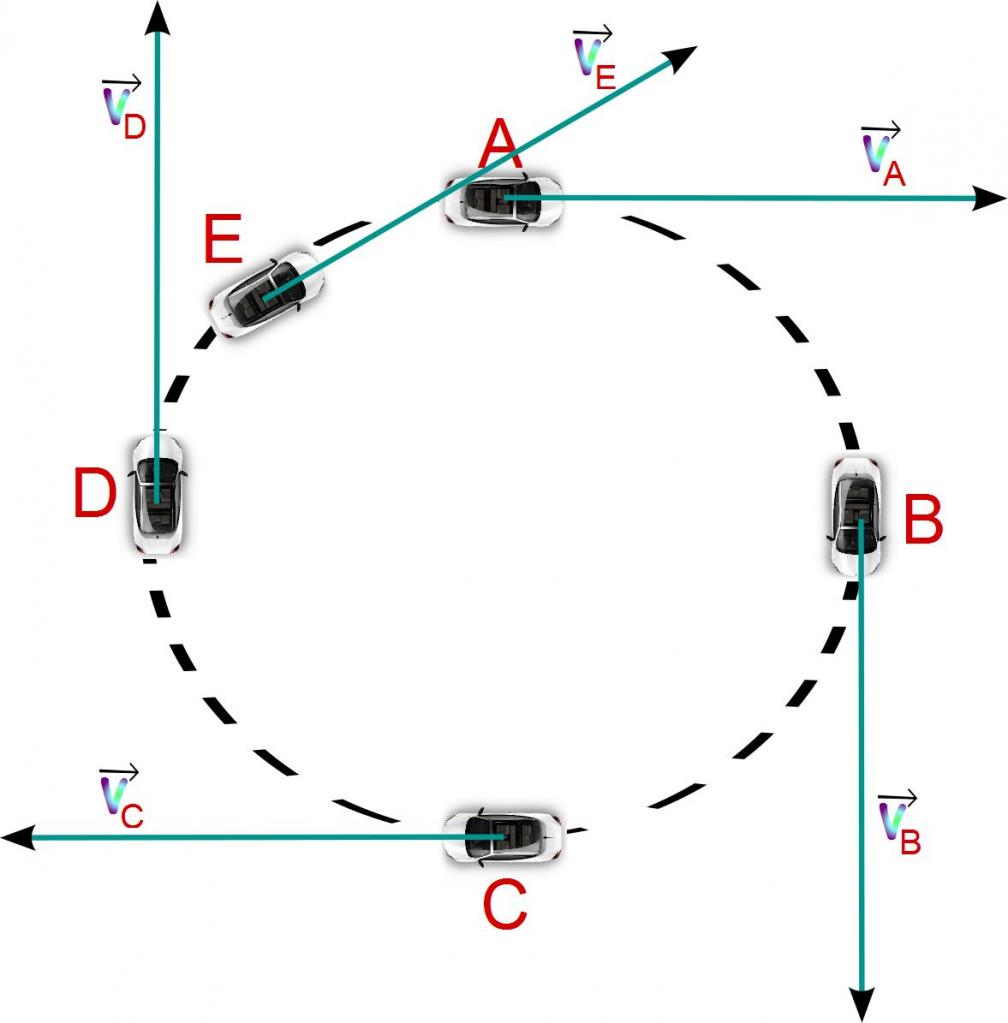
<p style=)
Рис. 1. Тангенциальная и нормальная составляющие полного ускорения
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.
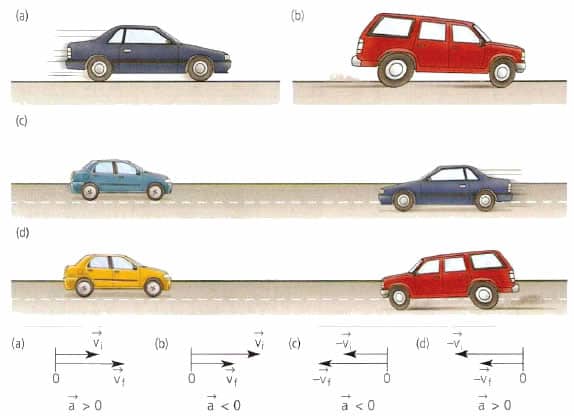
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное (см. рис. 2).
Рис. 2. Тангенциальная составляющая ускорения сонаправлена со скоростью
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным (см. рис. 3).
Рис. 3. Тангенциальная составляющая ускорения противонаправлена скорости
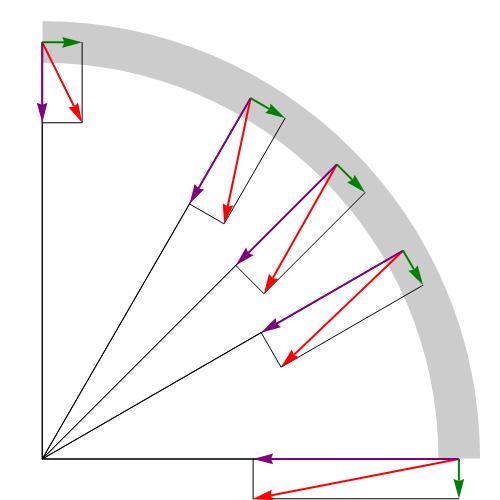
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).
Рис. 4. Направление нормального ускорения
Величина нормального ускорения связана с радиусом траектории и со скоростью движения следующим соотношением:
При прямолинейном движении тело имеет только тангенциальное ускорение. Нормальное ускорение отсутствует, так как скорость тела по направлению остаётся неизменной (см. рис. 5).
Рис. 5. Прямолинейное движение
При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения (см. рис. 6).
Рис. 6. Криволинейное движение
Пример нахождения тангенциальной и нормальной составляющей ускорения
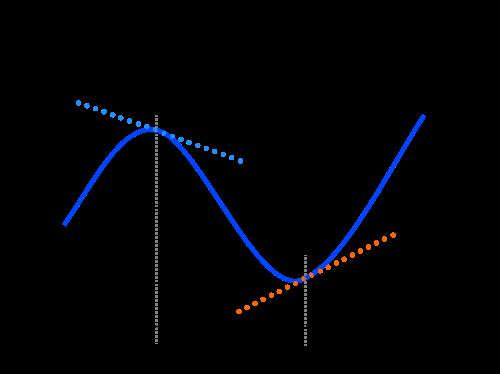
Рассмотрим движение тела, брошенного под углом к горизонту (см. рис. 7). Найдём составляющие ускорения в тот момент, когда скорость тела направлена под углом 
Рис. 7. Траектория движения тела
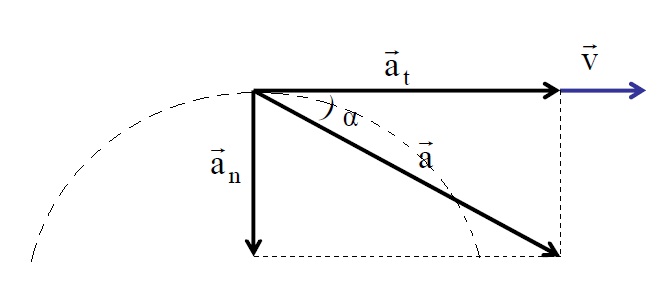
Касательная к траектории в точке A – это направление скорости
Рис. 8. Проекции ускорения
На рисунке видно, что тангенциальная составляющая ускорения направлена против скорости, то есть скорость тела в данный момент уменьшается (см. рис. 8). Нормальная составляющая ускорения направлена перпендикулярно скорости, следовательно, скорость в следующий момент наклонится в сторону 
Величины составляющих ускорения находим геометрически.
Рис. 9. Геометрическое определение величины составляющих ускорения
Угол A в треугольнике разложения на составляющие (треугольник выделен жёлтым на рисунке) имеет взаимно перпендикулярные стороны с углом 

Нормальная составляющая ускорения равна: 
Задача 1
Обод радиусом 1 метр катится по горизонтальной поверхности со скоростью 10 м/с. Найти радиус траектории точки поверхности обода при прохождении наивысшего положения.
Дано: 

Решение
Рис. 10. Иллюстрация к задаче
На рисунке изображён обод, который катится по горизонтальной поверхности со скоростью 


С центром обода у всех точек, лежащих на её поверхности, связано нормальное ускорение, так как оно направлено перпендикулярно скорости движения точки по окружности в любой момент времени.
Ускорение остаётся неизменным для всех точек поверхности обода, так как при переходе к системе отсчёта, связанной с Землёй, центр обода движется равномерно: 
Тогда для точки
В этой задаче заданное значение начальной скорости было лишним. Избыточные данные часто включают в задания ЕГЭ по физике.
Ответ: 
Задача 2
После удара футбольный мяч за 2 с пролетел 40 м и упал на землю. Чему равен радиус траектории мяча в верхней точке траектории?
Дано: 

Решение
Рис. 11. Иллюстрация к задаче
На рисунке изображена траектория полёта мяча (см. рис. 11). Точка A – верхняя точка траектории, скорость мяча в которой 

Следовательно, радиус траектории в верхней точке равен: 
Ответ: 
Нахождение закона изменения скорости от времени
Сведения об ускорении необходимы для того, чтобы найти закон изменения скорости от времени. Например, зависимость скорости от времени находится как неопределённый интеграл от ускорения по времени: 
При равноускоренном движении 

- Вопросы в конце параграфа 13 (стр. 46); — Касьянов В.А. Физика. 10 кл. (см. список рекомендованной литературы) (Источник)
- Камень брошен со скоростью 20 м/c под углом
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).
Траектория движения и компоненты полного ускорения
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь ut¯ — вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения — это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL — это пройденный телом путь за промежуток времени dt, r — радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
Теперь можно воспользоваться формулой для an:
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
Нормальное ускорение
Нормальное
ускорение – это составляющая
вектора ускорения, направленная вдоль
нормали к траектории движения в данной
точке на траектории движения тела. То
есть вектор нормального ускорения
перпендикулярен линейной скорости
движения (см. рис. 1.10). Нормальное ускорение
характеризует изменение скорости по
направлению и обозначается буквой
n.
Вектор нормального ускорения направлен
по радиусу кривизны траектории.
Полное ускорение
Полное
ускорение при криволинейном
движении складывается из тангенциального
и нормального ускорений по правилу
сложения векторов и
определяется формулой:
(согласно
теореме Пифагора для прямоугольно
прямоугольника).
Направление
полного ускорения также определяется
правилом
сложения векторов:
=
τ
+
n
4. Равномерное движение по окружности.
Среди
различных видов криволинейного движения
особый интерес представляет равномерное
движение тела по окружности. Это самый
простой вид криволинейного движения.
Вместе с тем любое сложное криволинейное
движение тела на достаточно малом
участке его траектории можно приближенно
рассматривать как равномерное движение
по окружности.
Центростремительное
ускорение.
При равномерном движении по окружности
значение скорости остается постоянным,
а направление вектора скорости
изменяется
в процессе движения. Определим ускорение
тела, движущегося равномерно по окружности
радиусом R.
За интервал времени Δt
тело проходит путь
.
Этот
путь Δs
равен длине дуги АВ
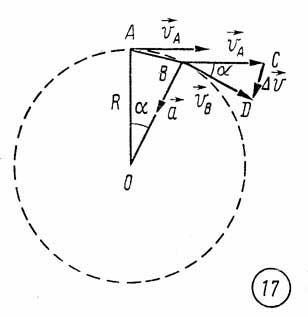
(рис. 17). Векторы
скоростей
и
точках
А
и В
направлены по касательным к окружности
в этих точках, угол α между векторами
и
равен
углу между радиусами ОА
и OB.
Для
нахождения вектора ускорения
нужно
найти разность векторов скорости
и
определить отношение изменения скорости
к малому интервалу времени Δt,
за который произошло это изменение:
.
Из
подобия треугольников ОАВ
и BCD
следует
.(3.1)
Если
интервал времени Δt
мал, то мал и угол α. При малых значениях
угла α длина хорды АВ
примерно равна длине дуги АВ,
т. е.
.
Так как
,
и
,
то из выражения (3.1) получаем
,(3.2)
.
(3.3)
Поскольку
,
(3.4)
из
выражений (3.3) и (3.4) получаем
.
(3.5)
Из
рисунка 17 видно, что, чем меньше угол α,
тем ближе направление вектора
к
направлению на центр окружности. Так
как вектор ускорения равен
отношению
вектора
к
интервалу времени Δt
при условии, что интервал времени Δt
очень мал, то вектор ускорения при
равномерном движении по окружности
направлен к ее центру.
При
изменении положения тела на окружности
меняется направление на центр окружности.
Следовательно, при равномерном движении
тела по окружности модуль ускорения
имеет постоянное значение, но направление
вектора ускорения изменяется со временем.
Ускорение при равномерном движении по
окружности называется центростремительным
ускорением.
5. Законы Ньютона.
Зако́ны Ньюто́на — три закона,
лежащие в основе классической
механики и позволяющие
записать уравнения
движения для любой механической
системы, если известны
силовые
взаимодействия для
составляющих её тел. Впервые в полной
мере сформулированы Исааком
Ньютоном в книге «Математические
начала натуральной философии»
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Иногда удобно рассмотреть скорость движения тела по окружности через угловую скорость. Она показывает, на какой угол успевает повернуться тело за единицу времени. На Рис.1. мотоциклист, переместившись из точки (A) в точку ({A}^{’}), повернулся на угол (Delta varphi) за время (t).
$$omega=frac{Deltavarphi}{t} , (рад/сек);$$
В международной системе единиц измерения угловую скорость принято измерять в радианах в секунду. Кроме обычных градусов углы можно измерять в радианах, с ними вы должны были столкнуться в школьном курсе тригонометрии.
И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.
Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок ({A}^{’}O) — точка (A) переходит в точку ({A}^{’}), а точка (B) – в точку ({B}^{’}).
При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности ({AA}^{’}), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние ({BB}^{’}).
Выпишем формулы для линейных скоростей точек (A) и (B):
$$V_{A}=frac{{AA}^{’}}{t};$$
$$V_{B}=frac{{BB}^{’}}{t};$$
Из рисунка 1 видно, что ({AA}^{‘}>{BB}^{‘}), а значит линейная скорость точки (A) больше скорости точки (B):
$$V_{A}>V_{B};$$
Можно сделать важный вывод, что чем дальше точка находится от центра, тем больше ее скорость относительно точек, находящихся на этой же прямой.
А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?
Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.
И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:
$$V=omega*R; ,,(1)$$
где (V) – линейная скорость,
(omega) – угловая скорость,
(R) – радиус вращения.
Тангенциальное ускорение
Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.
Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.
Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec{a_{/tau}}))
При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле:
$$a_{tau}=frac{V_к-V_н}{t};$$
где (V_к) – конечная скорость;
(V_н) – начальная скорость;
(t) – время, за которое скорость изменилась с (V_н) до (V_к).
При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.
Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).
Если тело движется по прямой, то нормальное ускорение равно (0).
Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec{a})).
Пример 2
Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса
Решение:
Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость:
$$a_n=omega^2*r;$$
Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3).
$$a_{nA}=omega^2*frac{R}{2};$$
$$a_{nB}=omega^2*frac{R}{3};$$
$$frac{a_{nA}}{a_{nB}}=frac{omega^2*frac{R}{2}}{omega^2*frac{R}{3}}=frac{R}{2}*frac{3}{R}=1,5$$
Ответ:(frac{a_{nA}}{a_{nB}}=1.5.)
Что такое центростремительное ускорение
Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.
Чему равно центростремительное ускорение
Модуль центростремительного ускорения определяется формулой:
[a_{n}=frac{v^{2}}{R}]
Модуль an остается постоянным, однако направление вектора an все время меняется, поэтому движение по окружности не является равноускоренным.
Центростремительное ускорение также можно определить через угловую скорость:
В общем случае ускорение движущейся по окружности точки можно представить в виде двух составляющих – нормальной и тангенциальной. Первая составляющая направлена по касательной к траектории, вторая по радиусу непосредственно к центру круга. Всё это можно представить в виде формулы:
[mathbf{a}=mathbf{d} v / d t=(d v / d t) * boldsymbol{tau}+v *(d tau / d t)=(mathrm{dv} / mathrm{dt}) * boldsymbol{tau}+left(mathrm{v}^{2} / mathrm{R}right) * mathbf{n}]
Где R – радиус окружности, n – единичный вектор нормали к траектории.
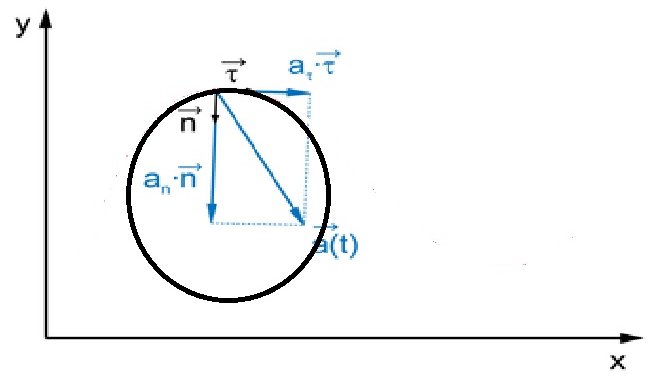
Тангенциальное ускорение
Это ускорение (dv/dt) * τ, оно характеризует изменение скорости по величине за единицу времени и является её производной. В системе СИ тангенциальное ускорение измеряется в м/c2. Оно может быть, как положительным, так и отрицательным. При положительных значениях тангенциального ускорения модуль скорости движущейся по окружности точки возрастает и движение именуют ускоренным. При отрицательных значениях величина скорости понижается и движение называют замедленным. Если тангенциальное ускорение постоянно, то к словам ускоренный и замедленный добавляется приставка «равно».
Нет времени решать самому?
Наши эксперты помогут!
Нормальное или центростремительное ускорение
Это вторая составляющая разложенного нами движения (v2/R)*n. Обозначим её как an Поясним, откуда взялись квадрат скорости, радиус и n.
Одновременно умножаем и делим v * (dτ/dt) на стремящийся к нулю элемент длины траектории, т. е. v*(dτ/dl)(dl/dt). Последний множитель в этом выражении есть скорость, его можно записать как v *(dτ/dl)*v. Отсюда v2*(dτ/dl). dl допустимо представить как R*dϕ. dϕ здесь есть малый угол поворота вокруг центра окружности.
n = dϕ/dτ. Это ясно из геометрических соображений. Δτ = τ ′- τ есть разность единичных касательных векторов в рассматриваемой нами точке (τ) и бесконечно близкой к ней точке (τ ′). По величине она равна 2sin(dϕ/2). Здесь dϕ есть угол между τ и τ ′. Эта разность в рассматриваемой точке имеет направление к нормали n под углом dϕ/2. Из-за малости dϕ становится возможным совпадение его с вектором нормали n. Также из-за малости dϕ синус допустимо разложить в ряд Тейлора. В результате всего этого мы приходим к тому, что Δτ = Δϕ * n. Для бесконечно малых это выражение переходит в dτ = dϕ * n.
Мгновенную скорость можно выразить соотношением v =ω*R. После этого формула центростремительного ускорения приобретает у нас вид an = (ω*R)2/R = ω2*R.
Теперь о том, в чем измеряется центростремительное ускорение в физике. Хотя некоторым может показаться странным, но меряется оно, также как и тангенциальное ускорение в метрах на секунду квадрат, т. е. м/c2.
Первым (или одним из первых), кто стал пользоваться понятием центростремительного ускорения, был по-видимому Христиан Гюйгенс. Именно с его времени понятие нормального ускорения в физике начали повсеместно применять при решении самых разных механических задач.
Примеры решения задач
Примеры
Задача №1.
Поезд движется со скоростью 54 километра в час по закруглению, радиус которого равен 1 километру.
Найти чему равно его центростремительное ускорение.
Дано:
Радиус R = 1 км = 1000 м.
Скорость v = 54 км/ч = 15 м/с.
Найти нужно нормальное ускорение [a_{n}].
Решение:
Формула центростремительного ускорения в физике нам известна [a_{n}=v^{2} / R]. Подставляем в неё наши
числовые значения и находим [a_{n}=(15 м/с)^{2} / 1000=0,225 м/
с^{2}].
Ответ: [a_{n}=0,225 м/с^{2}].
Задача №2.
Тело движется по траектории радиусом 5 метров с угловой скоростью 0,3 радиан в секунду. Требуется найти его
центростремительное ускорение.
Дано:
Радиус R = 5 м.
Угловая скорость [omega=0,3 text { рад/с }]
Найти центростремительное ускорение [a_{n}].
Решение:
Опять подставляем числовые значения, но уже в формулу [a_{n}=omega^{2} * R].
[a_{n}=5^{2 *} 0,3=0,45 м/с^{2}].
Ответ: [a_{n}] равно [0,45 м/с^{2}]
Задача №3.
Диск вращается вокруг неподвижной оси. Угол поворота диска изменяется в соответствие с уравнением ϕ = 5t+7.
Нужно вычислить, чему равно центростремительное ускорение очки диска, расположенной на расстоянии R от оси
вращения равном 0,5 м на 4 секунду от времени начала вращения.
Дано:
Радиус R = 0,5 м.
Время t = 4 c.
Закон движения ϕ = 5t+7 .
Найти [a_{n}].
Решение:
Формула центростремительного ускорения, включающая угловую скорость [a_{n}=omega^{2 *} R].
Угловую скорость можно найти по формуле [omega=d phi / d t].
Подставляем вместо ϕ уравнение изменения угла поворота [omega=d(5 t+7) / d t].
Производная этого выражения равна 10t.
Теперь нужно подставить вместо t конкретное числовое значение, т.е. 4 секунды.
Получаем [a_{n}=10 * 4=40 м/с^{2}].
Ответ: [a_{n}] точки на диске равно [40 м/с^{2}].

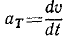
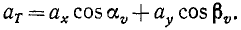
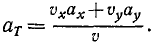
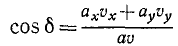
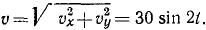
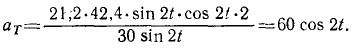
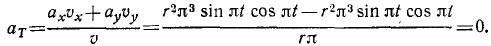
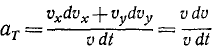
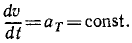
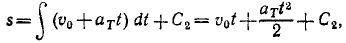
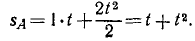
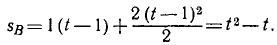
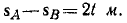
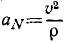
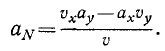
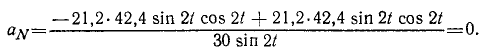
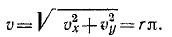
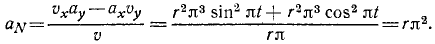
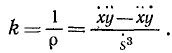
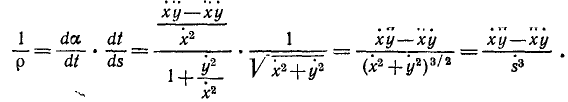
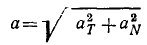
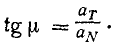
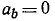
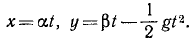
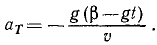
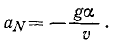
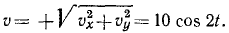
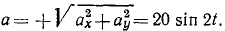
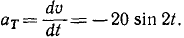
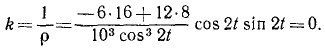
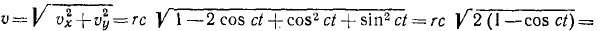
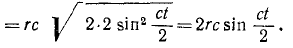
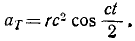
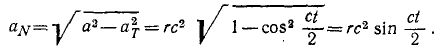
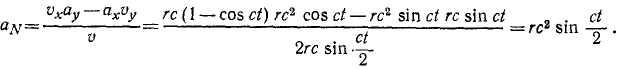
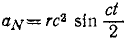
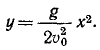
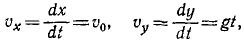
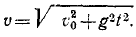
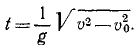
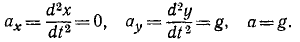
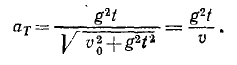
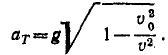
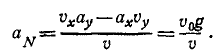
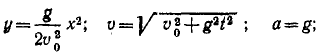
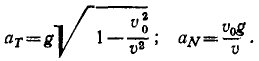
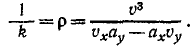
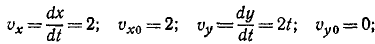
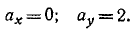
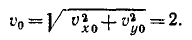
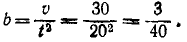
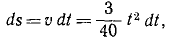
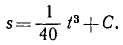
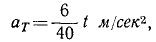
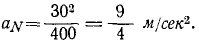
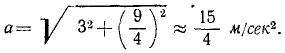
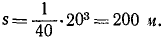


.</p>
<p style=)




















.</li>
<li>Интернет-портал Gym1belovo.smartlearn.ru (Источник).</li>
<li>Интернет-портал Studopedia.info (Источник).</li>
</ol>
<p style=) Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.