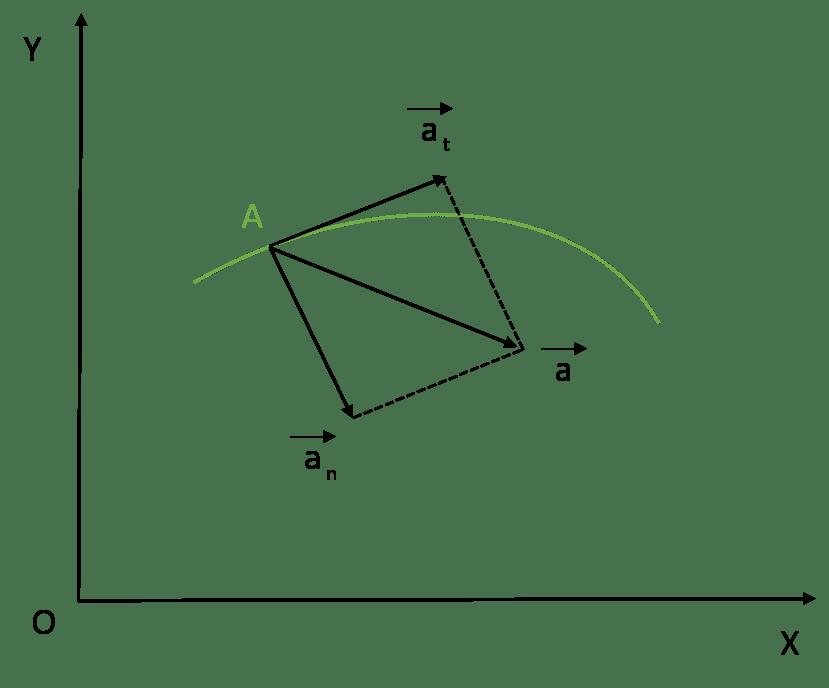
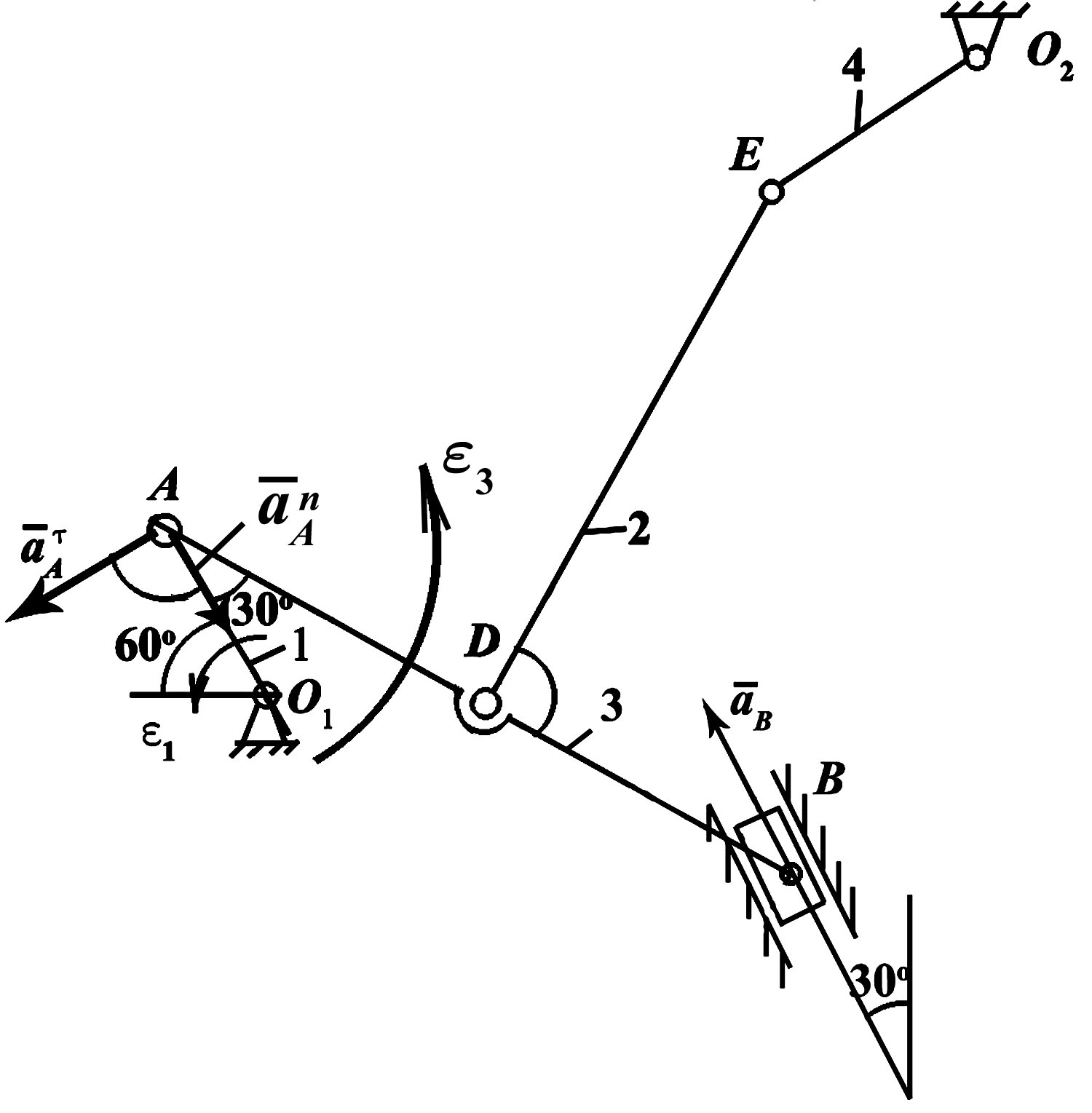
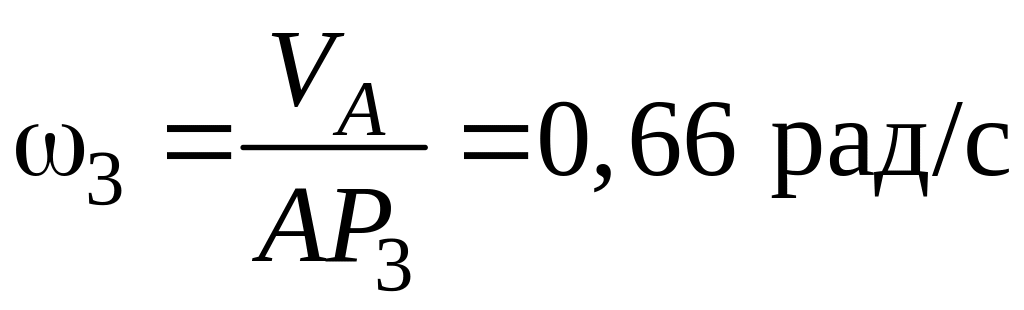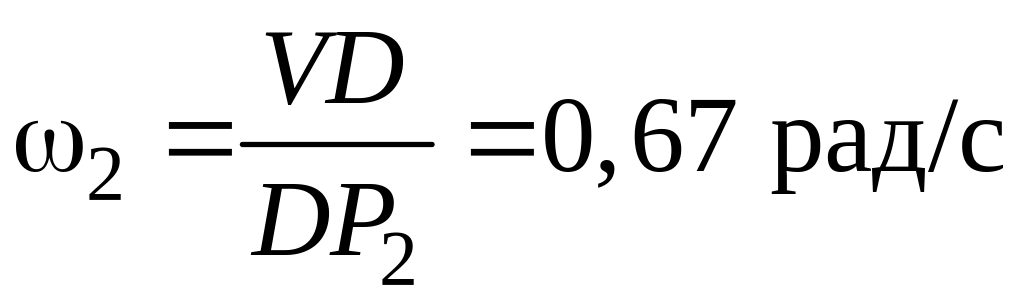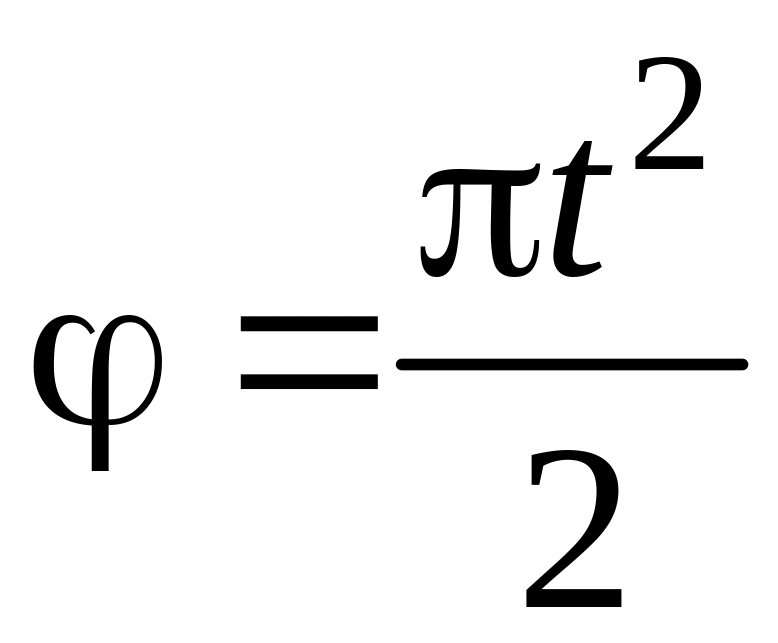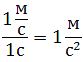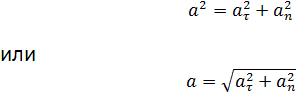Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Задача
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t3 (s в метрах, t в секундах).
Рисунок 1.6
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
Другие примеры решений >
Помощь с решением задач >
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
Другие видео
Скорость точки направлена по касательной к траектории (окружности), т.е. перпендикулярно линии радиуса.
Подставляя в предыдущее выражение значение скорости, получим 6=13,5t12, откуда находим
Касательное ускорение для любого момента времени равно
При t=t1=2/3 с
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
Модуль вектора полного ускорения точки равен
Направление нормального, касательного и полного ускорений точки
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
отсюда
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Тангенциальное ускорение — определение, формула и измерение
Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
- Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
- Нормальное — совпадающее с нормалью траектории изменения положения.
- Полное — определяющееся суммой тангенциального и нормального ускорений.
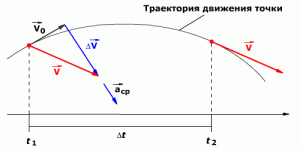
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
- Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
- Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
- at — тангенциальной составляющей, совпадающей с отрезком V;
- an — перпендикулярным по отношению расположения V вектором.
Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2 .
Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
- Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t 3 . Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения. Подставив заданные значения, можно получить: w = d φ / dt = -1 + 0,2 * 3t 2 и e = dw / dt = 0,6 * 2t. Применив формулу связи, легко найти ускорение: at = R * E * (0,6 * 2t) = 1,2 * Rt = 24 м 2 /с. Подставив в формулу нормального ускорения значения, можно вычислить и его an = V 2 / R = R * (0,6 * 10 2 — 1) 2 / 0,2 = 696 м/с 2 . Отсюда полное ускорение будет равняться: a = √ 24 2 + 696 2 = 697 м/с 2 .
- Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at. При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Сложная задача
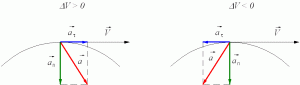
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Нормальное ускорение можно выразить через скорость и радиус: an = V 2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V 2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V 2 / R = — dV / dt.
Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V 2 . В итоге должно получиться выражение: dV / V 2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
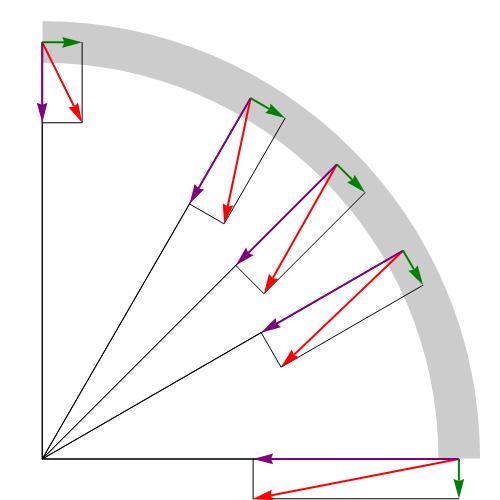
Движение материальной точки по окружности. Центростремительное ускорение.
Линейная и угловая скорости
Движение по окружности нас окружает постоянно – это может быть мотоциклист на мототреке, вращение грузика на веревке, движение по выгнутому круглому мосту, любой поворот на дороге тоже можно рассматривать, как движение по части окружности и т.д.
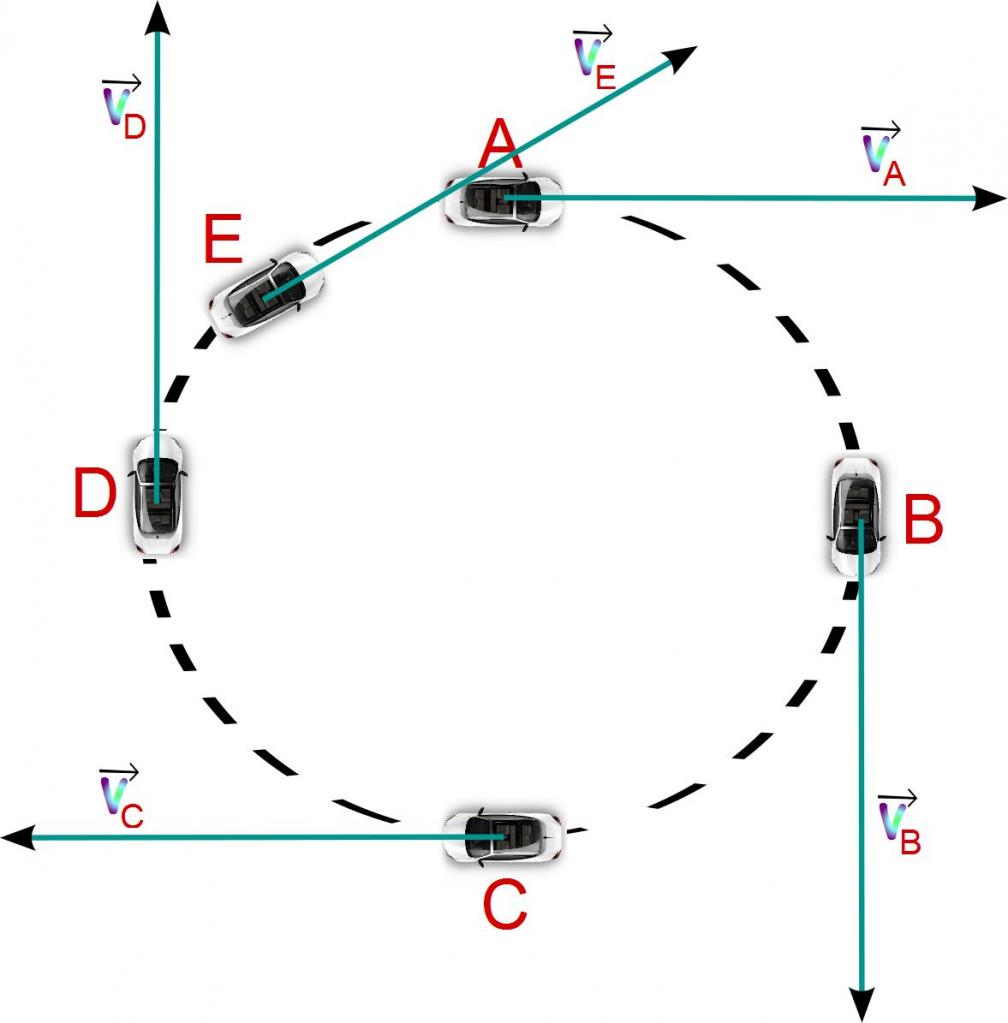
Давайте представим, что мы смотрим сверху на мототрек (см. рис.1.). Пусть точка (А) это мотоциклист, который движется с постоянной линейной скоростью (vec), и за какое-то время (t) он переместится по дуге окружности (^<’>) в точку (^<’>). Его пройденный путь будет равен длине дуги окружности (^<’>).
Определение Линейная скорость – это путь, который проходит мотоциклист за единицу времени (например, за секунду):
Понятно, что чем больший путь (большую длину дуги) успевает пройти тело за одно и тоже время, тем быстрее оно движется, тем больше его линейная скорость. Линейная скорость — это обычная скорость, к которой мы все привыкли. Обратите внимание, что вектор линейной скорости всегда направлен по касательной к траектории, в нашем случае – по касательной к окружности. Чуть позже нам это пригодится.
И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.
Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок (^<’>O) — точка (A) переходит в точку (^<’>), а точка (B) – в точку (^<’>).
При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности (^<’>), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние (^<’>).
А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?
Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.
И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:
где (V) – линейная скорость,
(omega) – угловая скорость,
(R) – радиус вращения.
Период и частота вращения
Важными характеристиками любого вращательного движения являются частота и период:
Определение Период – время, за которое тело совершает полный оборот.
В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.
Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac<2*pi*R>;$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac<2*pi><omega>;$$ Где (V) –линейная скорость вращения.
В системе СИ период измеряется в ([^<-1>]).
Определение Частота – количество оборотов за единицу времени.
В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.
Период и частота вращения связаны между собой выражением: $$T=frac<1><nu>;$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac<2*pi*R>=frac<omega><2*pi>;$$
Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.
Решение: Точка (А) находится дальше от центра на (20 (см)), а значит ее скорость больше, чем у точки (В). По условию так и есть. Так как обе точки находятся на одном радиусе, то угловые скорости у них одинаковые. Распишем угловые скорости для точек (А) и (В) и приравняем: $$omega_A=frac;$$ $$omega_B=frac;$$ $$omega_A=omega_B;$$ $$frac=frac;$$ Из условия (A0=BO+0.2): $$frac=frac;$$ $$frac<15>=frac<10>;$$ $$15*BO=(BO+0,2)*10;$$ $$5*BO=2;$$ $$BO=0,4.$$ Мы нашли радиус окружности по которой вращается точка (В), тогда радиус точки (А) будет на (0,2(м)) больше — (0,6(м)).
Для того, чтобы найти частоту, воспользуемся формулой: $$nu=frac<2*pi*R_A>=frac<15><2*3,14*0,6>=3,98(об/сек);$$ Ответ: (R=0,6(м)) и (nu=3,98(об/сек).)
Центростремительное (нормальное) ускорение
Вернемся к нашему примеру с мотоциклистом, двигающимся по мототреку в форму окружности. (См. Рис.3.) Для начала, представим, что линейная скорость у мотоциклиста постоянна, то есть он двигается равномерно, а значит его ускорение должно быть равно нулю. Это действительно так, но при движении по окружности (или любой другой криволинейной траектории) даже с постоянной скоростью возникает новый вид ускорения – центростремительное, еще его называют «нормальное», ускорение. Оно появляется по причине изменения направления вектором скорости.
На самом деле, для решения задач понимать природу центростремительного ускорения совсем необязательно. Достаточно просто помнить, что при любом криволинейном движении появляется такое ускорение. Его можно вычислить по формуле: $$a_n=frac;$$ где (V) –линейная скорость;
(R) – радиус окружности.
Подставим сюда линейную скорость через угловую — (V=omega*R). И получим еще одну формулу для центростремительного ускорения: $$a_n=omega^2*R;$$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.
Тангенциальное ускорение
Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.
Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.
Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec>))
При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле: $$a_<tau>=frac;$$ где (V_к) – конечная скорость;
(V_н) – начальная скорость;
(t) – время, за которое скорость изменилась с (V_н) до (V_к).
При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.
Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).
Если тело движется по прямой, то нормальное ускорение равно (0).
Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec)).
Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса
Решение: Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость: $$a_n=omega^2*r;$$ Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3). $$a_=omega^2*frac<2>;$$ $$a_=omega^2*frac<3>;$$ $$frac>>=frac<omega^2*frac<2>><omega^2*frac<3>>=frac<2>*frac<3>=1,5$$ Ответ:(frac>>=1.5.)
http://nauka.club/fizika/tangentsialno%D0%B5-uskoreni%D0%B5.html
http://sigma-center.ru/circularmotion
Как найти нормальное ускорение зная тангенциальное
Содержание
- Этот видеоурок доступен по абонементу
- На этом уроке мы вспомним, что такое ускорение. Рассмотрим две его составляющие, тангенциальную и нормальную, и пример нахождения этих составляющих. А также решим две задачи из сборника для подготовки к Единому государственному экзамену на нахождение радиуса траектории в наивысшей точке.
- Ускорение. Нормальная и тангенциальная составляющие ускорения
- Пример нахождения тангенциальной и нормальной составляющей ускорения
- Задача 1
- Задача 2
- Нахождение закона изменения скорости от времени
- В физике
- Траектория движения и компоненты полного ускорения
- Ускорение тангенциальное
- Ускорение нормальное
- Ускорение полное, нормальное и тангенциальное
- Решение задачи
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
Нормальное ускорение 
Здесь R – это радиус кривизны траектории в заданной точке.
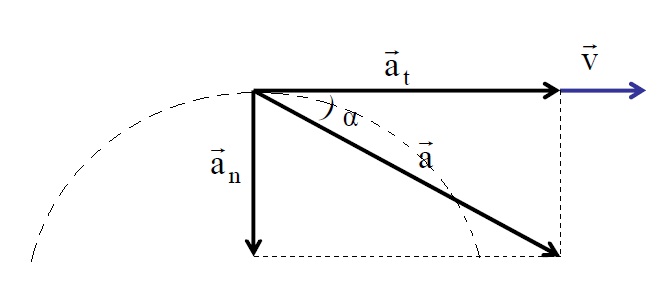
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

Ускорение. Нормальная и тангенциальная составляющие ускорения
Механическое движение по характеру подразделяется на поступательное, вращательное и колебательное; по виду траектории – прямолинейное и криволинейное. Также механическое движение можно подразделять по характеру изменения скорости.
Физическая величина, которая определяет быстроту изменения скорости, называется ускорением. Математически ускорение определяется отношением изменения скорости к промежутку времени, за которое оно произошло (производная от скорости по времени):  и нормальную (перпендикулярную вектору скорости).</p>
<p style=)
Рис. 1. Тангенциальная и нормальная составляющие полного ускорения
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное (см. рис. 2).
Рис. 2. Тангенциальная составляющая ускорения сонаправлена со скоростью
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным (см. рис. 3).
Рис. 3. Тангенциальная составляющая ускорения противонаправлена скорости
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).
Рис. 4. Направление нормального ускорения
Величина нормального ускорения связана с радиусом траектории и со скоростью движения следующим соотношением:
При прямолинейном движении тело имеет только тангенциальное ускорение. Нормальное ускорение отсутствует, так как скорость тела по направлению остаётся неизменной (см. рис. 5).
Рис. 5. Прямолинейное движение
При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения (см. рис. 6).
Рис. 6. Криволинейное движение
Пример нахождения тангенциальной и нормальной составляющей ускорения
Рассмотрим движение тела, брошенного под углом к горизонту (см. рис. 7). Найдём составляющие ускорения в тот момент, когда скорость тела направлена под углом 
Рис. 7. Траектория движения тела
Касательная к траектории в точке A – это направление скорости
Рис. 8. Проекции ускорения
На рисунке видно, что тангенциальная составляющая ускорения направлена против скорости, то есть скорость тела в данный момент уменьшается (см. рис. 8). Нормальная составляющая ускорения направлена перпендикулярно скорости, следовательно, скорость в следующий момент наклонится в сторону 
Величины составляющих ускорения находим геометрически.
Рис. 9. Геометрическое определение величины составляющих ускорения
Угол A в треугольнике разложения на составляющие (треугольник выделен жёлтым на рисунке) имеет взаимно перпендикулярные стороны с углом 

Нормальная составляющая ускорения равна: 
Задача 1
Обод радиусом 1 метр катится по горизонтальной поверхности со скоростью 10 м/с. Найти радиус траектории точки поверхности обода при прохождении наивысшего положения.
Дано: 

Решение
Рис. 10. Иллюстрация к задаче
На рисунке изображён обод, который катится по горизонтальной поверхности со скоростью 


С центром обода у всех точек, лежащих на её поверхности, связано нормальное ускорение, так как оно направлено перпендикулярно скорости движения точки по окружности в любой момент времени.
Ускорение остаётся неизменным для всех точек поверхности обода, так как при переходе к системе отсчёта, связанной с Землёй, центр обода движется равномерно: 
Тогда для точки
В этой задаче заданное значение начальной скорости было лишним. Избыточные данные часто включают в задания ЕГЭ по физике.
Ответ: 
Задача 2
После удара футбольный мяч за 2 с пролетел 40 м и упал на землю. Чему равен радиус траектории мяча в верхней точке траектории?
Дано: 

Решение
Рис. 11. Иллюстрация к задаче
На рисунке изображена траектория полёта мяча (см. рис. 11). Точка A – верхняя точка траектории, скорость мяча в которой 

Следовательно, радиус траектории в верхней точке равен: 
Ответ: 
Нахождение закона изменения скорости от времени
Сведения об ускорении необходимы для того, чтобы найти закон изменения скорости от времени. Например, зависимость скорости от времени находится как неопределённый интеграл от ускорения по времени: 
При равноускоренном движении 

- Вопросы в конце параграфа 13 (стр. 46); — Касьянов В.А. Физика. 10 кл. (см. список рекомендованной литературы) (Источник)
- Камень брошен со скоростью 20 м/c под углом
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).
Траектория движения и компоненты полного ускорения
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь ut¯ — вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения — это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL — это пройденный телом путь за промежуток времени dt, r — радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
Теперь можно воспользоваться формулой для an:
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
В
различные моменты времени точка движется
по прямо- и криволинейным участкам
траектории. На прямолинейных участках
полное ускорение точки равно ее
касательному ускорению, а на криволинейных
точка имеет еще и нормальное ускорение.
Его величина определяется по формуле:
,
где V
– скорость точки в интересующий момент
времени (находится по рис. 6, б или 6, г);
– радиус кривизны
траектории в том месте, где находится
в этот момент движущаяся точка (см. п. 1
и таблицу изменение дуговых координат
и пройденные пути).
Например, при t1
= 1 с: точка проходит положение М1
на криволинейном участке траектории
радиусом
= R2
= 20/
= 6,37 м со скоростью V1
= 5 м/с. Поэтому
м/с2.
Это ускорение
направлено к центру кривизны данного
участка траектории, т. е. к точке О2
(рис. 6, в).
Полное ускорение
точки в этот момент равно:
м/с2.
Непосредственно
перед моментом времени t2
= 2 с точка еще находится на том же
криволинейном участке траектории и
поэтому в этот момент она имеет касательное
ускорение (рис. 6, в), равное 10 м/с2
и нормальное ускорение аn
= 202/6,37
= 62,8 м/с2.
А полное ускорение
м/с2.
Сразу после момента
времени t2
= 2 c
исчезает и касательное, и нормальное
ускорение точки.
Подобный анализ
можно провести и для других моментов
времени.
Методические
указания к решению задач К-3 и К-4
Данные задачи –
на исследование и преобразование
простейших движений твердого тела
(поступательных и вращательных вокруг
неподвижных осей). Для их решения
необходимо знание следующих вопросов:
-
угловая
скорость тела и его изображение на
рисунках в виде вектора; -
линейные скорости
точек тела, движущегося поступательно,
и тела, вращающегося вокруг неподвижной
оси; их свойства, картины распределения; -
механические
передачи: назначение; классификация –
простые, сложные; виды – ременные,
зубчатые, цепные и т. п.; физические и
кинематические условия нормальной
работы любой механической передачи; -
понятие о
передаточном отношении и его вычислении
в случае простых и сложных передач.
Приступая к решению
задач необходимо проанализировать
какие простые передачи входят в состав
заданной сложной, установить как они
связаны между собой – последовательно
или параллельно (т. е. как происходит
передача движений: то ли от одного вала
к другому, от него к третьему и т. д., или
от одного вала – сразу и ко второму, и
к третьему); выделить точки, через которые
осуществляется передача движений от
одного тела к другому. Лишь после такого
последовательного анализа можно
приступать к формальным вычислениям,
чтобы последовательно ответить на
поставленные вопросы.
В задаче К-3
предварительно, независимо от исходных
данных таблицы, необходимо по схеме
установить картину движения механизма
в положительном направлении, т. е. в
каком направлении должны вращаться
колеса, шкивы, звездочки вокруг своих
неподвижных осей, в каком направлении
(влево, вправо, вверх, вниз) при этом
должна двигаться зубчатая рейка или
груз, и показать эти направления на
рисунке кинематической схемы. Исходным
условием является заданное на рисунке
кинематической схемы направление
движения точки М
в положительную сторону.
Если при последующих
вычислениях окажется, что угловая
скорость указанного тела или линейная
скорость заданной точки окажутся
отрицательными, то это будет означать,
что движение всего механизма происходит
в обратном направлении. Чтобы в дальнейших
вычислениях не иметь дело с отрицательными
числами, следует тотчас приступать к
выполнению рисунка с истинной картиной
его движения, а во всех последующих
вычислениях игнорировать отрицательные
знаки угловых и линейных скоростей и
ускорений.
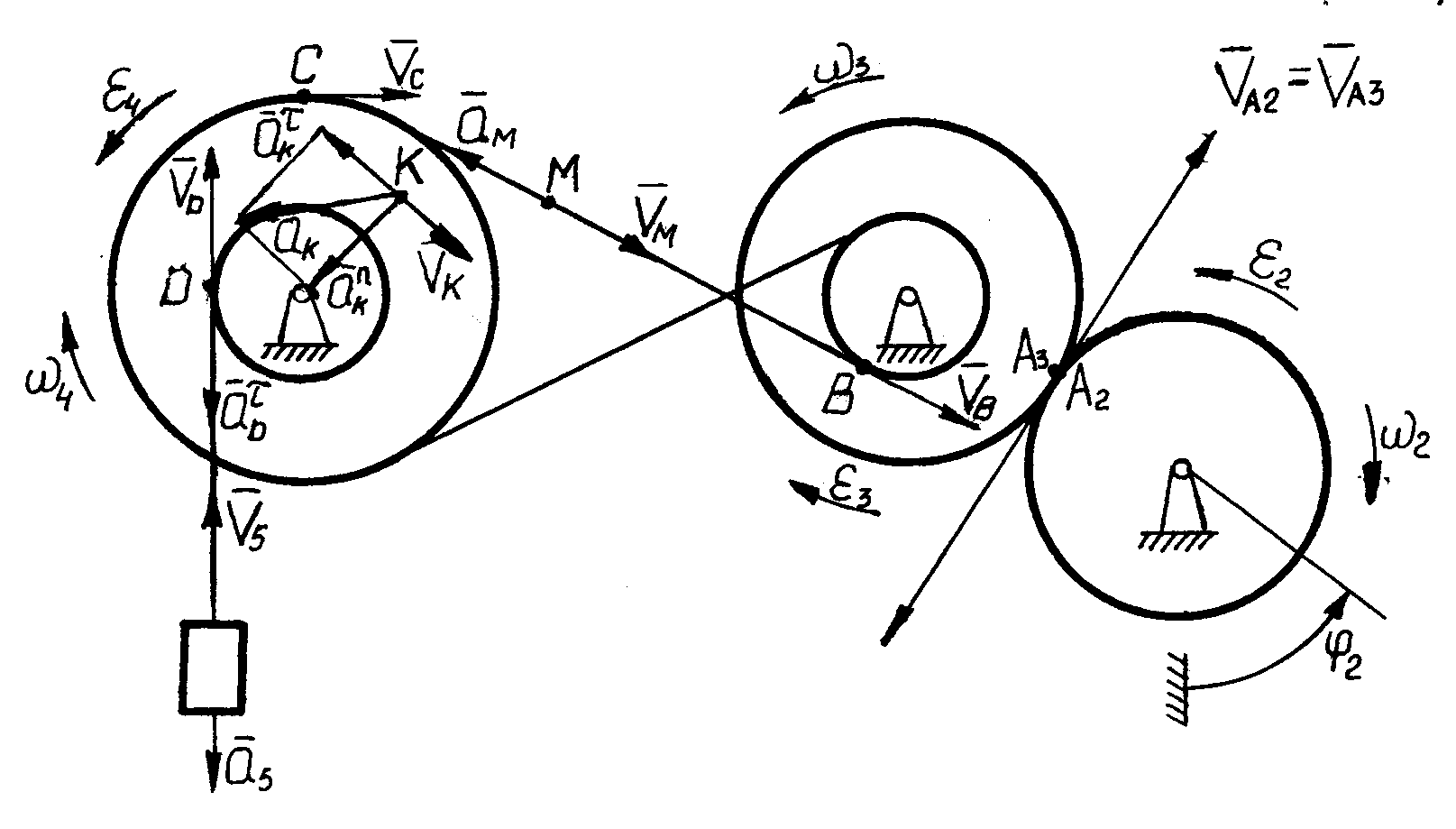
Пример
5
Вычислить
модули и указать направление кинематических
параметров, характеризующих движение
тел и точек системы в момент времени t1
= 2 c,
если дано
уравнение вращения тела 2.
2=40
e—t
– t2
(рад).
При вычислениях
принять:
-
количество зубьев
колес зубчатой передачи z2
= 20, z3
= 40; -
диаметры шкивов
ременной передачи d3
= 20 см, D4
= 60 см; -
диаметр барабана
d4
= 20 см; -
удаление точки К
от оси вращения тела 4 hk
= 20 см.

Рис. П.7
Решение
Выполняем
черновой рисунок (здесь он не приводится),
показывающий картину движения механизма.
Картину движения механизма в положительном
направлений т. е. колесо 2 вращается
против хода часовой стрелки (в сторону
увеличения угла 2,
показанного на одном рисунке). И
последовательно переходит от тела 2 к
телу 3, а от него к телу 4 получаем, что
колесо 4 вращается тоже против хода
часовой стрелки и груз 5 опускается
вниз. Это – картина движения механизма
в положительном направлении.
По заданному
уравнению вращения тела 2 находим его
дуговую координату 2(t1),
угловую скорость 2(t1)
и угловое ускорение 2(t1)
в момент времени t1:
рад/с;
рад/с2.
При t1
= 2 c:
2(t1)
= 1,41 рад; 2(t1)
= – 9,41 рад/с; 2(t1)
= 3,41 рад/с2.
Выполняем новый
рисунок (рис. 
передачи, показав на нем истинные
направления 2
= 9,41 рад/с (по часовой стрелки), 2
= 3,41 рад/с2
(против часовой стрелки) и координату
2
= 1,41 рад
а2
= а3
Рис. П.8
Для нормальной
работы механических передач необходимо,
чтобы не происходило проскальзывание
тел, входящих в контакт друг с другом,
а продольные деформации ремня (цепи)
были пренебрежимо малы. Эти требования
приводят к кинематическим условиям:
линейные скорости точек тел, через
которые осуществляется их контакт,
должны быть равны по величине и одинаковы
по направлению, и, кроме этого, все точки
ремня (цепи) должны иметь одинаковые по
величине линейные скорости.
С учетом этих
условий определяем угловые скорости
тел системы в момент времени t1
= 2 с, выражая линейные скорости точек
контакта через геометрические параметры
и угловые скорости соответствующих
тел.
VА3
= VА2,
т. е. 3R3
= 2R2
.
Следовательно,
.
Здесь
отношение радиусов заменено отношением
чисел зубьев, количество которых на
каждом колесе пропорционально его
радиусу (диаметру).
Из равенства
линейных скоростей точек А2
и А3
(А2
2, А3
3) следует равенство касательных ускорений
этих точек, поскольку а
= dV/dt.
А т. к.
= d/dt,
то
рад/с2.
Аналогично находим
VВ
= VМ
= VС,
т. е. 3r3
= 4R4.
Откуда
рад/с;
рад/с2.
Истинные направления
4
и 4,
вектора VВ,
VМ,
VС
показываем на рисунке (рис. П.8).
Далее, V5
= VD,
а5=
аD.
Следовательно,
см/с;
см/с2.
Определяем скорость
и ускорение точки К
в момент времени t1
= 2 с:
см/с;
,
где
см/с2,
направлено к оси вращения тела 4.
см/с2;
см/с2.
Показываем на
рисунке направления скорости и ускорений
точки К.
Так как вращение
колеса 2 в данный момент времени происходит
замедленно (2(t1)
и 2(t1)
имеют разные знаки и направления), то
весь механизм движется замедленно.
Линейные скорости и касательные ускорения
всех точек механизма направлены
противоположно друг другу.
Пример
6
Дано:
z1
= 25; z2
= 40; z2
= 20; z3
= 50; z3
= 40; z4
= 180. Скорость
набегания троса на
барабан
.
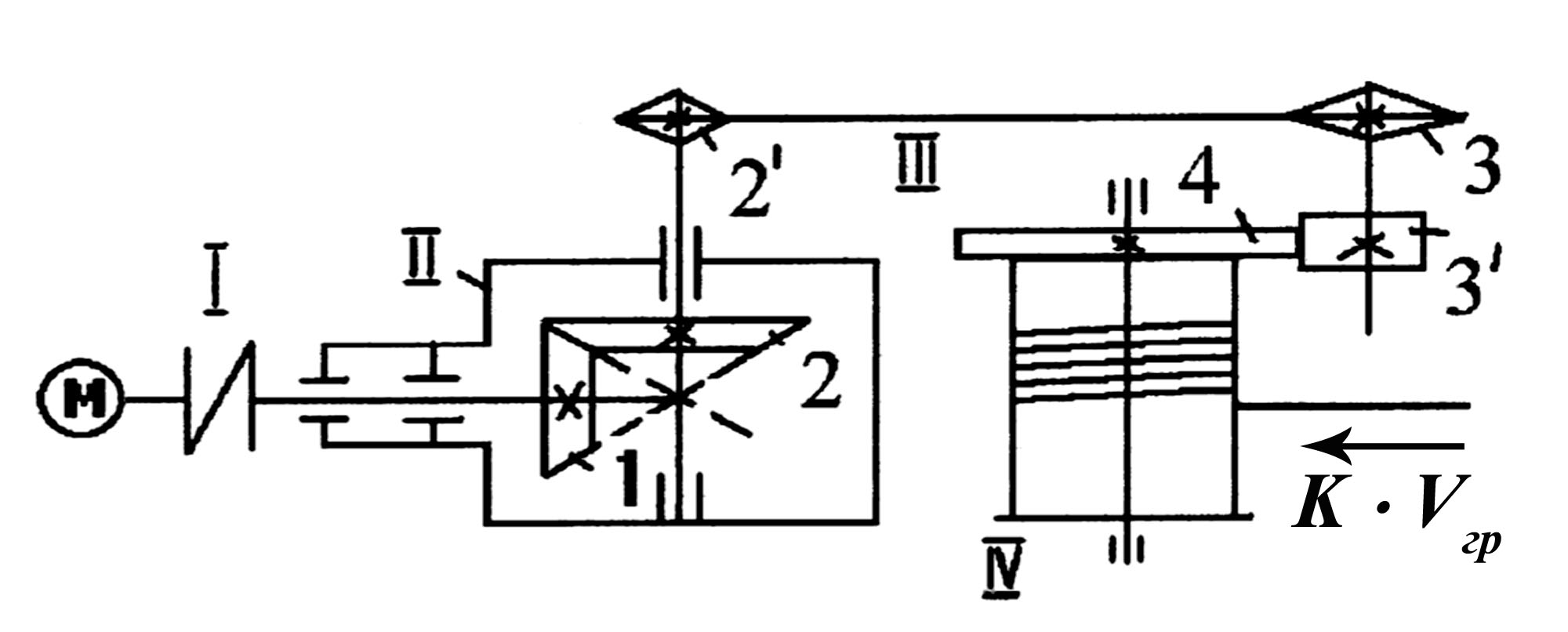
Рис. П.9
Решение
1. Определяем
передаточное отношение привода. Так
как его элементы соединены последовательно,
то
,
где дв
4
– угловые скорости двигателя и барабана;
,
– передаточное
отношение конической зубчатой передачи;
,
– передаточное
отношение цепной передачи;
,
– передаточное
отношение открытой зубчатой передачи
3
– 4.
Следовательно,
Uпр
= 1,62,54,5
= 18,0.
2. Произведем подбор
диаметра барабана Dб
и частоты вращения вала двигателя nдв.
Трос набегает на
барабан со скоростью V.
Учитывая, что при отсутствии проскальзывания
троса относительно барабана эта скорость
равна
а также что б
= дв/Uпр,
получаем, что требуемая скорость будет
обеспечена, если
nдвDб
=
В рассматриваемом
примере:
nдвDб
=
(моб/мин).
(nдв
– в об/мин, Dб
– в м).
Дальнейшие расчеты
удобно свести в таблицу.
|
№ п/п |
n, |
Диаметр |
Расхождение |
|
|
Требуемый |
Принимаемый |
|||
|
1 |
2850 |
150,78 |
150 |
0,517 |
|
2 |
1425 |
301,56 |
300 |
0,517 |
|
3 |
950 |
452,33 |
500 |
10,6 |
|
4 |
720 |
596,59 |
600 |
0,517 |
|
5 |
580 |
740,89 |
800 |
7,98 |
Из таблицы видно,
что варианты 1, 2 и 4 обеспечивают наибольшую
точность. Но от варианта с nдв
= 2850 об/мин и Dб
= 150 мм следует отказаться: при маленьком
диаметре потребуется слишком большая
длина барабана, чтобы обеспечить
необходимый объем для приема троса. А
многослойная навивка троса неизбежно
приведет к увеличению скорости набегания
троса на барабан и, в конечном счете, –
к перегрузке привода. Слишком большой
диаметр барабана и низкоскоростной
привод (вариант 4) приведут к неоправданному
увеличению нагрузок.
Принимаем nдв
= 1425 об/мин и Dб
= 300 мм
3. Определяем
угловые скорости валов привода:
(муфта
не изменяет скорость вращения соединяемых
валов).


Это – угловая
скорость барабана. Скорость навивки
троса:
4. Направление
угловых скоростей показываем на рисунке
в виде векторов (рис. П.10).
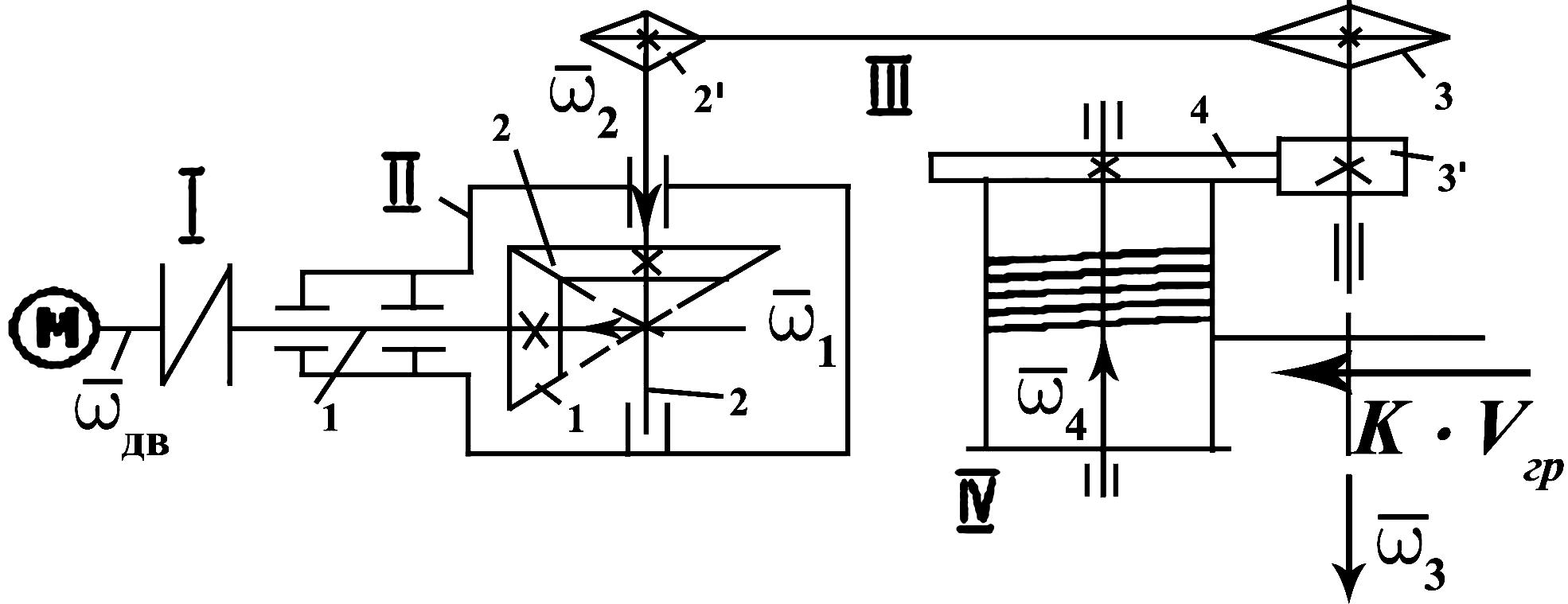
Рис.
П.10
Методические
указания к решению задач К-5 и К-6
Задачи
К-5 и К-6 относятся к теме «Кинематика
плоскопараллельного движения твердого
тела». Для их решения необходимо изучить
вопросы:
-
мгновенный
центр скоростей тела (МЦС); -
способы
нахождения положения МЦС тела в
зависимости от имеющейся информации
о движении тела и его точек; -
способы
определения скоростей точек тела и его
угловой скорости с использованием МЦС.
Особое внимание
следует обратить на зависимость скоростей
точек тела от взаимного положения этих
точек и МЦС тела. Для упрощения вычислений
может оказаться полезным известное
свойство пропорций.
Если
,
то
Кратность полиспаста
может быть вычислена кинематическим
способом, как отношение скорости
свободного конца троса к скорости
подъема груза. При этом считается
(дополнительно к условию задачи), что
трос не проскальзывает относительно
блоков и является идеально гибким и
нерастяжим. С учетом этих оговорок надо
последовательно рассмотреть движение
каждого блока в отдельности.
Для решения задачи
К6 необходимо выполнить в масштабе две
проекции механизма – заданную схему и
вид вдоль геометрической оси центральных
колес. На этом втором виде следует
показать (в масштабе) векторы скоростей
характерных точек (оси сателлита, точек
зацепления колес) и угловые скорости
всех тел.
Пример
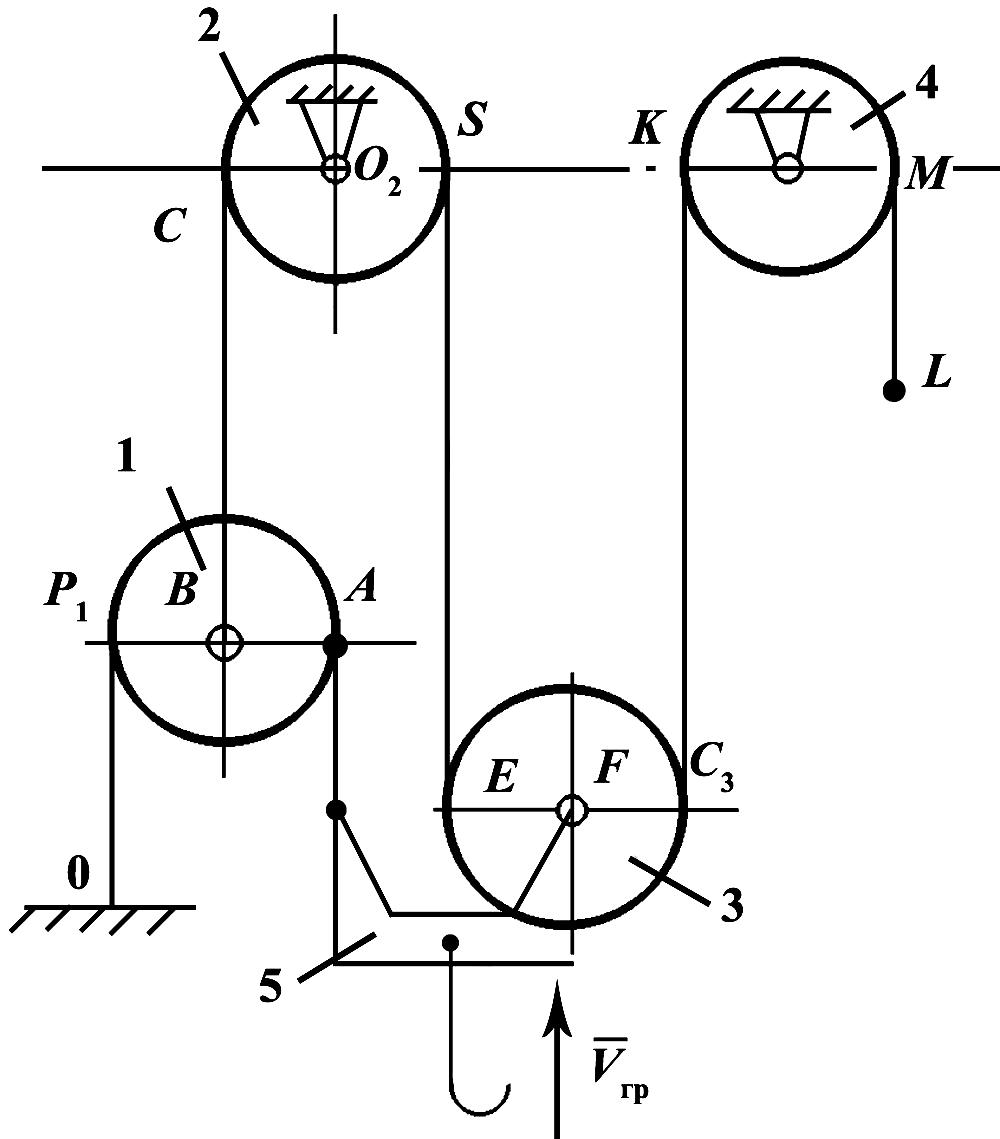
7
Дано:
скорость подъема груза Vгр
= 0,5 м/с, радиусы всех блоков одинаковы
и равны 5 см.
Произвести
кинематический расчёт полиспаста.
|
|
|
|
Рис. |
П.12 |
Решение
В данной системе
блоки 2 и 4 вращаются вокруг неподвижных
осей.
По принятой
терминологии они называются неподвижными.
Блоки 1 и 3 – подвижные. Подвижная траверса
5 движется поступательно со скоростью
Vгр.
Рассмотрим последовательно движение
каждого блока.
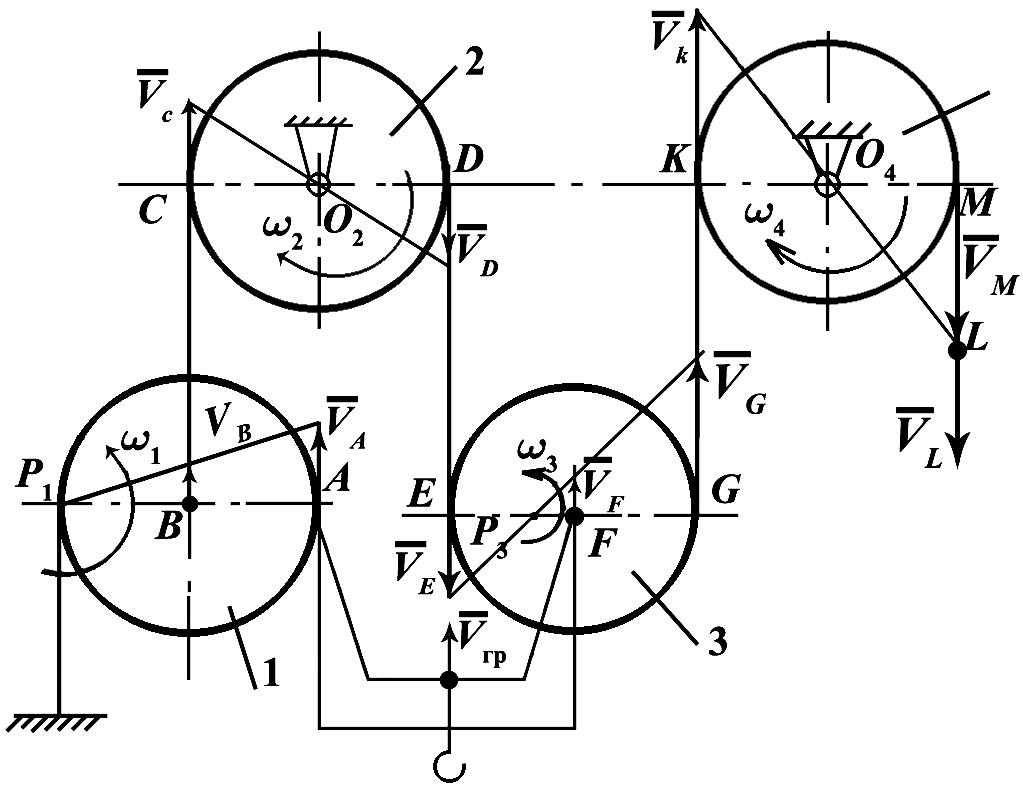
Рис.
П.13
Блок 1 (рис. П.14, а)
совершает плоскопараллельное движение.
Точка Р1
является его МЦС. Точка А
имеет скорость VА
= Vгр
= 0,5 м/с. Угловая скорость блока 1:

Отсюда:
С такой скоростью
движутся все точки участка ВС
троса (рис. 13).
Блок 2 (рис. 14, б)
вращается вокруг неподвижной оси О2
с угловой скоростью

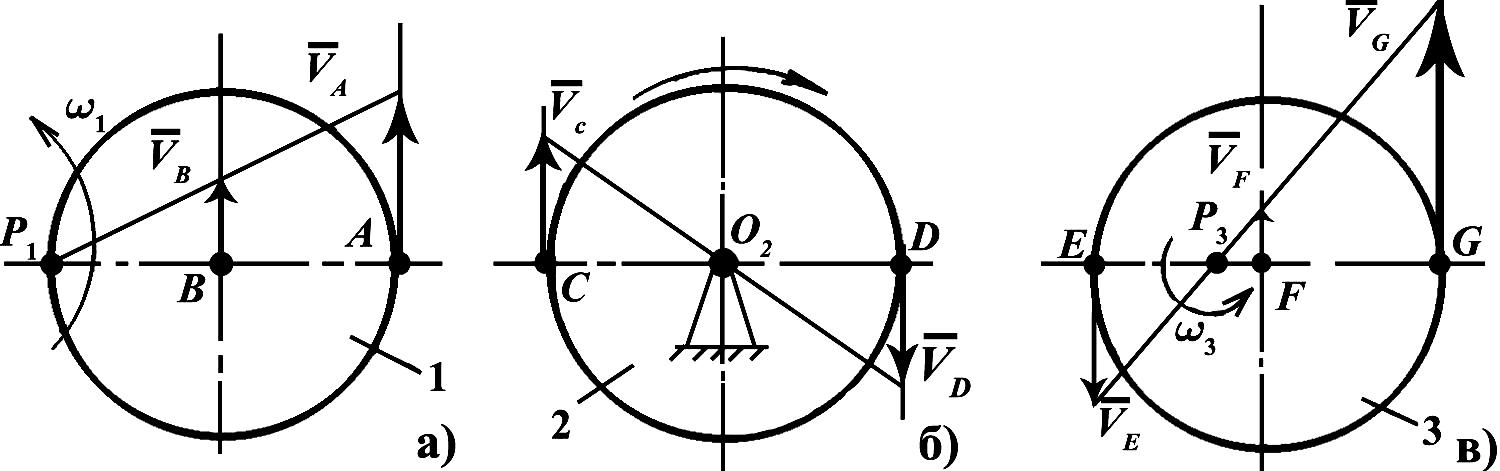
Рис. П.14
Скорость точки D
(рис.П.13 и
П.14, б): VD
= VC
= 0,25 м/с.
Эта скорость
передается точке Е
блока 3 (рис. П.13 и П.14, в).
Блок 3 совершает
плоскопараллельное движение и при этом
VЕ
= VD
= 0,25 м/с; VF
= Vгр
= 0, 5 м/с.
Построением находим
МЦС блока 3 – точку Р3.
Определяем направление угловой скорости
и затем вычисляем ее величину и расстояние
Р3F
,уточняющее положение МЦС блока 3:
рад/с;
м.
Тогда (рис. П.14, в):
м.
и скорость точки
G:
м/с.
Блок 4 (рис. П.13)
вращается вокруг неподвижной оси О4.
Его точке К
передается скорость точки G:
м/с.
С такой же скоростью
движется точка М
блока и свободный конец троса:
м/с, а угловая скорость блока 4
рад/с.
Кратность полиспаста
.
Показываем на
рисунке в картину движения системы, т.
е. направления угловых скоростей блоков,
положения МЦС «подвижных» блоков,
скорости характерных точек – центров
блоков, точек схода троса с блоков и
набегания его на них.
Пример
8
Дано: r1=
7см; r2=
10 см;
см; 1
= 20 рад/с; 1
= – 3 рад/с.
Произвести
кинематический расчет механизма (рис.
П.15, а).
Рис. П.15, а
Рис.
П.15, б
Определить угловые
скорости всех звеньев механизма и
показать их направления.
Решение
Данный механизм
является дифференциальным, т. к. у него
нет неподвижного центрального колеса.
Выполняем в масштабе с учетом заданных
линейных размеров два вида кинематической
схемы механизма – исходную и вид вдоль
оси вращения центральных колес (рис.
П.15 а, б). На обоих видах отмечаем
характерные точки, показываем в виде
векторов и круговых стрелок направления
заданных угловых скоростей тел 1
и 3
(центральное колесо 1 и водило 3 вращаются
в разные стороны). В дальнейшем знаки
угловых скоростей игнорируем и по мере
вычисления величин показываем на
дополнительном рисунке (вид вдоль осей
вращения) истинные направления вращения
колес и векторы скоростей точек.
Имеем:
точка А1
принадлежит центральному колесу 1,
вращающемуся с угловой скоростью 1
вокруг неподвижной оси. Поэтому:
см/с.
На рисунках точка
А1
совпадает с точкой А.
Точка С3
(на оси сателлита) принадлежит водилу
3 вращающемуся вокруг неподвижной оси,
совпадающей с осью центральных колес.
Поэтому
,
где
(рис. П.15, а).
Получаем:
см;
см/с.
С
точками А1
и С3
совпадают точки А2
и С2
сателлита (блока колес 2 – 2).
Их скорости
векторно равны скоростям точек А1
и С3
соответственно:
;
.
Зная величины и
направления скоростей двух точек
сателлита (блока колес 2 – 2),
можно найти положение МЦС этого тела
(рис. П.16).
Угловая скорость
блока 2 – 2:

Рис. П.16
,
или
рад/с;
м.
Следовательно,
см;
см/с.
Точка В
является точкой зацепления колес 2
и 4. Так как колеса не проскальзывают
относительно друг друга, а колесо 4
вращается вокруг неподвижной оси, то
рад/с (по часовой стрелке).
Радиус колеса 4 по
рис. П.15, а:
см.
Итак, кинематический
расчет дифференциального механизма
выполнен, угловая скорость и направления
вращения всех звеньев механизма найдены.
Результаты расчетов (картина движения)
показаны на рис. П.15, б.
Методические
указания к решению задач К-7, К-8, К-13
Эти
задачи посвящены изучению кинематики
плоских рычажных механизмов. Звенья
таких механизмов совершают либо
простейшие движения (поступательное,
вращательное вокруг неподвижной оси),
либо – плоскопараллельное. Считается,
что механизм расположен в плоскости
рисунка и все его звенья и точки движутся
в этой же плоскости.
Приступая
к решению задачи, необходимо уточнить,
какое именно движение совершает каждое
звено механизма. При выполнении такого
анализа легко установить, что каждая
подвижная точка механизма, выделенная
на рисунке кинематической схемы,
принадлежит одновременно двум звеньям
и одно из них совершает плоскопараллельное
движение. Через эти точки, общие для
двух звеньев, передаётся движение от
одного из них к другому.
Каждую
из задач можно рассматривать, как
состоящую из двух частей: 1 – определение
скоростей и 2 – определение ускорений.
В решении этих частей есть много общего,
хотя они существенно различаются по
сложности и применяемым способам. Общим
здесь является то, что как при определении
скоростей, так и при определении
ускорений, приходится последовательно
переходить от рассмотрения движения
одного тела к изучению движения другого,
а от него – к следующему и т. д. Такие
переходы можно осуществить зная скорость
(или соответственно ускорение) той
точки, которая является общей для
рассматриваемой пары тел. Эта
последовательность решения задач вполне
естественна, поскольку в самих механизмах
передача движений от одного звена к
другому осуществляется именно аналогичным
путём.
Общим
в решении задач по определению скоростей
и ускорений является то, что скорости
(ускорения) любых двух точек А
и В
одного и того же тела не могут быть
произвольными и связаны при его
плоскопараллельном движении векторными
зависимостями
(а)
(б)
эти
выражения соответствуют представлению
плоскопараллельного движения тела в
виде суммы двух одновременно происходящих
простейших движений: поступательного
со скоростью
(или
ускорением
)
точки А,
принимаемой за полюс, и вращательного
движения тела вокруг этого полюса.
Обычно
в качестве полюса принимается такая
точка тела, скорость (или соответственно
ускорение) которой уже известна из
предыдущего решения.
Различия
же в определении скоростей и ускорений
происходят из-за того, что направления
векторов ускорений в отличие от
направлений векторов скоростей
предсказать заранее практически
невозможно. Если учесть, что при вращении
тела вокруг полюса А
ускорение
складывается из нормальной и касательной
составляющих, а полное ускорение точки
В,
движущейся по криволинейной траектории,
состоит из аналогичных частей, то
исходная формула (б) принимает вид:
, (в)
а формула для
скорости остаётся неизменной:
(а)
Направление
и (или) величина каждого из векторов,
входящих в (а) или (в), могут быть заранее
известны либо неизвестны. При большом
количестве (более двух) таких неизвестных
в одном векторном уравнении оно не может
быть решено никакими приёмами.
Подобная
ситуация чаще возникает при определении
ускорений, но чтобы убедиться в возможности
решить векторное уравнение для определения
скоростей (или ускорений), необходимо
производить предварительный анализ
каждого уравнения. Такие анализы
приведены в примерах решения задач.
Лишь
после того, как будет выяснено, что
записанное векторное уравнение может
быть решено, приступают непосредственно
к его решению.
Для
определения ускорений с помощью формул
типа (в) можно рекомендовать аналитический
метод: метод проецирования решаемого
векторного уравнения на произвольно
принимаемые оси координат. Существуют
и другие способы (например, графический
способ – путём построения плана
ускорений).
Решение векторных
уравнений типа (а) с небольшим количеством
векторов, входящих в него, можно
осуществить и аналитически, и графически,
и графоаналитическим способом.
Проецированием
уравнения (а) на прямую АВ
получается выражение:
, (г),
называемое
теоремой о проекциях скоростей двух
точек твёрдого тела на прямую, соединяющую
их, или основной теоремой кинематики
твёрдого тела.
Оно
выполняется при любом движении любого
твёрдого тела (т. к. для такого тела
всегда
).
Существует
и наглядная интерпретация плоскопараллельного
движения тела: в каждый момент времени
это движение можно рассматривать как
вращение тела вокруг МЦС (только с точки
зрения распределения скоростей точек
тела). Поэтому скорости точек тела могут
быть успешно и с большой наглядностью
определены с помощью МЦС.
Методические
указания к решению задач К-9, К-10, К-11,
К-12.
При
решении задач на тему «Сложное движение
точки» необходимо предварительно чётко
установить, какое движение точки является
относительным, абсолютным и переносным,
как они происходят (в чём они заключаются),
затем определить положение тела и точки
на нём в заданный момент времени t1
и выполнить соответствующий рисунок
схемы.
При
определении скоростей точки в любом из
движений (в переносном, относительном,
абсолютном) применяется теорема о
сложении скоростей:
,
а при определении ускорений – теорема
Кориолиса о сложении ускорений:
.
В
случае поступательного переносного
движения Кориолисово ускорение
отсутствует и ускорение точки определяется
по формуле:
.
Рекомендуется
решать подобные векторные уравнения
аналитически, путём проецирования их
на принятые оси координат. В тех случаях,
когда слагаемые векторы расположены в
одной плоскости (например, в плоскости
рисунка) при их решении могут быть
использованы другие способы (графические,
графоаналитические). Следует иметь в
виду, что векторные уравнения данного
типа (когда векторы расположены в одной
плоскости, например, в плоскости рисунка)
могут быть решены только в том случае,
если количество неизвестных не превышает
двух. При этом к неизвестным следует
относить и модуль и направление любого
из векторов.
Пример
9
Механизм
состоит из стержней 1, 2, 3, 4 и ползуна В,
соединённых друг с другом и с неподвижными
опорами О1
и О4
шарнирами.
Дано:
= 60,
= 150,
= 90,
= 30,
AD
= DB,
l1
= 0,4 м;
l2
= 1,2 м,
l3
= 1,4 м,
l4
= 0,6 м.
1
= 2с – 1,
1
= 7с – 2
(направления
1
и 1
против хода
часовой стрелки).
Определить:
VB,
VE,
2,
,
2.
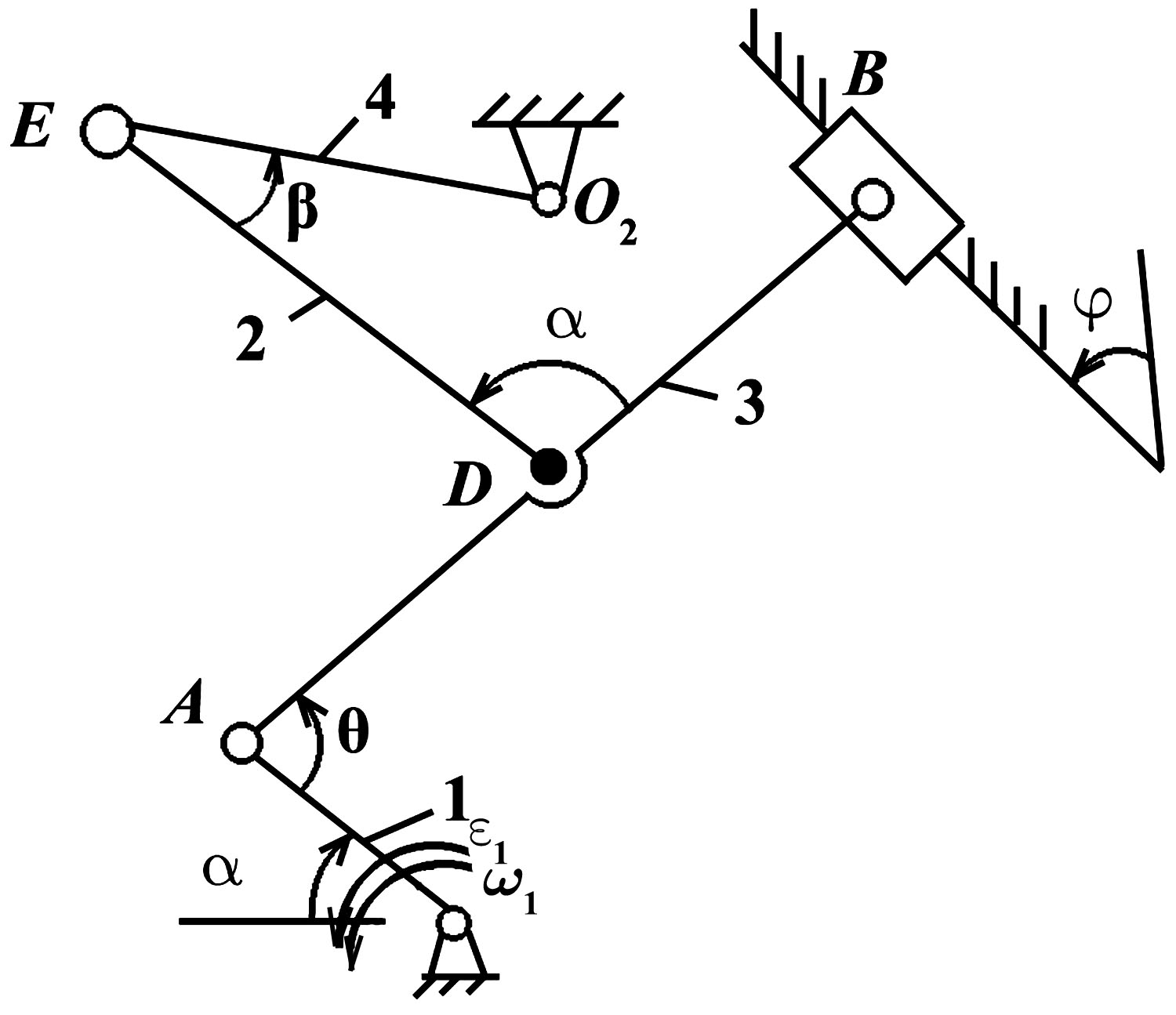
Рис.
П.17
Решение
Выполняем
рисунок схемы механизма в заданном
положении в соответствии с исходными
данными (рис. П.18)
Рис.
П.18
Определение
скоростей
Скорость
точки А.
Эта точка принадлежит телу 1, вращающемуся
с угловой скоростью 1
вокруг О1,
поэтому
Вектор
и направлен в сторону вращения.
Точка
А
одновременно принадлежит и телу 3,
которое совершает плоскопараллельное
движение. Так как известна траектория
точки В
тела 3, то можно определить скорость
этой точки. Для этого воспользуемся
понятием МЦС. Чтобы найти положение МЦС
тела 3, восстановим перпендикуляры к
направлениям скоростей точек А
и В
этого тела. На их пересечении получим
точку Р3
– МЦС тела 3. Вокруг неё в данный момент
времени происходит поворот тела 3 с
угловой скоростью 3.
Направление 3
находим, пользуясь известным направлением
:
звено 3 вращается против хода часовой
стрелки. Следовательно,
и направлен в сторону вращения тела 3
(вверх по направляющей).
Вычисляем
величины 3
и VВ.
Из
полученного
(он прямоугольный) находим:
м;
м.
Так
как по свойству скоростей точек тела,
совершающего плоскопараллельное
движение
,
то
;
;
,
из
– он равносторонний из построения.
Показываем
на рисунке найденные скорости. Для
нахождения скорости точки Е учтём, что
она одновременно принадлежит и телу 2,
и телу 4, причём, т.к. тело 4 вращается
вокруг неподвижной оси О4,
то скорость
и
Найдём
МЦС тела 2 – точку Р2
(на пересечении перпендикуляров к
скоростям точек D
и Е).
По известной величине и направлению
находим угловую скорость 2:
(по
ходу часовой стрелки)
Р2D
из
DP2E
равно
Тогда
.
Из
P2ED
P2E
= P2D
т. к.
P2DE
равнобедренный. VE
= 0,46 м/с
Полученные
результаты расчёта показываем на рисунке
Определим
4:
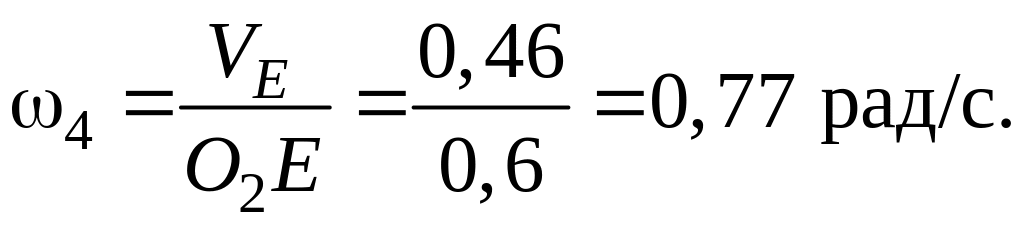
4
направлено против хода часовой стрелки
в соответствии с направлением VE.
Определение
ускорений
По
заданному движению тела 1 находим
ускорение точки А.
Так как тело 1 вращается вокруг неподвижной
оси О1,
то
где
(О1А
– влево);
(вдоль А1О
к точке О1)
Показываем
эти векторы на рис. П.20.
Для
определения ускорения
воспользуемся тем, что точка В
принадлежит телу 3, совершающему
плоскопараллельное движение. Этому
телу принадлежит и точка А,
ускорение которой уже найдено. Поэтому
её (точку А)
можно принять за полюс и записать для
или
учитывая, что
,
получаем:
|
= |
+ |
+ |
+ |
|
|
|
величина вектора |
неизв. |
|
|
|
|
|
направление вектора |
направлен |
изв. |
изв. |
по |
АВ |
Здесь
векторная формула дополнена таблицей
анализа величины и направления каждого
из векторов, входящих в формулу.
Направление
вектора
показываем по перпендикуляру к АВ
предположительно (рис. П.19), после решения
уравнения уточним это направление.
Проводим
оси координат и проецируем векторное
уравнение на оси X
и Y.
Проецируя
уравнение на ось X,
получаем
откуда
находим:
Так
как
,
то вектор
направлен так, как показано на рисунке.
Проецируя
уравнение на ось
Y,
получаем:
.
Подставляя
числовые значения, вычисляем
.
Знак
(–) показывает, что вектор
имеет направление, противоположное
показанному на рис. П.19.
Находим
3

Показываем
истинное направление 3
на рисунке
с учётом полученного знака у вектора
(рис. П.20).
|
|
|
|
Рис. |
Рис. |
Пример
10
Шток
2, движущийся в прямолинейных направляющих
своим концом К
скользит по поверхности круглого
эксцентрика (диска) и толкая его приводит
последний во вращательное движение
вокруг неподвижной оси. Шток 2 и эксцентрик
1 расположены и движутся в плоскости
рисунка, а ось вращения эксцентрика
перпендикулярна этой плоскости.
Дано:
Определить:
1,
1
в этот момент времени

Рис.
П.21
Решение
По
условию задачи задано движение штока
2. С этой скоростью и ускорением движется
и острие К
штока относительно неподвижной системы
отсчёта. Но перемещение штока приводит
к повороту эксцентрика 1 вокруг оси О1.
При этом острие К
штока скользит по криволинейной
поверхности эксцентрика, т. е. совершает
движение относительно движущегося
тела. В соответствии с определениями
понятий «сложное, абсолютное, относительное
и переносное движение точки» можно
говорить о сложном движении острия К:
вращающийся эксцентрик – подвижная
система отсчёта, а его движение –
переносное движение для острия.
По
теореме о сложении скоростей точки,
совершающей сложное движение, можно
записать для точки К
штока:
Рис.
П.22
Проведём анализ
векторного равенства
|
|
|
|
|
|
величина |
известна |
|
? |
|
направление |
известно |
|
По |
Выбирая
оси X
и Y,
проектируем на них это векторное
уравнение.
-
на
ось X:
; -
на
ось Y:
.
Учитывая,
что в данном положении системы (при
)
угол
,
решаем полученную систему уравнений и
находим
Следовательно,

Направление
показано на рис. П.22. Оно определяется
направлением вектора
,
которое получается при разложении
вектора
на составляющие.
Для
определения ускорений воспользуемся
теоремой Кориолиса, предварительно
определив величину и направление вектора
Кориолисова ускорения острия штока.
Поскольку оба составных движения этой
точки происходят в плоскости рисунка,
то направление
находим по правилу Н.
Е.
Жуковского,
повернув вектор
на 90
в сторону переносного вращения. Величина
ускорения Кориолиса в этом случае
находится по формуле:
По
теореме Кориолиса для точки К
имеем:
.
Но
так как переносное движение – вращательное,
а относительное происходит по криволинейной
траектории, то ускорение точки К
в каждом из этих движений складывается
из касательной и нормальной составляющих:
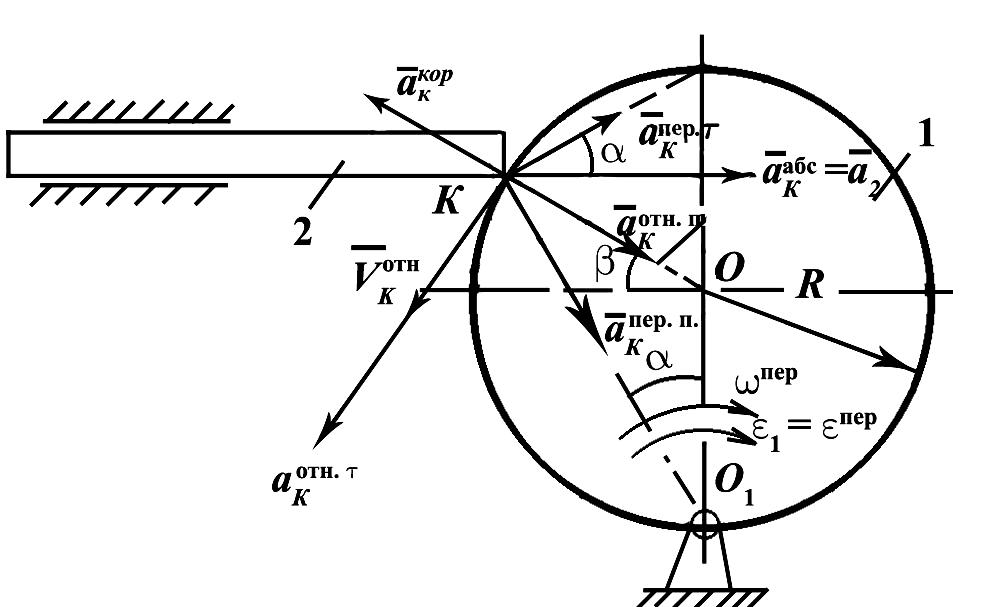
Рис.
П.23
Проведём
анализ векторного равенства
,
и его результат оформим в виде таблицы:
|
|
|
|
|
|
|
|
|
величина |
известна |
|
|
? |
|
извес. |
|
направление |
известно |
О1К |
к |
|
к точке О |
ивест. |
Проекции
этого уравнения на оси X
и Y
приводят к системе:
Решение её даёт:
;
Знаки
«–» указывают на то, что принятые ранее
направления векторов
и
оказались неверными и в действительности
эти векторы направлены противоположно
показанным на рисунке.
Угловое ускорение
эксцентрика:
,
т. е.
и
направлено против хода часовой стрелки.
Вращение эксцентрика в данный момент
времени происходит замедленно, т.
к. направления
1
и 1
противоположны.
Пример
11
Точка
М
движется по поверхности тела D
по закону
Определить
абсолютную скорость и абсолютное
ускорение точки М
при
,
если тело D
приводится в движение вращением кривошипа
О1А
по закону
рад. На
рисунке показано положение точки М,
соответствующее
.
А
Рис.
П.24
Дано:
см,
см.
Решение
Точка
М
совершает сложное движение, т. к. она
перемещается по поверхности движущегося
тела D.
Движение тела D
является для точки М
переносным. Особенности механизма и
его размеры таковы, что тело D
движется поступательно и каждая его
точка описывает окружность одного и
того же радиуса
,
но центры их для каждой точки тела
D-свои,
не совпадающие, ни с точкой O1
ни с точкой O2.
Движение точки М
по поверхности тела D
– относительное.
Оно происходит по заданному закону
вдоль криволинейной траектории радиуса
R
с центром в точке О.
Уточним
положения тела D
и точки М
в заданный момент времени. Положение
тела D
относительно неподвижной прямой O1O2
определяется углом .
При t1
=
1
c
рад.
Положение
точки М
на полуокружности ACB
определяется дугой.
см.
Это соответствует
центральному углу
Выполняем
рисунок, соответствующий этим положениям
точки М
и тела D
(рис. П.25).
Рис.
П.25
Определяем
абсолютную скорость точки М
по формуле:
Относительная
скорость точки:
при t1
=
1
c
Vотн
=
7,58
см/с.
Положительный знак Vотн
показывает, что относительное движение
точки происходит в положительном
направлении. Вектор
направлен
по касательной к траектории относительного
движения, т. е. по касательной к дуге
окружности радиуса R
в положении М1.
Переносная
скорость той точки тела D,
с которой совпадает в момент времени
t1
c
точкой M1,
но, т.
к. тело D
движется поступательно, то все его точки
в каждый момент времени имеют одинаковые
скорости и ускорения:
они соответственно равны скорости и
ускорению точки А.
Итак:
,
где
– модуль угловой скорости звена О1А.
Находим
:
рад/с, при t1
=
1
c,
=
рад/c.
Показываем направление
на рисунке с учётом полученного знака
(+), показывающего, что вращение звена
О1А
происходит в направлении возрастания
угла .
Модуль
переносной скорости
.
Вектор
направлен
в сторону вращения звена
.
Модуль
абсолютной скорости точки М
можно найти аналитически, т. е. способом
проекций. Показываем на рисунке
направление осей координат.

Абсолютную
скорость точки М
можно найти и по теореме косинусов, т.
е. графоаналитическим.
Определяем
ускорение точки М.
Так
как
движение
тела Д
поступательное, то абсолютное ускорение
точки М
находится по формуле:
Относительное
движение точки –
криволинейное, поэтому
Переносное
ускорение точки М
в данный момент времени – ускорение
точки тела D
движущегося поступательно. Ускорения
всех его точек одинаковы и равны,
например, ускорению точки A.
Величина и
направление
одинаковы с ускорением точки А
.
Расчетная
формула принимает вид:
.
Вычислим
модули всех векторов и покажем их
направление на рисунке
,
при
t1
=
1
c
Знаки
и
при t1
=
1
c
разные, т. е. относительное движение
замедленное (векторы
и
направлены противоположно друг другу)
;
при
t1
=
1
c;

Рис.
П.26
Вектор
направлен перпендикулярно
к центру кривизны траектории относительного
движения, т. е. к точке С.
При
поступательном переносном движении
переносное ускорение точки М
совпадает с ускорением любой точки тела
Д,
например, точки А.
Поэтому
;
при
t1
= 1 c
Вектор
направлен вертикально вниз (
)
;
Так
как знаки
и
одинаковы, то вращение звена О1А
– ускоренное.
20=62,8
см/с2.
Вектор
направлен перпендикулярно О1А,
т. е. влево. Показываем векторы ускорений
на рис. П.26.
Модуль
абсолютного ускорения находим способом
проекций, проецируя выражения
на принятые оси координат X
и Y:
;
при
t1
= 1 c
;
;
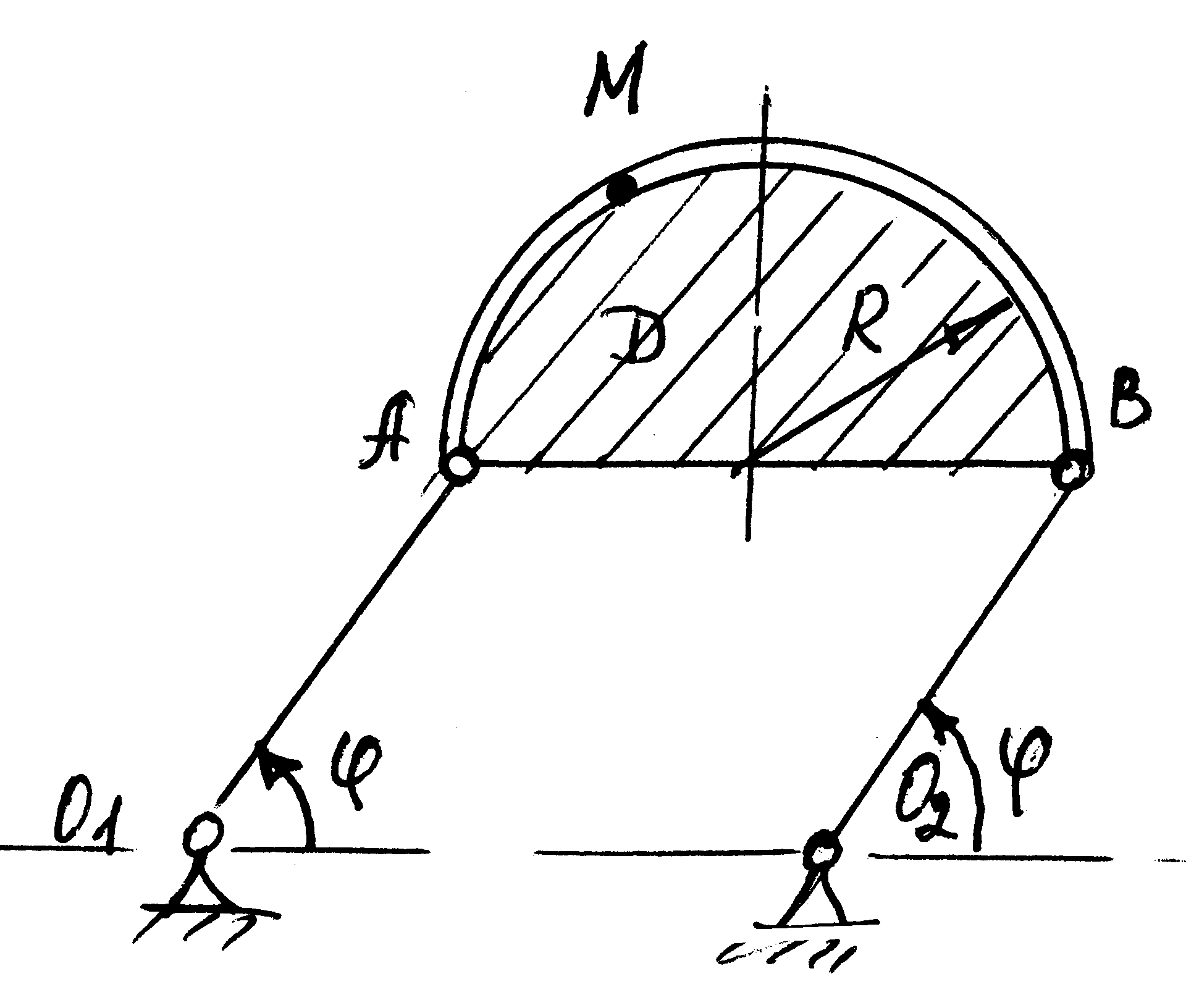
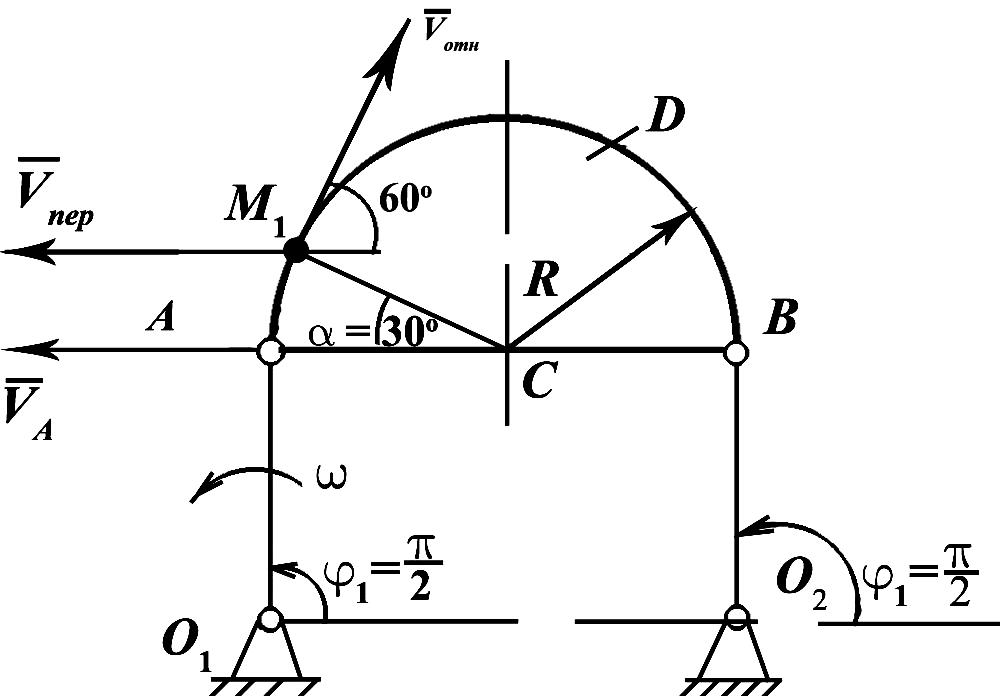
Пример
12
Треугольная
пластина ADE
вращается вокруг оси Z
с угловой скоростью
(положительное направление
показано на рисунке дуговой стрелкой).
По гипотенузе AD
движется точка В
по закону
(положительное направление отсчёта S
от А
к D).
Определить абсолютную скорость
и абсолютное ускорение
точки B
в момент времени t1
= 2 c.
|
Рис. |
Решение
Движение .
Вычислим в момент времени t1
Знак направлен в сторону отсчёта положительных |
Переносное
движение – это вращение пластины с
угловой скоростью .
Найдём
угловую скорость и угловое ускорение
переносного вращения.
;
.
При
t1
= 2 c;
= –1 c–1;
= 1,2с–2
знаки показывают что в момент времени
t1
= 2 c
направление
противоположно показанному на рис. П.28
и вращение в этот момент замедленное.
Определим
положение точки В
в момент времени t1
= 2 c:
S1
= AB1
= 20 см.
Находим
по рис. П.28 расстояние h1
точки В1
от оси вращения:
h1
= AB1sin30
= 10 см.
Находим
Vпер
Вектор
направлен перпендикулярно h1
в сторону переносного вращения, т. е. по
оси X
неподвижных
осей координат, проведенных через точку
О.
|
Для необходимо сложить векторы и , в момент времени t1
Абсолютное
Так .
Относительное |
Рис. |
Расчётная
формула для определения
принимает вид:
.
Вычислим
и величины и уточним направление всех
векторов , входящие в эту формулу.
|
Находим
Направление к точке А.
Находим и
Вектор в плоскости рисунка перпендикулярен |
Рис. |
Вектор
перпендикулярен О1В1.
Вектор
угловой скорости
переносного вращения и вектор
образуют угол
= 30,
поэтому модуль Кориолисова ускорения
определится как
.
Направление
можно найти по правилу векторного
произведения:
,
или
правилу Н. Е. Жуковского. Для этого вектор
спроецируем в плоскость, перпендикулярную
оси вращения и затем эту проекцию
повернём на 90
в сторону ,
т. е. по ходу часовой стрелки. Таким
образом, получим направление
.
Он направлен перпендикулярно плоскости
пластины, т. е. в направлении оси X.
Для
определения
воспользуемся осями, проведёнными через
точку О.
Проектируя
равенство
на оси X,
Y,
Z
находим проекции
на эти оси:
;
;
.
Находим
значение
:
Пример
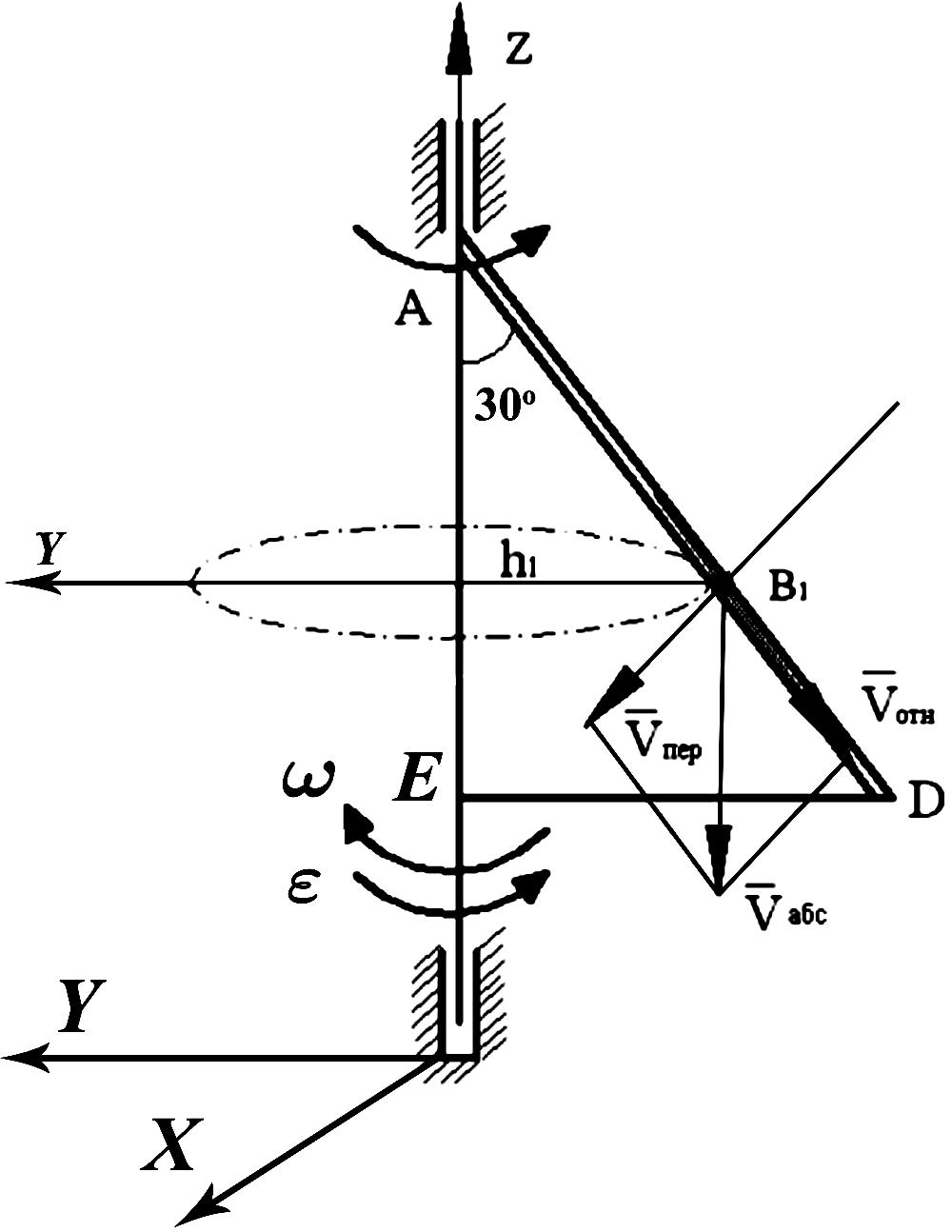
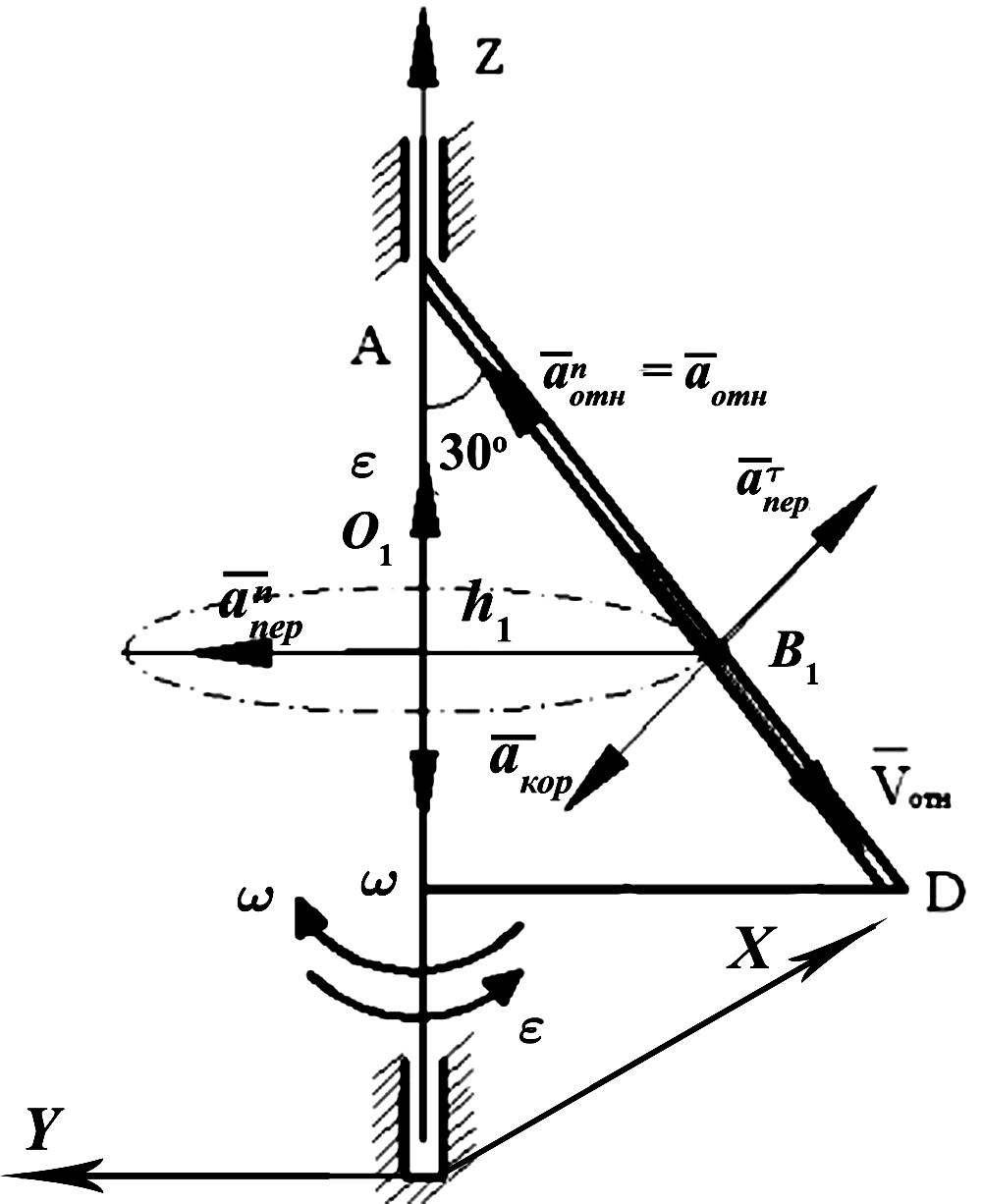
13
Тело
произвольной формы вращается вокруг
оси, проходящей через точку О
перпендикулярно плоскости пластины с
угловой скоростью
(положительное
направление отсчёта
показано на рис. П.30).
По дуге окружности радиуса R
= 0,5 м движется точка В
по закону
,
t
– сек. (положительные отсчёты от А
к В).
Определить абсолютную скорость и
абсолютное ускорение точки в момент
времени t1
= 2 c.
Решение
Рассмотрим
сложное движение точки В.
Вращение пластины с угловой скоростью
= 2t
– 1,5t2
является переносным движением точки.
Угловая скорость переносного движения
определится при t1
= 2 c
1пер
= 4 – 1,54
= – 2 с–2.
Знак
(–) показывает, что направление 1
противоположно показанному на рис. П.30
Рис.
П.30
Угловое
ускорение переносного движения
определится
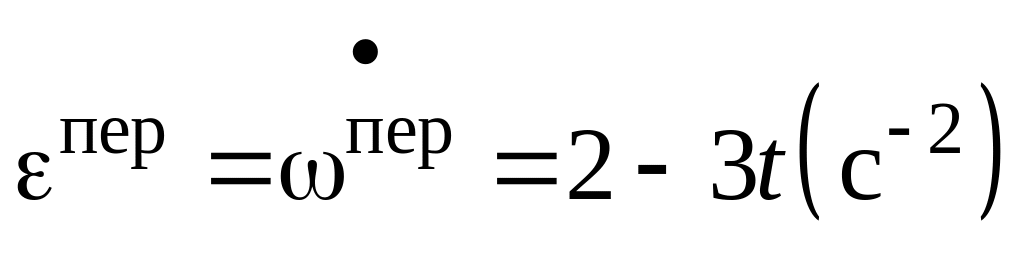
при
t1
= 2 c
Показываем
направление пер
и пер
на рисунке с учётом полученных знаков.
Абсолютная
скорость точки
находится по формуле:
Определяем величины,
входящие в это равенство.
Относительное
движение точки происходит по закону
Устанавливаем,
где будет находиться точка В
на дуге окружности в момент времени t1.
R(м)
Тогда
(рад)
Знак
(–) свидетельствует о том, что точка В
в момент времени t1
= 2 с находится справа от точки А.
Показываем её положение на рис. П.31
(точка В1).
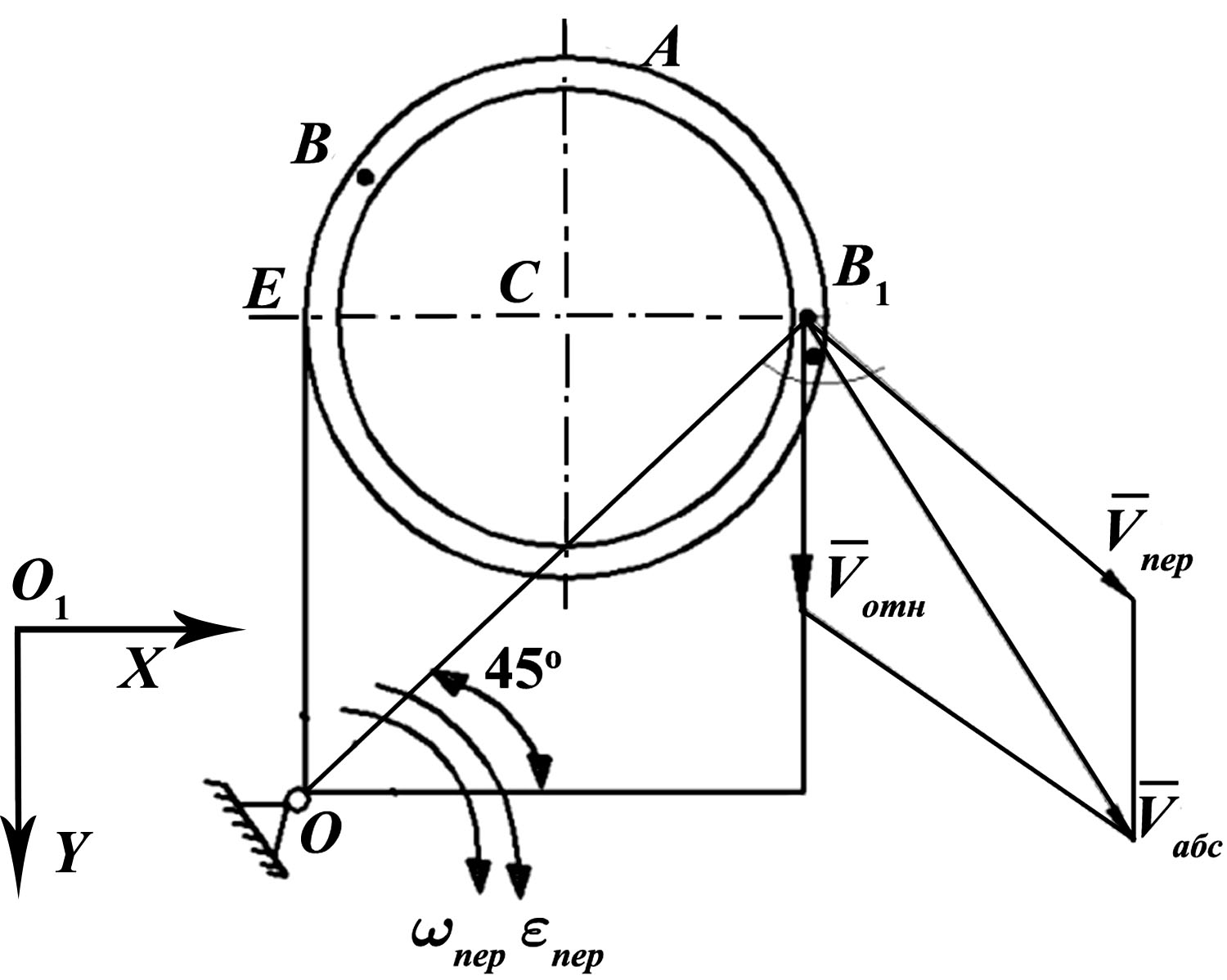
Рис.
П.31
Находим
числовые значения
и
;
,
где
в момент времени t1
= 2 c.
,
Показываем
направление векторов
и
с учётом полученных знаков на рис. П.31.
Вектор
направлен
расстоянию ОВ1
в сторону переносного вращения, вектор
направлен по касательной к траектории
относительного движения в сторону,
противоположную положительному отсчёту
дуговой координаты S,
т. к. в расчёте получен знак (–).
Проведём
координатные оси О1XY
и спроектируем обе части равенства,
определяющего
на оси.
На
ось Х:
На
ось Y:
Находим
.
Абсолютное
ускорение точки В1
определим по формуле:
Переносное
движение – это вращение пластины вокруг
точки О,
поэтому
Относительное
движение точки В1
– криволинейное движение по окружности
радиуса R
пластины, поэтому
Расчётная
формула для определения
принимает вид:
Определим
модуль и направление всех векторов,
входящих в это равенство (рис. П.32).
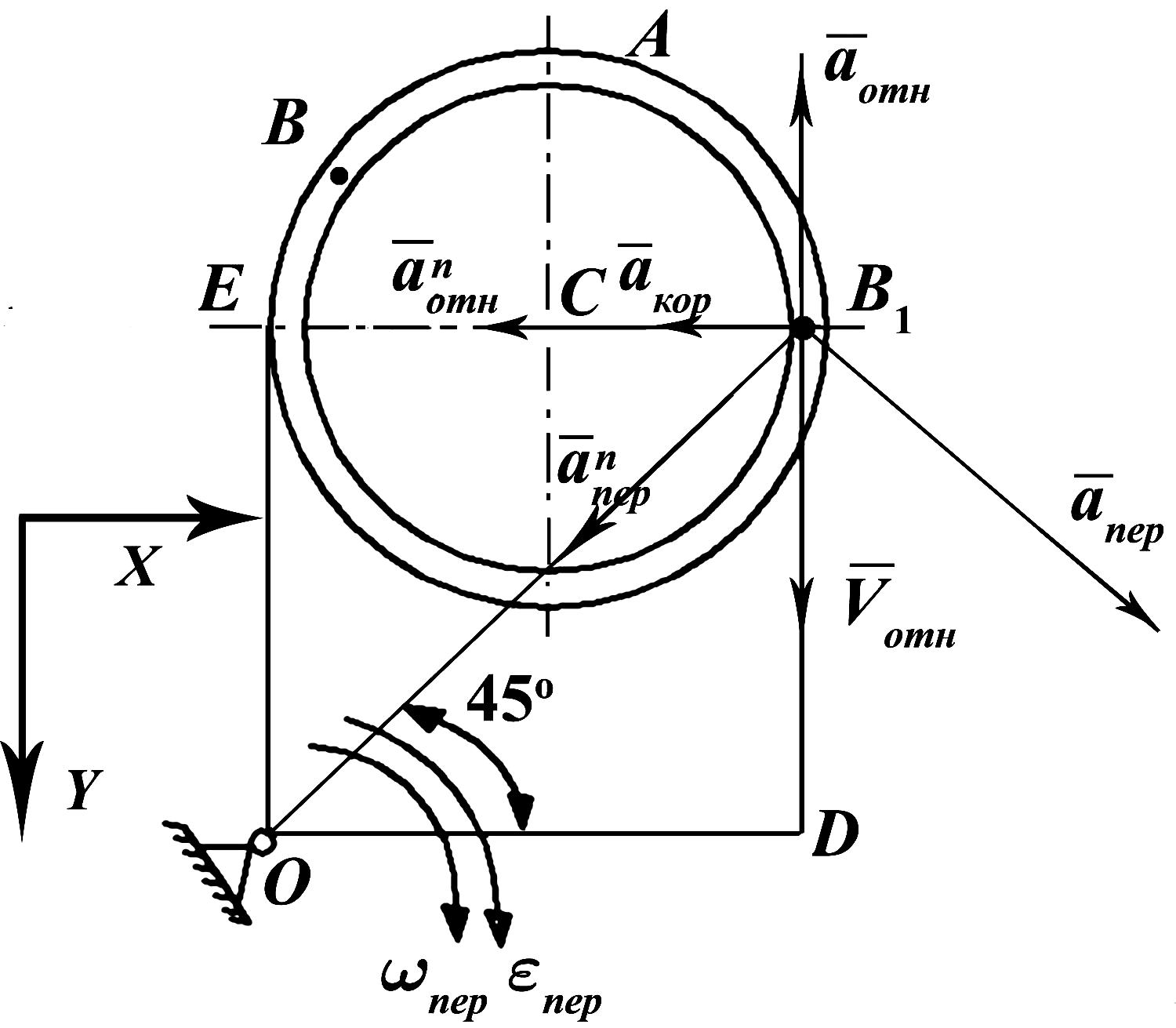
Рис.
П.32
Вектор
направлен
по прямой В1О
к центру вращения О.
.
Вектор
направлен перпендикулярно ОВ1
в сторону
.

при
t1
= 2 c,
,
,
где отн
– радиус кривизны траектории точки в
относительном движении.
отн
= R.
Вектор
направлен
перпендикулярно
в сторону вогнутости траектории.
Вектор
направлен противоположно вектору
,
т. к. знаки
и
противоположны.
Находим
Кориолисово ускорение
.
Модуль
Кориолисова ускорения определяем по
формуле:
,
где
– угол между векторами
и
.
Вектор
направлен вдоль оси вращения пластины
перпендикулярно к плоскости чертежа,
т. е. перпендикулярен вектору
,
лежащему в плоскости пластины, значит,
= 90.
Вычисляем
при t1
= 2 c.
Направление
найдём по правилу Н. Е. Жуковского,
поворотом вектора
на 90
в сторону пер.
Таким
образом, значения всех входящих в правые
части равенства
векторов и их направления найдены. Для
сложения этих векторов проводим оси
координат и спроектируем обе части
равенства, определяющего
,
на эти оси.
На
ось Х:
.
На
ось Y:
.
Подставляя
числовые значения для момента времени
t1
= 2 c
находим:
аабсX
=
– 9,74 м/с2,
Пример
14
Простейший
рычажный механизм с двумя степенями
свободы представляет собой два шарнирно
соединённых стержня, свободные концы
которых скользят по общей горизонтальной
направляющей. Механизм расположен в
плоскости рисунка (рис. П.33). Определить
,
если
;
,
их
направления показаны на рисунке. При
вычислениях принять: АС
= 0,8 м, ВС
= 0,6 м и в рассматриваемый момент cos
= 0,8, cos
= 0,6.

Рис.
П.33
Решение
Для
определения
воспользуемся
теоремой о проекциях скоростей и применим
её отдельно к телу 1 и телу 2.
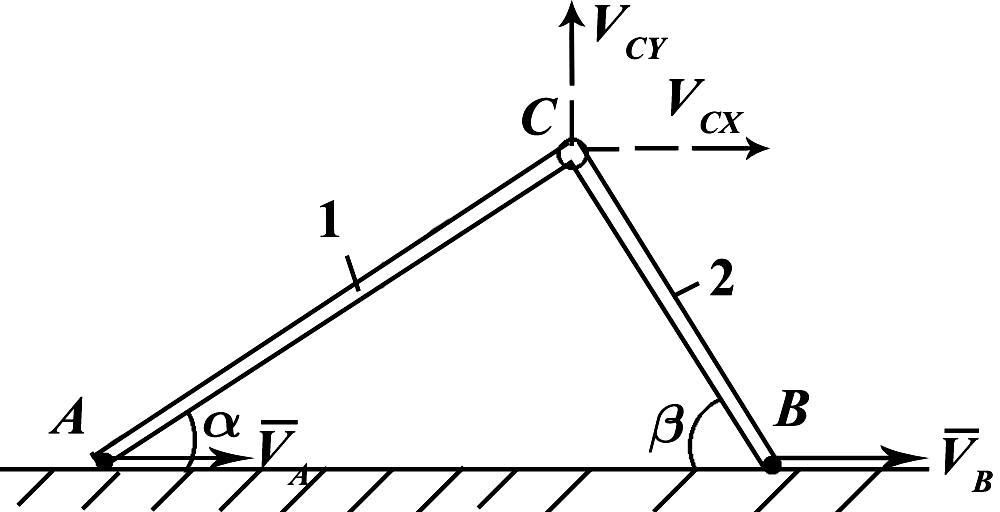
Рис.
П.34
Предположив,
что
,
можем записать:
1) для
тела 1:
,
или
(1)
2) для
тела 2 аналогично:
(2)
В
заданном конкретном положении механизма
выражения (1) и (2) приобретают вид
(рис.П.34):

или
(3)
Решая
полученную систему (3), находим:
;
;
.
Истинную
картину движения механизма покажем на
рис.
П.35.
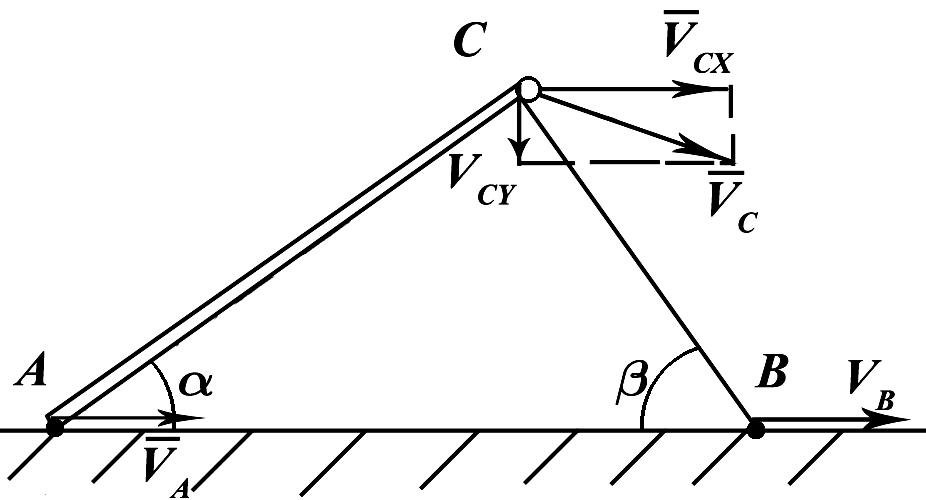
Рис.
П.35
ЛИТЕРАТУРА
-
А.
А., Яблонский, В. М., Никифорова. Курс
теоретической механики. –
Ч. 1. – М.: Высш. шк., 1984 и последующие
издания. -
М.
И., Бать, Г. Ю., Джанелидзе, А. С., Кельзон.
Теоретическая механика в примерах и
задачах. – Ч. 1. – М.: Высш. шк., 1984. -
Н.
Н., Никитин и др. Курс теоретической
механики. – М.: Высш. шк., 1983. -
С.
М., Тарг. Краткий курс теоретической
механики. – М.: Высш. шк.,
1986 г. и последующие издания. -
Сборник
заданий для курсовых работ по теоретической
механике /
под. общ. ред. А. А. Яблонского. – М.: Высш.
шк., 1985.
Учебное издание
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
v2 < v1
то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:


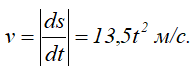
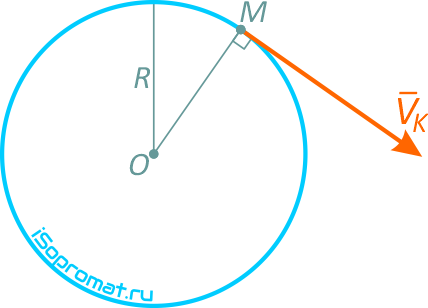
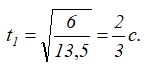
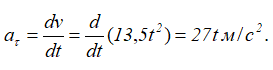
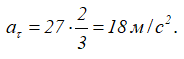
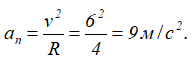
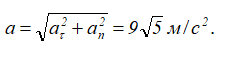
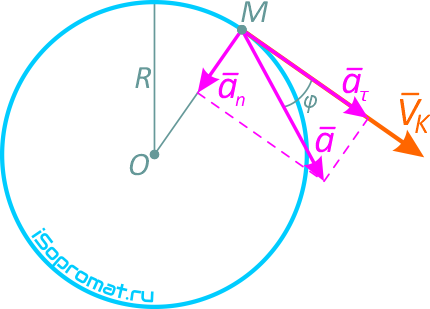
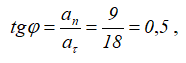
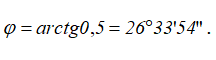



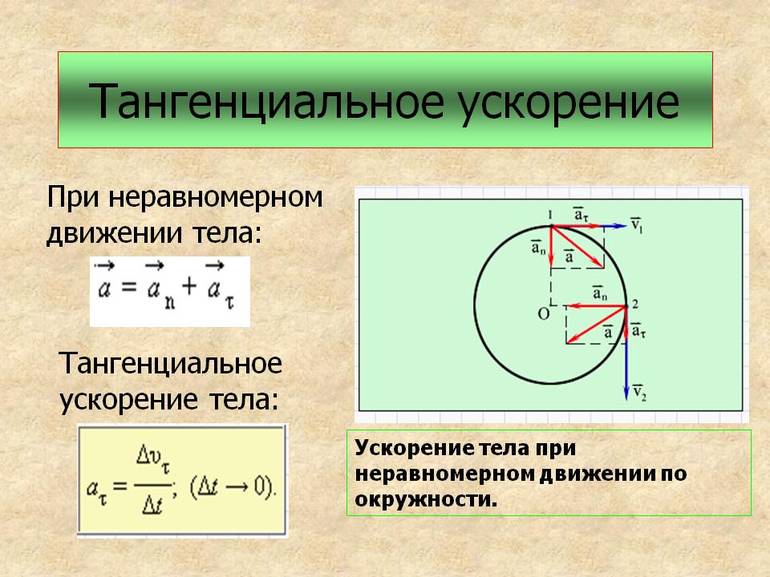
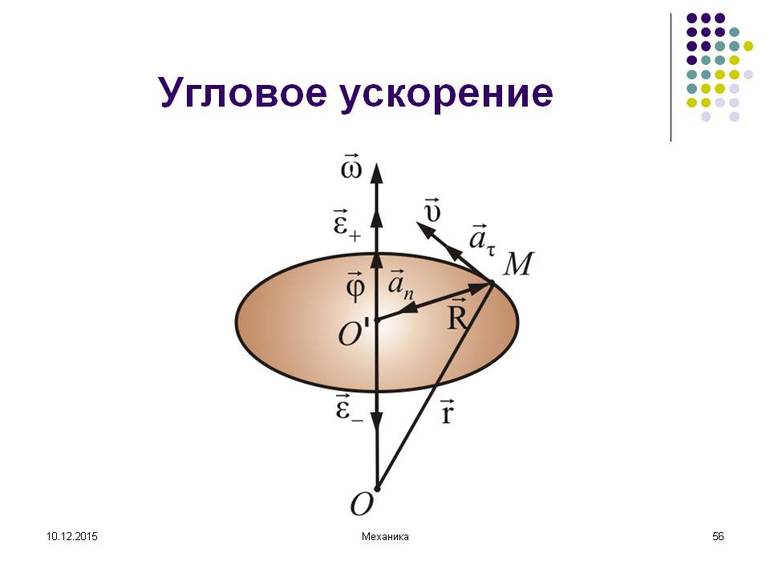
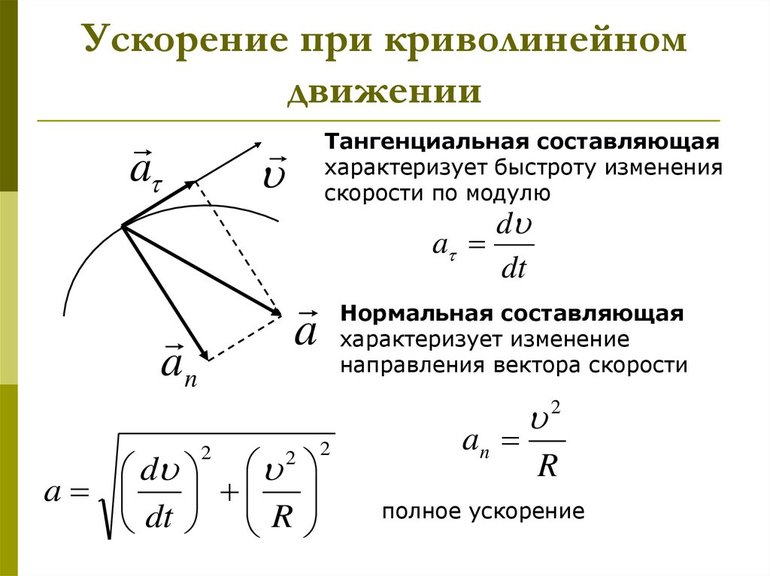









.</p>
<p style=)




















.</li>
<li>Интернет-портал Gym1belovo.smartlearn.ru (Источник).</li>
<li>Интернет-портал Studopedia.info (Источник).</li>
</ol>
<p style=) Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.