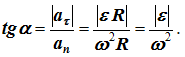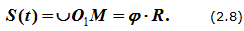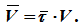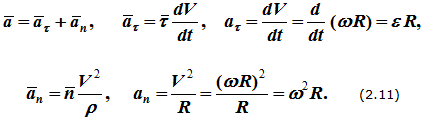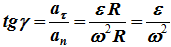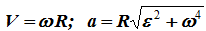Так
как траектории точек вращающегося тела
– окружности, при определении скорости
и ускорения удобно воспользоваться
естественным способом задания движения
(рисунок 1.5). Дуговая координата,
определяющая положение точки на
траектории, связана с углом поворота
равенством:
s
= φR .
Отсюда:
Рис.
1.5
Скорость ν
= νττ еще
называют линейной или окружной
скоростью.
Она направлена по касательной к траектории
движения точки.
Ускорение
(рисунок 1.6) определяется как сумма
касательного и нормального ускорений:
модуль
ускорения
Рис.
1.6
Угол α,
образованный вектором ускорения точки
с радиусом окружности OM,
для всех точек тела в любой момент
времени одинаков,
Касательное
и нормальное ускорения при вращательном
движении твердого тела также называют
соответственно вращательным и
центростремительным:
Векторные
выражения скорости и ускорения точек
вращающегося тела
Модуль
скорости точки вращающегося тела ν
= ωR = ωr sinβ
(рисунок 1.7) равен модулю векторного
произведения ω⊗r.
Рис.
1.7
Следовательно:
ν
= ω×r
(формула
Эйлера).
Определим
ускорение точки, продифференцировав
формулу Эйлера:
Первое
слагаемое является касательным
ускорением aτ= ε ⊗ r,
а
второе – нормальным an = ω ⊗ (ω ⊗ r) = ω ⊗ ν.
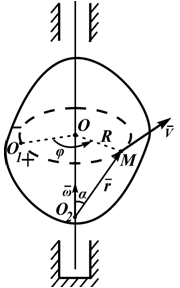
Рассмотрим определение скоростей и ускорений точек вращающегося твердого тела:
Рисунок 2.4
При вращении твердого тела вокруг неподвижной оси каждая точка тела движется по окружности. Радиус окружности R равен расстоянию от точки до оси вращения.
Закон движения точки может быть задан естественным способом (рисунок 2.4): траектория – окружность; начало отсчета точка O1 и положительное направление движения выбраны, длина дуги (дуговая координата) определяется по формуле
Скорости точек
Скорость точки вращающегося твердого тела определяется выражением
V=dS/dt=dφ∙R/dt=ωR (2.9)
где ω — угловая скорость вращения твердого тела.
Скорость направлена по касательной к траектории, поэтому можно написать
Вектор скорости можно получить векторным произведением:
V=ω × r,
V=ω × r × sinα=ω×R.
Ускорения точек
Ускорение точки при естественном способе задания движения определяется как сумма касательного и нормального ускорений (см. вывод формулы (1.10)):
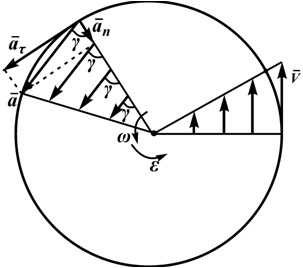
Рисунок 2.5
Эти же выражения можно получить, взяв производную от векторного произведения V=ω × r.
Угол, который составляет полное ускорение с радиусом, может быть определен из соотношения (рисунок 2.5)
То есть эти углы для всех точек тела одинаковы и не зависят от их расположения на теле. На этом же рисунке представлены законы распределения скоростей и ускорений точек во вращающемся теле в зависимости от расстояния их до оси вращения. Эти законы распределения соответствуют формулам:
>> Передаточные механизмы
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
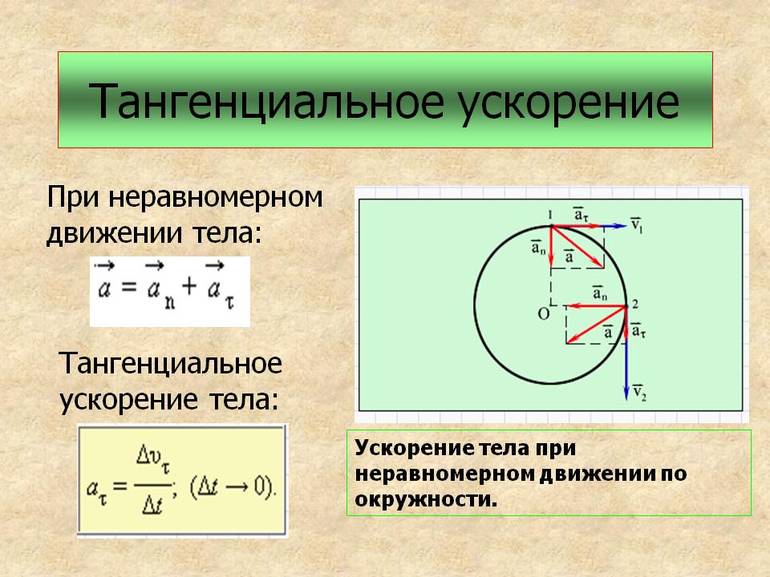
Тангенциальное ускорение
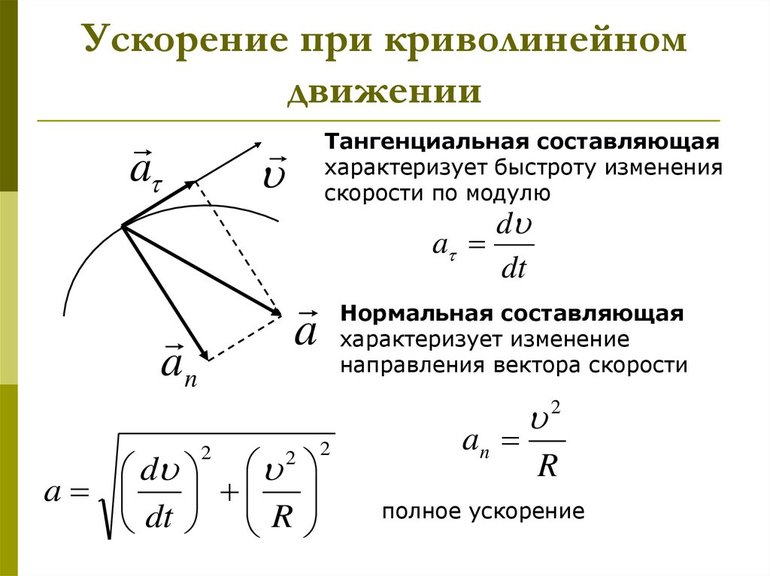
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Тангенциальное ускорение — определение, формула и измерение
Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
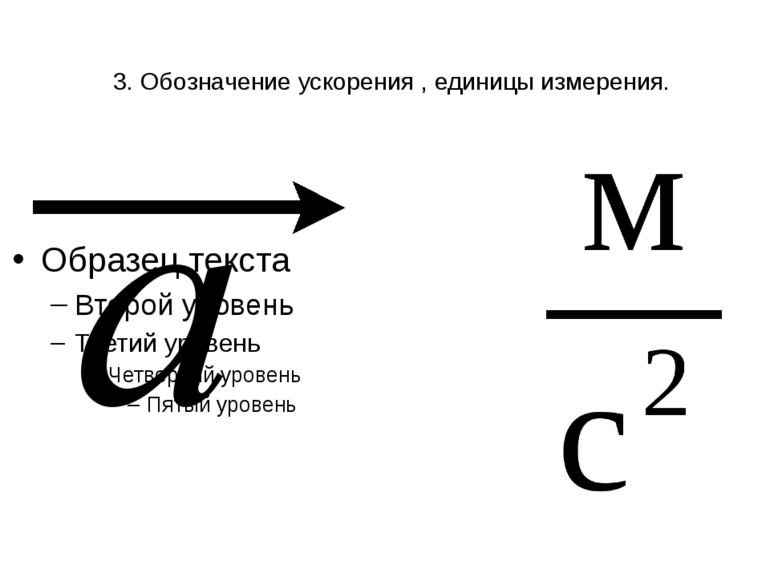
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
- Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
- Нормальное — совпадающее с нормалью траектории изменения положения.
- Полное — определяющееся суммой тангенциального и нормального ускорений.
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
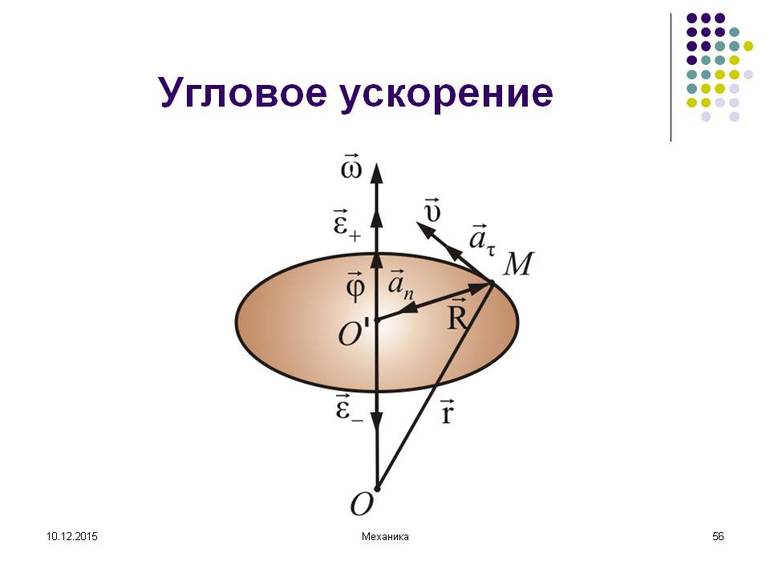
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
- Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
- Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
- at — тангенциальной составляющей, совпадающей с отрезком V;
- an — перпендикулярным по отношению расположения V вектором.
Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2 .
Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
- Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t 3 . Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения. Подставив заданные значения, можно получить: w = d φ / dt = -1 + 0,2 * 3t 2 и e = dw / dt = 0,6 * 2t. Применив формулу связи, легко найти ускорение: at = R * E * (0,6 * 2t) = 1,2 * Rt = 24 м 2 /с. Подставив в формулу нормального ускорения значения, можно вычислить и его an = V 2 / R = R * (0,6 * 10 2 — 1) 2 / 0,2 = 696 м/с 2 . Отсюда полное ускорение будет равняться: a = √ 24 2 + 696 2 = 697 м/с 2 .
- Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at. При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Нормальное ускорение можно выразить через скорость и радиус: an = V 2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V 2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V 2 / R = — dV / dt.
Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V 2 . В итоге должно получиться выражение: dV / V 2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
Движение материальной точки по окружности. Центростремительное ускорение.
Линейная и угловая скорости
Движение по окружности нас окружает постоянно – это может быть мотоциклист на мототреке, вращение грузика на веревке, движение по выгнутому круглому мосту, любой поворот на дороге тоже можно рассматривать, как движение по части окружности и т.д.
Давайте представим, что мы смотрим сверху на мототрек (см. рис.1.). Пусть точка (А) это мотоциклист, который движется с постоянной линейной скоростью (vec), и за какое-то время (t) он переместится по дуге окружности (^<’>) в точку (^<’>). Его пройденный путь будет равен длине дуги окружности (^<’>).
Определение Линейная скорость – это путь, который проходит мотоциклист за единицу времени (например, за секунду):
Понятно, что чем больший путь (большую длину дуги) успевает пройти тело за одно и тоже время, тем быстрее оно движется, тем больше его линейная скорость. Линейная скорость — это обычная скорость, к которой мы все привыкли. Обратите внимание, что вектор линейной скорости всегда направлен по касательной к траектории, в нашем случае – по касательной к окружности. Чуть позже нам это пригодится.
И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.
Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок (^<’>O) — точка (A) переходит в точку (^<’>), а точка (B) – в точку (^<’>).
При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности (^<’>), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние (^<’>).
А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?
Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.
И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:
где (V) – линейная скорость,
(omega) – угловая скорость,
(R) – радиус вращения.
Период и частота вращения
Важными характеристиками любого вращательного движения являются частота и период:
Определение Период – время, за которое тело совершает полный оборот.
В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.
Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac<2*pi*R>;$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac<2*pi><omega>;$$ Где (V) –линейная скорость вращения.
В системе СИ период измеряется в ([^<-1>]).
Определение Частота – количество оборотов за единицу времени.
В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.
Период и частота вращения связаны между собой выражением: $$T=frac<1><nu>;$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac<2*pi*R>=frac<omega><2*pi>;$$
Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.
Решение: Точка (А) находится дальше от центра на (20 (см)), а значит ее скорость больше, чем у точки (В). По условию так и есть. Так как обе точки находятся на одном радиусе, то угловые скорости у них одинаковые. Распишем угловые скорости для точек (А) и (В) и приравняем: $$omega_A=frac;$$ $$omega_B=frac;$$ $$omega_A=omega_B;$$ $$frac=frac;$$ Из условия (A0=BO+0.2): $$frac=frac;$$ $$frac<15>=frac<10>;$$ $$15*BO=(BO+0,2)*10;$$ $$5*BO=2;$$ $$BO=0,4.$$ Мы нашли радиус окружности по которой вращается точка (В), тогда радиус точки (А) будет на (0,2(м)) больше — (0,6(м)).
Для того, чтобы найти частоту, воспользуемся формулой: $$nu=frac<2*pi*R_A>=frac<15><2*3,14*0,6>=3,98(об/сек);$$ Ответ: (R=0,6(м)) и (nu=3,98(об/сек).)
Центростремительное (нормальное) ускорение
Вернемся к нашему примеру с мотоциклистом, двигающимся по мототреку в форму окружности. (См. Рис.3.) Для начала, представим, что линейная скорость у мотоциклиста постоянна, то есть он двигается равномерно, а значит его ускорение должно быть равно нулю. Это действительно так, но при движении по окружности (или любой другой криволинейной траектории) даже с постоянной скоростью возникает новый вид ускорения – центростремительное, еще его называют «нормальное», ускорение. Оно появляется по причине изменения направления вектором скорости.
На самом деле, для решения задач понимать природу центростремительного ускорения совсем необязательно. Достаточно просто помнить, что при любом криволинейном движении появляется такое ускорение. Его можно вычислить по формуле: $$a_n=frac;$$ где (V) –линейная скорость;
(R) – радиус окружности.
Подставим сюда линейную скорость через угловую — (V=omega*R). И получим еще одну формулу для центростремительного ускорения: $$a_n=omega^2*R;$$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.
Тангенциальное ускорение
Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.
Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.
Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec>))
При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле: $$a_<tau>=frac;$$ где (V_к) – конечная скорость;
(V_н) – начальная скорость;
(t) – время, за которое скорость изменилась с (V_н) до (V_к).
При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.
Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).
Если тело движется по прямой, то нормальное ускорение равно (0).
Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec)).
Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса
Решение: Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость: $$a_n=omega^2*r;$$ Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3). $$a_=omega^2*frac<2>;$$ $$a_=omega^2*frac<3>;$$ $$frac>>=frac<omega^2*frac<2>><omega^2*frac<3>>=frac<2>*frac<3>=1,5$$ Ответ:(frac>>=1.5.)
http://nauka.club/fizika/tangentsialno%D0%B5-uskoreni%D0%B5.html
http://sigma-center.ru/circularmotion