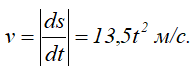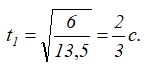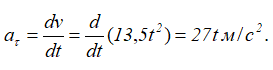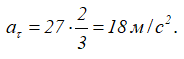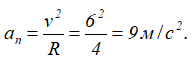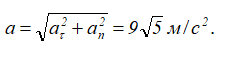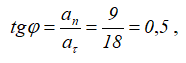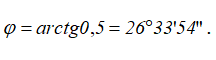Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Нормальное ускорение точки на окружности
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Движение по окружности
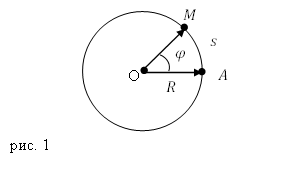
Значимым частным случаем перемещения материальной точки по заданной траектории служит движение по окружности. Местоположение точки на окружности можно задавать не при помощи расстояния от некоторой начальной точки (допустим A), а с помощью угла $varphi $, который образуют радиусы, которые провели из центра окружности (O) к рассматриваемой частице (точка M) и из О в точку начала отсчета (A) (рис.1).
Скорость при движении по окружности
При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла $varphi $:
Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:
тогда изменение длины дуги за время$ Delta t$ равно$ Delta s$:
[Delta s=RDelta varphi left(3right).]
Найдем отношение $frac $, разделив обе части выражения (3) на $Delta t$:
Перейдем к пределу в правой и левой частях равенства (4) при $Delta tto 0$, получим:
Ускорение материальной точки при движении по окружности
Величина нормальной (центростремительной) компоненты ускорения вычисляется при помощи формулы:
При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const). $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:
Период и частота — характеристики равномерного движения по окружности
Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($nu$) обращения, которую определяют как величину обратную периоду, равную количеству оборотов за единицу времени:
При равномерном движении по окружности угловая скорость, частота и период связаны как:
Формула (9) дает возможность центростремительное ускорение определить как:
Отметим, что при неравномерном движении по окружности период ($T$) и частота ($nu$) свой смысл теряют, о них можно говорить только при равномерном движении по окружности.
Примеры задач с решением
Задание. Центростремительное ускорение материальной точки, перемещающейся по окружности, имеющей радиус R, задано уравнением: $a_n=A+Bt+Ct^2(frac )$. Каково тангенциальное ускорение точки? Как направлены ускорения точки?
Решение. Сделаем рисунок.
Нормальное ускорение материальной точки, движущейся по окружности можно найти как:
Следовательно, скорость точки:
Используя заданный в условии задачи закон изменения нормального ускорения $a_n=A+Bt+Ct^2(frac )$, выражение (1.3) преобразуем к виду:
Величина тангенциального ускорения определена как:
Подставим правую часть выражения (1.4) в уравнение (1.5), имеем:
Задание. Чему равен путь (s), который проходит точка в примере 1 за время $t_1$, если A= 1 $frac $, $B=6 frac $; $С=9frac $.
Решение. Путь, пройденный точкой можно найти как:
Используем выражение для величины скорости, которое мы получили в первом примере:
Подставим известные нам из условия задачи коэффициенты, преобразуем полученное выражение $v left(tright):$
Вычислим интеграл (2.1), принимая во внимание выражение (2.3):
Ответ. $s=sqrt left(t_1+frac ^2right)$
Движение материальной точки по окружности. Центростремительное ускорение.
Линейная и угловая скорости
Движение по окружности нас окружает постоянно – это может быть мотоциклист на мототреке, вращение грузика на веревке, движение по выгнутому круглому мосту, любой поворот на дороге тоже можно рассматривать, как движение по части окружности и т.д.
Давайте представим, что мы смотрим сверху на мототрек (см. рис.1.). Пусть точка (А) это мотоциклист, который движется с постоянной линейной скоростью (vec ), и за какое-то время (t) он переместится по дуге окружности (^ ) в точку (^ ). Его пройденный путь будет равен длине дуги окружности (^ ).
Определение Линейная скорость – это путь, который проходит мотоциклист за единицу времени (например, за секунду):
Понятно, что чем больший путь (большую длину дуги) успевает пройти тело за одно и тоже время, тем быстрее оно движется, тем больше его линейная скорость. Линейная скорость — это обычная скорость, к которой мы все привыкли. Обратите внимание, что вектор линейной скорости всегда направлен по касательной к траектории, в нашем случае – по касательной к окружности. Чуть позже нам это пригодится.
И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.
Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок (^ O) — точка (A) переходит в точку (^ ), а точка (B) – в точку ( ^ ).
А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?
Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.
И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:
где (V) – линейная скорость,
(omega) – угловая скорость,
(R) – радиус вращения.
Период и частота вращения
Важными характеристиками любого вращательного движения являются частота и период:
Определение Период – время, за которое тело совершает полный оборот.
В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.
Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac ;$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac ;$$ Где (V) –линейная скорость вращения.
В системе СИ период измеряется в ([ ^ ]).
Определение Частота – количество оборотов за единицу времени.
В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.
Период и частота вращения связаны между собой выражением: $$T=frac ;$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac =frac ;$$
Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.
Для того, чтобы найти частоту, воспользуемся формулой: $$nu=frac =frac =3,98(об/сек);$$ Ответ: (R=0,6(м)) и (nu=3,98(об/сек).)
Центростремительное (нормальное) ускорение
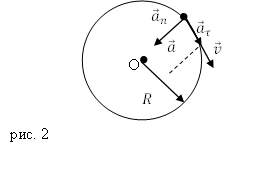
Вернемся к нашему примеру с мотоциклистом, двигающимся по мототреку в форму окружности. (См. Рис.3.) Для начала, представим, что линейная скорость у мотоциклиста постоянна, то есть он двигается равномерно, а значит его ускорение должно быть равно нулю. Это действительно так, но при движении по окружности (или любой другой криволинейной траектории) даже с постоянной скоростью возникает новый вид ускорения – центростремительное, еще его называют «нормальное», ускорение. Оно появляется по причине изменения направления вектором скорости.
На самом деле, для решения задач понимать природу центростремительного ускорения совсем необязательно. Достаточно просто помнить, что при любом криволинейном движении появляется такое ускорение. Его можно вычислить по формуле: $$a_n=frac ;$$ где (V) –линейная скорость;
(R) – радиус окружности.
Подставим сюда линейную скорость через угловую — (V=omega*R). И получим еще одну формулу для центростремительного ускорения: $$a_n=omega^2*R;$$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.
Тангенциальное ускорение
Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.
Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.
Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec>))
При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле: $$a_ =frac ;$$ где (V_к) – конечная скорость;
(V_н) – начальная скорость;
(t) – время, за которое скорость изменилась с (V_н) до (V_к).
При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.
Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).
Если тело движется по прямой, то нормальное ускорение равно (0).
Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec)).
Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса
Решение: Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость: $$a_n=omega^2*r;$$ Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3). $$a_ =omega^2*frac ;$$ $$a_ =omega^2*frac ;$$ $$frac>>=frac > >=frac *frac =1,5$$ Ответ:(frac>>=1.5.)
iSopromat.ru
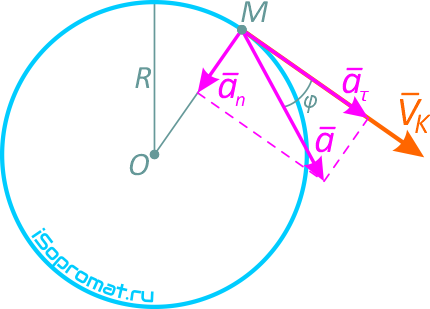
Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Задача
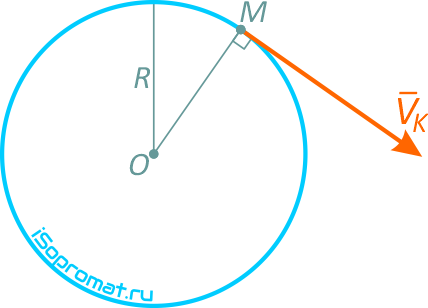
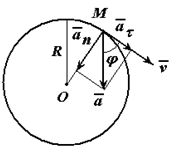
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
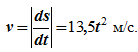
Подставляя в это выражение значение скорости, получим 6=13,5t1 2 , откуда находим
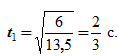
Касательное ускорение для любого момента времени равно
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
Модуль вектора полного ускорения точки равен
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
http://b4.cooksy.ru/articles/normalnoe-uskorenie-tochki-na-okruzhnosti
При произвольном
криволинейном движении вектор скорости
может изменяться как по величине, так
и по направлению. В этом случае существует
ускорение, характеризующее быстроту
изменения скорости по величине, и
ускорение, характеризующее быстроту
изменения скорости по направлению.
Рассмотрим три
частных случая.
При движении по
прямолинейной траектории
—
орт скоростиостается постоянным, т.е.
=сonst,
поэтому
.
Если0,
то ускорение направлено так же, как и
скорость. Если
0,
направление ускорения противоположно
направлению скорости. Модуль ускорения
равен
.
При равномерном
движении по окружности =сonst,
изменяется
(рис.1.6,а),
поэтому:
.
(1.4)
Найдем производную
орта скорости
.
s
R
О
а)
б)
Рис.1.6
Из рис.1.6 видно,
что за время t
орт скорости поворачивается на угол
и получает приращение
.
По определению
.
При
и
.
Тогда,
— еди-ничный вектор, имеющий такое же
направление, как и.
При произвольном
переходе единичный вектор
превращается в
-орт
нормали к траектории в той точке, в
которой частица была в моментt.
Таким образом,
.
(1.5)
Подставив (1.5) в
(1.4), получим
— нормальное уско-рение.
При равномерном
движении по окружности ускорение
направлено по нормали к скорости. Поэтому
называют его нормальным ускорением и
в обозначении ставят индекс n.
При неравномерном
движении частицы по криволинейной
траектории оба множителя в формуле
изменяются со временем. Применив правило
дифференцирования произведения функций,
найдем выражение для ускорения
.
Видно, что в общем
случае ускорение распадается на два
слагаемых. Одно из них
коллинеарно скорости и, следовательно,
направлено по касательной к траектории.
Поэтому его называют тангенциальным
(т.е. касательным) ускорением и обозначают.
Второе слагаемое
совпадает с
,
т.е. определяется формулойи является нормальным ускорением. Первое
слагаемое характеризует быстроту
изменения модуля скорости, второе
быстроту изменения направления скорости.
Составляющиеи
перпендикулярны друг другу (рис.1.7).
Поэтому квадрат модуля ускорения равен
сумме квадратов модулей составляющих.
|
Рис.1.7 |
Отсюда
|
1.4. Движение точки по окружности. Угловая скорость. Угловое ускорение
При вращении
твердого тела все его точки движутся
по окружности, центры которых лежат на
единой прямой, называемой осью вращения.
Окружности, по которым движутся точки
тела, лежат в плоскости, перпендикулярной
к этой оси.
Радиус-вектор
каждой точки – есть вектор, проведенный
из центра окружности в данную точку. Он
поворачивается за время t
на один и тот же угол .
Векторная величина
называется угловой скоростью, гдеt
– время, за
которое совершается поворот на угол
.
Из определения видно, что вращение точки
по окружности описывается угловой
скоростью
.
|
Вектор |
М1 Рис.1.8 |
ра угловой скорости.
При равномерном
вращении угловая скорость
,
а угол поворота.
Единицей угловой
скорости в системе СИ является радиан
в секунду
.
Угловая скорость
— есть величина постоянная, она указывает,
на какой угол поворачивается тело за
единицу времени. В этом случае она
называется круговой или циклической
частотой.
Равномерное
движение можно охарактеризовать также
периодом обращения. Периодом называется
время, за которое тело делает один
оборот, т.е. поворачивается на угол 2.
Поскольку за время, равное Т совершается
угол поворота 2,
то
;
.
Число оборотов за
единицу времени (частоту) обозначим
и выразим период и циклическую частоту
через эту величину
;
;
.
Угол поворота за
время t
можно записать через частоту
и полное
число оборотов
N
;
.
При неравномерном
вращении величина
изменяется со временем и за промежуток
времени t
получает приращение .
Величина,
характеризующая изменение вектора
угловой скорости со временем, называется
угловым ускорением
.
Таким образом,
изменение угловой скорости по времени
характеризуется угловым ускорением
,
которое определяется как производная
угловой скорости по времени
.
Единица измерения
углового ускорения
.
При неподвижной оси вращения векторыи
коллинеарны и направлены вдоль оси
вращения. Если угловая скорость
увеличивается,
то векторыи
одинаково направлены, если угловая
скорость уменьшается,
то векторыи
противоположно направлены.
При неравномерном
вращении для угла поворота, угловой
скорости и ускорения справедливо
соотношение
,
где
0
– начальная угловая скорость.
Найдем соотношение
между
(рис.1.9).
|
М1 R s М2 Рис.1.9 |
Пусть за малый
Величина |
Подставляя значение
s
из предыдущего равенства, получим
,
т.е. линейная
скорость точки прямо пропорциональна
радиусу и угловой скорости
.
(1.6)
Выясним соотношение
между
и
.
Нормальное ускорение точек прямо
пропорционально квадрату линейной
скорости и обратно пропорционально
радиусу
.
(1.7)
Подставляя в
уравнение (1.7) уравнение (1.6), получим
следующее выражение для нормального
ускорения:
.
Модуль тангенциального
ускорения равен модулю первой производной
от линейной скорости
.
(1.8)
Подставляя (1.6) в
уравнение (1.8) найдем, что
.
Но так как
,
то.
Для нахождения соотношения между
векторамии
сделаем чертеж (рис.1.10). Пусть тело
вращается вокруг осиz
с угловой скоростью
.
Выберем точку О на оси и проведем
радиус-векториз этой точки к точке С. Из треугольника
ОАС видно, что.
Умножим обе части равенства на
и получим cледующее выражение:
.
Так как
— модуль скорости,
— модуль векторного произведения
,
то
.
Откуда следует,
что вектор скорости равен векторному
произведению вектора угловой скорости
на радиус-вектор
:
.
(1.9)
Формуле (1.9) можно
придать иной вид. Для этого представим
|
A C
O Рис.1.10 |
радиус-вектор
Векторы |
.
(1.10)
Выведем соотношение
для тангенциального и углового ускорения.
По определению тангенциальное ускорение
есть первая производная от вектора
скорости по времени (1.8). Подставляя
(1.10) в (1.8), получим
,
т. е.
.
Иногда удобно рассмотреть скорость движения тела по окружности через угловую скорость. Она показывает, на какой угол успевает повернуться тело за единицу времени. На Рис.1. мотоциклист, переместившись из точки (A) в точку ({A}^{’}), повернулся на угол (Delta varphi) за время (t).
$$omega=frac{Deltavarphi}{t} , (рад/сек);$$
В международной системе единиц измерения угловую скорость принято измерять в радианах в секунду. Кроме обычных градусов углы можно измерять в радианах, с ними вы должны были столкнуться в школьном курсе тригонометрии.
И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.
Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок ({A}^{’}O) — точка (A) переходит в точку ({A}^{’}), а точка (B) – в точку ({B}^{’}).
При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности ({AA}^{’}), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние ({BB}^{’}).
Выпишем формулы для линейных скоростей точек (A) и (B):
$$V_{A}=frac{{AA}^{’}}{t};$$
$$V_{B}=frac{{BB}^{’}}{t};$$
Из рисунка 1 видно, что ({AA}^{‘}>{BB}^{‘}), а значит линейная скорость точки (A) больше скорости точки (B):
$$V_{A}>V_{B};$$
Можно сделать важный вывод, что чем дальше точка находится от центра, тем больше ее скорость относительно точек, находящихся на этой же прямой.
А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?
Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.
И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:
$$V=omega*R; ,,(1)$$
где (V) – линейная скорость,
(omega) – угловая скорость,
(R) – радиус вращения.
Тангенциальное ускорение
Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.
Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.
Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec{a_{/tau}}))
При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле:
$$a_{tau}=frac{V_к-V_н}{t};$$
где (V_к) – конечная скорость;
(V_н) – начальная скорость;
(t) – время, за которое скорость изменилась с (V_н) до (V_к).
При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.
Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).
Если тело движется по прямой, то нормальное ускорение равно (0).
Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec{a})).
Пример 2
Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса
Решение:
Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость:
$$a_n=omega^2*r;$$
Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3).
$$a_{nA}=omega^2*frac{R}{2};$$
$$a_{nB}=omega^2*frac{R}{3};$$
$$frac{a_{nA}}{a_{nB}}=frac{omega^2*frac{R}{2}}{omega^2*frac{R}{3}}=frac{R}{2}*frac{3}{R}=1,5$$
Ответ:(frac{a_{nA}}{a_{nB}}=1.5.)
Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Задача
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t3 (s в метрах, t в секундах).
Рисунок 1.6
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
Другие примеры решений >
Помощь с решением задач >
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
Другие видео
Скорость точки направлена по касательной к траектории (окружности), т.е. перпендикулярно линии радиуса.
Подставляя в предыдущее выражение значение скорости, получим 6=13,5t12, откуда находим
Касательное ускорение для любого момента времени равно
При t=t1=2/3 с
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
Модуль вектора полного ускорения точки равен
Направление нормального, касательного и полного ускорений точки
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
отсюда
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее









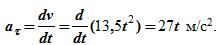
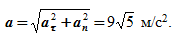




 z
z