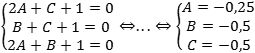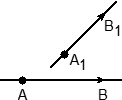Как найти нормальный вектор плоскости в пространстве

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

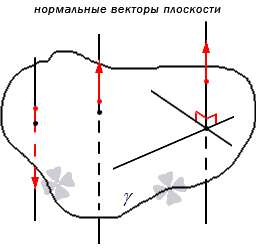
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Нормальный вектор плоскости, координаты нормального вектора плоскости.

Хорошее представление о прямой линии начинается с момента, когда вместе с ее образом одновременно возникают образы ее направляющих и нормальных векторов. Аналогично, при упоминании о плоскости в пространстве, она должна представляться вместе со своим нормальным вектором. Почему так? Да потому что во многих случаях удобнее использовать нормальный вектор плоскости, чем саму плоскость.

В этой статье мы сначала дадим определение нормального вектора плоскости, приведем примеры нормальных векторов и необходимые графические иллюстрации. Далее поместим плоскость в прямоугольную систему координат в трехмерном пространстве и научимся определять координаты нормального вектора плоскости по ее уравнению.

Навигация по странице.

Нормальный вектор плоскости – определение, примеры, иллюстрации.

Для хорошего усвоения материала нам потребуется хорошее представление о прямой в пространстве, представление о плоскости и определения из статьи векторы – основные определения.

Дадим определение нормального вектора плоскости.

Нормальный вектор плоскости — это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.

Из определения следует, что существует бесконечное множество нормальных векторов данной плоскости.

Так как все нормальные векторы заданной плоскости лежат на параллельных прямых, то все нормальные векторы плоскости коллинеарны. Другими словами, если — нормальный вектор плоскости , то вектор при некотором ненулевом действительном значении t также является нормальным вектором плоскости (смотрите статью условие коллинеарности векторов).

Также следует заметить, что любой нормальный вектор плоскости можно рассматривать как направляющий вектор прямой, перпендикулярной к этой плоскости.

Множества нормальных векторов параллельных плоскостей совпадают, так как прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и ко второй плоскости.

Из определения перпендикулярных плоскостей и определения нормального вектора плоскости следует, что нормальные векторы перпендикулярных плоскостей перпендикулярны.

Приведем пример нормального вектора плоскости.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz . Координатные векторы являются нормальными векторами плоскостей Oyz , Oxz и Oxy соответственно. Это действительно так, потому что векторы ненулевые и лежат на координатных прямых Ox , Oy и Oz соответственно, которые перпендикулярны координатным плоскостям Oyz , Oxz и Oxy соответственно.

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.

Озвучим цель, которая преследовалась при создании этого пункта статьи: научиться находить координаты нормального вектора плоскости, если известно уравнение плоскости в прямоугольной системе координат Oxyz .

Общее уравнение плоскости вида определяет в прямоугольной системе координат Oxyz плоскость, нормальным вектором которой является вектор . Таким образом, чтобы найти координаты нормального вектора плоскости нам достаточно иметь перед глазами общее уравнение этой плоскости.

Рассмотрим несколько примеров.

Найдите координаты какого-либо нормального вектора плоскости .

Нам дано общее уравнение плоскости, коэффициенты перед переменными x , y и z представляют собой соответствующие координаты нормального вектора этой плоскости. Следовательно, — один из нормальных векторов заданной плоскости. Множество всех нормальных векторов этой плоскости можно задать как , где t — произвольное действительное число, отличное от нуля.

Плоскость задана уравнением . Определите координаты ее направляющих векторов.

Нам дано неполное уравнение плоскости. Чтобы стали видны координаты ее направляющего вектора, перепишем уравнение в виде . Таким образом, нормальный вектор этой плоскости имеет координаты , а множество всех нормальных векторов запишется как .

Уравнение плоскости в отрезках вида , как и общее уравнение плоскости, позволяет сразу записать один из нормальных векторов этой плоскости – он имеет координаты .

В заключении скажем, что с помощью нормального вектора плоскости могут быть решены различные задачи. Самыми распространенными являются задачи на доказательство параллельности или перпендикулярности плоскостей, задачи на составление уравнения плоскости, а также задачи на нахождение угла между плоскостями и на нахождение угла между прямой и плоскостью.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

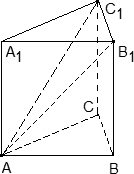
3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.



5.2.3. Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.

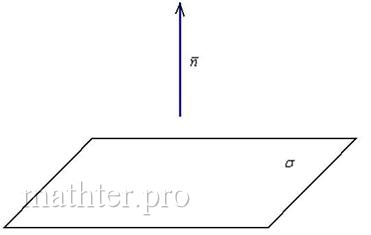
Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением  в прямоугольной (!) системе координат, то вектор  является нормальным вектором данной плоскости.

Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:

Задача 134

Найти единичный нормальный вектор плоскости .

Решение: принципиально ситуация выглядит так:

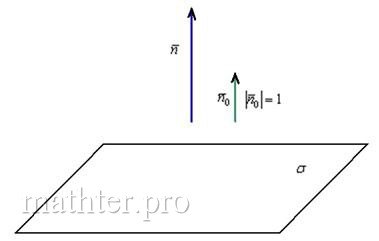
Сначала из уравнения плоскости «снимем» вектор нормали: .

И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора  разделить на длину вектора .

Вычислим длину вектора нормали:

Таким образом:

Контроль: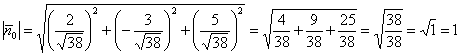, ОК

Ответ:

Вспоминаем, что координаты этого вектора  – есть в точности направляющие косинусы вектора : .

И, как говорится, обещанного три страницы ждут   – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке  и двум векторам , и в результате решения мы получили уравнение .

Проверяем:

Во-первых, подставим координаты точки  в полученное уравнение:

 – получено верное равенство, значит, точка  лежит в данной плоскости.

На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы  параллельны плоскости, а вектор  ей перпендикулярен, то должны иметь место следующие факты: . Ортогональность векторов элементарно проверяется с помощью скалярного произведения:

Вывод: уравнение плоскости найдено правильно.

В ходе проверки я фактически процитировал следующее утверждение теории: вектор  параллелен плоскости  в том и только том случае, когда .

Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:

5.2.4. Как составить уравнение плоскости по точке и вектору нормали?

5.2.2. Как составить уравнение плоскости по трём точкам?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Определение 1. Уравнение с
тремя переменнымиAx + By + Cz + D = 0,
гдеA, B и Cне равны 0 одновременно, называетсяобщим уравнением плоскости.

Основные виды уравнений плоскости в
трехмерном пространстве:

1) z = 0- уравнение плоскостиOxy;

2) y = 0- уравнение плоскостиOxz;

3) x = 0- уравнение плоскостиOyz;

4) Cz + D = 0- уравнение плоскости, параллельной
плоскостиOxy;

5) By + D = 0- уравнение плоскости, параллельной
плоскостиOxz;

6) Ax + D = 0- уравнение плоскости, параллельной
плоскостиOyz;

7) Ax + By + D = 0- уравнение плоскости, параллельной оси
координатOx;

 Ax + Cz + D = 0- уравнение плоскости, параллельной оси
координатOy;

9) Ax + By + D = 0- уравнение плоскости, параллельной оси
координатOz;

10) Ax + By + Cz = 0- уравнение плоскости, проходящей через
начало координат.

Теорема 1. Любая плоскость в
трехмерном пространстве может быть
задана общим уравнением.

Определение 2.Вектор(A, B, C)называетсяобщим нормальным вектором
плоскостиAx + By + Cz + D = 0.

Если две плоскости заданы общими
уравнениями A₁x + B₁y + C₁z + D₁ = 0
иA₂x + B₂y + C₂z + D₂ = 0,
то:

— плоскости параллельны тогда и только
тогда, когда их нормальные векторы
коллинеарны:
;

— плоскости перпендикулярны тогда и
только тогда, когда скалярное произведение
их нормальных векторов равно нулю:
A₁A₂ + B₁B₂ + C₁C₂ = 0.

A(x—x₀) + B(y—y₀) + C(z—z₀) = 0-уравнение прямой, проходящей через
точку(x₀, y₀, z₀),перпендикулярно нормальному вектору.

31. Уравнения прямой линии в
пространстве как линии пересечения
двух плоскостей. Канонические уравнения
прямой. Направляющий вектор прямой.
Условия параллельности и перпендикулярности
двух прямых в пространстве

Существует несколько способов задания
прямой в трехмерном пространстве:

1) — прямая как линия пересечения двух
плоскостей задается аналитически
системой двух линейных уравнений;

2) — канонические уравнения прямой, где(m, n, p) –
направляющий вектор прямой (т.е. прямая
параллельна этому вектору),M₁(x₁, y₁, z₁) –
некоторая точка, лежащая на данной
прямой.

Если две прямые заданы каноническими
уравнениями

и
,
то:

— прямые параллельны тогда и только
тогда, когда их направляющие векторы
коллинеарны:
;

— прямые перпендикулярны тогда и
только тогда, когда скалярное произведение
их направляющих векторов равно нулю:
m₁m₂ + n₁n₂ + p₁p₂ = 0;

42. Углы между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Условия параллельности и перпендикулярности двух плоскостей, двух прямых, прямой и плоскости

Если две плоскости заданы общими
уравнениями A₁x + B₁y + C₁z + D₁ = 0
иA₂x + B₂y + C₂z + D₂ = 0,
то уголмежду
плоскостями равен углу между нормальными
векторами(A₁, B₁, C₁)и(A₂, B₂, C₂),
следовательно,

.

Если две прямые заданы каноническими
уравнениями

и
,
то уголмежду
прямыми равен углу между направляющими
векторами(m₁, n₁, p₁)и(m₂, n₂, p₂),
следовательно,

.

Если плоскость задана общим уравнением
Ax + By + Cz + D = 0,
а прямая задана каноническими уравнениями
,
то уголмежду
прямой и плоскостью равен дополнительному
углу к углу между нормальным вектором(A, B, C)и направляющим вектором(m, n, p),
следовательно,

.

В последнем случае:

— плоскость и прямая параллельны
тогда и только тогда, когда скалярное
произведение их нормального и направляющего
векторов равно нулю:

Am + Bn + Cp = 0.

— плоскость и прямая перпендикулярны
тогда и только тогда, когда их нормальный
и направляющий векторы коллинеарны:

.

Соседние файлы в папке Линейная алгебра

• #
• #
• #
• #
• #
• #
• #

Нормальный вектор плоскости — наиболее компактный и наглядный способ определить плоскость в трехмерной системе координат.

Для каждой плоскости существует бесконечное множество коллинеарных друг по отношению к другу нормальных векторов.

В качестве примера плоскостей, задаваемых нормальными векторами, можно рассматривать координатные плоскости системы координат $Oxyz$: $Oxy$, $Oxz$, $Oyz$. Для них нормальными векторами будут, векторы, направляющие оси, т.е., соответственно, $Oz$, $Oy$ и $Ox$ ($vec{k}, vec{j}, vec{i}$).

Рассмотрим основные математические закономерности, показываюшие как найти вектор нормали к плоскости.

Формула нормального вектора выводится из общего уравнения плоскости, которое имеет вид $Ax + By + Cz + D = 0$.

Плоскости, в уравнениях которых один из коэффициентов равен $0$, соответствуют базовым плоскостям системы координат ($Oxy, Oxz, Oyz$).

Уравнения вида

$Ax + D = 0 \ By + D = 0 \ Cz + D = 0$

описывают плоскости, параллельные $Oxy, Oxz, Oyz$ и отстоящие от них на расстояние, равное отношению свободного члена $D$ к соответствующему коэффициенту, например:

$x = frac{D}{A}$

Нормальный вектор плоскости $Ax + By + Cz + D = 0$ можно выразить как $bar{n}(A; B; C)$. Существует бесконечное множество плоскостей, перпендикулярных данному вектору. Для определения плоскости нужна еще точка на ней. Через любую точку также можно провести бесконечное количество плоскостей (их совокупность называется связкой). Нормальный вектор и точка взаимодополняют друг друга, определяя единственную плоскость.

«Нормальный вектор плоскости» 👇

Точку на плоскости можно обозначить как $M_1(x; y; z)$. Вектор, соединяющий ее с любой другой точкой $M$ данной плоскости, при скалярном умножении на вектор нормали к плоскости $N$ дает ноль:

$overline{M_1M} cdot N = 0$

Переписав уравнение через проекции, получим

$overline{M_1M} cdot N = A(x — x_1) + B(y — y_1) + C(z — z_1) = 0$

Это дает нам возможность выводить уравнение плоскости через координаты точки и параметры нормального вектора плоскости.

С помощью нормального вектора плоскости как ее определителя могут быть решены задачи на доказательство параллельности или перпендикулярности плоскостей, на составление уравнения плоскости, на нахождение угла между прямой и плоскостью, на нахождение угла между плоскостями.

Метод координат в пространстве

30 мая 2011

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

1. Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

   

2. Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
3. Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую…

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Ответ: AB₁ = (1; 0; 1);

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

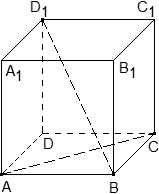
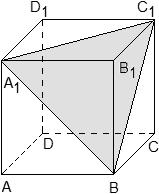
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

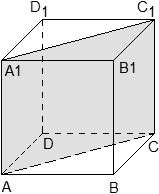
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

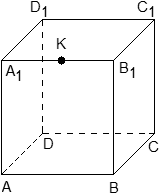
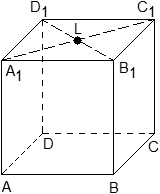
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Ответ: L = (0,5; 0,5; 1)

Смотрите также:

1. Введение системы координат
2. Четырехугольная пирамида в задаче C2
3. В 2012 году ЕГЭ по математике станет двухуровневым?
4. Сводный тест по задачам B12 (1 вариант)
5. Симметрия корней и оптимизация ответов в тригонометрии
6. ЕГЭ 2022, задание 6. Касательная и уравнение с параметром