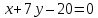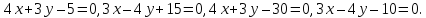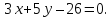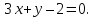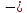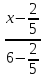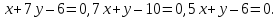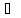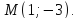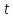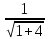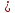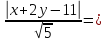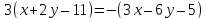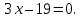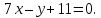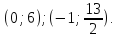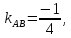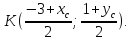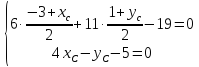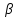Как найти вектор нормали зная направляющий вектор
Содержание
- Что такое направляющий вектор прямой
- Как вычислить координаты направляющего вектора по уравнениям прямой
- Направляющий вектор из канонического уравнения прямой и через две точки
- Направляющий вектор из параметрических уравнений
- Координаты направляющего вектора из общего уравнения
- Координаты направляющего вектора из уравнения с угловым коэффициентом
С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.
Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.
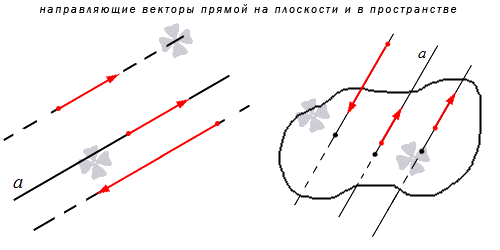
Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .
Как вычислить координаты направляющего вектора по уравнениям прямой
Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.
1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.
Решение
Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.
Ответ: 4 , — 3 .
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.
Решение
Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.
Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0
Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .
А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.
У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.
Решение
В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.
Ответ: ( 0 , 1 )
А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:
3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10
Получившееся равенство преобразовываем и получаем:
3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3
Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3
К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:
1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.
Решение
В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.
Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0
Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .
Решение
Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?
Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.
Решим задачу, в которой применяется этот подход.
Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .
Решение
Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .
У нас получится:
n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →
Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.
Ответ: — 20 , 10 , 0
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.
Направляющим вектором прямой называется вектор, параллельный прямой, которую он определяет или совпадающий с ней.
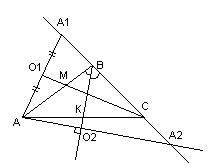
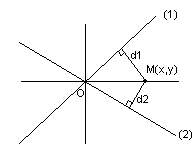
Рассмотрим прямую $L$, заданную точкой $M_0$, лежащей на ней, и направляющим вектором $overline$ с координатами $(l;m)$, при этом вектор $overline$ — ненулевой. Обозначим на прямой произвольную точку $M$ с координатами $(x, y)$, не совпадающую с точкой $M_0$. Радиус-векторы этих точек назовём $overline$ и $overline$. Вектор $overline$ при этом будет колинеарен вектору $overline$.
Вектор $overline$ можно выразить через сумму векторов $overline$:
$overline = overline + overlineleft(1
ight).$
Вектор $overline$ лежит на прямой $L$, поэтому он по условию является параллельным направляющему вектору $overline$ и связан с ним соотношением $overline= toverlineleft(2
ight)$, где $t$ — множитель, являющийся скалярной величиной и зависящий от позиции точки $M$ на прямой.
Рисунок 1. Направляющий вектор прямой L
Попробуй обратиться за помощью к преподавателям
Учитывая равенство $(2)$, формулу $(1)$ можно переписать следующим образом:
$overline = overline + toverlineleft(3
ight)$
Данное равенство носит название векторного уравнения прямой.
Возможны следующие варианты задания уравнения прямой на плоскости:
- Общее уравнение прямой;
- Уравнение с угловым коэффициентом;
- Через параметрические уравнения;
- Каноническое уравнение;
- С помощью двух точек, через которые проходит прямая.
Для каждого из этих вариантов подходит свой способ нахождения направляющего вектора.
Направляющий вектор из канонического уравнения прямой и через две точки
Каноническое уравнение прямой выглядит так:
Из канонического уравнения выразить координаты направляющего вектора проще всего: достаточно выписать знаменатели из уравнения следующим образом:
Уравнение прямой, проходящей через 2 точки, имеет вид, очень похожий на каноническое уравнение:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
$frac= fracleft(5
ight)$, где $(x_1; y_1)$ и $(x_2; y_2)$ — координаты точек, через которые проходит прямая.
В этом случае координаты направляющего вектора $overline$ равны $((x_2 – x_1); (y_2-y_1))$.
Даны две точки $(5; 10)$ и $(2;1)$. Составьте уравнение прямой и выпишите координаты направляющего вектора.
Подставим координаты данных точек в уравнение $(5)$ и получим:
Ответ: координаты направляющего вектора $overline$ равны $(3;9)$.
Направляющий вектор из параметрических уравнений
Параметрические уравнения имеют следующий вид: $egin x=x_0 + lt y=y_0 + mt end$
Для того чтобы выразить координаты направляющего вектора из параметрических уравнений, нужно выписать коэффициенты, стоящие перед параметром $t$, т.е. $overline=(l; m)$.
Координаты направляющего вектора из общего уравнения
Общее уравнение имеет следующий вид:
$Ax + By + C = 0left(6
ight)$
Для того чтобы получить координаты направляющего вектора, нужно от общего уравнения прямой перейти к каноническому.
Сделаем это в общей форме.
Сначала перенесём часть $By + C$ в правую часть:
Теперь разделим всё на $A$:
А после этого всё уравнение разделим на $B$:
Из вышеизложенного следует, что координаты направляющего вектора $overline$ будут равны $(B; -A)$.
Дано общее уравнение прямой $6x-7y + 5 = 0$. Получите направляющий вектор для данной прямой.
Воспользуемся уравнением прямой $(7)$. Из этого уравнения получается, что координаты направляющего вектора равны $(6;7)$.
Координаты направляющего вектора из уравнения с угловым коэффициентом
Уравнение с угловым коэффициентом имеет вид:
Для того чтобы получить из него координаты направляющего вектора, необходимо сначала привести его к общему виду, для этого переносим всё в левую часть:
Затем нужно воспользоваться алгоритмом для общего уравнения.
Уравнение с угловым коэффициентом, приведённое к каноническому, выглядит так:
то есть координаты направляющего вектора в данном случае будут $overline= (1;k)$.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Если даны две точки плоскости 

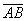
Если даны две точки пространства 

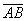
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание : Для тех же точек запишите формулы нахождения координат вектора 
Даны две точки плоскости 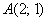
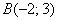
Решение: по соответствующей формуле:
Как вариант, можно было использовать следующую запись:
Эстеты решат и так:
Лично я привык к первой версии записи.
Ответ:
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 


Записи координат точек и координат векторов вроде бы схожи: 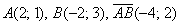
Дамы и господа, набиваем руку:
а) Даны точки 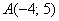

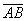

б) Даны точки 
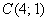
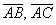
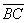
в) Даны точки 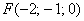

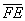
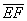
г) Даны точки 
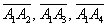
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Не нашли то, что искали? Воспользуйтесь поиском:
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением в декартовой системе координат, то вектор
является вектором нормали данной прямой.
Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали
достаточно просто «снять».
Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».


| Оглавление |
Автор: Aлeксaндр Eмeлин
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора 

Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
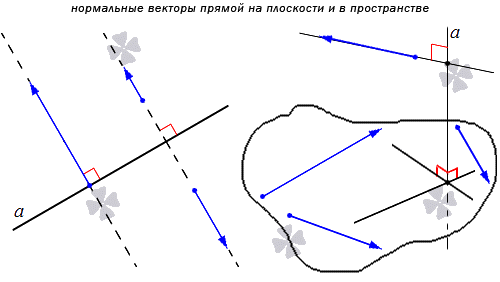
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y — 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .
Ответ: 3 , — 1 .
Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .
Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны — 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
Вектор нормали: расчет и пример
Содержание:
В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.
Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:
Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.
Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.
Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.
Как получить вектор нормали к плоскости?
Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.
Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:
К этой плоскости есть два нормальных вектора: п1 Y п2. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:
ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.
Ну, нормальный вектор к указанной плоскости задается следующим образом:
N = а я + b j + c k
Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.
Вектор нормали из векторного произведения
Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.
Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.
Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.
Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:
N = или Икс v
На следующем рисунке показана описанная процедура:
пример
Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).
Решение
Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.
Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:
AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k
Таким же образом поступаем и находим вектор AC:
AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k
Расчет векторного произведения AB x AC
Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:
Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:
я Икс я = 0; j Икс j = 0; k Икс k = 0
А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:
я Икс j = k ; j Икс k = я; k Икс я = j
Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):
j Икс я = – k; k Икс j = –я; я Икс k = –j
Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.
AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k
Уравнение плоскости
Вектор N был определен с помощью предварительно рассчитанного векторного произведения:
N = 2я -8j-2k
Следовательно, a = 2, b = -8, c = -2, искомая плоскость:
ах + по + cz + d = 0 → 2x-8y-2z + d = 0
Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:
2,4 — 8,2 — 2,1 + d = 0
Вкратце, искомая карта:
Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.
Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.
Ссылки
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
- Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
- Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
- Линии и плоскости в R 3. Получено с: math.harvard.edu.
- Нормальный вектор. Получено с сайта mathworld.wolfram.com.
Независимость Чили: история вопроса, причины, последствия
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-prjamoj-koordinaty-normalnogo-vek/
http://ru1.warbletoncouncil.org/vector-normal-6378
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Замечание 1
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
$y = kx + b$.
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ — в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos{alpha} + y cdot sin{alpha} — p = 0$
где $alpha$ — угол между прямой и осью абсцисс, а $p$ — расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
«Нормальный вектор прямой» 👇
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y — y_0 = k cdot (x — x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой — самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Определение 1
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x — x_n) + n_2 cdot (y — y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
$Ax + By + C = 0$,
то нормальный вектор описывается формулой:
$bar{n}(A; B)$.
При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
$frac{x — x_0}{p_1} = frac{y — y_0}{p_2}$
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x — x_0) + B(y — y_0) = 0$
Пример 1
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x — x_0) + B cdot (y — y_0) = 0$
Подставив значения, получаем:
$3 cdot (x — (-1)) — (-1) cdot (y — (-3)) = 0$
$3 cdot (x + 1) — (y + 3) = 0$
$3x + 3 — y — 3 = 0$
$3x — y = 0$
Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:
$3x — y = 0 implies A = 3; B = -1 implies bar{n}(A; B) = bar{n}(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x — y = 0$:
$3 cdot (-1) — (-3) = 0$
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar{p}(-B; A) implies bar{p}(1; 3)$
Ответ: $3x — y = 0; bar{p}(1; 3).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
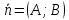
Теорема.
Алгебраическое уравнение 1-й степени
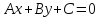
где
коэффициенты
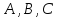
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
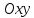
а вектор
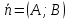
Верно
обратное:
на координатной плоскости
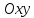
любой прямой с нормальным вектором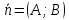
может быть записано в виде алгебраического
уравнения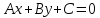
Определение.
Уравнение прямой вида
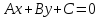
где
коэффициенты
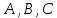
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
и
–
точки, лежащие на прямой
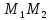
–
произвольная точка этой прямой. Тогда
векторы
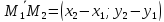
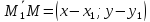
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
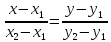
Определение.
Вектор,
параллельный прямой, называется
направляющим
вектором прямой.
Определение.
Пусть
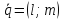
предыдущего уравнения получаемканоническое
уравнение прямой:
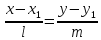
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
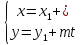
Определение.
Уравнение прямой вида
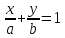
где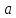
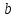
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
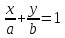
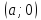
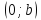
прямой с осями координат.
Определение.
Уравнение прямой вида

где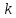
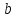
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
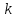
коэффициентом данной
прямой.
Теорема.
Пусть
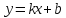
Тогда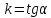
где угол
α
равен углу наклона данной прямой к оси
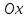
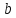
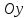
Если
известны угловые коэффициенты
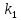
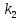
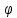
формуле:
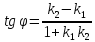
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
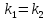
Признаком
перпендикулярности двух прямых является
соотношение:
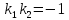
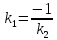
Теорема.
(Связь нормального вектора прямой с её
направляющим вектором и её угловым
коэффициентом.)
1)
Если
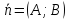
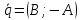
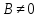
то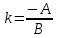
2)
Если
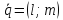
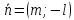
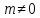
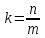
3)
Если
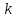
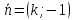
–
направляющий вектор.
Взаимное
расположение двух прямых на плоскости.
Две
прямые на плоскости могут пересекаться,
совпадать или быть параллельными.
Теорема.
Пусть прямые заданы общими уравнениями:
L1: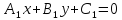
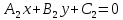
Тогда:
1)
если
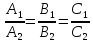
то прямые совпадают, и система уравнений
имеет
бесконечное множество решений;
2)
если
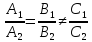
уравнений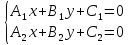
3)
если
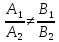
точки их пересечения являются единственным
решением системы уравнений
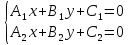
Определение.
Уравнение вида
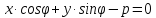
где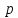
координат, называетсянормальным
уравнением прямой,
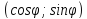
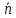
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
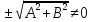
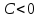
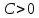
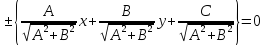
Теорема.
Орт нормального вектора
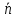
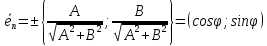
где
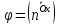
Теорема.
Расстояние от прямой до произвольной
точки
находится
по формуле:
Чтобы
найти расстояние
между двумя параллельными прямыми,
нужно взять произвольную точку на одной
из прямых и найти расстояние от нее до
другой прямой.
Чтобы
найти множество
точек, равноудаленных от двух прямых
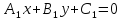
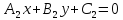
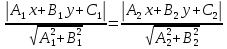
Раскрывая
модули в случае параллельных прямых,
получаем параллельную им прямую, лежащую
между данными прямыми, а в случае
пересекающихся прямых – биссектрисы
углов,
образованных пересечением прямых.
Определение.
Совокупность прямых, проходящих через
некоторую точку S,
называется пучком
прямых с центром S.
Теорема.
Если
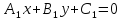
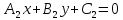
в точкеS,
то уравнение:
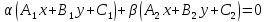
где
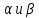
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более
того, в указанном уравнении числа всегда
возможно подобрать так, чтобы оно
определяло любую (заранее назначенную)
прямую, проходящую через точку S,
иначе говоря, любую прямую пучка с
центром S.
Поэтому уравнение вида называется
уравнением пучка с центром S.
Решение
типовых задач
Задача
№1:
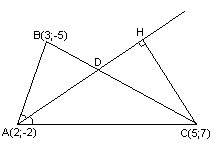
Даны
уравнения двух сторон параллелограмма
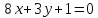
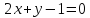
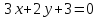
Определить координаты вершин этого
параллелограмма.
Решение:
Найдём
координаты т.
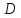
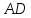
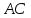
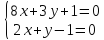
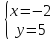
т.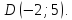
Подставим
координаты т.
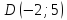
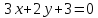
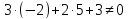
т.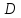
следовательно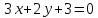
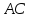
Найдём
координаты т.
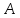
как точки пересечения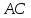
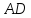
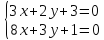
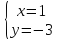
т.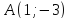
Найдём
координаты т.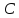
как точки пересечения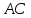
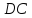
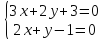

т.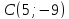
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
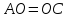
Найдём координаты т.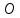
т.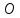
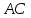
следовательно, т.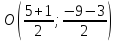
т.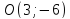
но т.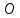
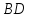
следовательно,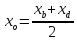
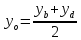
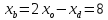
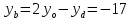
т.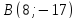
Ответ:
Задача
№2:
Дана
прямая
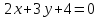
Составить уравнение прямой, проходящей
через точку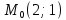
-
параллельно
данной прямой. -
перпендикулярно
к данной прямой.
Решение:
-
Искомая
прямая параллельна прямой
,
поэтому её уравнение имеет вид:.
Найдём
т.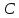
точка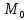
координаты удовлетворяют записанному
уравнению: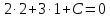
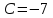
Итак, прямая принимает вид: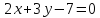
-
Т.к.
заданная и искомые прямые перпендикулярны,
то их угловые коэффициенты удовлетворяют
условию:
.
Найдём
угловой коэффициент прямой
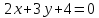
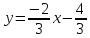
итак,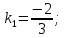
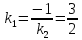
Запишем уравнение искомой прямой: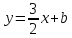
Точка
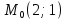
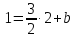
Уравнение
прямой принимает вид:
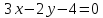
Ответ:
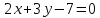
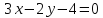
Задача
№3:
Определить,
при каких значениях a
и b
две прямые
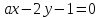
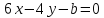
-
имеют
одну общую точку; -
параллельны;
-
совпадают.
Решение:
-
Прямые
имеют одну общую точку, когда они не
параллельны (их коэффициенты при x
и y
не пропорциональны):
;
-
Прямые
параллельны, когда коэффициенты при x
и y
пропорциональны:
;
.
-
Прямые
совпадают, когда все их коэффициенты
пропорциональны:
;
.
Задача
№4:
Найти
проекцию точки
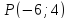
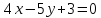
Решение:
Проведём
через т.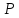
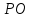
перпендикулярную прямой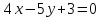
Точка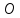
проекцией.
Прямая
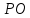
её направляющим вектором служит
нормальный вектор прямой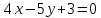
т.е.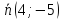
Запишем
уравнение прямой
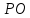
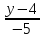
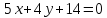
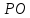
Найдём
координаты т.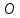
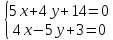
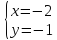
т.
Ответ:
Задача
№5:
Найти
точку
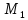
симметричную точке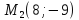
точки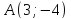
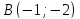
Решение:
Составим
уравнение
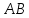
как прямой проходящей через 2 точки:
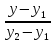
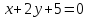
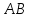
Найдём
уравнение прямой
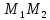
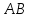
Нормальный
вектор
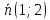
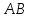
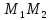
поэтому используем каноническое
уравнение прямой: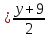
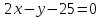
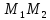
Найдём
координат т.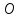
как точки пересечения прямых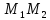
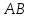
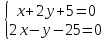
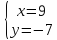
т.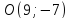
Так
как точка

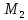
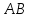
следовательно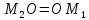
то есть т.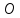
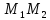
Найдём координаты точки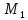
зная начало и середину отрезка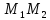
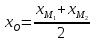
, тогда
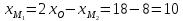
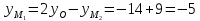
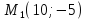
Ответ:
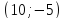
Задача
№6:
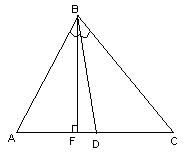
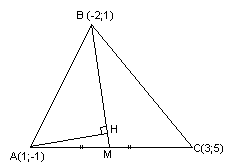
Даны
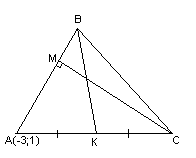
вершины треугольника
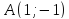
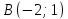
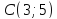
Составить уравнение перпендикуляра,
опущенного из вершины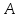
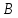
Решение:
Найдём
координаты т.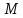
как середины отрезка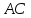
т.
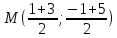
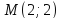
Запишем
уравнение медианы
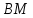
как прямой, проходящей через две известные
точки:
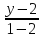
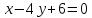
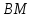
Нормальный
вектор для
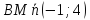
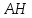
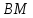
тогда уравнение примет вид:
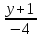
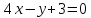
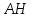
Ответ:
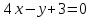
Задача
№7:
Даны
вершины треугольника

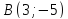
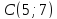
Составить уравнение перпендикуляра,
опущенного из вершины
вершине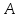
Решение:
Пусть
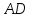
Найдём
координаты т.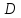
Тогда:
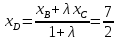
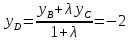
т.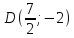
Уравнение
биссектрисы
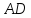
=
⇒
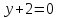
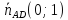
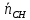
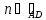
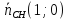
Точка
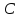
поэтому уравнение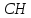
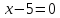
Ответ:
Задача
№8:
Две
стороны квадрата лежат на прямых
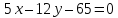
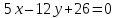
Вычислить его площадь.
Решение:
-
Выберем
на прямой
некоторую точку
:
пусть
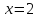
тогда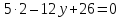
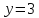
т.е.
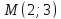
-
Найдём
расстояние от точки
до прямой
:
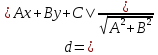
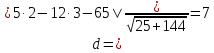
где
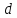
-
т.е.
.
Ответ:
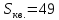
Задача
№9:
Даны
две противоположные вершины квадрата
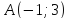
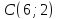
Составить уравнения его сторон.
Решение:
Зная
вершины
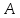

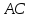
как прямой проходящей через две точки: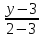
– уравнение прямой
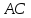
Т.к.
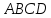
биссектрисами, поэтому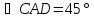
найдём угловой коэффициент
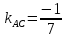
Зная
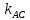

найдём угловой коэффициент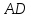
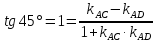
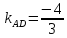
Уравнение
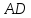
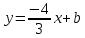
Найдём
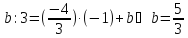
Тогда уравнение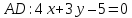
Т.к.
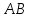
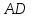
угловой коэффициент
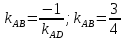
Уравнение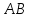
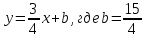
тогда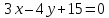
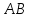
Т.к.
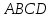
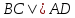
то уравнение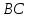
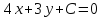
Зная,
что точка
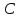
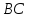
найдём свободный член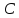
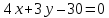
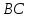
Аналогично
найдём уравнение стороны
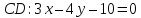
Ответ:
Задача
№10:
Вычислить
площадь треугольника, отсекаемого
прямой
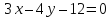
Решение:
Запишем
уравнение прямой
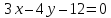
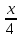
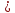
Из
этого уравнения следует, что длины
отрезков
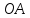
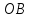
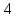
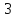
поэтому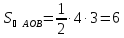
Ответ:
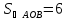
Задача
№11:
Составить
уравнения сторон треугольника, зная
одну из его вершин

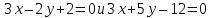
Решение:
Выясним,
что точка
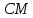
Найдём
координаты точки
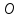
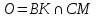
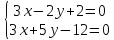
т.
Продолжим
медиану
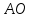
и на её продолжении отложим отрезок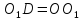
Соединим точку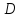
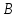
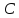
Полученный четырёхугольник
пересекаясь в точке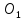
делятся пополам).
Найдём
координаты точки
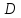
как конца отрезка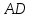

Найдём
уравнение прямой
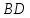
зная, что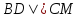

Найдём
координаты вершины
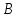
как точки пересечения прямых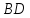
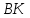
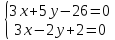
т.
Точка
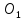
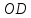
поэтому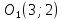
Найдём
координаты точки
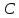
как конца отрезка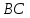
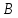
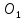
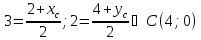
Зная
координаты всех вершин треугольника
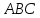
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
Задача
№12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
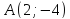
Решение:
Очевидно,
что точка

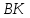
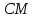
Найдём точку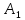
симметричную точке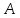
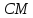
Можно доказать, что точка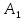
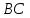
Опустим из т.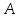
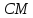
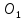
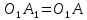
Т.к.
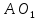
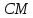
то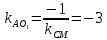
точка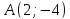
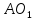
поэтому её уравнение примет вид:
Координаты
точки
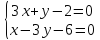
т.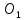
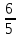
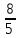
Найдём
координаты точки
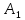
как конца отрезка
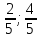
Аналогично
найдём точку
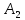
симметричную т.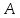
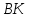
Точка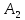
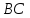
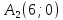
Тогда
уравнение стороны
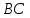
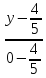
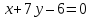
Найдём
координаты точек
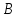
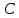
как точек пересечения прямой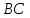
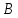
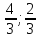
Зная
координаты вершин треугольника
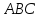
найдём уравнения его сторон.
Ответ:
Задача
№13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
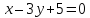
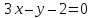
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.
Пусть
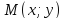
тогда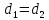
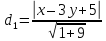
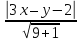
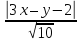
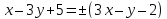
Тогда
уравнения биссектрис примут вид:
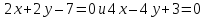
Ответ:
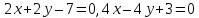
Задача
№14:
Составить
уравнение биссектрисы угла между прямыми
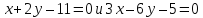
в котором лежит точка
Решение:
Найдём
отклонение точки
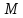
прямых, для этого приведём их уравнения
к нормальному виду: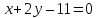
нормирующий множитель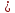
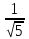
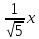
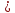
Найдём
отклонение
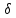
т.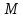
нормального уравнения подставим
координаты т.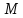
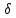
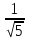
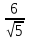
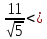
Аналогично
найдём отклонение
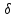
т.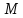
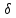
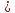
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
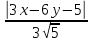
Уравнение
биссектрисы принимает вид:
Ответ:
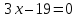
Задача
№15:
На
прямой
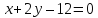
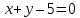
Решение:
Точки
равноудалённые от прямых
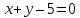
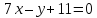
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их:
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
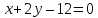
поэтому найдём их, решая системы: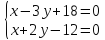
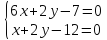
Ответ:
Задача
№16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
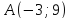
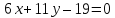
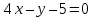
проведённых из различных вершин.
Решение:
Убедимся,
что точка
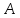
высоте.
Найдём
уравнение стороны
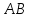
зная, что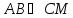
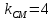
тогда уравнение примет вид:
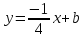
зная координаты т.
принадлежащей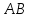
найдём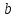
тогда уравнение примет вид: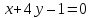
Найдём
координаты т.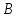
как точки пересечения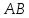
медианы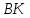
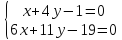
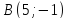
Пусть
точка
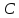
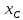
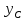
найдём их. Точка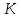
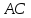
поэтому
Точка
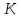
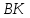
точка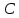
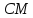
поэтому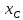
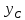
Откуда
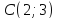
найдём уравнения всех его сторон.
Ответ:
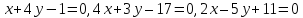
Задача
№17:
Через
точку
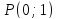
заключённый между прямыми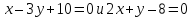
делился бы в точке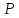
Решение:
Обозначим
через
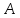
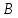
искомой прямой и пусть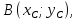
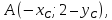
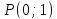
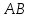
Координаты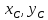
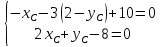
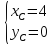
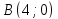
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
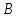
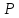
Ответ:
Задача
№18:
Составить
уравнения сторон треугольника
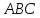
зная одну из его вершин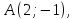
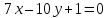
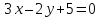
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин
Решение:
Можно
проверить, что т.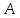
ни биссектрисе.
Найдём уравнение стороны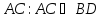
поэтому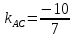
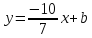
зная координаты т.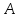
найдём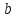
Итак,
уравнение
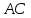
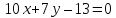
Рассмотрим
пучок с центром в т.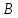
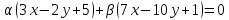
Пусть
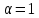
тогда уравнение пучка примет вид:
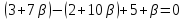
(1)
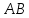
пучка, причём координаты т.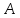
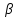
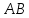
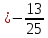
поэтому уравнение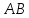
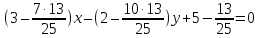
т.е.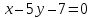
Найдём
угол между прямыми
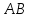
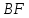
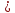
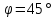
Тогда
угол
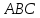
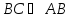
—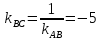
С другой стороны найдём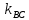
Итак,
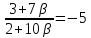
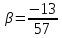
Найдём
уравнение стороны
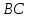
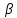
стороны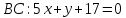
Ответ:
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.


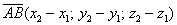
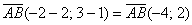
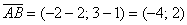







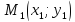
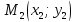
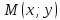


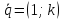
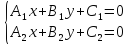
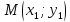
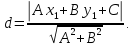

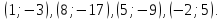
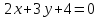 ,
,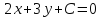 .
.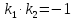 .
.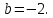
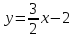
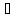
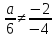 ;
;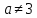
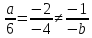 ;
;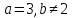 .
. ;
; .
.
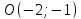
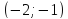
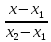
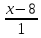
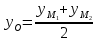
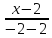
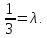
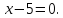
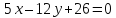 некоторую точку
некоторую точку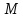 :
: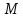 до прямой
до прямой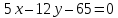 :
: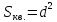 т.е.
т.е.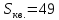 .
.