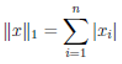Как найти нормы элементов

Нормой называют
функционал 
,
удовлетворяющий следующим аксиомам:

1. 
   ,

2. 
   ,

3. 
    (аксиома
   треугольника),

4. 
    для
   любого числа 
    (абсолютная
   однородность).

Таким
образом, норма — это полунорма, на которую
наложено дополнительное условие: норма
равна нулю только на нулевом элементе.

Нормированным
пространством называют
линейное пространство с заданной на
нём нормой.

Норму
элемента линейного пространства 
 обозначают 
.

Полное
нормированное пространство
называется банаховым
пространством.

Евклидово
пространство.
Скалярным произведением в
действительном линейном
пространстве 
 называется
функционал от двух переменных 
,
определённый для любых 
 и
удовлетворяющий следующим аксиомам:

1. 
   ,

2. 
   ,

3. 
   ,

4. 
   ,

5. 
   .

Евклидово
пространство —
это линейное пространство с заданным
в нём скалярным произведением.

В
евклидовом пространстве норма естественным
образом определяется через скалярное
произведение:

Ортогонализация —
это процесс построения ортонормированной
системы на основе линейно независимой
системы векторов.

Теорема
1 (Об ортогонализации). Рассмотрим
линейно независимую систему

элементов
евклидова пространства 
.
В пространстве 
 существует
ортогональная система элементов

,
причём каждый элемент 
 есть
линейная комбинация вида

,каждый
элемент 
 представляется
в виде
,при
этом, каждый элемент 
 определяется
с точностью до множителя 
.

Вопрос 9. Матрицы и основные действия над матрицами. Свойства действий над матрицами.

  Матрица
может состоять как из одной строки, так
и из одного столбца. Вообще говоря,
матрица может состоять даже из одного
элемента.

Определение. Если
число столбцов матрицы равно числу
строк (m=n), то матрица называетсяквадратной.

Определение. 
Матрица вида:= E,называется единичной
матрицей.

 Определение. Если a_mn = a_nm ,
то матрица называется симметрической.

Определение. Квадратная
матрица вида  называется диагональной матрицей.

Сложение
и вычитание матриц
сводится к соответствующим операциям
над их элементами. Самым главным свойством
этих операций является то, что
они определены
только для матриц одинакового размера.
Таким образом, возможно определить
операции сложения и вычитания матриц:

Определение. Суммой
(разностью) матриц
является матрица, элементами которой
являются соответственно сумма (разность)
элементов исходных матриц.

c_ij = a_ij  b_ij
С = А + В = В + А.

Операция умножения
(деления) матрицы
любого размера на произвольное число
сводится к  умножению (делению) каждого
элемента матрицы на это число.

 (А+В)
=А  В
А() = А  А 

Операция
умножения матриц

Определение: Произведением матриц
называется матрица, элементы которой
могут быть вычислены по следующим
формулам: AB = C;

Из
приведенного определения видно, что
операция умножения матриц определена
только для матриц, число
столбцов первой из которых равно числу
строк второй.

Свойства
операции умножения матриц. 

1)Умножение
матриц не
коммутативно,
т.е. АВ  ВА
даже если определены оба произведения.
Однако, если для каких – либо матриц
соотношение АВ=ВА выполняется, то такие
матрицы называютсяперестановочными.

Самым
характерным примером может служить
единичная матрица, которая является
перестановочной с любой другой матрицей
того же размера.

Перестановочными
могут быть только квадратные матрицы
одного и того же порядка.

АЕ
= ЕА = А

Очевидно,
что для любых матриц выполняются
следующее свойство: AO = O;  OA = O,

где
О – нулевая матрица.

 2)
Операция перемножения матриц ассоциативна, т.е.
если определены произведения АВ и (АВ)С,
то определены ВС и А(ВС), и выполняется
равенство: (АВ)С=А(ВС). 

3)
Операция умножения матриц дистрибутивна по
отношению к сложению, т.е. если имеют
смысл выражения  А(В+С) и (А+В)С, то
соответственно: А(В + С) = АВ + АС

(А
+ В)С = АС + ВС.

4)
Если произведение АВ определено, то для
любого числа  верно
соотношение: (AB)
= (A)B = A(B). 

5)
Если определено произведение АВ , то
определено произведение В^ТА^Т и
выполняется равенство:(АВ)^Т =
В^ТА^Т,
где индексом Т обозначается транспонированная матрица.

 6)
Заметим также, что для любых квадратных
матриц det (AB) = detAdetB.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Ирвинг Капланский

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов 

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

.

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

След 

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали: 

След обладает следующими свойствами:

• Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

• Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.

• Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

• Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

• Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Заметим, что ‖x‖₂²=xᵀx.

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

1. Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

2. f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

3. Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

4. Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

и норма l∞

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг 

Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство

для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

• Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

• Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

• Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

• Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).

Ортогональные матрицы 

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.

Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

Область значений и нуль-пространство матрицы

Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

 Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы 

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Заметим, что

• Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

  

  (или просто A > 0), а множество всех положительно определенных матриц часто обозначают

  

  .

• Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

  

  (или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

  

  .

• Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

  

• , если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.

• Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (

  

  ), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

• Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

  

  и

  

  .

Собственные значения и собственные векторы 

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

---

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

• ЗАПИСАТЬСЯ НА ДЕМОУРОК

Численные методы линейной алгебры

Основные положения численного анализа

Классическим средством изучения математических моделей и исследований на их основе свойств реальных объектов являются аналитические методы, позволяющие получать точные решения в виде математических формул. Эти методы дают наиболее полную информацию о решении задачи, и они до настоящего времени не утратили своего значения. Однако, к сожалению, класс задач, для которого они могут использоваться, весьма ограничен. Поэтому решение, как правило, осуществляется численными методами.

Численные методы — это методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям. Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой. Численные методы, в отличие от аналитических, дают не общие, а частные решения. При этом требуется выполнить достаточное количество арифметических и логических действий над числовыми и логическими массивами.

В численном анализе используются два класса численных методов:

1. Прямые методы, позволяющие найти решение за определенное число операций.

2. Итерационные методы, основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию.

Решения, получаемые численными методами, в силу их приближенности содержат некоторые погрешности. Рассмотрим их источники и типы.

Один из типов погрешностей обусловлен неадекватностью выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой. Неточность (неопределенность) задания исходных данных приводит также к неустранимым погрешностям.

Если мы устраним неопределенность в исходных данных и найдем решение с помощью какого-либо численного метода, то получим результат, не в точности соответствующий исходным данным в силу погрешности численного метода. В компьютере все числа представляются в конечном виде, и поэтому при использовании вычислительного алгоритма реализуются ошибки арифметических и других операций над числами, а также ошибки округления.

Дадим некоторые понятия из теории погрешностей вычислительных действий над приближенными величинами.

Пусть [math]x[/math] — точное, но, как правило, неизвестное значение некоторой величины, а [math]widehat{x}[/math] — ее известное приближенное значение.

Абсолютной погрешностью приближения [math]widehat{x}[/math] называется разность [math]Delta=bigl|x-widehat{x}bigr|[/math] (в общем случае [math]Deltawidehat{x}[/math] имеет размерность величины [math]x[/math]).

Относительная погрешность приближения [math]widehat{x}[/math] обозначается [math]delta[/math] и выражается отношением [math]delta= frac{Deltawidehat{x}}{|widehat{x}|}[/math] ([math]delta[/math] — безразмерная величина, [math]widehat{x}ne0[/math]). Часто величина [math]delta[/math] вычисляется в процентах, и тогда она умножается на сто.

Так как величина [math]x[/math], как правило, неизвестна, а погрешность необходимо определять, то в рассмотрение вводится предельная абсолютная погрешность [math]Delta(widehat{x}):[/math]

[math]Deltawidehat{x}= |x-widehat{x}|leqslant Delta(widehat{x}).[/math]

Раскрывая в этом неравенстве модуль, получаем соотношение, задающее отрезок, которому принадлежит точное значение: [math]widehat{x}-Delta(widehat{x}) leqslant xleqslant Delta(widehat{x})[/math]. Таким образом, величина [math]x[/math] находится в ∆-окрестности (дельта-окрестности), определяемой величинами [math]widehat{x}[/math] и [math]Delta(widehat{x})[/math].

Предельная относительная погрешность приближения [math]widehat{x}[/math] определяется отношением [math]delta(widehat{x})= frac{Delta(widehat{x})}{|widehat{x}|}[/math].

Такие погрешности оцениваются при рассмотрении численных методов. Эти оценки могут производиться до выполнения вычислений (априорные оценки) и после них (апостериорные оценки).

Как правило, численный алгоритм решения задачи завершается, если погрешность меньше заданной заранее величины.

---

Норма матриц: понятие, определение, примеры

При решении многих практических задач необходимо как-то «измерять» матрицы, чтобы говорить, что одна матрица больше другой. Правило, по которому матрице (в частности, матрице-столбцу) ставится в соответствие некоторое неотрицательное число, имеющее смысл меры, определяет понятие норма матрицы.

Нормой матрицы-столбца [math]x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}[/math] называется функция [math]|x|[/math], удовлетворяющая следующим аксиомам:

1. [math]|x|geqslant0[/math] для любого столбца [math]x[/math], причем [math]|x|=0[/math] в том и только в том случае, если [math]x[/math] — нулевой столбец;

2. [math]|alpha x|=|alpha|cdot|x|[/math] для любого действительного числа [math]alpha[/math];

3. [math]|x+y|leqslant|x|+|y|[/math] для любых двух столбцов [math]x[/math] и [math]y[/math] размеров [math](ntimes1)[/math].

Аксиома 3 называется неравенством треугольника.

Примером нормы матрицы-столбца может быть семейство норм

[math]|x|= Biggl(sum_{i=1}^{n}|x_i|^pBiggr)^{1/p},[/math]

где при любом целом положительном [math]p[/math] определяется функция, удовлетворяющая условиям 1-3.

Приведем часто используемые нормы матриц-столбцов.

1. [math]|x|_1=max_{iinmathbb{N}}|x_i|[/math] — максимум среди модулей элементов столбца;

2. [math]textstyle{|x|_2=sumlimits_{i=1}^{n}|x_i|}[/math] — сумма модулей элементов столбца;

3. [math]textstyle{|x|_3=sqrt{sumlimits_{i=1}^{n}x_i^2}}[/math] — квадратный корень из суммы квадратов элементов.

Последняя норма называется евклидовой, так как совпадает с модулем столбца (длиной вектора), т.е. [math]|x|_3=|x|=sqrt{x^Tx}[/math].

---

Замечания 10.1

1. Можно показать, что справедливы следующие соотношения

[math]|x|_2geqslant|x|_3geqslant|x|_1[/math], а также [math]sqrt{n}cdot|x|_3geqslant|x|_2,~ sqrt{n}cdot|x|_1geqslant|x|_3[/math].

2. Норма может быть использована при анализе сходимости последовательностей матриц-столбцов.

Последовательность матриц-столбцов [math]bigl{x^{(1)},x^{(2)},ldots,x^{(k)},ldotsbigr}[/math] сходится к столбцу [math]x_{ast}[/math], если [math]lim_{kto+infty}x_i^{(k)}=x_{ast i}[/math], для всех [math]i=1,2,ldots,n[/math]. Для того чтобы последовательность [math]bigl{x^{(1)},x^{(2)}, ldots,x^{(k)},ldotsbigr}[/math] сходилась к столбцу х., необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|x^{(k)}-x_{ast}bigr|=0[/math].

3. Для определения псевдорешений систем линейных алгебраических уравнений ранее использовалась евклидова норма [math]|x|_3[/math].

4. Нормы позволяют оценить скорость сходимости последовательностей. Рассмотрим последовательность [math]bigl{x^{(k)}bigr}[/math], сходящуюся к [math]x_{ast}[/math]. Предположим, что все ее элементы различны и ни один из них не совпадает с [math]x_{ast}[/math]. Наиболее эффективный способ оценивания скорости сходимости состоит в сопоставлении расстояния [math]bigl|x^{(k+1)}-x_{ast}bigr|[/math] между [math]x^{(k+1)}[/math] и [math]x_{ast}[/math] с расстоянием [math]bigl|x^{(k)}-x_{ast}bigr|[/math] между [math]x^{(k)}[/math] и [math]x_{ast}[/math].

Последовательность [math]bigl{x^{(k)}bigr}[/math] называется сходящейся с порядком [math]{p}[/math], если [math]{p}[/math] — максимальное число, для которого

[math]0leqslant lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p} < +infty.[/math]

Поскольку величина [math]{p}[/math] определяется предельными свойствами [math]bigl{x^{(k)}bigr}[/math], она называется асимптотической скоростью сходимости.

Если последовательность [math]bigl{x^{(k)}bigr}[/math] — сходящаяся с порядком [math]{p}[/math], то число

[math]c=lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p},.[/math]

называется асимптотическим параметром ошибки. Если [math]p=1,~ c<1[/math], то сходимость линейная, если [math]p=2[/math] — квадратичная, если [math]p=3[/math] — кубическая и т.д. Если [math]p>1[/math] или [math]p=1,~c=0[/math], то сходимость сверхлинейная. Линейная сходимость является синонимом сходимости со скоростью геометрической профессии. Сверхлинейная сходимость является более быстрой, чем определяемая любой геометрической прогрессией.

Пример 10.1. Вычислить нормы матрицы-столбца [math]x=begin{pmatrix} 1&-2&3&-4 end{pmatrix}^T[/math].

Решение.

[math]begin{aligned} mathsf{1)}~, |x|_1&= max_{iinmathbb{N}}|x_i|= maxbigl{|1|,|-2|,|3|,|-4|bigr}=4,;\[5pt] mathsf{2)}~, |x|_2&= sum_{i=1}^{4}|x_i|= |1|+|-2|+|3|+|-4|=10,;\[5pt] mathsf{3)}~, |x|_3&= sqrt{sum_{i=1}^{4}x_i^2}= sqrt{1^2+(-2)^2+3^2+(-4)^2}=sqrt{30},. end{aligned}[/math]

Заметим, что свойство [math]|x|_2geqslant|x|_3geqslant|x|_1[/math], очевидно, выполняется.

---

Пусть [math]A[/math] — произвольная матрица размеров [math](mtimes n)[/math].

Нормой матрицы [math]A[/math] называется функция [math]|A|[/math], удовлетворяющая следующим аксиомам:

1) [math]|A|geqslant0[/math] для любой матрицы [math]A[/math], причем [math]|A|=0[/math] в том и только в том случае, если [math]A[/math] — нулевая матрица;

2) [math]|alphacdot A|=|alpha|cdot|A|[/math] для любого действительного числа [math]alpha[/math];

3) [math]|A+B|leqslant|A|+|B|[/math] для любых двух матриц [math]A[/math] и [math]B[/math] размеров [math](mtimes n)[/math] (неравенство треугольника);

4) [math]|Acdot B|leqslant|A|cdot|B|[/math] для любых двух матриц, у которых определено произведение.

Матричные нормы удобно определять через нормы матриц-столбцов. Для этого, задавшись какой-нибудь нормой для матриц-столбцов, рассматриваются значения [math]|Ax|[/math] при всевозможных х, удовлетворяющих условию [math]|x|=1[/math]. Максимальное из этих значений, которое найдется всегда, берется в качестве нормы матрицы [math]Acolon, |A|= max_{|x|=1}|Ax|[/math]. Такую матричную норму называют индуцированной.

Заметим, что в качестве определения индуцированной матричной нормы часто используется выражение [math]|A|=sup_{xne0}frac{|Ax|}{|x|}[/math], характеризующее максимальную величину, на которую преобразование, описываемое матрицей [math]A[/math], может растянуть любой ненулевой вектор в заданной норме.

Наиболее употребительными являются следующие формулы для вычисления значений норм матриц с действительными элементами.

1) [math]textstyle{|A|_1= maxlimits_{1leqslant ileqslant m}sumlimits_{j=1}^{n}|a_{ij}|}[/math] — максимум суммы модулей элементов в строке;

2) [math]textstyle{|A|_2= maxlimits_{1leqslant jleqslant n}sumlimits_{i=1}^{m}|a_{ij}|}[/math] максимум суммы модулей элементов в столбце;

3) [math]|A|_3=sqrt{lambda_{max}(A^TA)}[/math] — квадратный корень из максимального собственного значения [math]lambda_i[/math] матрицы [math]A^TA[/math];

4) [math]textstyle{|A|_4= sqrt{sumlimits_{i=1}^{m} sumlimits_{j=1}^{n} a_{ij}^2}}[/math] — квадратный корень из суммы квадратов элементов.

Заметим, что вычисление нормы [math]|A|_3= sqrt{lambda_{max}(A^TA)}[/math] связано с весьма трудоемкими операциями. Поскольку справедливо неравенство

[math]|A|_3=sqrt{lambda_{max}(A^TA)} leqslant |A|_4= sqrt{sumlimits_{i=1}^{m} sum_{j=1}^{n} a_{ij}^2},[/math]

то норма [math]|A|_4[/math] часто используется в оценках вместо [math]|A|_3[/math]. Норма [math]|A|_4[/math] возникает, если матрице [math]A[/math] поставить в соответствие «длинный столбец»:

[math]begin{pmatrix}a_{11},a_{21},ldots, a_{m1},a_{12},a_{22},ldots, a_{m2},ldots,a_{nn} end{pmatrix}^T[/math] и применить норму [math]|x|_3[/math].

---

Пример 10.2. Вычислить нормы матриц [math]A=begin{pmatrix}1&-2&3\ 4&5&-6\ -7&8&9 end{pmatrix}!,~ B=begin{pmatrix}1&0&0\ 0&1&0\ 0&0&1 end{pmatrix}[/math].

Решение. а)

[math]begin{aligned}|A|_1&= maxbigl{|1|+|-2|+|3|;, |4|+|5|+|-6|;, |-7|+|8|+|9|bigr}= max{6;,15;,24}=24;\[5pt] |A|_2&= maxbigl{|1|+|4|+|-7|;, |-2|+|5|+|8|;, |3|+|-6|+|9|bigr}= max{12;15;18}=18;\[5pt] |A|_4&= sqrt{1^2+(-2)^2+3^2+4^2+5^2+(-6)^2+(-7)^2+8^2+9^2}=\[2pt] &=sqrt{1+4+9+16+25+36+49+64+81}= sqrt{285};end{aligned}[/math]

б) [math]|B|_1=|B|_2=1,,~ |B|_4=sqrt{1+1+1}=sqrt{3}[/math].

---

Норма матриц может быть использована при анализе сходимости различных численных процедур. Пусть имеется последовательность матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] размеров [math]mtimes n[/math]. Матрица [math]A[/math] называется пределом последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math], если [math]lim_{kto+infty}a_{ij}^{(k)}=a_{ij}[/math] для всех [math]i=1,ldots,m[/math] и [math]j=1,ldots,n[/math]. Это обозначается [math]lim_{kto+infty}A^{(k)}=A[/math].

Для сходимости последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] к матрице [math]A[/math] необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|A^{(k)}-Abigr|=0[/math]. При этом последовательность, составленная из норм матриц [math]A^{(k)}[/math], сходится к норме матрицы [math]A[/math], т.е. [math]lim_{kto+infty} bigl|A^{(k)}bigr|=|A|[/math].

Отметим некоторые свойства предела матриц. Если [math]lim_{kto +infty}A^{(k)}=A,~ lim_{kto+infty}B^{(k)}=B[/math], то:

[math]begin{array}{ll}mathsf{1)}~ limlimits_{kto+infty}bigl[A^{(k)}pm B^{(k)}bigr]=Apm B;&qquad mathsf{2)}~ limlimits_{kto+infty}bigl[A^{(k)}cdot B^{(k)}bigr]=Acdot B;\\[-5pt] mathsf{3)}~ limlimits_{kto+infty}bigl[A^{(k)}bigr]^{-1}=A^{-1};&qquad mathsf{4)}~ limlimits_{kto+infty}bigl[CA^{(k)}bigr]=CA,~ limlimits_{kto+infty}bigl[A^{(k)}Dbigr]=AD.end{array}[/math]

где считается, что все операции определены.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.