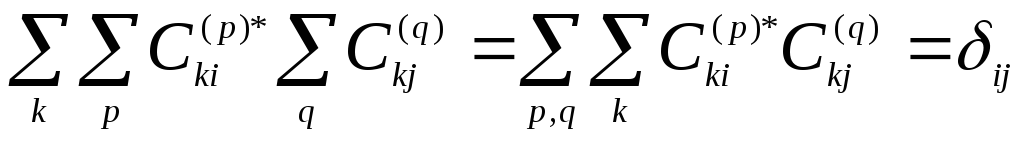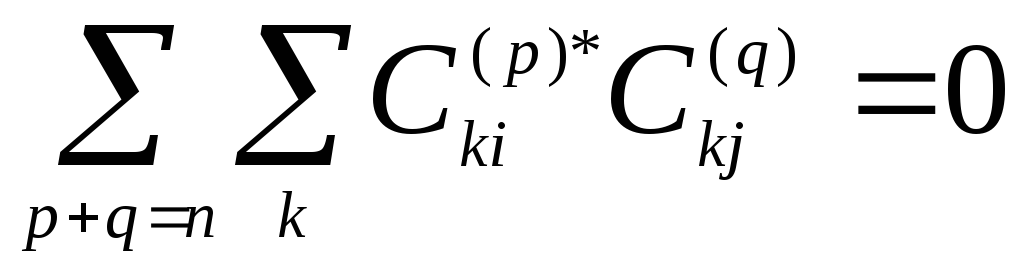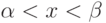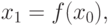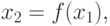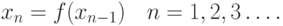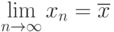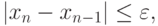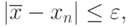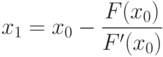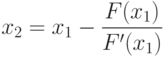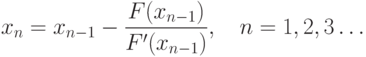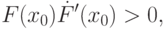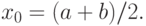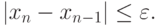Рассмотрим
оператор
,
который обладает дискретным спектром:
Под
номером
понимается набор всех квантовых чисел,
опереляющих состояние системы.
—
значения образующие энергетический
спектр.
Так
как спектр невырожденный, то между
состоянием и уровнем (энергией) существует
взаимооднозначное соответствие, т. е.:
.
Т.
к. спектр дискретный, то функции
квадратичноинтегрируемы:
/
Пусть
ЗШЛ решена и найдены собственные функции
и собственные значения
.
Рассмотрим
ЗШЛ:
.
Оператор
здесь имеет такую структуру, что эта
ЗШЛ просто не решается, как ЗШЛ для
оператора.
Оператор
должен:
-
иметь
структуру
,
где— оператор для которого задача решена.,
— дает малую добавку в оператор.
-
Спектр
собственных функций дискретен, тогда
собственные функции квадратичноимнтегрируемые
.
Решим задачу
разложения по малому параметру (через
теорию возмущений).
Из этого получаем
(*)
т.к.
параметр
малый, то энергетический спектр можно
разложить по малому параметру:
p
– указывает
порядок разложения и показывает малость
члена суммы.
отвечает
невозмущенной задаче
.
—
поправка имеющая первый порядок малости.
Т.
к. собственные функции оператора
образуют базис, то по ним можно разложить
собственные функции возмущенного
оператора
.
(**)
Коэффициенты
разложения:
Их
можно разложить по малому параметру:
Теперь
задача теории возмущений состоит в
нахождении членов рядов:
(***)
Чем
больше членов рядов найдем, тем точнее
решим задачу.
Подставим
(**) в (*) и вынесем коэффициенты за знак
операторов
Используем
решение для невозмущенного оператора
Обозначим
этот ряд
,
где,
тогда
.
Используем
соотношение
.
Коэффициенты
выносятся за знак скалярного произведения:
Рассчитаем
.
—
это матричный элемент оператора
возмущений, который рассчитывается по
невозмущенным функциям.
Тогда
имеем
.
Получили
матричное уравнение, которое должны
разложить по малым параметрам и прировнять
0 все слагаемые соответствующие своим
порядкам малости.
считается величиной первого порядка
малости, по нему проводится разложение.
Используем,
что
,
здесь
Тогда
(4*)
Получили
исходное уравнение. К нему еще добавляются
две нормировки:
,
(1)
(2)
Подставим
в уравнение (4*) выражения (***)
(3)
Группируем
члены по порядку малости. По каждому
порядку должны получать справа ноль.
Сначала
нулевой порядок
Так
как
имеет первый порядок малости то член
связанный с ним будет отсутствовать.
Из
этого выражения получаем что, так как
спектр невырожденный, при
дает
и получаем
,
а при,
может быть
.
Легко
видеть, что так как
,
то
нулевое приближение дает
.
Тогда
в нулевом приближении имеем решение:
Теперь
для уровней:
.
Окончательно
в результате нулевого приближения
Перейдем
к первому приближению.
Получим
дополнительные соотношения из условия
нормировки возмущенных функций.
Так
как
,
,
получим
.
Подставим
сюда разложение по малому параметру
,
тогда
имеем
Здесь
справа стоит величина нулевого порядка
малости.
Для
,
.
Для
(5*)
Рассмотрим
первое приближение:
.
Два случая
и
,
и
.
(6*)
Из
(5*) имеем

Используем,
что
Тогда
из (6*) и (7*):
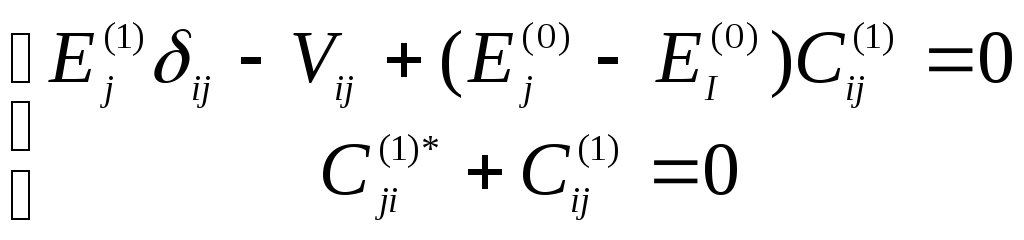
Из
(8*) рассмотрим случай
:
—
поправка к i-ому
энергетическому уровню первого порядка
малости
Тогда
в первом приближении
и
также получаем
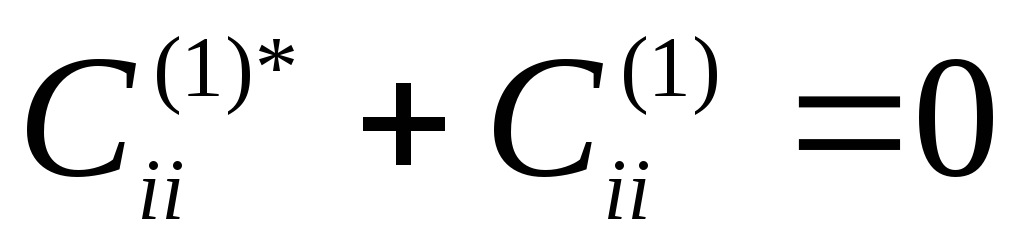
Тогда
получили, что
,
т.
е. коэффициенты
чисто мнимые.
Ввиду
неопределенности фазового множителя
при волновой функции, то полагают
,
тогда
принимают
.
Из
(8*) рассмотрим случай
.
.
Подставим
это выражение в (8*) и проверим условие
нормировки:

Распишем
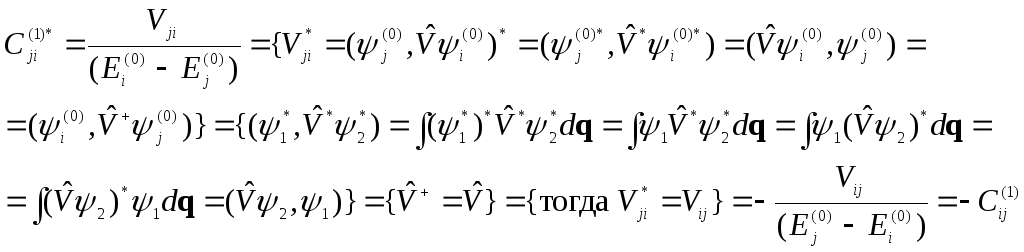
истинность условия нормировки.
Тогда
в первом приближении теории возмущений
получили:
.
Нам
необходимо найти волновые функции, для
них
Метод итераций решения системы уравнений. Пример решения
Решение получаем с помощью калькулятора Решение СЛАУ методом итераций .
Достаточное условие сходимости метода простых итераций
Прежде чем применять метод итераций, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы. Если при этом условие все таки не выполняется, то иногда удается обеспечить сходимость метода с помощью следующего метода.
Пусть дана система Ax = b. Преобразуем ее к виду: x= Qx + c
где Q = E — D•A, c = D•b
Здесь D — некоторая матрица. Нам необходимо подобрать такую матрицу D, чтобы выполнялось условие |Q| 0 =β, тогда:
x 1 =b — a x 0
x 2 =b — a x 1
.
x k+1 =b — a x k
Для нашей задачи достаточное условие сходимости выполняется.
Приведем к виду:
x1=0.5-(0.2x2-0.1x3)
x2=-4.07-(0.33x1+0.17x3)
x3=3-(0.0833x1-0.25x2)
Покажем вычисления на примере нескольких итераций.
N=1
x1=0.5 — 0 • 0.2 — 0 • (-0.1)=0.5
x2=-4.07 — 0 • 0.33 — 0 • 0.17=-4.07
x3=3 — 0 • 0.0833 — 0 • (-0.25)=3
N=2
x1=0.5 — (-4.07) • 0.2 — 3 • (-0.1)=1.61
x2=-4.07 — 0.5 • 0.33 — 3 • 0.17=-4.74
x3=3 — 0.5 • 0.0833 — (-4.07) • (-0.25)=1.94
N=3
x1=0.5 — (-4.74) • 0.2 — 1.94 • (-0.1)=1.64
x2=-4.07 — 1.61 • 0.33 — 1.94 • 0.17=-4.93
x3=3 — 1.61 • 0.0833 — (-4.74) • (-0.25)=1.68
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | x3 | e1 | e2 | e3 |
| 0 | 0 | 0 | 0 | |||
| 1 | 0.5 | -4.07 | 3 | 0.5 | 4.07 | 3 |
| 2 | 1.61 | -4.74 | 1.94 | 1.11 | 0.67 | -1.06 |
| 3 | 1.64 | -4.93 | 1.68 | 0.0274 | 0.19 | -0.26 |
| 4 | 1.65 | -4.9 | 1.63 | 0.013 | -0.0341 | -0.051 |
| 5 | 1.64 | -4.89 | 1.64 | -0.0119 | -0.00416 | 0.00744 |
| 6 | 1.64 | -4.89 | 1.64 | -8.8E-5 | -0.00273 | 0.00203 |
| 7 | 1.64 | -4.89 | 1.64 | -0.000343 | 0.00031 | 0.000691 |
Ответ: x1=1.64, x2=-4.89, x3=1.64
Пример №2 . Решить систему уравнений Ax = b с точностью 0.05 методами: 1) простой итерации; 2) Зейделя. Указание. Для обеспечения выполнения достаточного условия сходимости воспользоваться перестановкой строк в исходной системе уравнений.
Итерационные методы решения системы линейных алгебраических уравнений
В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
Общие сведения об итерационных методах или методе простой итерации
Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .
Рассмотрим систему A x = b .
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.
Метод Якоби
Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.
Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
b i j = — a i j / a i i , i , j = 1 , 2 . . . , n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
d i = b i / a i i , i = 1 , 2 , . . . , n
Расчетная формула метода простой итерации:
x ( n + 1 ) = B x ( x ) + d
Матричная запись (координатная):
x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b
Критерий окончания в методе Якоби:
x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε
В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:
x ( n + 1 ) — x ( n ) ε
Решить СЛАУ методом Якоби:
10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10
Необходимо решить систему с показателем точности ε = 10 — 3 .
Приводим СЛАУ к удобному виду для итерации:
x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1
Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01
Аналогичным способом вычисляются приближения к решению:
x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111
Находим норму матрицы В , для этого используем норму B ∞ .
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:
x ( n + 1 ) — x ( n ) ε
Далее вычисляем нормы разности векторов:
x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .
Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.
x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .
Метод Зейделя
Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.
x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +
+ . . . + b i m x m ( n ) + d i
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Решим 3 системы уравнений:
2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1
Приведем системы к удобному для итерации виду:
x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .
Отличительная особенность, условие сходимости выполнено только для первой системы:
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109
Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.
2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129
Итерационный процесс разошелся.
Решение: x 1 = 1 , x 2 = 2
3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2
Итерационный процесс зациклился.
Решение: x 1 = 1 , x 1 = 2
Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x = x — τ ( A x — b ) , τ — итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .
Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .
Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .
τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .
Итерационные методы решения СЛАУ
Вы будете перенаправлены на Автор24
Для решения систем линейных уравнений используется два основных метода решений, прямые методы, также называемые точными и итерационные методы, при использовании которых ответ в любом случае будет приближённым.
Особенность прямых методов состоит в том, что вычисления в них всегда проводятся точно, например, с использованием целых чисел, но при этом эти методы трудно применимы для вычисления решений для больших систем. К прямому методу относится, например, метод Крамера.
Ниже подробно рассмотрены итерационные методы решения СЛАУ.
Сущность итерационных методов решения систем линейных уравнений
Как уже отмечалось выше, итерационные методы в принципе являются приближёнными. Их сущность состоит в том, что сначала записывается некоторая последовательность столбцов матрицы, после чего производится поочередное вычисление каждого столбца. Каждый новый столбец вычисляется на основе вычисленных предыдущих, при этом с каждым вычислением получается всё более точное приближение искомого решения. Когда достигнута необходимая точность, процесс вычисления прерывают и в качестве решения используют последний вычисленный столбец.
Процесс вычисления одного столбца называется итерацией.
Различают несколько основных способов итерационного решения СЛАУ:
Метод Якоби (метод простых итераций СЛАУ)
Рассмотрим систему уравнений, с коэффициентами, которые можно записать в виде матрицы:
$A=left(begin a_ <11>& a_ <12>& … & a_ <1n>\ a_ <21>& a_ <22>& … & a_ <2n>\ … & … & … & … \ a_ & a_ & … & a_ \ endright)$
Саму же систему уравнений можно записать в виде равенства $A cdot X = F$, где $X$ — вектор-столбец собственных значений системы, а $F$ — вектор-столбец свободных членов.
Метод состоит в том, чтобы в каждом уравнении системы выразить соответственно $x_1, x_2,…, x_n$ и затем получить новую матрицу $B$, у которой элементы главной диагонали принимают нулевые значения.
В общем виде формула для вычисления корней уравнений записывается так: $overrightarrow= Boverrightarrow + overrightarrow$
Добиться такого вида от системы можно следующими способами:
Готовые работы на аналогичную тему
$B= E – D^<-1>A=D^<-1>(D-A), overrightarrow = D^<-1>overrightarrow;$
Здесь $D$ — матрица, у которой нулевые все элементы, кроме элементов на главной диагонали, а на главной диагонали находятся соответствующие элементы матрицы $A$. Матрицы $U$ и $L$ означают верхнетреугольную матрицу и нижнетреугольную соответственно; их значимые элементы соответствуют частям матрицы $A$. Буквой $Е$ же обозначается единичная матрица соответствующей размерности.
Процедура нахождения корней тогда запишется так:
$overrightarrow^<(k+1)>= Boverrightarrow^ <(k)>+ overrightarrow$
Для конкретного элемента она будет выглядеть так:
$x_^=frac<1>(b_i — sumlimits_ a_ijcdot x_j^(k)left(1right)$, где $i=1,2,…, n$
буквой $(k)$ во всех формулах выше обозначается номер итерации, сама же формула $(1)$ называется рекуррентной.
Окончание вычисления происходит в том случае, если разница между вычислениями в двух соседних итераций составляет не более чем $ε_1$:
В упрощённой форме условие окончания итераций выглядит как $||x^<(n+1)>-x^<(n)>||$
Порядок решения СЛАУ методом Якоби такой:
- Приведение системы уравнений к виду, в котором на каждой строчке выражено какое-либо неизвестное значение системы.
- Произвольный выбор нулевого решения, в качестве него можно взять вектор-столбец свободных членов.
- Производим подстановку произвольного нулевого решения в систему уравнений, полученную под пунктом 1.
- Осуществление дополнительных итераций, для каждой из которых используется решение, полученное на предыдущем этапе.
Метод Гаусса-Зейделя
Сущность этого метода состоит в том, что в нём переносятся в правые части все члены уравнений, индекс при которых больше индекса, выражаемого $x$. В краткой форме это можно записать так:
$(L + D) cdot overrightarrow = -Uoverrightarrow + overrightarrow$
Сами итерации в методе Гаусса-Зейделя производятся по формуле:
$(L +D)overrightarrow^<(k+1)>=-Uoverrightarrow^ <(k)>+ overrightarrow$
Метод Гаусса-Зейделя похож на метод Якоби, но здесь полученные значения переменных используются не исключительно для следующей итерации, а сразу для следующего вычисления значения $x$.
Метод простых итераций: пример решения
Дана система уравнений:
$begin 10x_1 – x_2 + 2x_3 = 6 \ -x_1 + 11x_2 – x_3 + 3x_4 = 25 \ 2x_1- x_2 + 10x_3 -x_4 = -11 \ 3x_2 – x_3 + 8x_4 = 15 end$
Решите данную систему с помощью метода простых итераций.
Выберем в качестве нулевого приближения корни $(0; 0; 0; 0)$ и подставим их в преобразованную систему:
$begin x_1 = (6 + 0 – (2 cdot 0))/10 = 0,6 \ x_2 = (25 + 0 – 0 – (3 cdot 0))/11 = 25/11 = 2,2727 // x_3 = (-11 – (2 cdot 0) + 0 + 0) /10 = -1,1 \ x_4 = (15 – (3 cdot 0) + 0) / 8 = 1,875\ end$
Проведём 5 итераций, используя на каждой результат, полученный с предыдущей и для них получим следующую таблицу:
Рисунок 1. Таблица итераций для решения СЛАУ. Автор24 — интернет-биржа студенческих работ
Продолжать вычисление можно до достижения заданной требуемой точности. Точный ответ системы — $(1; 2; -1; 1)$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13.02.2022
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/iteratsionnye-metody-reshenija-slau/
http://spravochnick.ru/matematika/iteracionnye_metody_resheniya_slau/
Задание 1. Указатели
Решите уравнение указанным в варианте методом. Функцию передать как параметр с помощью указателя.
Численные методы решения уравнений
Довольно часто на практике приходится решать уравнения вида:
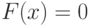 |
( 2) |
где функция 
Всякое значение 

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Поэтому важное значение приобрели численные методы, позволяющие найти приближенное значение корня. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет компьютер.
Существует множество численных методов решения уравнений вида (1). Рассмотрим только три из них:
- метод итераций;
- метод Ньютона;
- метод половинного деления.
Метод итераций
Представим уравнение 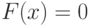
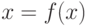 |
( 2) |
Это уравнение получается выделением 




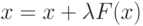 |
( 3) |
где 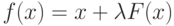
На заданном отрезке ![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)
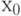
потом найдем:
Таким образом, процесс нахождения корня уравнения сводится к последовательному вычислению чисел:
Этот процесс называется методом итераций.
Если на отрезке ![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)
то процесс итераций сходится, т.е.
Процесс итераций продолжается до тех пор, пока
где – 

Метод Ньютона
Пусть уравнение 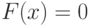
![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)


![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)
Выберем на отрезке ![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)
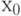
потом
Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел 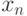
Этот процесс называется методом Ньютона.
Процесс вычисления продолжается до тех пор, пока не будет выполнено условие:
где – 

Точку 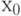
иначе метод не будет сходиться.
Метод половинного деления
Пусть уравнение 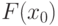
![[a, b]](https://intuit.ru/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png)
![[a, b]](https://intuit.ru/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png)
Метод половинного деления заключается в следующем:
Сначала выбираем начальное приближение, деля отрезок пополам, т.е.
Если 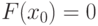

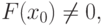
Процесс деления отрезка продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданной точности 
Варианты задания
| № | Уравнение | Отрезок, содержащий корень | Метод | Значение корня с точностью 10-4 |
|---|---|---|---|---|
| 1 |  |
[2;3] | Итераций | 2,2985 |
| 2 |  |
[0;2] | Ньютона | 1,0001 |
| 3 |  |
[0;0,85] | Итераций | 0,2624 |
| 4 | 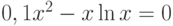 |
[1;2] | Ньютона | 1,1183 |
| 5 | 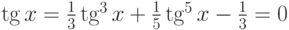 |
[0;8] | Половинного деления | 0,3333 |
| 6 | 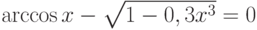 |
[0;1] | Итераций | 0,5629 |
| 7 | 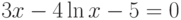 |
[2;4] | Ньютона | 3,2300 |
| 8 |  |
[1;2] | Половинного деления | 1,8756 |
| 9 | 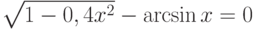 |
[0;1] | Итераций | 0,7672 |
| 10 | 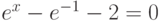 |
[0;1] | Ньютона | 0,8814 |
| 11 | 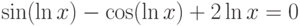 |
[1;3] | Половинного деления | 1,3749 |
| 12 |  |
[1,2;2] | Итераций | 1,3077 |
| 13 | 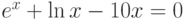 |
[3;4] | Ньютона | 3,5265 |
| 14 | 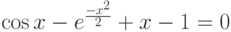 |
[1;2] | Половинного деления | 1,0804 |
| 15 | 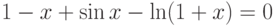 |
[0;1,5] | Итераций | 1,1474 |
| 16 | 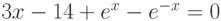 |
[1;3] | Ньютона | 2,0692 |
| 17 |  |
[0;1] | Половинного деления | 0,5768 |
| 18 |  |
[0,5;1] | Итераций | 0,9892 |
| 19 | 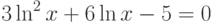 |
[1;3] | Ньютона | 1,8832 |
| 20 | 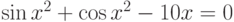 |
[0;1] | Половинного деления | 0,1010 |
| 21 | 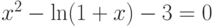 |
[2;3] | Итераций | 2,0267 |
| 22 | 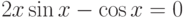 |
[0,4;1] | Ньютона | 0,6533 |
| 23 |  |
[-1;0] | Половинного деления | -0,2877 |
| 24 | 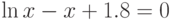 |
[2;3] | Итераций | 2,8459 |
| 25 | ![sqrt[3]{x-4}-frac{1}{x^2+1}=0](https://intuit.ru/sites/default/files/tex_cache/939eb1b356d8b63b4bd66093c15b561c.png) |
[4;6] | Ньютона | 4,0002 |
| 26 | 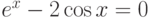 |
[0;2] | Половинного деления | 0,5398 |
| 27 | ![sqrt[3]{x+2}-3x+16=0](https://intuit.ru/sites/default/files/tex_cache/2ca12f8dd1d3c8e29468546b3019b01f.png) |
[4;7] | Итераций | 6,0000 |
| 28 |  |
[1;2] | Ньютона | 1,5708 |
Нулевое приближение
Cтраница 1
Нулевое приближение полностью совпадает с решением для кругового отверстия.
[1]
Нулевое приближение совпадает с решением для цилиндрической оболочки.
[2]
Нулевое приближение К0 ( t) в формуле ( 111 134) выбирается произвольно.
[3]
Нулевые приближения для УА принимаем в предположении линейного изменения У А в зависимости от z; для t — равными граничному значению: / i 70 С; для О — равными 67 С ( соответствует температуре динамического равновесия), за исключением точки 21, для которой ft равно граничному значению Ь 50 С.
[4]
Нулевое приближение совпадает с решением задачи о колебаниях вращения абсолютно жесткого шара в упругой среде.
[5]
Нулевое приближение строится следующим образом.
[6]
Найденное нулевое приближение еще очень далеко от реальной характеристики молекулы.
[7]
Традиционно нулевое приближение для решения задачи ОМП находится графическим способом, если другая информация отсутствует. За нулевое приближение принимаются координаты точки пересечения двух линий положения. Затем решение уточняется по итерационной процедуре с использованием линейного алгоритма. Недостаток такой схемы заключается в том, что построение линий положения и определение координат точки их пересечения требует большого числа вычислительных операций.
[8]
Нулевое приближение ФМП НТП объединяет обе указанные идеализации в рамках модели идеального газа ядер и электронов, определенного для случая любых температур и концентраций.
[9]
Нулевые приближения наивыгоднейших нагрузок электростанций, соответствующие неучету влияния сети, будут: Р0 50 Мет, PI 50 Мет.
[11]
Нулевым приближением для реальных жидких или твердых растворов является идеальный равтвор.
[12]
Нулевым приближением для реальных жидких или твердых растворов является идеальный раотвор.
[13]
Нулевым приближением в этой задаче являются собственные функции и собственные значения уравнения Шредингера для электрона в атоме водорода.
[14]
Нулевым приближением ( ф), 90) Д ( 0) здесь является задача (45.1) — (45.3) о возмущениях при нулевой разности температур между плоскостями ( g 0); она дает невозмущенный спектр амплитуд и декрементов. Поправки к амплитудам и декрементам, возникающие при отличной от нуля ( но достаточно малой) разности температур, получаются путем решения уравнений последовательных приближений. В каждом порядке приходится решать неоднородную задачу, условие разрешимости которой дает соответствующую поправку к декременту. Амплитуды ф ( л, 9п удобно искать в виде разложений по невозмущенным амплитудам.
[15]
Страницы:
1
2
3
4