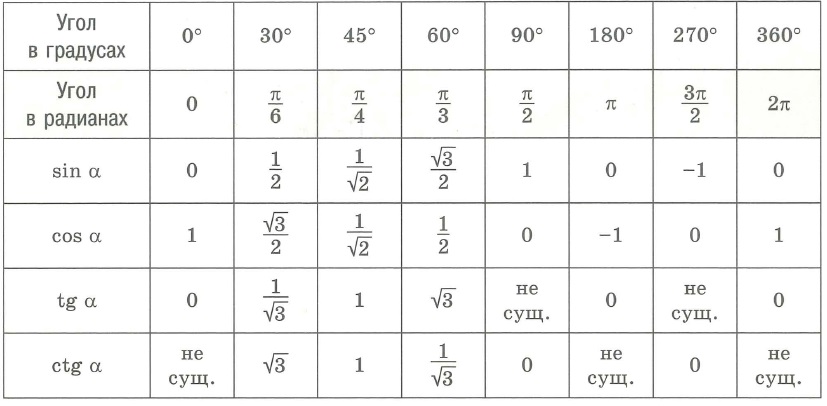
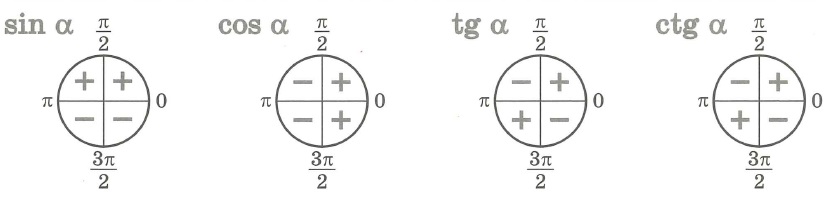
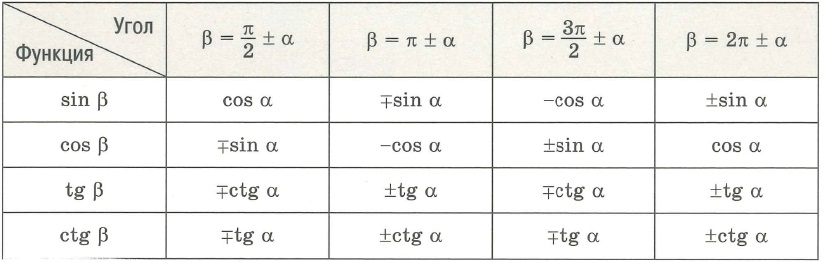
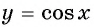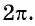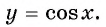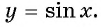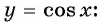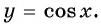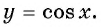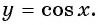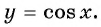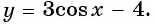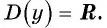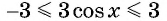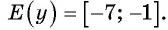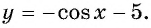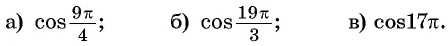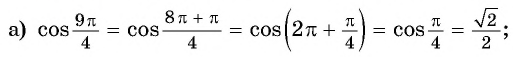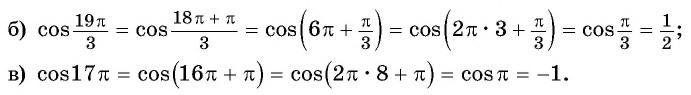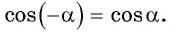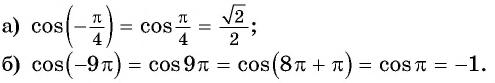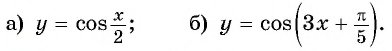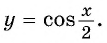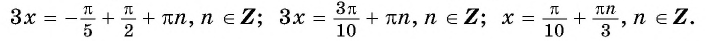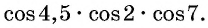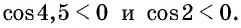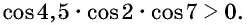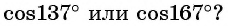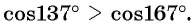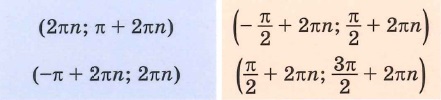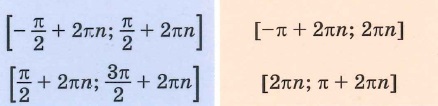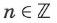Функция
y=cosx
определена на всей числовой прямой, и множеством её значений является отрезок
−1;1
.
Поэтому её график не выходит за границы полосы между прямыми
y=−1
и
y=1
.
Используя свойство периодичности функции
y=cosx
, можно построить её график на промежутке
−π≤x≤π
длиной
2π
и повторить несколько периодов с такими же значениями.
Функция
y=cosx
— чётная. Её график симметричен относительно оси (Oy).
Построим график функции на промежутке
−π≤x≤π
. Так как функция
y=cosx
является чётной, можно построить график на промежутке
0≤x≤π
, а потом симметрично отобразить относительно оси (Oy).
Значения функции в удобных точках на этом отрезке
0≤x≤π
равны:
cos0=1;cosπ6=32;cosπ4=22;cosπ3=12;cosπ2=0;cosπ=−1
.
Учитывая периодичность функции
y=cosx
, нарисуем её график.
1. Область определения — все действительные числа (множество
ℝ
).
2. Множество значений — промежуток
−1;1
.
3. Функция
y=cosx
имеет период
2π
.
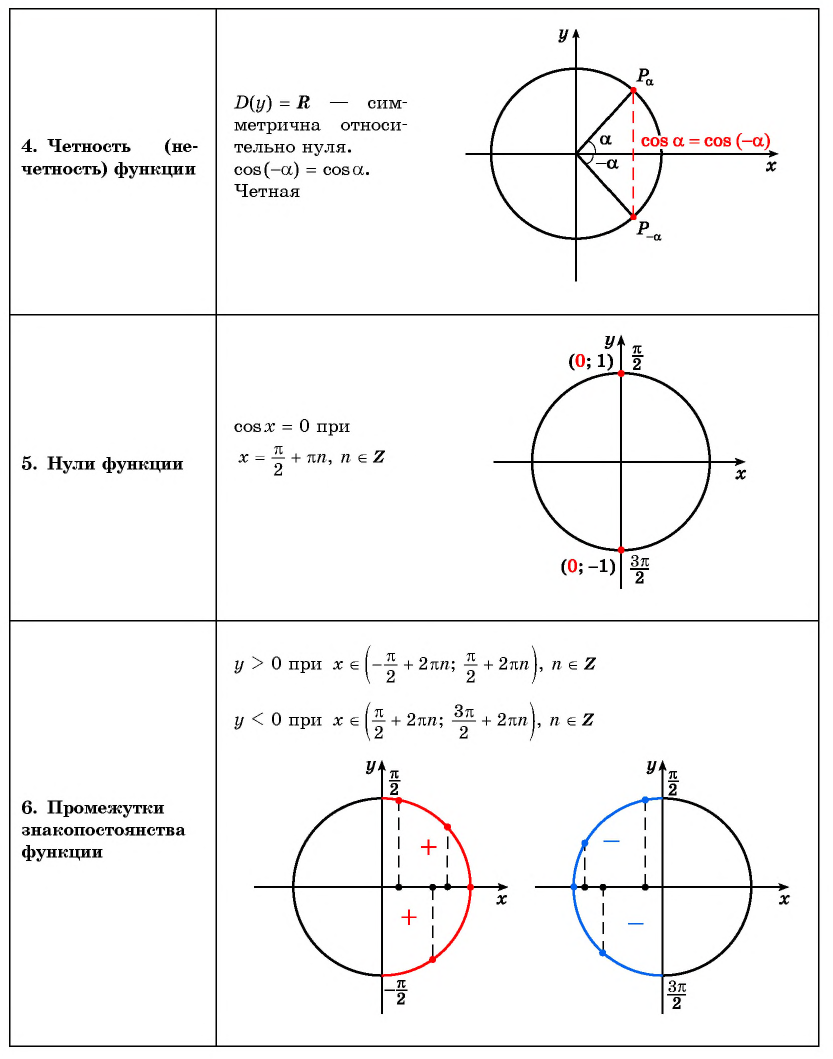
4. Функция
y=cosx
является чётной.
5. Нули функции:
x=π2+πn,n∈ℤ;
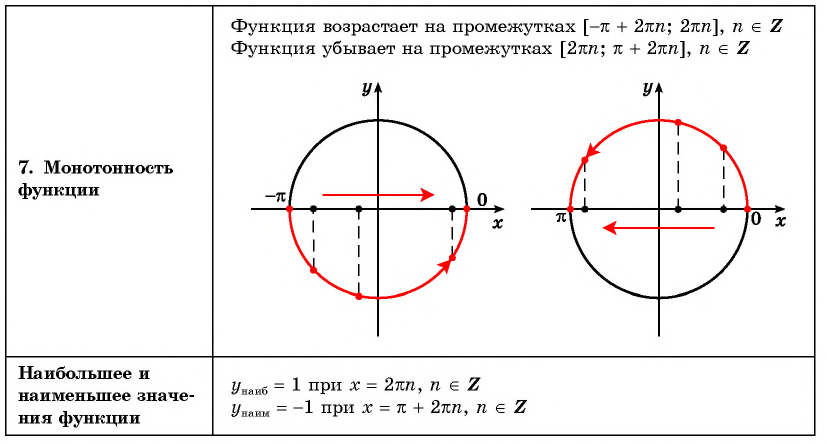
наибольшее значение равно (1) при
x=2πn,n∈ℤ
;
наименьшее значение равно (-1) при
x=π+2πn,n∈ℤ
;
значения функции положительны на интервале
−π2;π2
, с учётом периодичности функции на интервалах
−π2+2πn;π2+2πn,n∈ℤ
;
значения функции отрицательны на интервале
π2;3π2
, с учётом периодичности функции на интервалах
π2+2πn;3π2+2πn,n∈ℤ
.
— возрастает на отрезке
π;2π
, с учётом периодичности функции на отрезках
π+2πn;2π+2πn,n∈ℤ
;
— убывает на отрезке
0;π
, с учётом периодичности функции на отрезках
2πn;π+2πn,n∈ℤ
.
Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Некоторые свойства функции
Например, областью определения функции 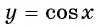
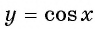
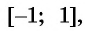
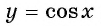
Определение функции y=cos x
Определение:
Зависимость, при которой каждому действительному числу 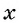
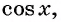
Свойства функции y=cos x
Свойства функции 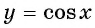
График функции y=cos x
График функции 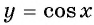
Пример №1
Определите, какие из данных точек принадлежат графику функции
Решение:
а) Подставим в формулу 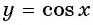
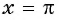
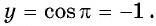
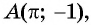
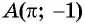
б) При 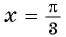
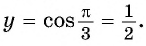
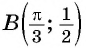
в) При 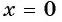
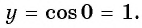
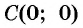
г) При 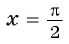
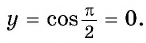
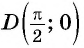
Пример №2
Найдите область определения и множество значений функции
Решение:
Областью определения функции является множество всех действительных чисел, т. е.
Множеством значений функции 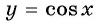
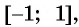
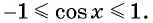
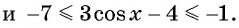
Пример №3
Найдите наименьшее значение функции
Решение:
Так как 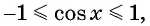
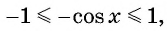
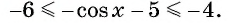
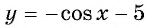
Пример №4
Используя свойство периодичности функции 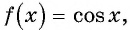
Решение:
Так как число 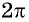
- Заказать решение задач по высшей математике
Пример №5
Используя свойство четности функции 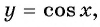
Решение:
Так как функция 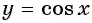
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
а) 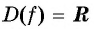
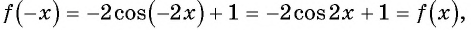
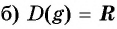
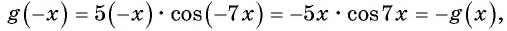
Пример №7
Найдите нули функции:
Решение:
а) Пусть 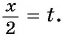
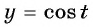
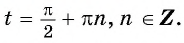
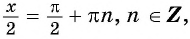
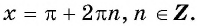
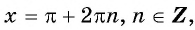
б) Пусть 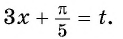
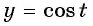
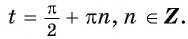
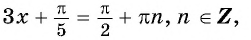
Таким образом, числа 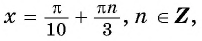
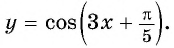
Пример №8
Определите знак произведения
Решение:
Так как 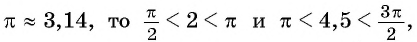
4,5 радиана и 2 радиана принадлежат промежутку 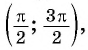
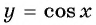
Угол 7 радиан принадлежит промежутку, на котором функция 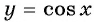
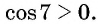
Пример №9
Что больше:
Решение:
Так как функция 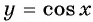
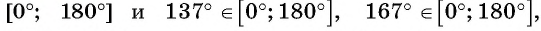
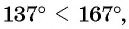
Пример №10
Постройте график функции:
Решение:
а) График функции 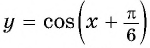
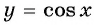
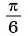
б) График функции 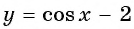
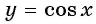
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Развертка абсциссы движения точки по числовой окружности в функцию от угла
- Свойства функции y=cosx
- Примеры
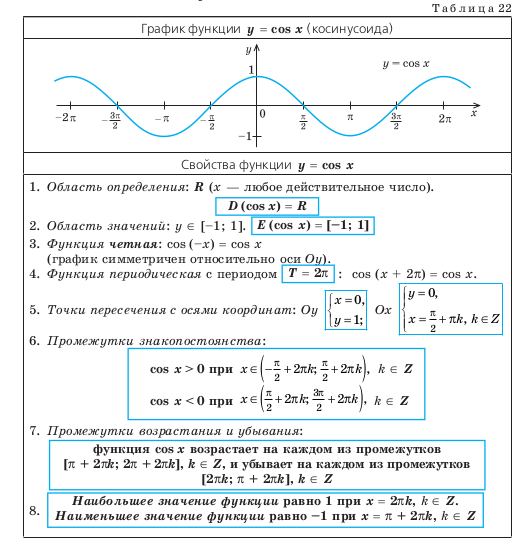
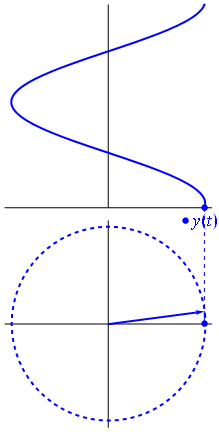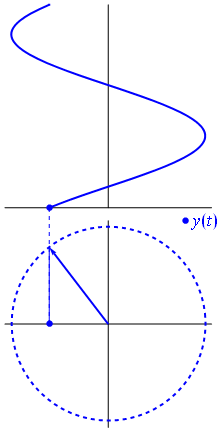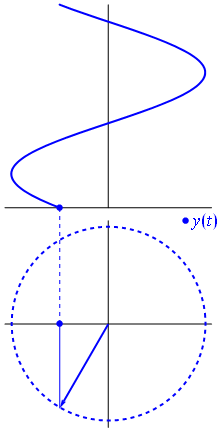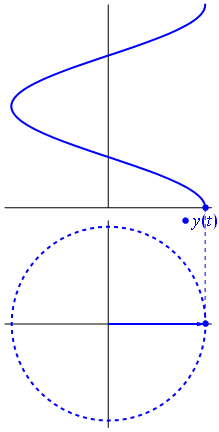
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
Развертка абсциссы движения точки по числовой окружности в функцию от угла (см. §2 данного справочника).
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=cosx для любого (xinmathbb{R}).
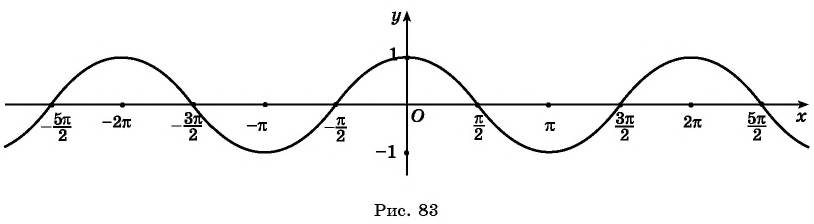
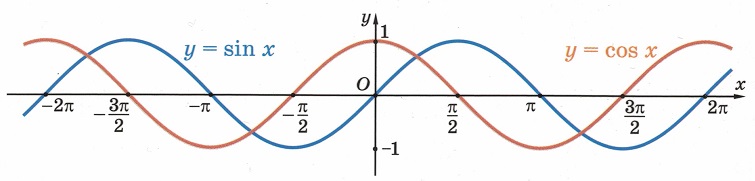
График y=cosx называют косинусоидой.
Часть косинусоиды для –π≤x≤π называют волной косинусоиды.
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды.
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции y=cosx
1. Область определения (xinmathbb{R}) — множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$
5. Максимальные значения (y_{max}=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_{min}=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_{0}=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)
6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=cosleft(frac{3pi}{4}right)=-frac{sqrt{2}}{2}, y_{max}=cosleft(fracpi6right)=frac{sqrt{3}}{2} $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=cos(pi)=-1, y_{max}=cosleft(frac{5pi}{3}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)
Один корень: (x=fracpi2)
б) (cosx-x=1)
(cosx=x+1)
Один корень: x = 0
в) (cosx-x^2=1)
(cosx=x^2+1) 
Один корень: x = 0
г*) (cosx-x^2+frac{pi^2}{4}=0)
(cosx=x^2-frac{pi^2}{4})
(y=x^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_{1,2}=pmfracpi2)
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$ 
(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) — исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) — период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac{x}{2}) — период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).
14. Свойства функций синуса, косинуса, тангенса
и котангенса и их графики
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
Т а б л и ц а 21
|
График функции y = sin x (синусоида) |
 |
|
Свойства функции y = sin x |
 |
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:
1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями
координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее
значения функции.
З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох
(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордина-
та соответствующей точки единичной окружности
(рис. 79). Поскольку ординату можно найти для
любой точки единичной окружности (в силу того,
что через любую точку окружности всегда можно
провести единственную прямую, перпендикуляр-
ную оси ординат), то область определения функции
y = sin x — все действительные числа. Это можно за-
писать так: D (sin x) = R.
Для точек единичной окружности ординаты нахо-
дятся в промежутке [–1; 1] и принимают все значения
от –1 до 1, поскольку через любую точку отрезка [–1; 1]
Рис. 79
оси ординат (который является диаметром единичной
окружности) всегда можно провести прямую, перпендикулярную оси орди-
нат, и получить точку окружности, которая имеет рассматриваемую орди-
нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].
Это можно записать так: E (sin x) = [–1; 1].
Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции sin x равно минус единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть
при
Как было показано в § 13, синус — нечетная функция: sin(-x)= — sin x,
поэтому ее график симметричен относительно начала координат.
В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом
T = 2π: sin (x + 2π) = sin x, таким образом, через промежутки длиной 2π вид графика функции sin x повторя-
ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной 2π, а
потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние kT = 2πk, где
k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых sin x, то есть ордината соответствующей точки единичной окруж
ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-
ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции синус положительны (то есть ордината соответствующей точки
единичной окружности положительна) в I и II четвертях (рис. 80). Таким
образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех
x ∈ (2πk; π + 2πk), k ∈ Z.
Значения функции синус отрицательны (то есть ордината соответствую-
щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-
му sin x < 0 при x ∈ (π + 2πk; 2π + 2πk), k ∈ Z.
Промежутки возрастания и убывания
Доказательство теоремы
Учитывая периодичность функции sin x с периодом T = 2π, достаточно
исследовать ее на возрастание и убывание на любом промежутке длиной
2π, например на промежутке
то при увеличении аргумента x (x2> x1) ордината соответствующей точки единичной окружности увеличивается (то есть
sin x 2 > sin x 1 ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,
делаем вывод, что она также возрастает на каждом из промежутков
Если x ∈ 
окружности уменьшается (то есть sin x 2 < sin x 1 ), таким образом, на этом промежутке функция sin x убывает. Учитывая
периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой
функции (с периодом 2π), достаточно сначала построить график на любом промежутке длиной 2π, например на
промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината
соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на
промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для
построения графика на промежутке [–π; 0] отображаем полученную кривую симметрично относительно начала координат
(рис. 83).
Поскольку мы построили график на
промежутке длиной 2π, то, учитывая
периодичность синуса (с периодом 2π),
повторяем вид графика на каждом про-
межутке длиной 2π (то есть переносим па-
раллельно график вдоль оси Ох на 2πk,
где k — целое число).
Получаем график, который называется
синусоидой (рис. 84).
З а м е ч а н и е. Тригонометрические функции широко применяются в математике, физике и технике. Например,
множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,
описываются функцией, которая задается формулой y = A sin (ωх + φ). Такие процессы называют гармоническими
колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль
координатных осей и параллельным переносом вдоль оси Ох. Чаще всего гармоническое колебание является функцией
времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная
фаза,
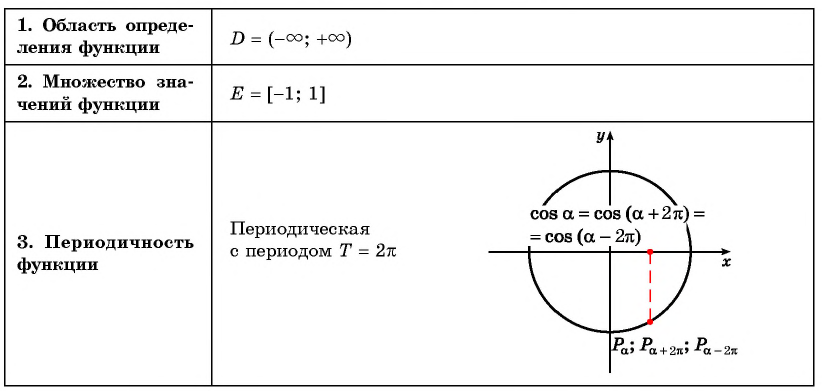
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Объяснение и обоснование
Напомним, что значение косинуса — это абсцис-
са соответствующей точки единичной окружности
(рис. 85). Поскольку абсциссу можно найти для лю-
бой точки единичной окружности (в силу того, что
через любую точку окружности, всегда можно про-
вести единственную прямую, перпендикулярную оси
абсцисс), то область определения функции y = cos x —
все действительные числа. Это можно записать так:
D (cos x) = R.
Для точек единичной окружности абсциссы нахо-
дятся в промежутке [–1; 1] и принимают все значе-
ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной
окружности)
всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции y = cos x:
y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это
значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка B, то есть при x = π + 2πk, k ∈ Z.
Как было показано в § 13, косинус — четная функция: cos (–x) = cos x, поэтому ее график симметричен относительно оси
Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом
T = 2π: cos (x + 2π) = cos x. Таким образом, через промежутки длиной 2π вид графика функции cos x повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oy значение x = 0. Тогда
соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только
тогда, когда на единичной окружности будут выбраны точки C или D, то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции косинус положительны (то есть абсцисса соответствующей точки
единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-
тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех
Значения функции косинус отрицательны (то есть абсцисса соответству-
ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,
поэтому cos x < 0 при x ∈
Промежутки возрастания и убывания
Учитывая периодичность функции cos x (T = 2π), достаточно исследовать
ее на возрастание и убывание на любом промежутке длиной 2π, например
на промежутке [0; 2π].
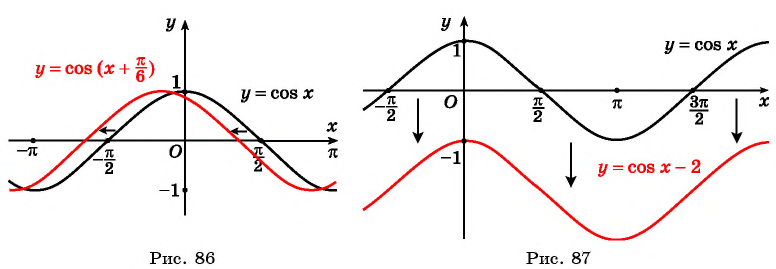
Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x 2 > x 1 ) абсцисса соответствующей точки единичной
окружности уменьшается (то есть cos x 2<cos x 1 ), следовательно, на этом промежутке функция cos x убывает. Учитывая
периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.
Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x 2 > x 1 ) аб-
сцисса соответствующей точки единичной окружности увеличивается (то
есть cos x 2 >cos x 1 ), таким образом, на этом промежутке функция cos x
возрастает. Учитывая периодичность функции cos x, делаем вывод, что
она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.
Проведенное исследование позволяет построить график функции y = cos x
аналогично тому, как был построен график функ-
ции y = sin x. Но график функции у = cos x можно
также получить с помощью геометрических преоб-
разований графика функции у = sin х, используя
формулу
Эту формулу можно обосновать, например, так.
Рассмотрим единичную окружность (рис. 88), отметим на ней точки

Таблицы DPVA.ru — Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru: 
|
|||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator