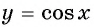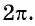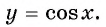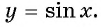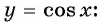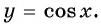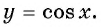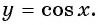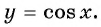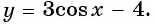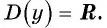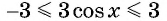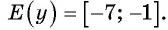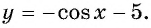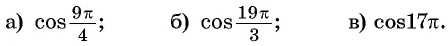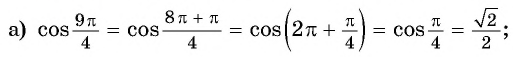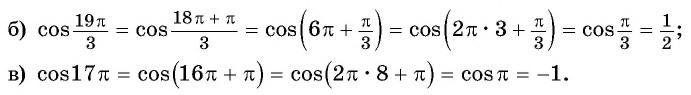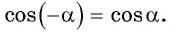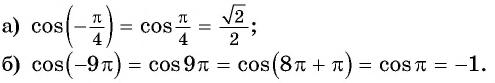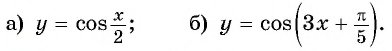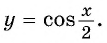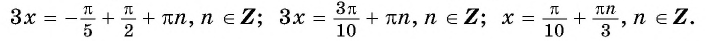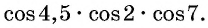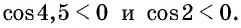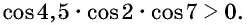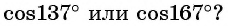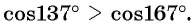Функция
y=cosx
определена на всей числовой прямой, и множеством её значений является отрезок
−1;1
.
Поэтому её график не выходит за границы полосы между прямыми
y=−1
и
y=1
.
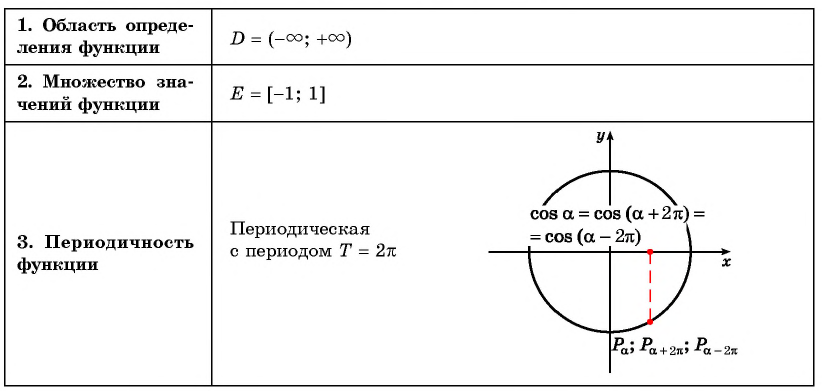
Используя свойство периодичности функции
y=cosx
, можно построить её график на промежутке
−π≤x≤π
длиной
2π
и повторить несколько периодов с такими же значениями.
Функция
y=cosx
— чётная. Её график симметричен относительно оси (Oy).
Построим график функции на промежутке
−π≤x≤π
. Так как функция
y=cosx
является чётной, можно построить график на промежутке
0≤x≤π
, а потом симметрично отобразить относительно оси (Oy).
Значения функции в удобных точках на этом отрезке
0≤x≤π
равны:
cos0=1;cosπ6=32;cosπ4=22;cosπ3=12;cosπ2=0;cosπ=−1
.
Учитывая периодичность функции
y=cosx
, нарисуем её график.
1. Область определения — все действительные числа (множество
ℝ
).
2. Множество значений — промежуток
−1;1
.
3. Функция
y=cosx
имеет период
2π
.
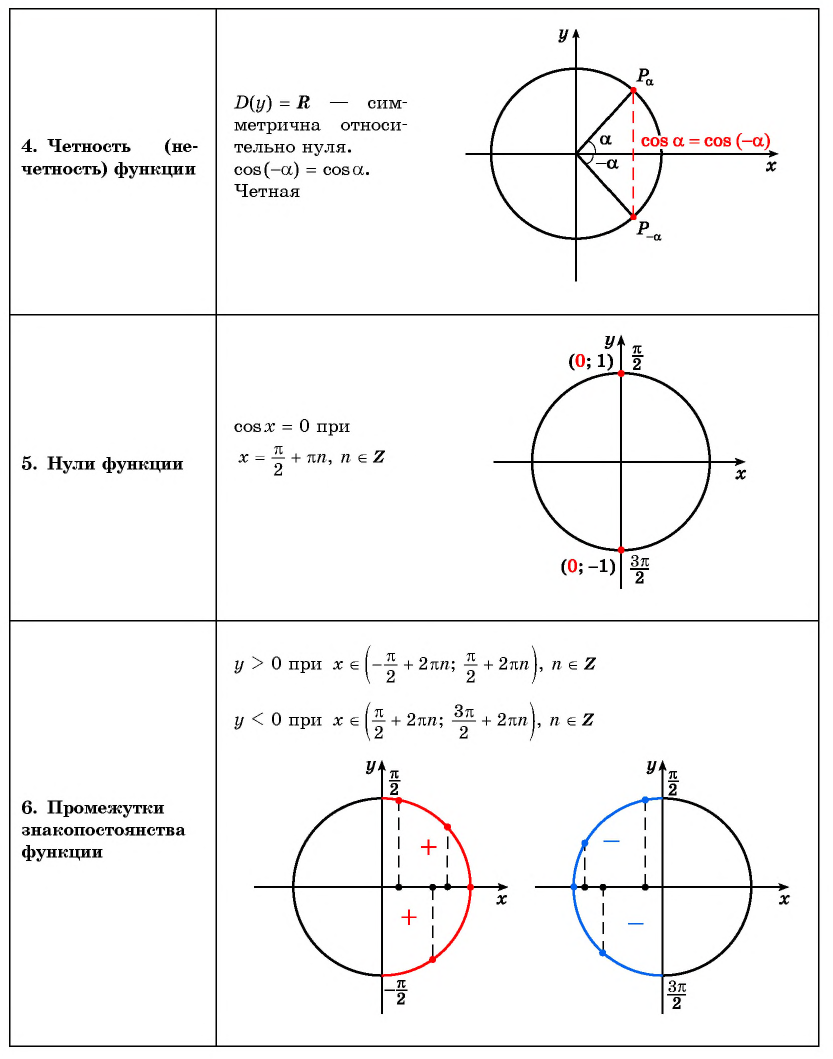
4. Функция
y=cosx
является чётной.
5. Нули функции:
x=π2+πn,n∈ℤ;
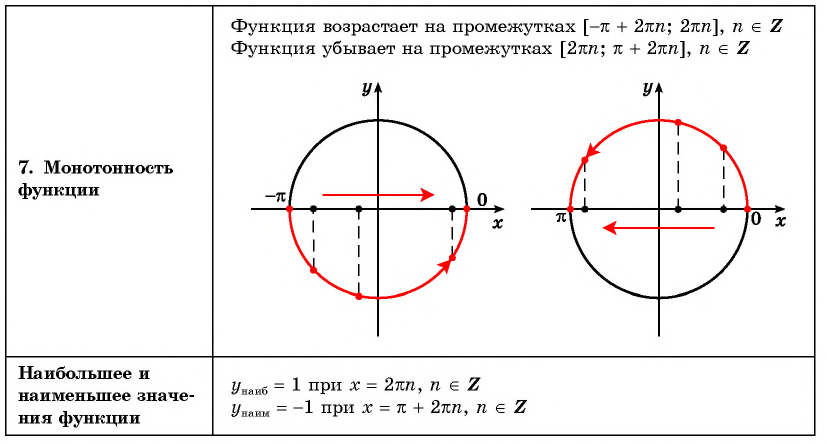
наибольшее значение равно (1) при
x=2πn,n∈ℤ
;
наименьшее значение равно (-1) при
x=π+2πn,n∈ℤ
;
значения функции положительны на интервале
−π2;π2
, с учётом периодичности функции на интервалах
−π2+2πn;π2+2πn,n∈ℤ
;
значения функции отрицательны на интервале
π2;3π2
, с учётом периодичности функции на интервалах
π2+2πn;3π2+2πn,n∈ℤ
.
— возрастает на отрезке
π;2π
, с учётом периодичности функции на отрезках
π+2πn;2π+2πn,n∈ℤ
;
— убывает на отрезке
0;π
, с учётом периодичности функции на отрезках
2πn;π+2πn,n∈ℤ
.
Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Некоторые свойства функции
Например, областью определения функции 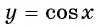
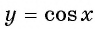
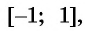
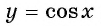
Определение функции y=cos x
Определение:
Зависимость, при которой каждому действительному числу 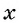
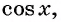
Свойства функции y=cos x
Свойства функции 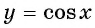
График функции y=cos x
График функции 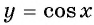
Пример №1
Определите, какие из данных точек принадлежат графику функции
Решение:
а) Подставим в формулу 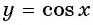
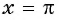
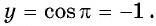
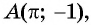
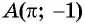
б) При 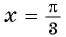
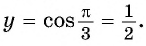
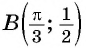
в) При 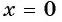
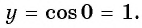
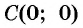
г) При 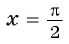
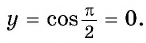
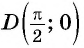
Пример №2
Найдите область определения и множество значений функции
Решение:
Областью определения функции является множество всех действительных чисел, т. е.
Множеством значений функции 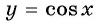
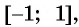
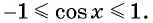
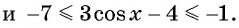
Пример №3
Найдите наименьшее значение функции
Решение:
Так как 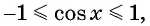
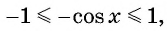
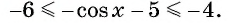
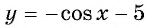
Пример №4
Используя свойство периодичности функции 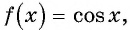
Решение:
Так как число 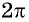
- Заказать решение задач по высшей математике
Пример №5
Используя свойство четности функции 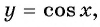
Решение:
Так как функция 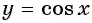
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
а) 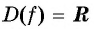
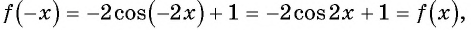
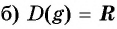
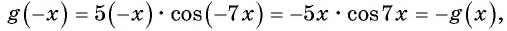
Пример №7
Найдите нули функции:
Решение:
а) Пусть 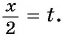
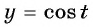
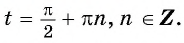
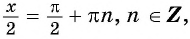
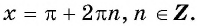
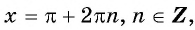
б) Пусть 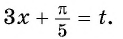
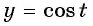
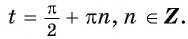
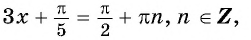
Таким образом, числа 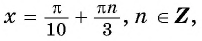
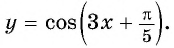
Пример №8
Определите знак произведения
Решение:
Так как 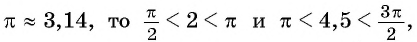
4,5 радиана и 2 радиана принадлежат промежутку 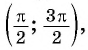
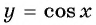
Угол 7 радиан принадлежит промежутку, на котором функция 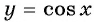
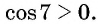
Пример №9
Что больше:
Решение:
Так как функция 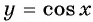
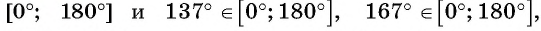
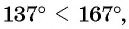
Пример №10
Постройте график функции:
Решение:
а) График функции 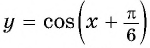
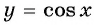
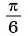
б) График функции 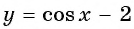
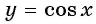
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
Определения
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
Косинус угла А обозначается cos A.
Наглядно это видно на следующем рисунке:
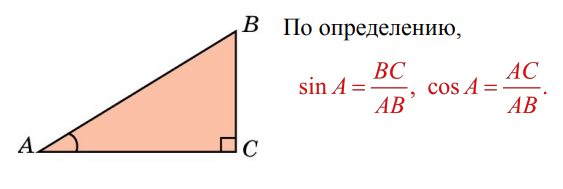
Функция косинуса: свойства и значения функции косинус
Определение
Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.
- Основные свойства функции косинус следующие:
- Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
- Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
- Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
- Функция чётная, т. е. cos(-x) = cos(x);
- Функция периодическая. Её период равен 2π;
- Наибольшего своего значения функция косинус x достигает в точках x=2πk;
- Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
- Область возрастания функции cos(x): -π+2πk<=x<=2πk;
- Область убывания функции cos(x): 2πk<= π+2πk;
- Функция не имеет разрывов, т. е. непрерывна.
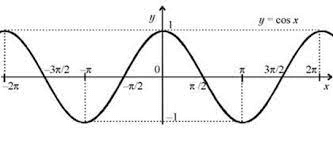
График функции косинус
Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние [frac{pi}{2}] влево. Он выглядит следующим образом:
Как построить график функции косинус икс
График функции косинуса можно построить следующим образом:
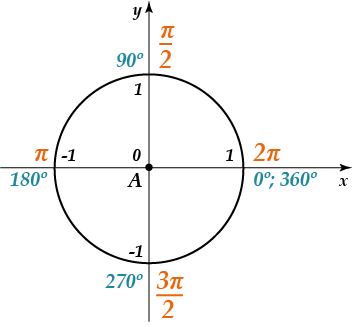
Используем данные единичной окружности, приведённой на рисунке выше.
Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.
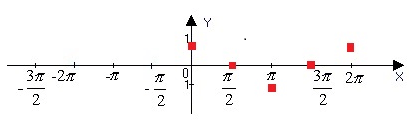
Соединим их плавной линией
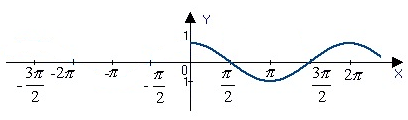
Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.
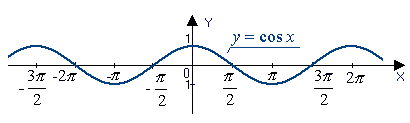
Нет времени решать самому?
Наши эксперты помогут!
Как найти значение функции косинуса при x равном 45 градусам
Построим прямоугольный треугольник с катетами, равняющимися единице. Сумма углов любого треугольника, как известно, равна 180 градусам. Если вычтем из них прямой угол, получим сумму двух оставшихся углов. Это углы при вершинах A и B. Так как катеты равны, то и выше названные углы равны и каждый из них составляет (180 – 90)/2 = 45 градусов.
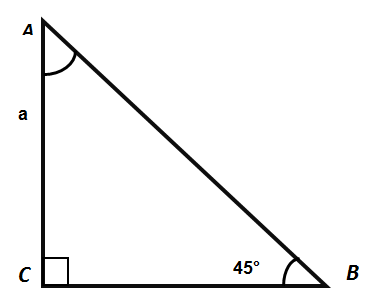
По теореме Пифагора гипотенуза его в этом случае будет равна [c=sqrt{a^{2}+a^{2}}=sqrt{1+1}=sqrt{2}]
Из определения косинуса находим [cos (a)=1 / sqrt{2}]
После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.
Как найти нули тригонометрической функции по уравнению
Ключевые слова: тригонометрия, функция, синус, косинус, тангенс, котангенс, область определения, множество значений
D(tg) = R, $$x ne frac<pi><2>+pi n$$
Нули функции
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
1) Найти нули линейной функции y=3x+15.
Чтобы найти нули функции, решим уравнение 3x+15 =0.
Таким образом, нуль функции y=3x+15 — x= -5 .
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Для нахождения нулей функции решим квадратное уравнение
Его корни x1=3 и x2=4 являются нулями данной функции.
3)Найти нули функции
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
| Свойства | y = sin x |
y = cos x | y = tg x | y = ctg x | |||
| D(f) — область определения функции | D(sin) = R — множество всех действительных чисел | D(cos) = R — множество всех действительных чисел | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| sin α | 0 | 1 2 | 2 2 | 3 2 | 1 | ||
| cos α | 1 | 3 2 | 2 2 | 1 2 | 0 | ||
| tg α | 0 | 3 3 | 1 | 3 | нет | ||
| ctg α | нет | 3 | 1 | 3 3 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
- Развертка абсциссы движения точки по числовой окружности в функцию от угла
- Свойства функции y=cosx
- Примеры
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
Развертка абсциссы движения точки по числовой окружности в функцию от угла (см. §2 данного справочника).
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
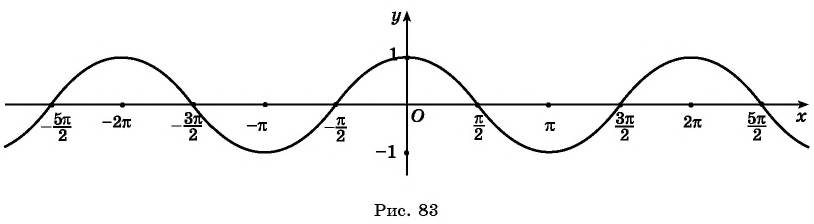
В результате получаем график y=cosx для любого (xinmathbb{R}).
График y=cosx называют косинусоидой.
Часть косинусоиды для –π≤x≤π называют волной косинусоиды.
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды.
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции y=cosx
1. Область определения (xinmathbb{R}) — множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$
5. Максимальные значения (y_{max}=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_{min}=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_{0}=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)
6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=cosleft(frac{3pi}{4}right)=-frac{sqrt{2}}{2}, y_{max}=cosleft(fracpi6right)=frac{sqrt{3}}{2} $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=cos(pi)=-1, y_{max}=cosleft(frac{5pi}{3}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)
Один корень: (x=fracpi2)
б) (cosx-x=1)
(cosx=x+1)
Один корень: x = 0
в) (cosx-x^2=1)
(cosx=x^2+1) 
Один корень: x = 0
г*) (cosx-x^2+frac{pi^2}{4}=0)
(cosx=x^2-frac{pi^2}{4})
(y=x^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_{1,2}=pmfracpi2)
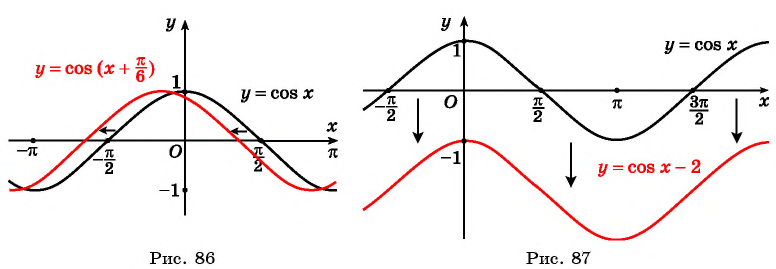
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$ 
(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) — исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) — период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac{x}{2}) — период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).