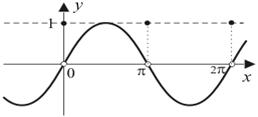
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Определение
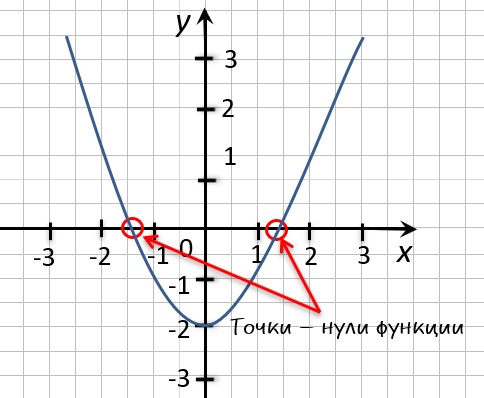
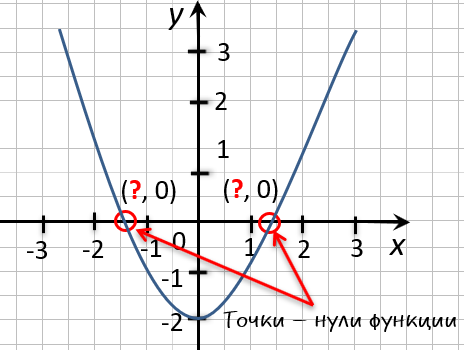
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!
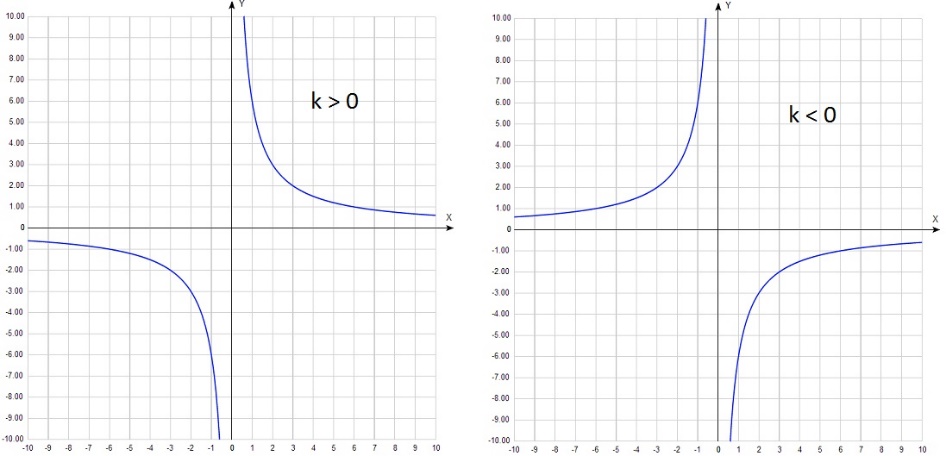
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом:
По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции.
Пример №1. Найти нули функции (если они существуют):
а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Даниил Романович | Просмотров: 16.1k
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом: 
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
- а) у= –11х +22
- б) у= (х + 76)(х – 95)
- в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
- Находим х, разделив 22 на 11: х=22:11
- Получим х=2.
- Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0.
Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95.
Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Метод интервалов: примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x) или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
произведение линейных двучленов с коэффициентом 1 при переменной х;
произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
- (x+3)·(x2−x+1)·(x+2)3≥0,
- (x-2)·(x+5)x+3>0 ,
- (x−5)·(x+5)≤0,
- (x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≥, то выделяем штриховкой участки, отмеченные знаком «+».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t
-
Нули функции и промежутки знакопостоянства
Нулем
функцииназывается такое значение
ее аргумента, при котором значение
функции равно нулю:.
Множество нулей функции
–
это следующее множество:
.
Промежутком
знакопостоянства функции
называется промежуток значений ее
аргумента, входящий в ООФ,
во всех точках которого функция принимает
значения одного знака: или
.
Множества промежутков знакопостоянства
функции
обозначаются следующим образом:
,
.
Пример
2 (нули
и промежутки знакопостоянства функции)
Найти
множества нулей и промежутков
знакопостоянства заданных функций:
1)
2)
Решение
1)
ООФ:
;
данная функция имеет два нуля, которые
разбивают ее ООФ на промежутки
знакопостоянства функции:
знак функции на каждом из обозначенных
промежутков можно определить по
точке-представительнице промежутка,
если вычислить знак значения функции
в этой точке:
при
;
при
;
при
;
при
;
Т
образом, получено, чтопри
или
;
при
;
при
;
Нули функции и промежутки ее знакопостоянства
вместе с ООФдают первичную информацию
о расположении графика функции на
координатной плоскости
:
|
точки
прямая график будет расположен
выше оси
ниже оси |
|
2)
ООФ:
;
,
следовательно, функция имеет два нуля;
промежутки знакопостоянства функции:
при
илиx= 1;
при
;
при
.
Ответ:
1)
2)
-
Четность, нечетность функций
Функцияназываетсячетной
функцией, если выполняются
следующие два условия:
График четной функции всегда имеет
осевую симметрию относительно оси
функции (рис.45).
Функция
называетсянечетной функцией,
если выполняются следующие два условия:
График нечетной функции всегда имеет
центральную симметрию относительно
начала координат (рис.46).
Рис.45
Рис.46
Пример
3 (исследование
функций на четность)
Исследовать
следующие функции на четность:
1)
;
2)
;
3)
;
4)
.
Решение
1)
;
ООФсимметрична относительно точкиx = 0;
вычисляем
,
используя четность основных элементарных
функций
и
:
;
равенство
выполняется для
,
поэтому данная функция является четной,
ее график будет симметричным относительно
осиOY;
2)
ООФявляется симметричной относительно
точкиx = 0;
вычисляем
,
учитывая, что
,
:
равенство
выполняется при
,
поэтому данная функция является нечетной
и ее график будет иметь центральную
симметрию относительно начала координат;
3)
– есть симметрияООФотносительно
точкиx = 0;
вычисляем
:
здесь не выполняется ни одно из равенств
или
,
поэтому данная функция не является ни
четной, ни нечетной, следовательно,
симметрию её графика предсказать нельзя;
4)
ООФне является симметричной
относительно точкиx
= 0, поэтому свойством четности или
нечетности эта функция обладать не
может. Следовательно, она относится к
функциям общего вида, которые не являются
ни четными, ни нечетными.
Ответ:1) функцияявляется четной;
2) функция
является нечетной;
3) функция
не является ни четной, ни нечетной;
4) функция
не
является ни четной, ни нечетной.
-
Периодичность функции
Функцияназываетсяпериодической
функцией, если существует
число
,
такое что верно равенство
График периодической функции имеет
повторяющиеся участки на каждом
промежутке длинойT.
Наименьшее из чиселTназываетсянаименьшим
периодом функции. По
умолчанию буквойТобозначают именно
наименьший период (рис.47).
Рис.47
Исследование периодической функции и
построение ее графика следует проводить
на промежутке, длина которого равна
наименьшему периоду функции; этот
промежуток часто называютосновным
промежутком для периодической функции.
Ниже перечислены некоторые свойства
периодических функций:
-
Периодическая функция не может быть
задана на множестве, ограниченном
сверху или ограниченном снизу.
Например, функция,
не является периодической.
-
Если число
является периодом функции
,
то число,
где,
также является ее периодом.
Например, функция,
является периодической, её наименьший
периоди
числа,
также являются ее периодами.
-
Если число
– это наименьший период функции
,
то функцияявляется также периодической и ее
наименьший период равен числу.
Например, функция,
является периодической и ее наименьший
период равен.
-
При сложении двух периодических функций
с одинаковыми ООФ получается
периодическая функция, причем ее
наименьший период делится нацело на
и на
,
где
,
– это наименьшие периоды слагаемых.
Например,
–
периодическая с,
– периодическая с
– периодическая с
,
так каки
.
Примеры
4 (определение
периодичности функций)
1.
Является ли функция периодической?
Чему равен ее наименьший период?
Решение
Известно, что основная элементарная
функцияявляется периодической с наименьшим
периодом
.
Проверим равенство
для данной функции:
По выполнению равенства заключаем, что
данная функция является периодической
с периодом
.
Чтобы найти наименьший период, понизим
степень выражения
по известной тригонометрической формуле:
.
Тогда
.
Теперь имеем сумму двух периодических
функций:
,
,
,
периодом является любое положительное
число;
следовательно, данная функция
имеет наименьший период
;
поэтому исследовать ее свойства и
строить график достаточно на основном
промежутке, например при
,
а затем сделать периодическое продолжение
на всюООФ.
Ответ:функция
является периодической с наименьшим
периодом.
2.
Является ли функция периодической?
Решение
Данная сложная функция не является
периодической, так как не является
периодической её промежуточная функция,
«искажающая» те значения аргументаx, для которых одинаковые
значения имела бы функция.
Для иллюстрации сказанного проверим
расположение нулей данной функции:
Имеем
множество всех нулей функции:
Видим, что нули функции располагаются
непериодически на оси OX.
Следовательно, данная функция не является
периодической (так как в противном
случае все её свойства, в том числе и
нули, повторялись бы периодически).
Ответ:
функцияне является периодической.
3.Укажите, какие из следующих функций
являются периодическими?
1)
;
2)
;
3)
; 4)
.
Решение
-
Функция
периодической не является, так как
равенство
не выполняется, например, для точки
,
потому что точкаиз-за ограниченности снизуООФ(рис.48);
2) функция периодической не является,
так как равенство
не выполняется, например, для точки
(рис.49);
Рис.48
Рис.49
3) функция является периодической с
наименьшим периодом
,
что хорошо видно по ее графику на рис.
50;
4) функция является периодической с
наименьшим периодом
,
что хорошо видно по ее графику на рис.
51;
Рис.
50 Рис.51
Ответ:периодическими являются только функции
3) и 4).
Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
Разбор примера
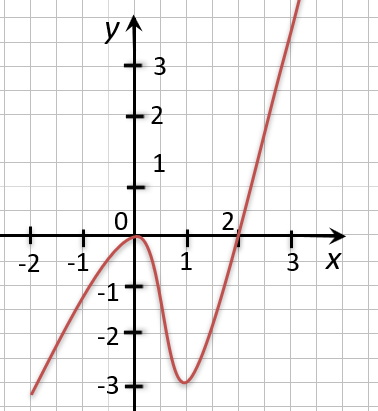
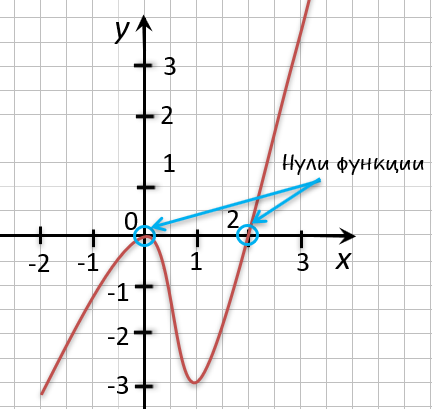
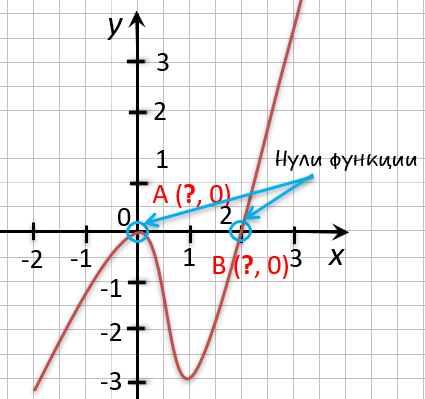
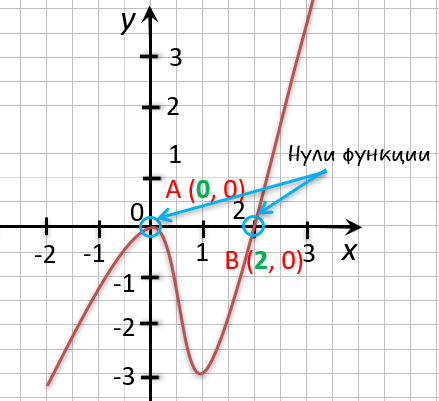
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
На
прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились
находить область определения и область значений функции.
Свойства
функций:
·
нули
функции;
·
промежутки
знакопостоянства функции;
·
промежутки
монотонности функции.
Нули
функции
Определение:
Нулями
функции называют такие значения аргумента, при которых
функция равна нулю.
В
данном случае функция задана графически и мы
определили нули функции по графику. Так же нули функции можно находить по
формуле, с помощью которой задана функция.
Решив
уравнение, мы найдём те значения х, при которых функция равна нулю.
Стоит
обратить внимание на то, что не каждая функция имеет нули.
График
не пересекает ось икс ни в одной точке.
Промежутки
знакопостоянства функции
Определение:
Промежутки
знакопостоянства функции
— это такие промежутки из области определения, на которых данная функция
принимает значения только одного знака, либо положительные, либо отрицательные.
Функция
принимает положительные значения:
И
отрицательные значения:
Запишите
промежутки знакопостоянства функции:
Положительные
и отрицательные значения функции:
Промежутки
монотонности функции
Определение:
Функция
называется возрастающей в некотором промежутке, если большему значению
аргумента из этого промежутка соответствует большее значение функции.
Определение:
Функция
называется убывающей в некотором промежутке, если большему значению
аргумента из этого промежутка соответствует меньшее значение функции.
Определение:
Промежутками
монотонности называют такие промежутки из области
определения, на которых функция либо возрастает, либо убывает.
Опишем
свойства функции:
Графиком
является прямая, поэтому для построения достаточно
двух точек:
Найдём
значения функции:
Областью
определения и областью значений будет множество всех действительных чисел. Ведь
х и у могут быть любыми числами.
Найдём
нули функции:
Запишем
промежутки знакопостоянства:
Запишем
промежутки монотонности: