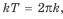Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 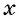
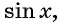
Рассмотрим свойства функции 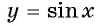
Область определения функции y=sin x
Областью определения функции 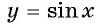
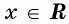
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 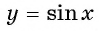
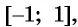
Графически это означает, что график функции 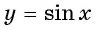
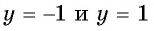
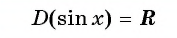
Периодичность функции y=sin x
Периодичность функции 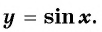
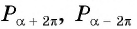
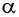
Говорят, что число 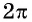
Определение:
Функция 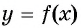
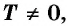
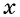
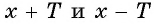
Чтобы определить, является ли функция периодической с периодом 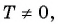
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 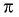
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 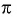
Периодом функции 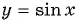
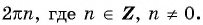
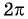
Функция 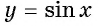
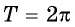
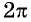
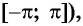
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 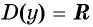
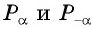
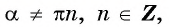
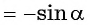
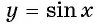
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек 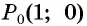
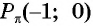
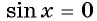
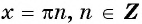
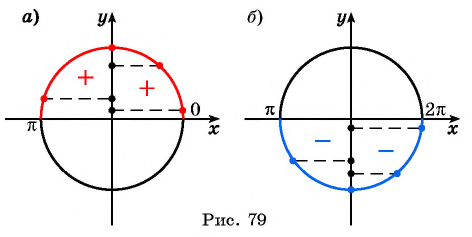
Промежутки знакопостоянства функции y=sin x
На промежутках 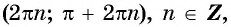
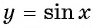
На промежутках 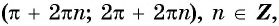
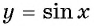
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 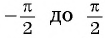
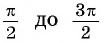
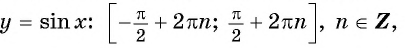
Функции 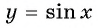
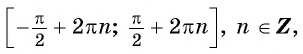
Наибольшее значение функции 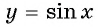
Наименьшее значение функции 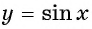
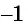
На основании проведенного исследования построим график функции 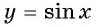
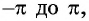
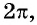
На этом периоде функция
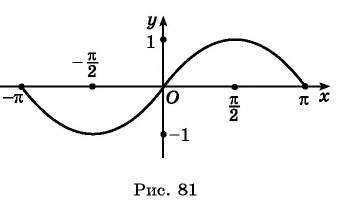
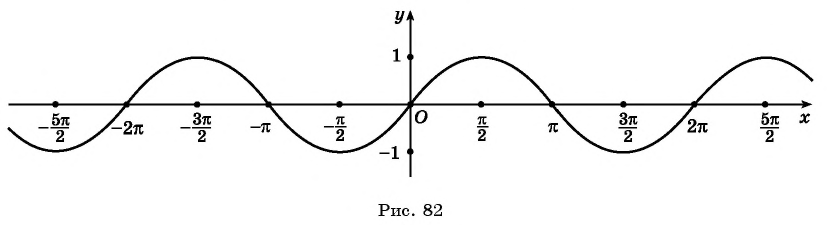
На рисунке 81 изображена часть графика функции 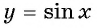
Перенесем эту часть на другие периоды и получим график функции 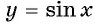
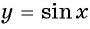
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 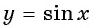
Решение:
а) Подставим в формулу 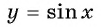
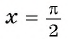
Полученное значение функции равно ординате точки 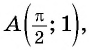
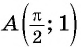
б) При 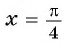
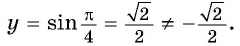
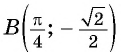
в) При 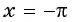
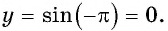
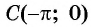
г) При 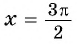
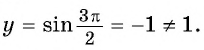
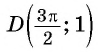
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 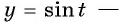
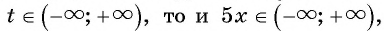
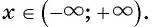
Множеством значений функции 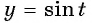
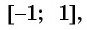
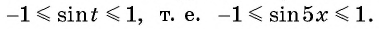
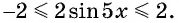
б) 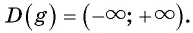
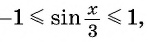
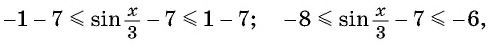
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 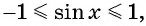
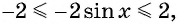
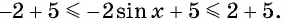
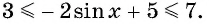
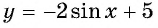
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 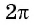
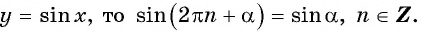
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 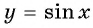
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
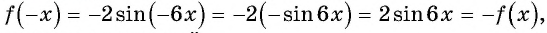
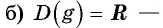
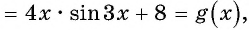
Пример №7
Найдите нули функции:
Решение:
а) Пусть 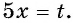
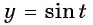
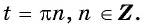
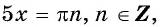
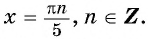
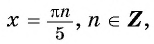
б) Пусть 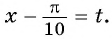
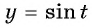
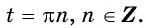
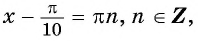
Таким образом, числа 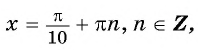
Пример №8
Определите знак произведения
Решение:
Так как 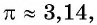
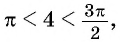
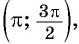
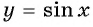
Углы 2 радиана и 1 радиан принадлежат промежутку 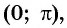
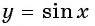
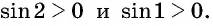
Пример №9
Что больше: 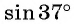
Решение. Так как функция 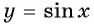
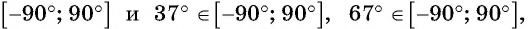
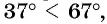
Пример №10
Постройте график функции:
Решение:
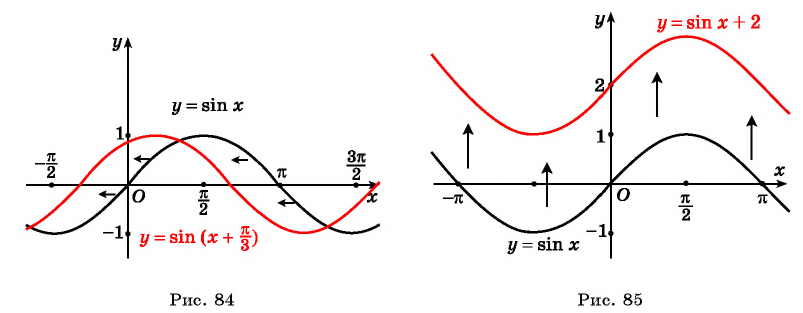
а) График функции 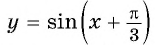
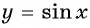
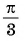
б) График функции 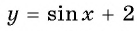
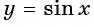
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
Область определения: (D(x)=R).
(y(-x)=-y(x)) — нечётная.
Построение графика этой функции происходит таким же способом, как и графика функции
y=cosx
, начиная с построения, например, на отрезке
0;π
.
Но можно упростить, применив формулу
sinx=cosx−π2
, которая показывает, что график функции
y=sinx
можно получить путём сдвига графика функции
y=cosx
вдоль оси абсцисс вправо на
π2
.
Кривая, являющаяся графиком функции
y=sinx
, называется синусоидой.
1. Область определения — множество
ℝ
всех действительных чисел.
2. Множество значений — отрезок
−1;1
.
3. Функция
y=sinx
имеет период (T =)
2π
.
4. Функция
y=sinx
является нечётной.
5. Нули функции:
x=πn,n∈ℤ
;
наибольшее значение равно (1) при
x=π2+2πn,n∈ℤ
;
наименьшее значение равно (-1) при
x=−π2+2πn,n∈ℤ
;
значения функции положительны на интервале
0;π
, с учётом периодичности функции на интервалах
2πn;π+2πn,n∈ℤ
;
значения функции отрицательны на интервале
π;2π
, с учётом периодичности функции на интервалах
π+2πn;2π+2πn,n∈ℤ
.
— возрастает на отрезках
−π2;π2
, с учётом периодичности функции на отрезках
−π2+2πn;π2+2πn,n∈ℤ
;
— убывает на отрезке
π2;3π2
, с учётом периодичности функции на отрезках
π2+2πn;3π2+2πn,n∈ℤ
.
- Развертка ординаты движения точки по числовой окружности в функцию от угла
- Свойства функции y=sinx
- Примеры
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
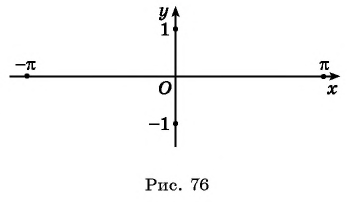
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=sinx для любого (xinmathbb{R}).
График y=sinx называют синусоидой.
Часть синусоиды для 0≤x≤2π называют волной синусоиды.
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды.
п.2. Свойства функции y=sinx
1. Область определения (xinmathbb{R}) — множество действительных чисел.
2. Функция ограничена сверху и снизу
$$ -1leq sinxleq 1 $$
Область значений (yin[-1;1])
3. Функция нечётная
$$ sin(-x)=-sinx $$
4. Функция периодическая с периодом 2π
$$ sin(x+2pi k)=sinx $$
5. Максимальные значения (y_{max}=1) достигаются в точках
$$ x=fracpi2+2pi k $$
Минимальные значения (y_{min}=-1) достигаются в точках
$$ x=-fracpi2+2pi k $$
Нули функции (y_{0}=sinx_0=0) достигаются в точках (x_0=pi k)
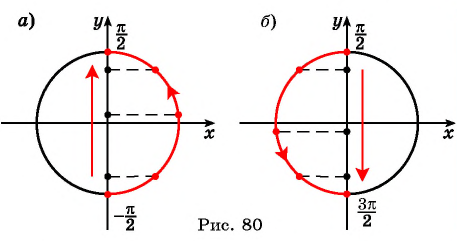
6. Функция возрастает на отрезках
$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$
Функция убывает на отрезках
$$ fracpi2+2pi kleq xleqfrac{3pi}{2}+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=sinleft(fracpi6right)=frac12, y_{max}=sinleft(fracpi2right)=1 $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=sinleft(frac{3pi}{2}right)=-1, y_{max}=sinleft(frac{5pi}{6}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (sinx=3x)
Один корень: x = 0
б) (sinx=2x-2pi)
Один корень: x = π
в) (sinx-sqrt{x-pi}=0)
(sinx=sqrt{x-pi}) 
Один корень: x = π
г*) (sinx=left(x-fracpi2right)^2-frac{pi^2}{4})
(y=left(x-fracpi2right)^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_1=0, x_2=pi)
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$ 
(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) — исходная функция поднимается вверх на 2. Область значений (yin[1;3]).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) — период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac{x}{2}) — период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).
Функция y = sin x – одна из самых распространенных функций в алгебре и математическом анализе. На этом занятии рассмотрим ее свойства и построим график.
Функция y = sin x – это тригонометрическая функция, которая относится к группе основных тригонометрических функций. Она определяется как отношение противолежащего катета и гипотенузы значений прямоугольного треугольника.
Функция sinx – это также функция одной переменной, где аргументом является угол x (в радианах), а значение функции y представляет собой соответствующее значение синуса угла x, выраженного в радианах.
Свойства
Рассмотрим основные свойства функции y = sinx:
- Ограниченность. Функция sinx ограничена сверху и снизу значениями 1 и -1 соответственно. То есть все значения функции находятся в диапазоне от -1 до 1.
- Периодичность. Функция sinx обладает периодичностью, т.е. ее график повторяется через определенные промежутки. Период функции sinx равен 2π, что означает, что значение функции через каждые 2π равняется значению функции в начальной точке.
- Нечетность. Функция sinx является нечетной функцией, т.е. для любого значения x выполняется равенство sin(-x)=-sin(x).
- Максимумы и минимумы. Максимум функции sinx равен 1 и достигается при x=π/2, а минимум функции -1 и достигается при x=3π/2. Промежутки между максимальными/минимальными значениями функции называются амплитудой.
- Нули функции. Нули функции sinx располагаются в точках x=kπ, где k принимает любое целое значение.
- Симметрия. График функции sinx симметричен относительно оси x=π/2, что означает, что при взаимной замене x на π-x функция сохраняется.
- Монотонность. Функция sinx является монотонно возрастающей на интервале от 0 до π/2 и монотонно убывающей на интервале от π/2 до π.
- Дифференцируемость. Функция sinx дифференцируема на всей числовой прямой и ее производная равна функции cosx.
- Интегрируемость. Функция sinx интегрируема на всей числовой прямой. Ее первообразной является функция -cosx.
Построение графика функции
Для построения графика функции y = sin x необходимо точно определить ее значения на некоторых интервалах, а также на разметке осей координат.
- Определение периода функции. Функция y = sin x имеет период 2π, это означает, что график функции повторяется каждые 2π единиц. Для построения графика функции достаточно определить значения функции на интервале от -π до π.
- Определение осей координат. Построить ось абсцисс (ось x) и ось ординат (ось y) перпендикулярно друг к другу и провести через их пересечение начало координат.
- Определение точек пересечения оси x. Функция y = sin x имеет точки пересечения с осью x при x = kπ, где k – целое число. Сложив или вычтя значение π к кратному периода 2π, находим значения x, при которых синус равен 0.
- Определение максимальных и минимальных значений. Максимальное значение функции y = sin x равно 1 и достигается при x = π/2, 5π/2, …, а минимальное значение равно -1 и достигается при x = 3π/2, 7π/2, ….
- Построение на графике точек пересечения с осью x, максимумов и минимумов.
Наносим на график все найденные значения x, при которых функция достигает значения 0.
Они представлены в таблице:
| k | x |
|—|—|
| 0 | 0 |
| 1 | π |
| 2 | 2π |
| 3 | 3π |
На графике отмечаем точки максимума и минимума функции.
- Определение знака функции. Отмечаем на графике интервалы, на которых функция y = sin x положительна, т.е. больше нуля, и интервалы, на которых функция отрицательна, т.е. меньше нуля. Знак синуса меняется при пересечении его периодической оси.
- Построение графика. С помощью табличных значений x и y, с учетом знака функции проводим непрерывную линию через точки и получаем график функции y = sin x.
Поделиться статьей в соцсетях
Остались вопросы?
Наши репетиторы помогут
-
Подготовиться к поступлению в любой ВУЗ страны
-
Подготовится к ЕГЭ, ГИА и другим экзаменам
-
Повысить успеваемость по предметам
Остались вопросы?
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
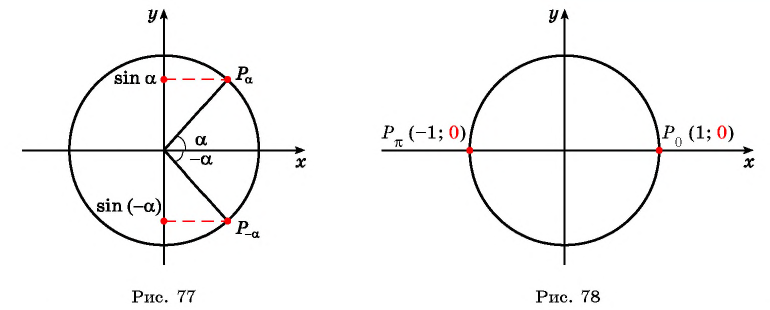
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.

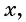
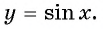
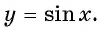
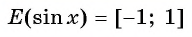
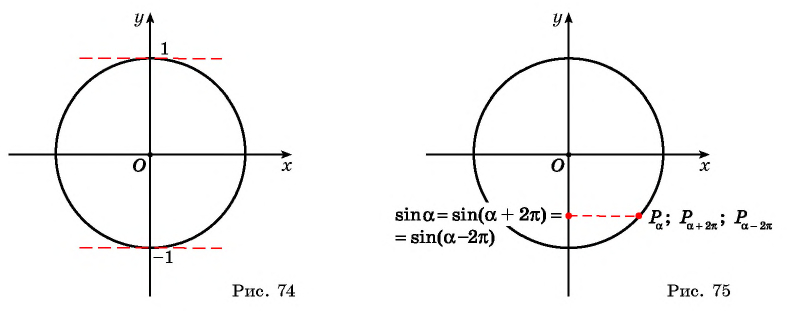
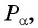
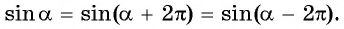
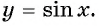
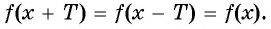
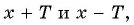 если
если 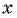 принадлежит области определения функции;
принадлежит области определения функции;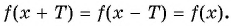
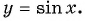
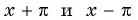 принадлежат области определения функции, так как
принадлежат области определения функции, так как 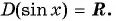
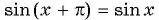 для всех
для всех 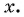
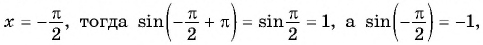
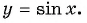
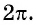
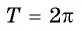
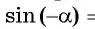
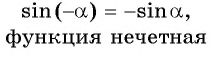
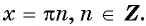
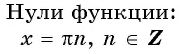
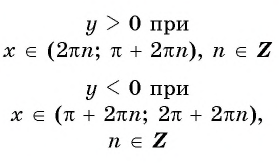
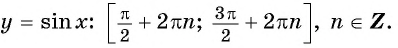
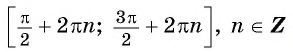
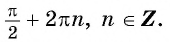
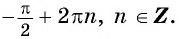
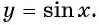
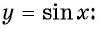
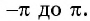
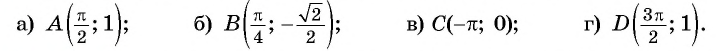
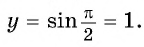
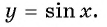
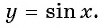
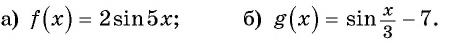
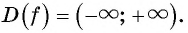
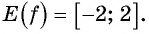
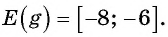
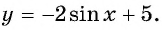
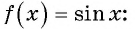
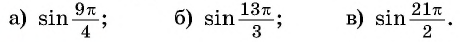
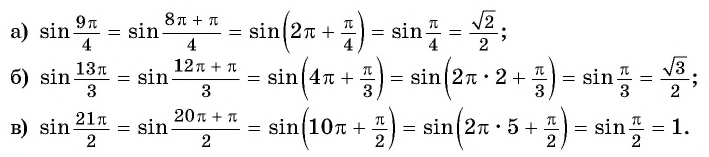
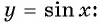
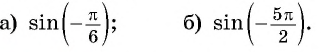
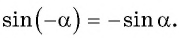
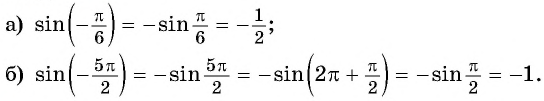
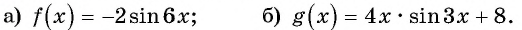
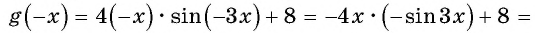
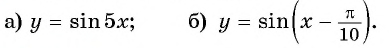
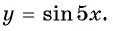
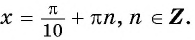
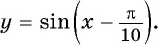
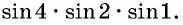
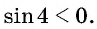
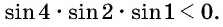
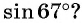
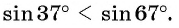







![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)