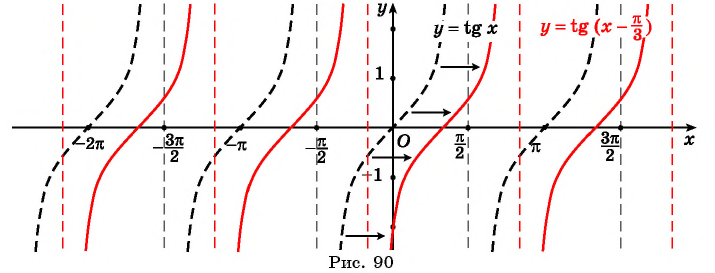
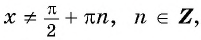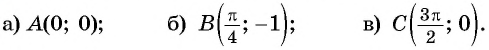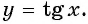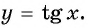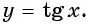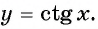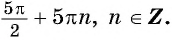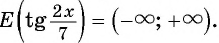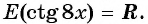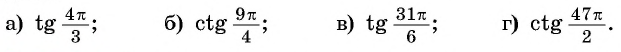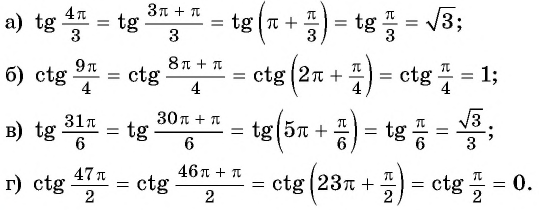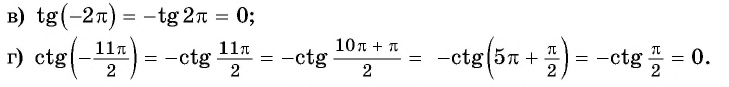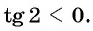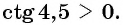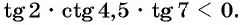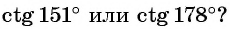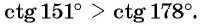- Развертка тангенса движения точки по числовой окружности в функцию от угла
- Свойства функции y=tgx
- Примеры
п.1. Развертка тангенса движения точки по числовой окружности в функцию от угла
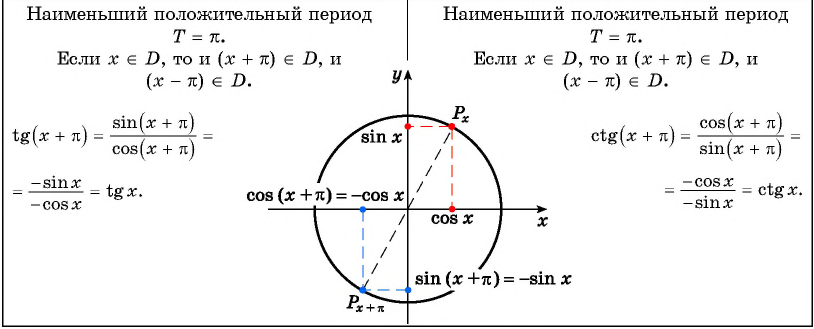
При движении точки по числовой окружности на вертикальной касательной, проведенной через точку (1;0), отображаются значения тангенсов соответствующих углов (см. §3 данного справочника).
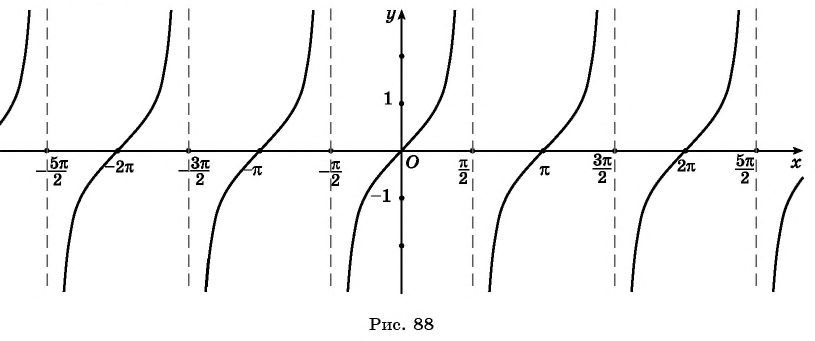
Рассмотрим, как изменяется тангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=tgx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.
В результате получаем график y=tgx для для всех x из области допустимых значений.
График y=tgx называют тангенцоидой.
Часть тангенцоиды c (-fracpi2lt xlt fracpi2) называют главной ветвью тангенцоиды.
п.2. Свойства функции y=tgx
1. Область определения (xnefracpi2+pi k) — множество действительных чисел, кроме точек, в которых (cosx=0).
2. Функция не ограничена сверху и снизу. Область значений (yinmathbb{R})
3. Функция нечётная $$ tg(-x)=-tgx $$
4. Функция периодическая с периодом π $$ tg(x+pi k)=tgx $$
5. Функция стремится к (+infty) при приближении слева к точкам (x=fracpi2+pi k).
Приближение к точке a слева записывается как (xrightarrow a-0) $$ lim_{xrightarrowfracpi2+pi k-0} tgx=+infty $$ Функция стремится к (-infty) при приближении справа к точкам (x=fracpi2+pi k).
Приближение к точке a справа записывается как (xrightarrow a+0) $$ lim_{xrightarrowfracpi2+pi k+0} tgx=-infty $$ Нули функции (y_{0}=0) достигаются в точках (x_0=pi k)
6. Функция возрастает на всей области определения.
7. Функция имеет разрывы в точках (x=fracpi2+pi k), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами (left(-fracpi2+pi k; fracpi2+pi kright)) функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=tgx на заданном промежутке:
a) (left[frac{2pi}{3}; frac{3pi}{2}right)) $$ y_{min}=tgleft(frac{2pi}{3}right)=-sqrt{3}, y_{max}=lim_{xrightarrowfrac{3pi}{2}-0}tgx=+infty $$ б) (left(frac{pi}{2}; piright]) $$ y_{min}=lim_{xrightarrowfrac{pi}{2}+0}tgx=-infty, y_{max}=tg(pi)=0 $$ в) (left[frac{3pi}{4}; frac{7pi}{6}right]) $$ y_{min}=tgleft(frac{3pi}{4}right)=-1, y_{max}=tgleft(frac{7pi}{6}right)=frac{1}{sqrt{3}} $$
Пример 2. Решите уравнение:
a) (tgx=-sqrt{3})
Бесконечное множество решений: (x=frac{2pi}{3}+pi k, kinmathbb{Z})
б) (tgleft(x-fracpi2right)=0)
(x-fracpi2=pi k)
Бесконечное множество решений: (x=frac{pi}{2}+pi k, kinmathbb{Z})
в) (tg(2x)=1)
(2x=fracpi4+pi k)
Бесконечное множество решений: (x=frac{pi}{8}+frac{pi k}{2}, kinmathbb{Z})
г) (tgleft(frac{x}{3}-1right)=-1)
(frac{x}{3}-1=-frac{pi}{4}+pi k)
(frac{x}{3}=1-frac{pi}{4}+pi k)
Бесконечное множество решений: (x=3-frac{3pi}{4}+3pi k, kinmathbb{Z})
Пример 3. Определите чётность функции: a) (y(x)=4tgx+5sinx)
$$ y(-x)=4tg(-x)+5sin(-x)=-4tgx-5sinx=-(4tgx+5sinx)=-y(x) $$ Функция нечётная.
б) (y(x)=tgx-2cosx)
$$ y(-x)=tg(-x)-2cos(-x)=-tgx-2cosx=-(tgx+2cosx)ne left[ begin{array} -y(x)\ y(x) end{array} right. $$ Функция ни чётная, ни нечётная.
в) (y(x)=tg^2x+cos5x)
$$ y(-x)=tg^2(-x)+cos(-5x)=(-tgx)^2+cos5x=tg^2x+cos5x)=y(x) $$ Функция чётная.
г) (y(x)=x^2-tgx)
$$ y(-x)=(-x)^2-tg(-x)=x^2+tgxne left[ begin{array} -y(x)\ y(x) end{array} right. $$ Функция ни чётная, ни нечётная.
Пример 4. Если (tg(7pi-x)=frac34), то чему равны (tgx, ctgx)?
Т.к. период тангенса равен π, получаем: begin{gather*} tg(7pi-x)=tg(-x)=-tgx=frac34Rightarrow tgx=-frac34\ ctgx=frac{1}{tgx}=-frac43 end{gather*} Ответ: (-frac34, -frac43)
Функция тангенса: формула, свойства, график
Содержание:
- Что такое тангенс
- Что такое функция тангенса: формула
- Свойства функции
- Как построить график
- Примеры решения задач
Что такое тангенс
Тангенсом какого-либо острого угла (alpha (tg alpha)) называют величину, выражающую отношение противоположного катета (а) к прилегающему катету (b) в треугольнике с углом 90°, то есть: (tg alpha = frac{a}{b})
Понятие тангенса угла можно проиллюстрировать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: microexcel.ru
Пример 1
Рассмотрим наглядный пример. Предположим, что катеты в треугольнике из определения тангенса имеют следующие значения: a = 3 b = 4 В таком случае справедливо записать выражение для расчета тангенса угла: (tg alpha = frac{a}{b} = frac{3}{4} = 0,75)
Что такое функция тангенса: формула
При решении задач можно нередко встретить примеры с тригонометрическими функциями, в том числе, функцией тангенса. Эта функция обладает специфическими свойствами, которые значительно упрощают вычисления. Запись имеет следующий вид:
(у = tg х)
Здесь х обозначает аргумент тригонометрической функции и играет роль независимой переменной, а у определяет непосредственно функцию, то есть зависимую переменную.
Свойства функции
С помощью знаний свойств функций в тригонометрии достаточно просто решать самые сложные и громоздкие примеры. Перечислим закономерности, характерные для функции тангенса:
- Функция тангенса определяется в области ((xnefracpi2+pi k)), то есть на множестве, в состав которого включены действительные числа, за исключением точек, характеризующихся нулевым значением для косинуса.
- Функция на графике не имеет ограничений в верхней и нижней части, поэтому ее область значений можно записать как (yinmathbb{R}).
- Функция тангенса является нечетной, что целесообразно записать в виде соотношения (tg(-x)=-tgx).
- Тригонометрическая функция тангенса является периодической, а ее период составляет pi. Таким образом:(tg(x+pi k)=tgx) .
- Стремление функции (к +infty) можно наблюдать при сближении с левой стороны с точками (x=fracpi2+pi k). Приближение к точке, обозначенной за a, слева формулируют таким образом: (xrightarrow) (a-0 lim_{xrightarrowfracpi2+pi k-0} tgx=+infty) .
- Стремление функции (к -infty) можно наблюдать при сближении с правой стороны с точками (x=fracpi2+pi k). Приближение к точке, обозначенной за а, справа следует зафиксировать как (xrightarrow) (a+0 lim_{xrightarrowfracpi2+pi k+0} tgx=-infty).
- Нули рассматриваемой функции (y_{0}=0) определены точками (x_0=pi k).
- Возрастание функции можно наблюдать на всей области, где она определена.
- Функция разрывается в точках (x=fracpi2+pi k), которые пересечены вертикальными асимптотами. На отрезках между ними функция не прерывается, то есть (left(-fracpi2+pi k; fracpi2+pi kright).)
- Функция не обладает максимальными и минимальными значениями.
Как построить график
Как и любую другую тригонометрическую функцию, тангенс достаточно просто изобразить в системе координат. Графическое изображение функции тангенса в обобщенном виде представлено на рисунке ниже:
Источник: microexcel.ru
Построить график функции тангенса несложно. Нужно лишь последовательно выполнять действия согласно стандартному алгоритму:
- определить контрольные точки для построения;
- начертить плавную кривую линию на плоскости координат;
- для выбранного промежутка построить значения, которые расположены симметрично по отношению к началу координат;
- так как для значений функции характерны повторы с некоторым периодом, то целесообразно скопировать график для каждого из промежутков области определения;
- в результате получен график под названием тангенсоида.
Примеры решения задач
Задача 1
Требуется путем применения свойств тригонометрической функции, изученных в теоретическом разделе, записать область определения для следующей функции: (y=text{tg}left( 2x+frac{pi }{3} right))
Решение
Зная, что функция тангенса не может быть определена в точках при нулевом значении косинуса, запишем справедливое соотношение и выполним необходимые преобразования:
(cos left( 2x+frac{pi }{3} right)=0)
(2x+frac{pi }{3}ne frac{pi }{2}+pi n,nin Z)
(xne frac{pi }{12}+frac{pi n}{2},nin Z)
В результате получена область, в которой определена функция из условия задания:
(D(y)=left( -frac{pi }{12}+frac{pi n}{2},frac{pi }{12}+frac{pi n}{2} right),nin Z)
Ответ: (D(y):xin left( -frac{pi }{12}+frac{pi n}{2},frac{pi }{12}+frac{pi n}{2} right),nin Z)
Задача 2
Дано уравнение, решение которого требуется найти: (sin 2x-sqrt{3}cos 2x=0)
Решение
Выполним преобразования исходного соотношения. В результате получим:
(sin 2x=sqrt{3}cos 2x)
После деления всех частей записи на выражение (cos 2x) соотношение изменится таким образом:
(text{tg}2x=sqrt{3})
При этом ОДЗ для полученного выражения примет следующий вид:
(left( -frac{pi }{4}+frac{pi n}{2},frac{pi }{4}+frac{pi n}{2} right),nin Z.)
Далее целесообразно приступить к решению уравнения:
(2=frac{pi }{3}+pi n,nin Z)
(x=frac{pi }{6}+frac{pi n}{2},nin Z)
Заметим, что корни, которые получились по итогам расчетов, соответствуют ОДЗ. Можно записать ответ.
Ответ: (x=frac{pi }{6}+frac{pi n}{2},nin Z)
Объяснение и обоснование
Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем
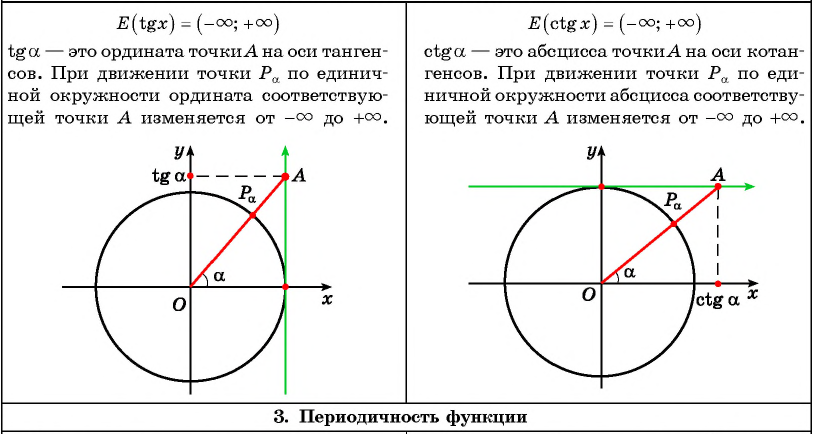
Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.
Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все
Значенияx входят в область определения функции y=tgx.
Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т
очек на линии тангенсов принимают
все значения до +, поскольку для любого действительного числа
мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит
внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку
(на самом деле их две). Следовательно, для любого действительного числа
найдется аргумент х, такой, что tan x равен данному действительному числу.
Поэтому область значений функции y= tg x — все действительные числа,
то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.
Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.
Тангенс — периодическая функция с наименьшим положительным периодом
Поэтому при построении графика
этой функции достаточно построить график на любом промежутке длиной π,
а потом полученную линию перенести параллельно вправо и влево вдоль оси
Ox на расстоянияkT = πk, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,
при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при
а также, учитывая период, при всех
Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,
Промежутки возрастания и убывания.
Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,
например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии
тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом
промежутке функция tgx возрастает. Учитывая периодичность функции
tgx, делаем вывод, что она возрастает также на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции y = tg x. Учитывая периодичность этой функции (с периодом π),
сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки
линии тангенсов. На рисунке 93 показано построение графика функции
y = tg x на промежутке.
Далее, учитывая периодичность тангенса (с периодом π), повторяем вид
графика на каждом промежутке длиной π (то есть параллельно переносим
график вдоль оси Ох на πk, где k — целое число).
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.
14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
Объяснение и обоснование
Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,
D (ctg x): x ≠ πk, k ∈ Z.
Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии
котангенсов (рис. 95).
.png)
Поскольку точки А и В единичной окружности лежат на прямых ОА
и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.
Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.
Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.
Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.
Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.
На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех
Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx< 0 при .
Промежутки возрастания и убывания
Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x2>x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx2<ctgx1), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков
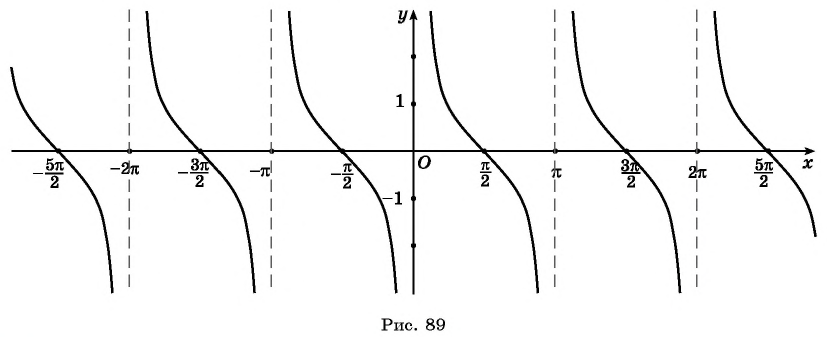
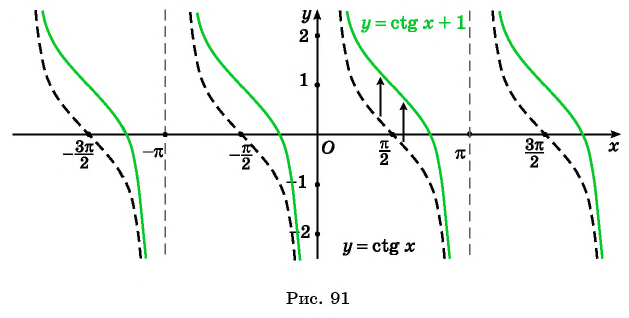
Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических преобразований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох. Получаем график, который называется котангенсоидой (рис. 98).
Функция
y=tgx
определена при
x≠π2+πn,n∈ℤ
, является нечётной и периодической с периодом
π
.
Используя эти свойства, строим её график на
0;π2
и затем выполняем соответствующие преобразования.
Выберем для построения контрольные точки, через которые проведём плавную кривую на координатной плоскости:
tg0=0;tgπ6=33;tgπ4=1;tgπ3=3.
Теперь для промежутка
−π2;0
построим симметричные относительно начала координат значения, получим график на промежутке
−π2;π2
.
Значения функции будут повторяться с периодом
π
, поэтому копируем построенную ветвь графика для каждого промежутка области определения.
График функции (y=tgx) называют тангенсоидой.
Главной ветвью графика функции (y=tgx) обычно называют ветвь, заключённую в полосе
−π2;π2
.
1. Область определения — множество всех действительных чисел
x≠π2+πn,n∈ℤ
.
2. Множество значений — множество
ℝ
всех действительных чисел.
3. Функция
y=tgx
периодическая с периодом
π
.
4. Функция
y=tgx
нечётная.
5. Функция
y=tgx
принимает:
— значение (0) при
x=πn,n∈ℤ;
— положительные значения на интервалах
πn;π2+πn,n∈ℤ;
— отрицательные значения на интервалах
−π2+πn;πn,n∈ℤ.
6. Функция
y=tgx
возрастает на интервалах
−π2+πn;π2+πn,n∈ℤ.
Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Определение функции y=tg x
Определение:
Зависимость, при которой каждому действительному числу 
Пример:
Определите, принадлежит ли графику функции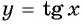 
точка:
Решение:
а) Подставим в формулу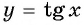 
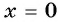
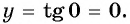
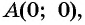
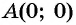
значение аргумента 
и найдем соответствующее значение функции 
Полученное значение функции равно ординате точки 
значит, точка 
принадлежит графику функции 
б) При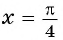 
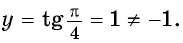
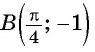
получим 
Точка 
не принадлежит графику функции 
в) При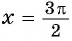 
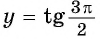
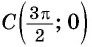
получим 
— не существует. Точка 
не принадлежит графику функции 
Определение функции y=ctg x
Определение:
Зависимость, при которой каждому действительному числу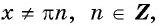 
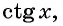
соответствует значение 
называется функцией 
Пример:
Верно ли, что график функции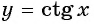 
проходит через точку:
Решение:
а) Подставим в формулу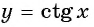 
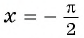
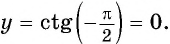
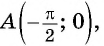
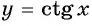
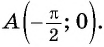
значение аргумента 
и найдем соответствующее значение функции 
Полученное значение функции равно ординате точки 
значит, график функции 
проходит через точку 
Верно.
б) При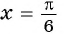 
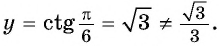
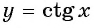
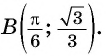
получим 
График функции 
не проходит через точку 
Неверно.
в) При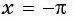 
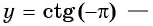
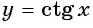
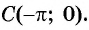
получим 
не существует. График функции 
не проходит через точку 
Неверно.
Свойства функций y=tg x и y=ctg x
Рассмотрим свойства этих функций:
График функции y=tg x
График функции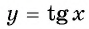 
изображен на рисунке 88. Он называется тангенсоидой.
График функции y=ctg x
График функции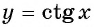 
изображен на рисунке 89. Этот график может быть получен путем преобразования графика функции 
Примеры заданий и их решения
Пример №1
Найдите область определения функции:
Решение:
а) Так как область определения функции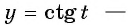 
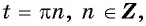
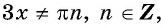
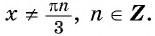
это все действительные числа, кроме чисел вида 
то 
значит, 
Таким образом, область определения данной функции — это все действительные числа, кроме чисел вида 
б) Областью определения функции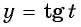 
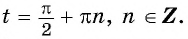
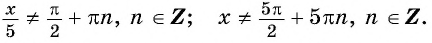
является множество всех действительных чисел, кроме чисел вида 
Значит, 
Область определения данной функции — это все действительные числа, кроме чисел вида 
Пример №2
Найдите множество значений функции:
Решение:
а) Так как множество значений функции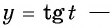 
это множество всех действительных чисел, то и 
б) Так как множество значений функции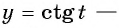 
это множество всех действительных чисел, то и 
Пример №3
Используя свойство периодичности функций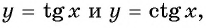 
найдите:
Решение:
Так как число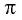 
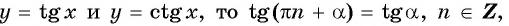
является наименьшим положительным периодом функций 
и 
Тогда:
- Заказать решение задач по высшей математике
Пример №4
Используя свойство нечетности функций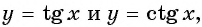 
найдите:
Решение:
Так как функции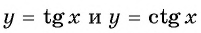 
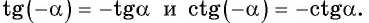
являются нечетными, то 
Тогда:
Пример №5
Определите знак произведения 
Решение:
Так как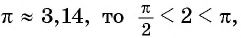 
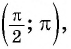
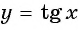
т. е. угол 2 радиана принадлежит промежутку 
на котором функция 
принимает отрицательные значения, значит, 
Угол 4,5 радиана принадлежит промежутку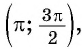 
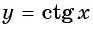
на котором функция 
принимает положительные значения, значит, 
Угол 7 радиан принадлежит промежутку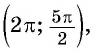 
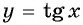
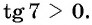
на котором функция 
принимает положительные значения, т. е. 
Значит, 
Пример №6
Что больше: 
Решение:
Поскольку углы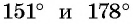 
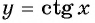
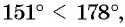
принадлежат промежутку 
на котором функция 
убывает и 
то 
Пример №7
Постройте график функции:
Решение:
а) График функции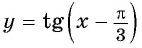 
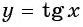
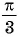
получаем сдвигом графика функции 
вдоль оси абсцисс на 
вправо (рис. 90).
б) График функции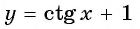 
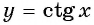
получаем сдвигом графика функции 
вдоль оси ординат на 1 единицу вверх (рис. 91).
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график