In this Python tutorial, you’ll learn to search a string in a text file. Also, we’ll see how to search a string in a file and print its line and line number.
After reading this article, you’ll learn the following cases.
- If a file is small, read it into a string and use the
find()method to check if a string or word is present in a file. (easier and faster than reading and checking line per line) - If a file is large, use the mmap to search a string in a file. We don’t need to read the whole file in memory, which will make our solution memory efficient.
- Search a string in multiple files
- Search file for a list of strings
We will see each solution one by one.
Table of contents
- How to Search for a String in Text File
- Example to search for a string in text file
- Search file for a string and Print its line and line number
- Efficient way to search string in a large text file
- mmap to search for a string in text file
- Search string in multiple files
- Search file for a list of strings
How to Search for a String in Text File
Use the file read() method and string class find() method to search for a string in a text file. Here are the steps.
- Open file in a read mode
Open a file by setting a file path and access mode to the
open()function. The access mode specifies the operation you wanted to perform on the file, such as reading or writing. For example, r is for reading.fp= open(r'file_path', 'r') - Read content from a file
Once opened, read all content of a file using the
read()method. Theread()method returns the entire file content in string format. - Search for a string in a file
Use the
find()method of a str class to check the given string or word present in the result returned by theread()method. Thefind()method. The find() method will return -1 if the given text is not present in a file - Print line and line number
If you need line and line numbers, use the
readlines() method instead ofread()method. Use the for loop andreadlines()method to iterate each line from a file. Next, In each iteration of a loop, use the if condition to check if a string is present in a current line and print the current line and line number
Example to search for a string in text file
I have a ‘sales.txt’ file that contains monthly sales data of items. I want the sales data of a specific item. Let’s see how to search particular item data in a sales file.
def search_str(file_path, word):
with open(file_path, 'r') as file:
# read all content of a file
content = file.read()
# check if string present in a file
if word in content:
print('string exist in a file')
else:
print('string does not exist in a file')
search_str(r'E:demosfiles_demosaccountsales.txt', 'laptop')Output:
string exists in a file
Search file for a string and Print its line and line number
Use the following steps if you are searching a particular text or a word in a file, and you want to print a line number and line in which it is present.
- Open a file in a read mode.
- Next, use the
readlines()method to get all lines from a file in the form of a list object. - Next, use a loop to iterate each line from a file.
- Next, In each iteration of a loop, use the if condition to check if a string is present in a current line and print the current line and line number.
Example: In this example, we’ll search the string ‘laptop’ in a file, print its line along with the line number.
# string to search in file
word = 'laptop'
with open(r'E:demosfiles_demosaccountsales.txt', 'r') as fp:
# read all lines in a list
lines = fp.readlines()
for line in lines:
# check if string present on a current line
if line.find(word) != -1:
print(word, 'string exists in file')
print('Line Number:', lines.index(line))
print('Line:', line)Output:
laptop string exists in a file line: laptop 10 15000 line number: 1
Note: You can also use the readline() method instead of readlines() to read a file line by line, stop when you’ve gotten to the lines you want. Using this technique, we don’t need to read the entire file.
Efficient way to search string in a large text file
All above way read the entire file in memory. If the file is large, reading the whole file in memory is not ideal.
In this section, we’ll see the fastest and most memory-efficient way to search a string in a large text file.
- Open a file in read mode
- Use for loop with
enumerate()function to get a line and its number. Theenumerate()function adds a counter to an iterable and returns it in enumerate object. Pass the file pointer returned by theopen()function to theenumerate(). - We can use this enumerate object with a for loop to access the each line and line number.
Note: The enumerate(file_pointer) doesn’t load the entire file in memory, so this is an efficient solution.
Example:
with open(r"E:demosfiles_demosaccountsales.txt", 'r') as fp:
for l_no, line in enumerate(fp):
# search string
if 'laptop' in line:
print('string found in a file')
print('Line Number:', l_no)
print('Line:', line)
# don't look for next lines
breakExample:
string found in a file Line Number: 1 Line: laptop 10 15000
mmap to search for a string in text file
In this section, we’ll see the fastest and most memory-efficient way to search a string in a large text file.
Also, you can use the mmap module to find a string in a huge file. The mmap.mmap() method creates a bytearray object that checks the underlying file instead of reading the whole file in memory.
Example:
import mmap
with open(r'E:demosfiles_demosaccountsales.txt', 'rb', 0) as file:
s = mmap.mmap(file.fileno(), 0, access=mmap.ACCESS_READ)
if s.find(b'laptop') != -1:
print('string exist in a file')Output:
string exist in a file
Search string in multiple files
Sometimes you want to search a string in multiple files present in a directory. Use the below steps to search a text in all files of a directory.
- List all files of a directory
- Read each file one by one
- Next, search for a word in the given file. If found, stop reading the files.
Example:
import os
dir_path = r'E:demosfiles_demosaccount'
# iterate each file in a directory
for file in os.listdir(dir_path):
cur_path = os.path.join(dir_path, file)
# check if it is a file
if os.path.isfile(cur_path):
with open(cur_path, 'r') as file:
# read all content of a file and search string
if 'laptop' in file.read():
print('string found')
breakOutput:
string found
Search file for a list of strings
Sometimes you want to search a file for multiple strings. The below example shows how to search a text file for any words in a list.
Example:
words = ['laptop', 'phone']
with open(r'E:demosfiles_demosaccountsales.txt', 'r') as f:
content = f.read()
# Iterate list to find each word
for word in words:
if word in content:
print('string exist in a file')Output:
string exist in a file
Python Exercises and Quizzes
Free coding exercises and quizzes cover Python basics, data structure, data analytics, and more.
- 15+ Topic-specific Exercises and Quizzes
- Each Exercise contains 10 questions
- Each Quiz contains 12-15 MCQ
The reason why you always got True has already been given, so I’ll just offer another suggestion:
If your file is not too large, you can read it into a string, and just use that (easier and often faster than reading and checking line per line):
with open('example.txt') as f:
if 'blabla' in f.read():
print("true")
Another trick: you can alleviate the possible memory problems by using mmap.mmap() to create a «string-like» object that uses the underlying file (instead of reading the whole file in memory):
import mmap
with open('example.txt') as f:
s = mmap.mmap(f.fileno(), 0, access=mmap.ACCESS_READ)
if s.find('blabla') != -1:
print('true')
NOTE: in python 3, mmaps behave like bytearray objects rather than strings, so the subsequence you look for with find() has to be a bytes object rather than a string as well, eg. s.find(b'blabla'):
#!/usr/bin/env python3
import mmap
with open('example.txt', 'rb', 0) as file,
mmap.mmap(file.fileno(), 0, access=mmap.ACCESS_READ) as s:
if s.find(b'blabla') != -1:
print('true')
You could also use regular expressions on mmap e.g., case-insensitive search: if re.search(br'(?i)blabla', s):
В прошлой статье я рассказывала, что составила для своего проекта словарь «Властелина Колец», причем для каждого англоязычного терма (слова/словосочетания) хранится перевод и список глав, в которых встречается это выражение. Все это составлено вручную. Однако мне не дает покоя, что многие вхождения термов могли быть пропущены.
В первой версии MVP я частично решила эту проблему обычным поиском по подстроке (b{term}, где b – граница слова), что позволило найти вхождения отдельных слов без учета морфологии или с некоторыми внешними флексиями (например, -s, -ed, -ing). Фактически это поиск подстроки с джокером на конце. Но для многословных выражений и неправильных глаголов, составляющих весомую долю моего словаря, этот способ не работал.
После пары безуспешных попыток установить Elasticsearch я, как типичный изобретатель велосипеда и вечного двигателя, решила писать свой код. Скудным словообразованием английского языка меня не запугать ввиду наличия опыта разработки полнотекстового поиска по документам на великом и могучем русском языке. Кроме того, для моей задачи часть вхождений уже все равно выбрана вручную и потому стопроцентная точность не требуется.
Подготовка словаря
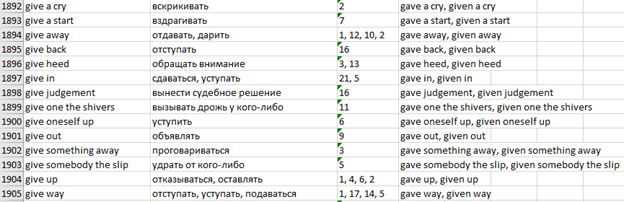
Итак, дан словарь. Ну как дан – составлен руками за несколько месяцев упорного труда. Дан с точки зрения программиста. После прошлой статьи словарь подрос вдвое и теперь охватывает весь первый том («Братство Кольца»). В сыром виде состоит из 11.690 записей в формате «терм – перевод – номер главы». Хранится в Excel.
Как и в прошлый раз, я сгруппировала свой словарь по словарным гнездам с помощью функции pivot_table() из pandas. Осталось 5.404 записи, а после ручного редактирования — 5.354.
Больше всего меня беспокоили неправильные глаголы, поскольку в моем словаре они хранились в инфинитиве, а в романе чаще всего употреблялись в прошедшем времени. Ввиду так называемого аблаута (например, run – ran – run) установить инфинитив по словоформе прошедшего времени невозможно.
Я скачала словарь неправильных глаголов. Он насчитывал 294 штуки, многие из которых допускали два варианта. Пришлось проверить все вариации по тексту Толкиена, чтобы установить, какая форма характерна для его речи: например, cloven (p.p. от cleave) вместо cleft (что у него существительное). Оказалось, что многие неправильные глаголы у него правильные (например, burn), а leap даже существует в обеих версиях — leaped и leapt.
Теперь вариации неправильных глаголов унифицированы, а их список хранится в обычном текстовом файле:
Остается считать этот файл в датафрейм с помощью функции read_csv(), указав в качестве разделителей пробелы:
import pandas as pd
verb_data = pd.read_csv(pathlib.Path('c:/', 'ALL', 'LotR', 'неправильные глаголы.txt'),
sep=" ", header=None, names=["Inf", "Past", "PastParticiple"], index_col=0)Явно задаем index_col, чтобы сделать индексом первый столбец, хранящий инфинитивы глаголов, для удобства дальнейшего поиска.
Считаем наш главный словарь в другой датафрейм:
excel_data = pd.read_excel(pathlib.Path('c:/', 'ALL', 'LotR', 'словарь Толкиена сведенный.xlsx'), dtype = str)
df = pd.DataFrame(excel_data, columns=['Word', 'Russian', 'Chapters'])Теперь объявим функцию, которая для каждого словарного терма проверит наличие в нем неправильного глагола и в зависимости от результата сгенерирует словоформы. Для простоты будем считать, что неправильный глагол всегда стоит на первом месте.
def check_irrverbs(word):
global verb_data
# берем часть выражения до первого пробела
arr = word.split(' ')
w, *tail = arr # = arr[0], arr[1:]
# запоминаем хвост
tail = " ".join(tail)
# проверяем, не является ли она неправильным глаголом
if w in verb_data.index:
# формируем формы Past и Past Participle
# если они одинаковые, то достаточно хранить одну форму
if verb_data.loc[w]["Past"] == verb_data.loc[w]["PastParticiple"]:
return verb_data.loc[w]["Past"] + " " + tail
return ", ".join([v + " " + tail for v in verb_data.loc[w].tolist()])
return ""Таким образом, для выражения make up one’s mind функция вернет made up one’s mind.
Применяем функцию к датафрейму, сохраняя результаты в новый столбец, и затем экспортируем результат в новый Excel-файл:
df['IrrVerb'] = df['Word'].apply(check_irrverbs)
df.to_excel(pathlib.Path('c:/', 'ALL', 'LotR', 'словарь Толкиена сведенный.xlsx'))Теперь в Excel-таблице появился новый столбец, хранящий 2-ю (Past) и 3-ю (Past Participle) формы для всех неправильных глаголов, а для правильных столбец пуст.
Всего таких записей оказалось 662.
Спряжение потенциальных глаголов
Теперь сгенерируем все формы и для правильных, и для неправильных глаголов.
def generate_verbs(word, is_irrverb):
forms = []
# взять часть выражения до первого пробела
verb, tail = word, ""
pos = word.find(" ")
if pos >= 0:
verb = word[:pos]
tail = word[pos:]
consonant = "bcdfghjklmnpqrstvwxz"
last = verb[-1]
# глагол во 2 и 3 формах
if not is_irrverb:
if last in consonant:
forms.append(verb + last + "ed" + tail) # stop -> stopped
forms.append(verb + "ed" + tail) # и вариант без удвоения
elif last == "y":
if verb[-2] in consonant:
forms.append(verb[:-1] + "ied" + tail) # carry -> carried
else:
forms.append(verb + "ed" + tail) # play -> played
elif last == "e":
forms.append(verb + "d" + tail) # arrive -> arrived
else:
forms.append(verb + "ed" + tail)
# герундий, он же ing-овая форма глагола
if verb[-2:] == "ie":
forms.append(verb[:-2] + "ying" + tail) # lie -> lying
elif last == "e":
forms.append(verb[:-1] + "ing" + tail) # write -> writing
elif last in consonant:
forms.append(verb + last + "ing" + tail) # sit -> sitting
forms.append(verb + "ing" + tail) # sit -> sitting
else:
forms.append(verb + "ing" + tail)
return formsКак и прежде, для простоты будем считать глаголом часть выражения до первого пробела либо все выражение целиком, если оно не содержит пробелов. Посмотрим, на какую букву (переменная last) оканчивается предполагаемый глагол. Для этого нужен список либо гласных, либо согласных. Список гласных был бы короче, но так как нам понадобится проверять именно на согласную, то нагляднее будет хранить список consonant.
Для правильных глаголов вторая и третья формы создаются путем прибавления флексий -d, -ed, -ied в зависимости от последнего и предпоследнего звука. Так как учитывается еще и ударение, то проще всего сгенерировать оба варианта, из которых грамматически корректен будет только один. Для неправильных глаголов мы уже нашли обе формы и записали в отдельный столбец.
Герундий образуется одинаково для правильных и неправильных глаголов, но опять-таки надо учитывать последний символ и ударение, поэтому снова создаем оба варианта.
Все варианты записываются в список forms, который функция и возвращает.
Сложность заключается в том, что наш словарь не содержит информации о частях речи для каждого терма, да это и малоинформативно ввиду так называемой конверсии – одно и то же слово может быть и существительным, и глаголом в зависимости от места в предложении. Поэтому мы сейчас рассматриваем все хранящиеся в словаре выражения как потенциальные глаголы, так как перед нами не стоит задача построить грамматически корректную форму. Мы строим просто гипотезы. Если они не найдутся в тексте, то и не надо.
Подстановки
Кроме неправильных глаголов, словарь содержит еще один вид выражений, осложняющих полнотекстовый поиск, — подстановочные местоимения: притяжательное one’s, возвратное oneself и неопределенные somebody и something. В реальном тексте они должны заменяться на конкретные слова – соответственно, притяжательные местоимения (my, your, his и т.д.), возвратные местоимения (myself, yourself, himself и т.д.) и существительные. Поэтому надо сгенерировать все возможные формы с подстановками.
Начнем с one’s и oneself:
def replace_possessive_reflexive(word):
possessive = ["my", "mine", "your", "yours", "his", "her", "hers", "its", "our", "ours", "their", "theirs"]
reflexive = ["myself", "yourself", "himself", "herself", "itself", "ourselves", "yourselves", "themselves"]
# заменить one's на все варианты из possessive
if "one's" in word:
forms = list(map(lambda p: word.replace("one's", p), possessive))
elif "oneself" in word:
# заменить oneself на все варианты из reflexive
forms = list(map(lambda r: word.replace("oneself", r), reflexive))
else:
forms = [word]
return formsЗдесь мы для простоты предполагаем, что one’s и oneself не встречаются в одном выражении, а также не употребляются в реальном тексте. Если в терме есть одно из этих слов, то он интересует нас только с подстановками. В противном случае терм рассматривается как одна из форм самого себя, поэтому создается список, состоящий только из него.
Полный процесс замены обрабатывает также скобки и неопределенные местоимения:
def template_replace(word):
forms = []
forms = [word] if not "(" in word else [word.replace("(", "").replace(")", ""), re.sub("([^)]+)", "", word)]
forms = list(map(lambda f: f.replace("somebody", "S+").replace("something", "S+"), forms))
forms = list(map(replace_possessive_reflexive, forms))
return sum(forms, [])Замена происходит в три этапа, причем результат предыдущего подается на вход следующему.
-
Если терм содержит скобки, то рассматриваем два варианта – с их содержимым или без него: например, wild(ly) -> {wild, wildly}.
-
Что касается somebody и something, то они заменяются на S+ – группу любых непробельных символов, то есть на заготовку для будущего регулярного выражения.
-
Наконец вызываем рассмотренную выше функцию replace_possessive_reflexive() для обработки one’s и oneself.
В итоге получится многомерный список, который необходимо преобразовать в одномерный. В данном случае эта задача решается путем сложения с пустым списком.
Таким образом, основная идея данной реализации полнотекстового поиска – генерировать максимальное количество вариантов словоформ, чтобы затем искать их в тексте. Как велико это число? В простейшем случае, для термов, не содержащих неправильных глаголов и оканчивающихся на гласную, будет всего 3 формы – инфинитив, вторая/третья форма и герундий. Если терм кончается на согласную, то появляется второй вариант герундия. В худшем случае терм содержит скобки, притяжательное местоимение и неправильный глагол, оканчиваясь на согласную, тогда для первичного списка из 2 вариантов со скобками * 12 притяжательных местоимений будут сгенерированы по 24 формы инфинитива, двух вариантов герундия, а также прошедшего времени и причастия прошедшего времени, итого
Отдельной строкой, чтобы осознать масштаб этой цифры)
Впрочем, мой словарь не содержит настолько сложных случаев. Вот более характерный пример – hold one’s breath (сочетание неправильного глагола, оканчивающегося на гласную, и притяжательного местоимения). Из него будет сгенерировано 48 форм:
-
12 вариантов инфинитива: ‘hold my breath’, ‘hold mine breath’, ‘hold your breath’, ‘hold yours breath’, ‘hold his breath’, ‘hold her breath’, ‘hold hers breath’, ‘hold its breath’, ‘hold our breath’, ‘hold ours breath’, ‘hold their breath’, ‘hold theirs breath’
-
24 варианта герундия, с удвоенной согласной и с одинарной: ‘holdding my breath’, ‘holding my breath’, ‘holdding mine breath’, ‘holding mine breath’, ‘holdding your breath’, ‘holding your breath’, ‘holdding yours breath’, ‘holding yours breath’, ‘holdding his breath’, ‘holding his breath’, ‘holdding her breath’, ‘holding her breath’, ‘holdding hers breath’, ‘holding hers breath’, ‘holdding its breath’, ‘holding its breath’, ‘holdding our breath’, ‘holding our breath’, ‘holdding ours breath’, ‘holding ours breath’, ‘holdding their breath’, ‘holding their breath’, ‘holdding theirs breath’, ‘holding theirs breath’
-
12 вариантов прошедшего времени, совпадающего с past participle: ‘held my breath’, ‘held mine breath’, ‘held your breath’, ‘held yours breath’, ‘held his breath’, ‘held her breath’, ‘held hers breath’, ‘held its breath’, ‘held our breath’, ‘held ours breath’, ‘held their breath’, ‘held theirs breath’
Такие случаи довольно редки. Как уже говорилось, на весь 5-тысячный словарь нашлось всего 662 строки с неправильными глаголами. Что касается остальных сложных случаев, то в словаре 91 терм с притяжательными местоимениями, 31 – с подстановками somebody/something и 61 совмещает в себе и неправильный глагол, и какую-либо подстановку.
Поиск по тексту
Наконец приступаем к анализу оригинального текста, чтобы найти в нем пропущенные вхождения термов. Считаем датафрейм из Excel, не забывая, что заданные в списке columns заголовки столбцов должны фигурировать в первой строке листа Excel.
excel_data = pd.read_excel(pathlib.Path('c:/', 'ALL', 'LotR', 'словарь Толкиена сведенный.xlsx'), dtype = str)
df = pd.DataFrame(excel_data, columns=['Word', 'Russian', 'Chapters', 'IrrVerb'])Прежде чем работать с текстом романа, возьмем на себя смелость слегка подправить великого автора, изменив нумерацию глав на сквозную. Вместо двух книг по 12 и 10 глав соответственно получится одна с 22-мя главами.
После этого откроем текст, удалим символы перевода строки и табуляции. Сразу заменим часто встречающееся в нем слово Mr., чтобы оно не мешало разбивать текст по предложениям.
f = open(pathlib.Path('c:/', 'ALL', 'LotR', 'Fellowship.txt'))
text = f.read().replace('n', ' ').replace('t', ' ').replace('r', ' ').replace('Mr. ', 'Mr') # учтет Mr.BagginsТеперь разобьем текст по главам.
lotr = []
text = re.split('Chaptersd+', text)Тогда в 0-м элементе списка будет предисловие, в 1-м — глава 1 и т.д., то есть индексы будут соответствовать реальным номерам глав, что очень удобно.
for chapter in text:
lotr.append(re.split('[.?!]', chapter))Теперь нас ждет главная функция, обрабатывающая строку датафрейма. Прежде всего получим старый список глав, в которых встречается данный терм. Он хранится в отдельном столбце таблицы. Наша задача — постараться дополнить этот список и в любом случае не забыть хотя бы отсортировать его.
ch = list(map(int, vec[0].split(',')))Если терм оканчивается восклицательным или вопросительным знаком, то это неизменяемое устойчивое выражение, например, междометие. Для него никаких словоформ искать не нужно.
word = vec[1]
if word[-1:] == "!" or word[-1:] == "?":
forms = [word]Для любого другого терма начнем с проверки, входит ли в него неправильный глагол, то есть заполнен ли соответствующий столбец (isnan()). Для неправильного глагола выделим 2-ю и 3-ю формы, которые могут различаться или совпадать.
else:
is_irrverb = False if isinstance(vec[2], float) and math.isnan(vec[2]) else True
if is_irrverb:
pos = vec[2].find(", ")
if pos >= 0:
past = vec[2][:pos]
past_participle = vec[2][pos + 2:]
else:
past = past_participle = vec[2]Произведем замены с помощью функции template_replace(), получим список словоформ. Проспрягаем каждый элемент этого списка.
forms = template_replace(word)
forms = forms + sum(list(map(lambda f: generate_verbs(f, is_irrverb), forms)), [])Для неправильных глаголов отдельно произведем замены для 2-й и 3-й форм.
if is_irrverb:
forms = forms + template_replace(past)
if past_participle != past:
forms = forms + template_replace(past_participle)Затем ищем каждую словоформу в каждой главе кроме ранее найденных глав, содержащихся в старом списке ch. Для этого используем функцию filter(), передав ей лямбда-функцию, которая будет обрабатывать каждое предложение. Поиск производится по регулярному выражению b{f}, где b — граница слова, а f — словоформа. Как уже говорилось, указание левой границы слова позволяет реализовать поиск с джокером на конце подстроки. Несмотря на весь написанный ранее код, мы все еще нуждаемся в этом нехитром приеме, так как флексии никто не отменял. Кроме того, от регулярного выражения мы никуда не денемся, так как ранее заменяли somebody/something на S+.
for f in forms:
for i in range(1, len(lotr)): # 0-ю главу (предисловие) пока пропускаем
if not i in ch:
match = list(filter(lambda sentence: re.search(rf'b{f}', sentence, flags=re.IGNORECASE), lotr[i]))
if match:
ch.append(i)Этот код ищет все вхождения терма в главу, хотя для поставленной задачи нужно найти только первое. Зато этот вариант облегчает тестирование программы.
Новые номера глав сохраняются в тот же список ch, который в конце концов сортируется и возвращается.
ch.sort()
return chПолный код функции check_chapters() выглядит следующим образом.
def check_chapters(vec):
global lotr
ch = list(map(int, vec[0].split(',')))
word = vec[1]
if word[-1:] == "!" or word[-1:] == "?":
forms = [word]
else:
is_irrverb = False if isinstance(vec[2], float) and math.isnan(vec[2]) else True
if is_irrverb:
pos = vec[2].find(", ")
if pos >= 0:
past = vec[2][:pos]
past_participle = vec[2][pos + 2:]
else:
past = past_participle = vec[2]
forms = template_replace(word)
forms = forms + sum(list(map(lambda f: generate_verbs(f, is_irrverb), forms)), [])
if is_irrverb:
forms = forms + template_replace(past)
if past_participle != past:
forms = forms + template_replace(past_participle)
for f in forms:
for i in range(1, len(lotr)): # 0-ю главу (предисловие) пока пропускаем
if not i in ch:
match = list(filter(lambda sentence: re.search(rf'b{f}', sentence, flags=re.IGNORECASE), lotr[i]))
if match:
ch.append(i)
ch.sort()
return chОсталось только применить эту функцию к датафрейму, сохранив результат в новый столбец New chapters:
df['New chapters'] = df[['Chapters', 'Word', 'IrrVerb']].apply(check_chapters, axis=1)
df.to_excel(pathlib.Path('c:/', 'ALL', 'LotR', 'словарь Толкиена сведенный.xlsx'))Тестирование
Для тестирования была произведена выборка наиболее сложных термов – с неправильными глаголами и подстановками.
test = df[['Chapters', 'Word', 'IrrVerb']]
test = test[(test['IrrVerb'].str.len() > 0) & (test['Word'].str.contains("one's") | test['Word'].str.contains("something") | test['Word'].str.contains("somebody"))]
print(test.apply(check_chapters, axis=1))Вот термы, для которых было найдено более одного вхождения и которые поэтому являются самыми характерными (неупорядоченная нумерация сложилась потому, что поиск производился сначала по словоформам и лишь затем по главам):
|
Терм |
Найденные вхождения |
|
find one’s way |
Chapter 12: We could perhaps find our way through and come round to Rivendell from the north; but it would take too long, for I do not know the way, and our food would not last Chapter 2: He found his way into Mirkwood, as one would expect |
|
make one’s way |
Chapter 3: My plan was to leave the Shire secretly, and make my way to Rivendell; but now my footsteps are dogged, before ever I get to Buckland Chapter 16: Make your ways to places where you can find grass, and so come in time to Elrond’s house, or wherever you wish to go Chapter 6: Coming to the opening they found that they had made their way down through a cleft in a high sleep bank, almost a cliff Chapter 11: Merry’s ponies had escaped altogether, and eventually (having a good deal of sense) they made their way to the Downs in search of Fatty Lumpkin Chapter 12: They made their way slowly and cautiously round the south-western slopes of the hill, and came in a little while to the edge of the Road |
|
make up one’s mind |
Chapter 10: You must make up your mind Chapter 19: But before Sam could make up his mind what it was that he saw, the light faded; and now he thought he saw Frodo with a pale face lying fast asleep under a great dark cliff Chapter 16: The eastern arch will probably prove to be the way that we must take; but before we make up our minds we ought to look about us Chapter 22: ‘Yet we must needs make up our minds without his aid Chapter 4: I am leaving the Shire as soon as ever I can – in fact I have made up my mind now not even to wait a day at Crickhollow, if it can be helped Chapter 21: Sam had long ago made up his mind that, though boats were maybe not as dangerous as he had been brought up to believe, they were far more uncomfortable than even he had imagined |
|
one’s heart sink |
Chapter 11: ‘It is getting late, and I don’t like this hole: it makes my heart sink somehow Chapter 14: » ‘»The Shire,» I said; but my heart sank |
|
shake one’s head |
Chapter 2: ‘They are sailing, sailing, sailing over the Sea, they are going into the West and leaving us,’ said Sam, half chanting the words, shaking his head sadly and solemnly Chapter 4: Too near the River,’ he said, shaking his head Chapter 9: ‘ ‘There’s some mistake somewhere,’ said Butterbur, shaking his head Chapter 14: ‘ he said, shaking his head Chapter 16: ‘I am too weary to decide,’ he said, shaking his head Chapter 12: ‘ When he heard what Frodo had to tell, he became full of concern, and shook his head and sighed Chapter 15: Gimli looked up and shook his head Chapter 22: Sam, who had been watching his master with great concern, shook his head and muttered: ‘Plain as a pikestaff it is, but it’s no good Sam Gamgee putting in his spoke just now |
|
sleep on something |
Chapter 3: ‘Well, see you later – the day after tomorrow, if you don’t go to sleep on the way Chapter 13: His head seemed sunk in sleep on his breast, and a fold of his dark cloak was drawn over his face Chapter 18: I cannot sleep on a perch |
|
spring to one’s feet |
Chapter 2: ’ cried Gandalf, springing to his feet Chapter 11: ‘ asked Frodo, springing to his feet Chapter 14: ‘ cried Frodo in amazement, springing to his feet, as if he expected the Ring to be demanded at once Chapter 16: With a suddenness that startled them all the wizard sprang to his feet Chapter 8: The hobbits sprang to their feet in alarm, and ran to the western rim Chapter 9: The local hobbits stared in amazement, and then sprang to their feet and shouted for Barliman |
|
take one’s advice |
Chapter 3: If I take your advice I may not see Gandalf for a long while, and I ought to know what is the danger that pursues me Chapter 11: When they saw them they were glad that they had taken his advice: the windows had been forced open and were swinging, and the curtains were flapping; the beds were tossed about, and the bolsters slashed and flung upon the floor; the brown mat was torn to pieces |
Таким образом, в большинстве случаев словоформы обрабатываются корректно.
Итоги
Учитывая вышеприведенный расчет со 120 словоформами, порожденными одной строкой словаря, поиск всех вхождений вместо первого, наличие регулярных выражений и громоздкость решения в целом, я не ожидала от программы быстрых результатов. Однако на ноутбуке с 4-ядерным Intel i5-8265U и 8 Гб ОЗУ словарь из 5 тыс. строк был проработан за 1.187 секунд. В итоге найдены 3.330 новых вхождений в дополнение к прежним 10.482, записанным вручную.
Вот так несколько десятков строк кода показали вполне удовлетворительные результаты для полнотекстового поиска с поддержкой морфологии английского языка. Программа работает достаточно корректно и быстро. Конечно, она не лишена недостатков — не застрахована от ложных срабатываний, не учтет флексию в середине многословного терма (например, takes his advice). Однако с поставленной задачей успешно справилась.
In this article, we will learn how we can replace text in a file using python.
Method 1: Searching and replacing text without using any external module
Let see how we can search and replace text in a text file. First, we create a text file in which we want to search and replace text. Let this file be SampleFile.txt with the following contents:
To replace text in a file we are going to open the file in read-only using the open() function. Then we will t=read and replace the content in the text file using the read() and replace() functions.
Syntax: open(file, mode=’r’)
Parameters:
- file : Location of the file
- mode : Mode in which you want toopen the file.
Then we will open the same file in write mode to write the replaced content.
Python3
search_text = "dummy"
replace_text = "replaced"
with open(r'SampleFile.txt', 'r') as file:
data = file.read()
data = data.replace(search_text, replace_text)
with open(r'SampleFile.txt', 'w') as file:
file.write(data)
print("Text replaced")
Output:
Text replaced
Method 2: Searching and replacing text using the pathlib2 module
Let see how we can search and replace text using the pathlib2 module. First, we create a Text file in which we want to search and replace text. Let this file be SampleFile.txt with the following contents:
Install pathlib2 module using the below command:
pip install pathlib2
This module offers classes representing filesystem paths with semantics appropriate for different operating systems. To replace the text using pathlib2 module we will use the Path method of pathlib2 module.
Syntax: Path(file)
Parameters:
- file: Location of the file you want to open
In the below code we are replacing “dummy” with “replaced” in our text file. using the pathlib2 module.
Code:
Python3
from pathlib2 import Path
def replacetext(search_text, replace_text):
file = Path(r"SampleFile.txt")
data = file.read_text()
data = data.replace(search_text, replace_text)
file.write_text(data)
return "Text replaced"
search_text = "dummy"
replace_text = "replaced"
print(replacetext(search_text, replace_text))
Output:
Text replaced
Method 3: Searching and replacing text using the regex module
Let see how we can search and replace text using the regex module. We are going to use the re.sub( ) method to replace the text.
Syntax: re.sub(pattern, repl, string, count=0, flags=0)
Parameters:
- repl : Text you want to add
- string : Text you want to replace
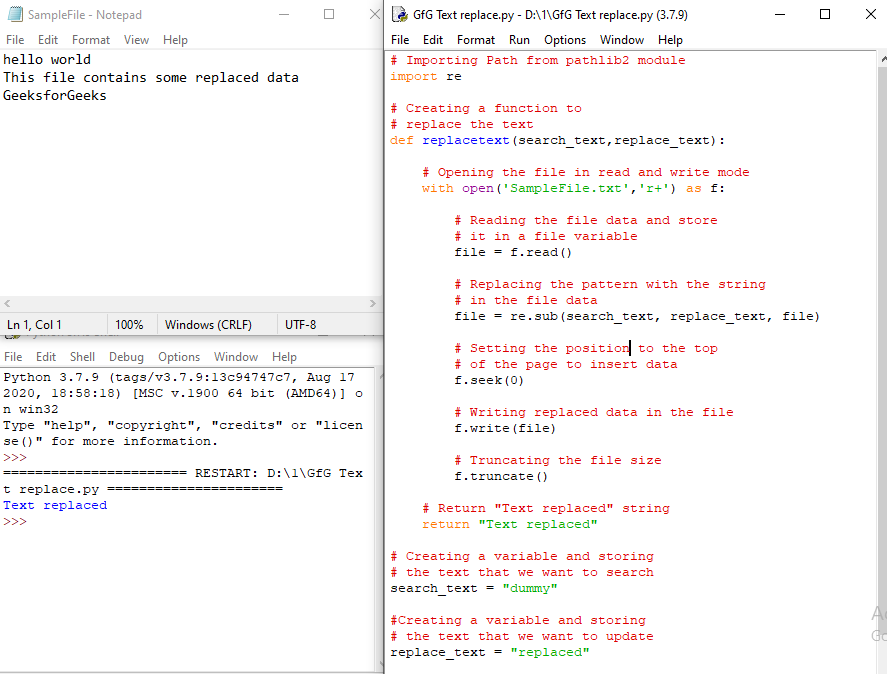
Code:
Python3
import re
def replacetext(search_text,replace_text):
with open('SampleFile.txt','r+') as f:
file = f.read()
file = re.sub(search_text, replace_text, file)
f.seek(0)
f.write(file)
f.truncate()
return "Text replaced"
search_text = "dummy"
replace_text = "replaced"
print(replacetext(search_text,replace_text))
Output:
Text replaced
Method 4: Using fileinput
Let see how we can search and replace text using the fileinput module. For this, we will use FileInput() method to iterate over the data of the file and replace the text.
Syntax: FileInput(files=None, inplace=False, backup=”, *, mode=’r’)
Parameters:
- files : Location of the text file
- mode : Mode in which you want toopen the file
- inplace : If value is True then the file is moved to a backup file and
- standard output is directed to the input file
- backup : Extension for the backup file
Code:
Python3
from fileinput import FileInput
def replacetext(search_text, replace_text):
with FileInput("SampleFile.txt", inplace=True,
backup='.bak') as f:
for line in f:
print(line.replace(search_text,
replace_text), end='')
return "Text replaced"
search_text = "dummy"
replace_text = "replaced"
print(replacetext(search_text, replace_text))
Output:
Text replaced
Last Updated :
14 Sep, 2021
Like Article
Save Article
Введение
Поиск информации, хранящейся в различных структурах данных, является важной частью практически каждого приложения.
Существует множество различных алгоритмов, которые можно использовать для поиска. Каждый из них имеет разные реализации и напрямую зависит от структуры данных, для которой он реализован.
Умение выбрать нужный алгоритм для конкретной задачи является ключевым навыком для разработчиков. Именно правильно подобранный алгоритм отличает быстрое, надежное и стабильное приложение от приложения, которое падает от простого запроса.
В этой статье:
- Операторы членства (Membership Operators)
- Линейный поиск
- Бинарный поиск
- Улучшенный линейный поиск — Jump Search
- Поиск Фибоначчи
- Экспоненциальный поиск
- Интерполяционный поиск
Операторы членства (Membership Operators)
Алгоритмы развиваются и оптимизируются в результате постоянной эволюции и необходимости находить наиболее эффективные решения для основных проблем в различных областях.
Одной из наиболее распространенных проблем в области компьютерных наук является поиск в коллекции и определение того, присутствует ли данный объект в коллекции или нет.
Почти каждый язык программирования имеет свою собственную реализацию базового алгоритма поиска. Обычно — в виде функции, которая возвращает логическое значение True или False, когда элемент найден в данной коллекции элементов.
В Python самый простой способ поиска объекта — использовать операторы членства. Их название связано с тем, что они позволяют нам определить, является ли данный объект членом коллекции.
Эти операторы могут использоваться с любой итерируемой структурой данных в Python, включая строки, списки и кортежи.
in— возвращаетTrue, если данный элемент присутствует в структуре данных.not in— возвращаетTrue, если данный элемент не присутствует в структуре данных.
>>> 'apple' in ['orange', 'apple', 'grape'] True >>> 't' in 'pythonist' True >>> 'q' in 'pythonist' False >>> 'q' not in 'pythonist' True
Операторов членства достаточно, если нам нужно только определить, существует ли подстрока в данной строке, или пересекаются ли две строки, два списка или кортежа с точки зрения содержащихся в них объектов.
В большинстве случаев помимо определения, наличествует ли элемент в последовательности, нам нужна еще и позиция (индекс) элемента. Используя операторы членства, мы не можем получить ее.
Существует множество алгоритмов поиска, которые не зависят от встроенных операторов и могут использоваться для более быстрого и/или эффективного поиска значений. Кроме того, они могут дать больше информации (например, о позиции элемента в коллекции), а не просто определить, есть ли в коллекции этот элемент.
Линейный поиск
Линейный поиск — это один из самых простых и понятных алгоритмов поиска. Мы можем думать о нем как о расширенной версии нашей собственной реализации оператора in в Python.
Суть алгоритма заключается в том, чтобы перебрать массив и вернуть индекс первого вхождения элемента, когда он найден:
def LinearSearch(lys, element):
for i in range (len(lys)):
if lys[i] == element:
return i
return -1
Итак, если мы используем функцию для вычисления:
>>> print(LinearSearch([1,2,3,4,5,2,1], 2))
То получим следующий результат:
1
Это индекс первого вхождения искомого элемента, учитывая, что нумерация элементов в Python начинается с нуля.
Временная сложность линейного поиска равна O(n). Это означает, что время, необходимое для выполнения, увеличивается с увеличением количества элементов в нашем входном списке lys.
Линейный поиск не часто используется на практике, потому что такая же эффективность может быть достигнута с помощью встроенных методов или существующих операторов. К тому же, он не такой быстрый и эффективный, как другие алгоритмы поиска.
Линейный поиск хорошо подходит для тех случаев, когда нам нужно найти первое вхождение элемента в несортированной коллекции. Это связано с тем, что он не требует сортировки коллекции перед поиском (в отличие от большинства других алгоритмов поиска).
Бинарный поиск
Бинарный поиск работает по принципу «разделяй и властвуй». Он быстрее, чем линейный поиск, но требует, чтобы массив был отсортирован перед выполнением алгоритма.
Предполагая, что мы ищем значение val в отсортированном массиве, алгоритм сравнивает val со значением среднего элемента массива, который мы будем называть mid.
- Если
mid— это тот элемент, который мы ищем (в лучшем случае), мы возвращаем его индекс. - Если нет, мы определяем, в какой половине массива мы будем искать
valдальше, основываясь на том, меньше или больше значениеvalзначенияmid, и отбрасываем вторую половину массива. - Затем мы рекурсивно или итеративно выполняем те же шаги, выбирая новое значение для
mid, сравнивая его сvalи отбрасывая половину массива на каждой итерации алгоритма.
Алгоритм бинарного поиска можно написать как рекурсивно, так и итеративно. В Python рекурсия обычно медленнее, потому что она требует выделения новых кадров стека.
Поскольку хороший алгоритм поиска должен быть максимально быстрым и точным, давайте рассмотрим итеративную реализацию бинарного поиска:
def BinarySearch(lys, val):
first = 0
last = len(lys)-1
index = -1
while (first <= last) and (index == -1):
mid = (first+last)//2
if lys[mid] == val:
index = mid
else:
if val<lys[mid]:
last = mid -1
else:
first = mid +1
return index
Если мы используем функцию для вычисления:
>>> BinarySearch([10,20,30,40,50], 20)
То получим следующий результат, являющийся индексом искомого значения:
1
На каждой итерации алгоритм выполняет одно из следующих действий:
- Возврат индекса текущего элемента.
- Поиск в левой половине массива.
- Поиск в правой половине массива.
Мы можем выбрать только одно действие на каждой итерации. Также на каждой итерации наш массив делится на две части. Из-за этого временная сложность двоичного поиска равна O(log n).
Одним из недостатков бинарного поиска является то, что если в массиве имеется несколько вхождений элемента, он возвращает индекс не первого элемента, а ближайшего к середине:
>>> print(BinarySearch([4,4,4,4,4], 4))
После выполнения этого фрагмента кода будет возвращен индекс среднего элемента:
2
Для сравнения: выполнение линейного поиска по тому же массиву вернет индекс первого элемента:
0
Однако мы не можем категорически утверждать, что двоичный поиск не работает, если массив содержит дубликаты. Он может работать так же, как линейный поиск, и в некоторых случаях возвращать первое вхождение элемента. Например:
>>> print(BinarySearch([1,2,3,4,4,4,5], 4)) 3
Бинарный поиск довольно часто используется на практике, потому что он эффективен и быстр по сравнению с линейным поиском. Однако у него есть некоторые недостатки, такие как зависимость от оператора //. Существует много других алгоритмов поиска, работающих по принципу «разделяй и властвуй», которые являются производными от бинарного поиска. Некоторые из них мы рассмотрим далее.
Jump Search
Jump Search похож на бинарный поиск тем, что он также работает с отсортированным массивом и использует аналогичный подход «разделяй и властвуй» для поиска по нему.
Его можно классифицировать как усовершенствованный алгоритм линейного поиска, поскольку он зависит от линейного поиска для выполнения фактического сравнения при поиске значения.
В заданном отсортированном массиве мы ищем не постепенно по элементам массива, а скачкообразно. Если у нас есть размер прыжка, то наш алгоритм будет рассматривать элементы входного списка lys в следующем порядке: lys[0], lys[0+jump], lys[0+2jump], lys[0+3jump] и так далее.
С каждым прыжком мы сохраняем предыдущее значение и его индекс. Когда мы находим множество значений (блок), где lys[i] < element < lys[i + jump], мы выполняем линейный поиск с lys[i] в качестве самого левого элемента и lys[i + jump] в качестве самого правого элемента в нашем множестве:
import math
def JumpSearch (lys, val):
length = len(lys)
jump = int(math.sqrt(length))
left, right = 0, 0
while left < length and lys[left] <= val:
right = min(length - 1, left + jump)
if lys[left] <= val and lys[right] >= val:
break
left += jump;
if left >= length or lys[left] > val:
return -1
right = min(length - 1, right)
i = left
while i <= right and lys[i] <= val:
if lys[i] == val:
return i
i += 1
return -1
Поскольку это сложный алгоритм, давайте рассмотрим пошаговое вычисление для следующего примера:
>>> print(JumpSearch([1,2,3,4,5,6,7,8,9], 5))
- Jump search сначала определит размер прыжка путем вычисления
math.sqrt(len(lys)). Поскольку у нас 9 элементов, размер прыжка будет √9 = 3. - Далее мы вычисляем значение переменной
right. Оно рассчитывается как минимум из двух значений: длины массива минус 1 и значенияleft + jump, которое в нашем случае будет 0 + 3 = 3. Поскольку 3 меньше 8, мы используем 3 в качестве значения переменнойright. - Теперь проверим, находится ли наш искомый элемент 5 между
lys[0]иlys[3]. Поскольку 5 не находится между 1 и 4, мы идем дальше. - Затем мы снова делаем расчеты и проверяем, находится ли наш искомый элемент между
lys[3]иlys[6], где 6 — это 3 + jump. Поскольку 5 находится между 4 и 7, мы выполняем линейный поиск по элементам междуlys[3]иlys[6]и возвращаем индекс нашего элемента:
4
Временная сложность jump search равна O(√n), где √n — размер прыжка, а n — длина списка. Таким образом, с точки зрения эффективности jump search находится между алгоритмами линейного и бинарного поиска.
Единственное наиболее важное преимущество jump search по сравнению с бинарным поиском заключается в том, что он не опирается на оператор деления (/).
В большинстве процессоров использование оператора деления является дорогостоящим по сравнению с другими основными арифметическими операциями (сложение, вычитание и умножение), поскольку реализация алгоритма деления является итеративной.
Стоимость сама по себе очень мала, но когда количество искомых элементов очень велико, а количество необходимых операций деления растет, стоимость может постепенно увеличиваться. Поэтому jump search лучше бинарного поиска, когда в системе имеется большое количество элементов: там даже небольшое увеличение скорости имеет значение.
Чтобы ускорить jump search, мы могли бы использовать бинарный поиск или какой-нибудь другой алгоритм для поиска в блоке вместо использования гораздо более медленного линейного поиска.
Поиск Фибоначчи
Поиск Фибоначчи — это еще один алгоритм «разделяй и властвуй», который имеет сходство как с бинарным поиском, так и с jump search. Он получил свое название потому, что использует числа Фибоначчи для вычисления размера блока или диапазона поиска на каждом шаге.
Числа Фибоначчи — это последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21 …, где каждый элемент является суммой двух предыдущих чисел.
Алгоритм работает с тремя числами Фибоначчи одновременно. Давайте назовем эти три числа fibM, fibM_minus_1 и fibM_minus_2. Где fibM_minus_1 и fibM_minus_2 — это два числа, предшествующих fibM в последовательности:
fibM = fibM_minus_1 + fibM_minus_2
Мы инициализируем значения 0, 1, 1 или первые три числа в последовательности Фибоначчи. Это поможет нам избежать IndexError в случае, когда наш массив lys содержит очень маленькое количество элементов.
Затем мы выбираем наименьшее число последовательности Фибоначчи, которое больше или равно числу элементов в нашем массиве lys, в качестве значения fibM. А два числа Фибоначчи непосредственно перед ним — в качестве значений fibM_minus_1 и fibM_minus_2. Пока в массиве есть элементы и значение fibM больше единицы, мы:
- Сравниваем
valсо значением блока в диапазоне доfibM_minus_2и возвращаем индекс элемента, если он совпадает. - Если значение больше, чем элемент, который мы в данный момент просматриваем, мы перемещаем значения
fibM,fibM_minus_1иfibM_minus_2на два шага вниз в последовательности Фибоначчи и меняем индекс на индекс элемента. - Если значение меньше, чем элемент, который мы в данный момент просматриваем, мы перемещаем значения
fibM,fibM_minus_1иfibM_minus_2на один шаг вниз в последовательности Фибоначчи.
Давайте посмотрим на реализацию этого алгоритма на Python:
def FibonacciSearch(lys, val):
fibM_minus_2 = 0
fibM_minus_1 = 1
fibM = fibM_minus_1 + fibM_minus_2
while (fibM < len(lys)):
fibM_minus_2 = fibM_minus_1
fibM_minus_1 = fibM
fibM = fibM_minus_1 + fibM_minus_2
index = -1;
while (fibM > 1):
i = min(index + fibM_minus_2, (len(lys)-1))
if (lys[i] < val):
fibM = fibM_minus_1
fibM_minus_1 = fibM_minus_2
fibM_minus_2 = fibM - fibM_minus_1
index = i
elif (lys[i] > val):
fibM = fibM_minus_2
fibM_minus_1 = fibM_minus_1 - fibM_minus_2
fibM_minus_2 = fibM - fibM_minus_1
else :
return i
if(fibM_minus_1 and index < (len(lys)-1) and lys[index+1] == val):
return index+1;
return -1
Используем функцию FibonacciSearch для вычисления:
>>> print(FibonacciSearch([1,2,3,4,5,6,7,8,9,10,11], 6))
Давайте посмотрим на пошаговый процесс поиска:
- Присваиваем переменной
fibMнаименьшее число Фибоначчи, которое больше или равно длине списка. В данном случае наименьшее число Фибоначчи, отвечающее нашим требованиям, равно 13. - Значения присваиваются следующим образом:
fibM = 13
fibM_minus_1 = 8
fibM_minus_2 = 5
index = -1
- Далее мы проверяем элемент
lys[4], где 4 — это минимум из двух значений —index + fibM_minus_2(-1+5) и длина массива минус 1 (11-1). Поскольку значениеlys[4]равно 5, что меньше искомого значения, мы перемещаем числа Фибоначчи на один шаг вниз в последовательности, получая следующие значения:
fibM = 8
fibM_minus_1 = 5
fibM_minus_2 = 3
index = 4
- Далее мы проверяем элемент
lys[7], где 7 — это минимум из двух значений:index + fibM_minus_2(4 + 3) и длина массива минус 1 (11-1). Поскольку значениеlys[7]равно 8, что больше искомого значения, мы перемещаем числа Фибоначчи на два шага вниз в последовательности, получая следующие значения:
fibM = 3
fibM_minus_1 = 2
fibM_minus_2 = 1
index = 4
- Затем мы проверяем элемент
lys[5], где 5 — это минимум из двух значений:index + fibM_minus_2(4+1) и длина массива минус 1 (11-1) . Значениеlys[5]равно 6, и это наше искомое значение!
Получаем ожидаемый результат:
5
Временная сложность поиска Фибоначчи равна O(log n). Она такая же, как и у бинарного поиска. Это означает, что алгоритм в большинстве случаев работает быстрее, чем линейный поиск и jump search.
Поиск Фибоначчи можно использовать, когда у нас очень большое количество искомых элементов и мы хотим уменьшить неэффективность, связанную с использованием алгоритма, основанного на операторе деления.
Дополнительным преимуществом использования поиска Фибоначчи является то, что он может вместить входные массивы, которые слишком велики для хранения в кэше процессора или ОЗУ, потому что он ищет элементы с увеличивающимся шагом, а не с фиксированным.
Экспоненциальный поиск
Экспоненциальный поиск — это еще один алгоритм поиска, который может быть достаточно легко реализован на Python, по сравнению с jump search и поиском Фибоначчи, которые немного сложны. Он также известен под названиями galloping search, doubling search и Struzik search.
Экспоненциальный поиск зависит от бинарного поиска для выполнения окончательного сравнения значений. Алгоритм работает следующим образом:
- Определяется диапазон, в котором, скорее всего, будет находиться искомый элемент.
- В этом диапазоне используется двоичный поиск для нахождения индекса элемента.
Реализация алгоритма экспоненциального поиска на Python:
def ExponentialSearch(lys, val):
if lys[0] == val:
return 0
index = 1
while index < len(lys) and lys[index] <= val:
index = index * 2
return BinarySearch( lys[:min(index, len(lys))], val)
Используем функцию, чтобы найти значение:
>>> print(ExponentialSearch([1,2,3,4,5,6,7,8],3))
Рассмотрим работу алгоритма пошагово.
- Проверяем, соответствует ли первый элемент списка искомому значению: поскольку
lys[0]равен 1, а мы ищем 3, мы устанавливаем индекс равным 1 и двигаемся дальше. - Перебираем все элементы в списке, и пока элемент с текущим индексом меньше или равен нашему значению, умножаем значение индекса на 2:
- index = 1,
lys[1]равно 2, что меньше 3, поэтому значение index умножается на 2 и переменнойindexприсваивается значение 2. - index = 2,
lys[2]равно 3, что равно 3, поэтому значениеindexумножается на 2 и переменнойindexприсваивается значение 4. - index = 4,
lys[4]равно 5, что больше 3. Условие выполнения цикла больше не соблюдается и цикл завершает свою работу.
- Затем выполняется двоичный поиск в полученном диапазоне (срезе)
lys[:4]. В Python это означает, что подсписок будет содержать все элементы до 4-го элемента, поэтому мы фактически вызываем функцию следующим образом:
>>> BinarySearch([1,2,3,4], 3)
Функция вернет следующий результат:
2
Этот результат является индексом искомого элемента как в исходном списке, так и в срезе, который мы передаем алгоритму бинарного поиска.
Экспоненциальный поиск выполняется за время O(log i), где i — индекс искомого элемента. В худшем случае временная сложность равна O(log n), когда искомый элемент — это последний элемент в массиве (n — это длина массива).
Экспоненциальный поиск работает лучше, чем бинарный, когда искомый элемент находится ближе к началу массива. На практике мы используем экспоненциальный поиск, поскольку это один из наиболее эффективных алгоритмов поиска в неограниченных или бесконечных массивах.
Интерполяционный поиск
Интерполяционный поиск — это еще один алгоритм «разделяй и властвуй», аналогичный бинарному поиску. В отличие от бинарного поиска, он не всегда начинает поиск с середины. Интерполяционный поиск вычисляет вероятную позицию искомого элемента по формуле:
index = low + [(val-lys[low])*(high-low) / (lys[high]-lys[low])]
В этой формуле используются следующие переменные:
- lys — наш входной массив.
- val — искомый элемент.
- index — вероятный индекс искомого элемента. Он вычисляется как более высокое значение, когда значение val ближе по значению к элементу в конце массива (
lys[high]), и более низкое, когда значение val ближе по значению к элементу в начале массива (lys[low]). - low — начальный индекс массива.
- high — последний индекс массива.
Алгоритм осуществляет поиск путем вычисления значения индекса:
- Если значение найдено (когда
lys[index] == val), возвращается индекс. - Если значение
valменьшеlys[index], то значение индекса пересчитывается по формуле для левого подмассива. - Если значение
valбольшеlys[index], то значение индекса пересчитывается по формуле для правого подмассива.
Давайте посмотрим на реализацию интерполяционного поиска на Python:
def InterpolationSearch(lys, val):
low = 0
high = (len(lys) - 1)
while low <= high and val >= lys[low] and val <= lys[high]:
index = low + int(((float(high - low) / ( lys[high] - lys[low])) * ( val - lys[low])))
if lys[index] == val:
return index
if lys[index] < val:
low = index + 1;
else:
high = index - 1;
return -1
Если мы используем функцию для вычисления:
>>> print(InterpolationSearch([1,2,3,4,5,6,7,8], 6))
Наши начальные значения будут следующими:
val = 6,
low = 0,
high = 7,
lys[low] = 1,
lys[high] = 8,
index = 0 + [(6-1)*(7-0)/(8-1)] = 5
Поскольку lys[5] равно 6, что является искомым значением, мы прекращаем выполнение и возвращаем результат:
5
Если у нас большое количество элементов и наш индекс не может быть вычислен за одну итерацию, то мы продолжаем пересчитывать значение индекса после корректировки значений high и low.
Временная сложность интерполяционного поиска равна O(log log n), когда значения распределены равномерно. Если значения распределены неравномерно, временная сложность для наихудшего случая равна O(n) — так же, как и для линейного поиска.
Интерполяционный поиск лучше всего работает на равномерно распределенных, отсортированных массивах. В то время как бинарный поиск начинает поиск с середины и всегда делит массив на две части, интерполяционный поиск вычисляет вероятную позицию элемента и проверяет индекс, что повышает вероятность нахождения элемента за меньшее количество итераций.
Python очень удобочитаемый и эффективный по сравнению с такими языками программирования, как Java, Fortran, C, C++ и т. д. Одним из ключевых преимуществ использования Python для реализации алгоритмов поиска является то, что вам не нужно беспокоиться о приведении или явной типизации.
В Python большинство алгоритмов поиска, которые мы обсуждали, будут работать так же хорошо, если мы ищем строку. Имейте в виду, что понадобится внести изменения в код для алгоритмов, которые используют искомый элемент для числовых вычислений, например алгоритм интерполяционного поиска.
Python также подходит, если вы хотите сравнить производительность различных алгоритмов поиска для вашего dataset’а. Создание прототипа на Python проще и быстрее, потому что вы можете сделать больше с меньшим количеством строк кода.
Чтобы сравнить производительность наших реализованных алгоритмов, в Python мы можем использовать библиотеку time:
import time start = time.time() # вызовите здесь функцию end = time.time() print(start-end)
Заключение
Существует множество возможных способов поиска элемента в коллекции. В этой статье мы обсудили несколько алгоритмов поиска и их реализации на Python.
Выбор используемого алгоритма зависит от данных, с которыми вы будете работать. Это ваш входной массив, который мы называли lys во всех наших реализациях.
- Если вы хотите выполнить поиск в несортированном массиве или найти первое вхождение искомой переменной, то лучшим вариантом будет линейный поиск.
- Если вы хотите выполнить поиск в отсортированном массиве, есть много вариантов, из которых самый простой и быстрый — это бинарный поиск.
- Если у вас есть отсортированный массив, в котором вы хотите выполнить поиск без использования оператора деления, вы можете использовать либо jump search, либо поиск Фибоначчи.
- Если вы знаете, что искомый элемент, скорее всего, находится ближе к началу массива, вы можете использовать экспоненциальный поиск.
- Если ваш отсортированный массив равномерно распределен, то самым быстрым и эффективным будет интерполяционный поиск.
Если вы не уверены, какой алгоритм использовать для отсортированного массива, просто протестируйте каждый из них при помощи библиотеки time и выберите тот, который лучше всего работает с вашим dataset’ом.