Как найти объединение множеств на координатной прямой

В результате математических операций над множествами из исходных множеств получается новое множество, причем этот результат однозначен. Примерами таких операций являются пересечение и объединение множеств. Эти операции производятся по определенным правилам, о которых пойдет речь ниже.

Обозначения множеств. Знаки объединения и пересечения множеств

Для обозначения множеств применяется специальная система символов. Самый простой способ описать множество — использование фигурных скобок, внутри которых элементы перечисляются через запятую:

$A = {0, -1, 2, 5, 8, 77}$

Недостатком такой записи является то, что с ее помощью задать множество можно только если оно содержит конечное и не слишком большое количество элементов. Поэтому чаще используется универсальный способ определения множеств — с помощью характеристического свойства, т.е. такого, которое присуще всем его элементам множества, и которым не обладают объекты вне множества:

$A = {x vee P(x)}$,

где $P(x)$ — характеристическое свойство.

В такой форме объединение записывается как

$A cup B = {x | x in A vee x in B}$,

а пересечение как

$A cap B = {x | x in A wedge x in B}$

Знаки $vee$ и $wedge$ обозначают, соответственно, «или» и «и». Знак $|$ читается как «таких, что».

Для обозначения множеств как числовых интервалов используются круглые и квадратные скобки. Например, запись $[4, 24)$ означает, диапазон чисел от $4$ до $24$, причем число $4$ в это множество входит, а $24$ нет, хотя любое число меньше $24$ этому множеству принадлежит.

Для графического выражения операций пересечения и объединения применяются знаки пересечения и объединения множеств:

«Пересечение и объединение множеств» 👇

• $A cup B$ — объединение множеств $A$ и $B$$;;
• $A cap B$ — пересечение множеств $A$ и $B$$..

Для мнемонического запоминания этих знаков можно представить, что знак объединения $cup$ похож на емкость с открытым верхом, куда можно что-то складывать. Знак пересечения $cap$, напротив, представляет собой как бы перевернутый стакан, препятствующий проникновению внутрь неподходящих элементов.

Правила нахождения пересечений и объединений

Правила для нахождения пересечений и объединений множеств заключаются в следующем:

• для составления объединения числовых множеств нужно записать все элементы одного множества и к ним дописать недостающие элементы из остальных;
• для составления пересечения числовых множеств, надо последовательно брать элементы одного множества и проверять, принадлежат ли они другим исследуемым множествам; те, которые принадлежат, и будут составлять пересечение.

Найдем объединение числовых множеств $A = {3, 5, 7, 14}$ и $B = {2, 5, 8, 11, 12, 13}$. К элементам множества $A$ $3, 5, 7, 14$ добавляем недостающие элементы множества $B$ $2, 8, 11, 13$. Результирующее множество будет выглядеть как ${3, 5, 7, 14, 2, 8, 11, 13}$. Это можно записать как

$A ∪ B = {2, 3, 5, 7, 8, 11, 13, 14}$.

Для нахождения пересечения этих же множеств, последовательно проверим элементы $A$ на их наличие внутри $B$. Так, элемент $3$ не принадлежит множеству $B$, значит он не войдет в состав пересечения. Число $5$ из $A$ принадлежит и $B$, а значит и пересечению.Число $7$ не принадлежит $B$ и пересечению, а число 14 принадлежит. Таким образом, пересечение $A = {3, 5, 7, 14}$ и $B = {2, 5, 8, 11, 14, 13}$ состоит из элементов $5$ и $14$. Это записывается как:

$A ∩ B = {5, 14}$.

Пересечение и объединение большего, чем 2 количества множеств сводится к последовательному нахождению пересечений и объединений: чтобы найти пересечение трех множеств $A$, $B$ и $C$ сначала находят пересечение $A$ и $B$, затем пересечение результирующего множества с $C$. Так, пересечение числовых множеств $A = {3, 6, 4, 3, 55, 21}$, $B = {2, 7, 6, 21}$ и $C = {7, 6, 17, 3}$ можно найти поэтапно. Сначала находим, что $A cap B = {6, 21}$, затем полученное множество сравниваем с $C$ (это ${6}$). Получаем, что

$A cap B cap C = {6}$.

Метод нахождения объединений более двух множеств заключается в том, что к числам первого множества добавляют недостающие элементы из второго, затем недостающие из третьего и т.д. Например, если есть $A = {1, 4}$, $B = {4, 3}$ и $C = {1, 3, 6, 7}$, то к числам $1$ и $4$ из $A$ следует добавить число $3$ из $B$, а к полученному множеству ${1, 3, 4}$ нужно добавить $6$ и $7$ из $C$. В результате получаем объединение

$A cup B cup C = {1, 3, 4, 6, 7}$.

Для нахождения пересечения нескольких конечных множеств, нужно перебрать числа первого из них и выяснить, принадлежит ли текущий элемент каждому из рассматриваемых множеств. Если это условие не соблюдается, он не принадлежит пересечению. В качестве проверочного (элементы которого перебираются) следует выбирать множество с наименьшим числом элементов.

Рассмотрим множества $A = {1, 3, 7, 12, 5, 2}$, $B = {0, 1, 2, 12}$, $C = {1, 2, 6, 7, 11}$ и $D = {1, 2, 6, 7, 8, 15}$. Для поиска перебором задействуем $B$ как самое короткое. Элемент множества $B$ $0$ не входит в состав $A$, следовательно, в состав пересечения не войдет. Число $1$ входит в состав $A$, $C$ и $D$. Оно входит в состав их общего пересечения. Число $2$, принадлежащее $B$, входит в состав всех остальных множеств, т.е. входит в состав пересечения. Четвертый элемент проверяемого множества $12$ не входит в состав $D$ и в пересечение не войдет. Таким образом, найденное пересечение выглядит как

$A cap B cap C cap D = {1, 2}$.

Исследование множеств с помощью координатной прямой

Исследовать и выражать пересечения и объединения числовых множеств удобно с помощью координатной прямой и выделяемых на ней числовых промежутков. Любая выбранная точка разбивает все расположенные на такой прямой числа на два открытых числовых луча. Например, точка с координатой $36,6$ создаст промежутки, записываемые как $(−∞, 36,6)$, $(36,6, +∞)$. Сама точка не входит в состав ни одного из них, поэтому числовая прямая, представляющая собой множество всех действительных чисел $R = (−∞, +∞)$, представляет собой в данном случае объединение $ (−∞, −36,6) cup {36,6} cup (36,6, +∞)$.

Если рассматриваемую точку со значением $36,6$ добавить к одному из открытых числовых лучей, т.е. промежутку $(−∞, 36,6)$ или $(36,6, +∞)$, то такой промежуток перестанет быть открытым. Это записывается как $(−∞, 36,6]$ или $[36,6, +∞)$, т.е. вхождение граничного числа в состав числового луча обозначается квадратной скобкой. Множество действительных чисел $R$ в этом случае будет выглядеть как

$(−∞, 36,6] cup (36,6, +∞)$ либо $(−∞, 36,6) cup [36,6, +∞)$.

Если разбить числовую прямую на части не точкой, а отрезком или лучом, то все рассмотренные закономерности будут соблюдаться и в этих случаях. Более того, они соблюдаются и при разбиении самих числовых промежутков (отрезков, лучей). Например, точка с координатой $14$ на промежутке $(5, 51]$ разобьет его на промежутки $(5, 14) ∪ {14} ∪ (14, 51]$. Включив точку в один из промежутков, можно получить такие записи, как $(5, 14] cup (14, 51]$, $(5, 14) cup [14, 51]$. Приняв за разбивающую точку число $51$, ограничивающее рассматриваемый промежуток справа и входящее в его состав, получим объединение множества ${51}$ и интервала $(5, 51)$, т.е. $(5, 51] = (5, 51) cup {51}$.

Подобные закономерности справедливы и в случаях, когда координатная прямая разбивается на промежутки несколькими точками. Например, числа $−6$, $0$ и $7$ разобьют ее на промежутки $(−∞, −6)$, $(−6, 0)$, $(0, 7)$, $(7, +∞)$, а множество действительных чисел $R$ будет представлено как $(−∞, −6) ∪ {−6} ∪ (−6, 0) ∪ {0} ∪ (0, 7) ∪ {7} ∪ (7, +∞)$.

С помощью координатной прямой удобно анализировать пересечения и объединения множеств. Они изображаются друг под другом на координатных прямых с совпадающими точками и направлениями отсчета. Для отображения объединения множеств координатные прямые отмечают слева квадратной скобкой, для обозначения пересечения используется фигурная скобка.

На дополнительной координатной прямой, размещаемой под исходными, изображаются искомые пересечение или объединение. На ней все граничные точки исходных множеств отмечают поперечными чертами, а после уточнения — полыми или сплошными точками. Графически вхождение промежутка в пересечение или объединение изображается штриховкой, вхождение точки — сплошной точкой, невхождение – полой.

Пересечение множеств $A$ и $B$ графически отображается промежутками, над которыми есть штриховка, с добавлением отдельных точек, принадлежащих обоим множествам. Объединение графически проявляется там, где есть штриховка хотя бы у одного из множеств, а также всех сплошных точек.

Решение некоторых математических задач предусматривает операции над множествами такие как пересечение, объединение, разность. Под множеством подразумевают объединение некоторых предметов в одно целое. Для совершения подобных действий требуется знание некоторых правил, которые позволят найти пересечение, объединение и разность множеств. О таких правилах пойдёт речь далее.

Обозначение множеств. Как записать объединение и пересечение множеств

При записи обозначения пересечения множеств и объединения множества чисел, используют специальный порядок символов. Самый лёгкий способ обозначить множество — это применение фигурных скобок, в середине которых элементы записаны через запятую.

А = {7, 3, 15, 31}

С помощью такой записи можно задать множество, если оно включает небольшое конечное число элементов. В связи с этим чаще применяется многофункциональный способ определения множеств – посредством характеристического свойства, которое свойственно всем элементам множества, которым не владеют объекты вне множества.

A = {x | P(x)} или A = {x : P(x)}

P(x) – характеристическое свойство множества A.

В таком виде объединение записывается следующим образом:

AUB={x|xєAvxєB}

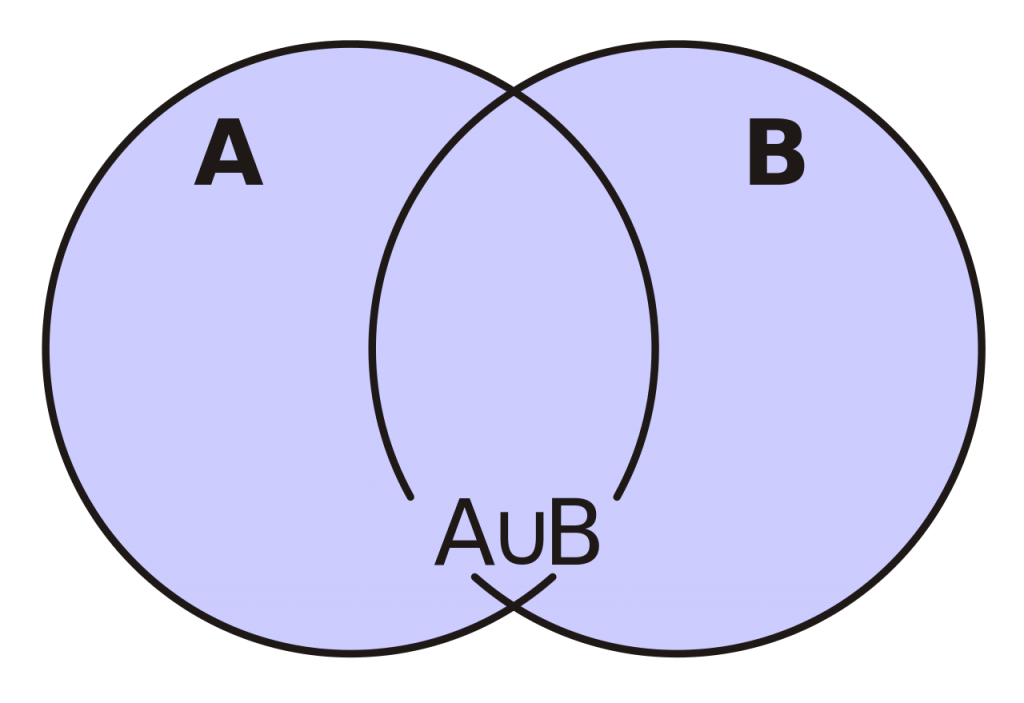
а пересечение множеств записывается как:

AՈB={x|xєAᴧxєB}

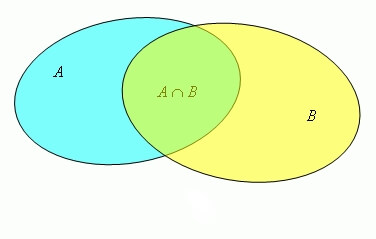
Где символы v / ᴧ, обозначают «или» / «и», символ | обозначает «таких что».

Чтобы обозначить множества, как числовые интервалы, при записи применяют скобки круглой и квадратной формы. К примеру, запись [4,24), выражает цифровой диапазон от 4 до 24, при этом число 4 входит в состав множества, а 24 нет. Числа менее 24 принадлежат этому множеству.

Найти пересечение и объединение множеств. Операции над множествами

Чтобы легче запомнить данные знаки пересечения и объединения множеств, можно мысленно представить, что символ объединения U напоминает сосуд с открытым верхом, туда есть возможность что-то положить.

Символ пересечения Ո наоборот, выглядит как перевёрнутая ёмкость, в который невозможно поместить какой-либо предмет. Так же символ обозначающий пересечение Ո можно прочитать как «И».

Тогда выражение AՈB=C, читается так: “Все элементы, входящие в состав множества A и множества B, составляют элементы, которые принадлежат множеству C».

Правила нахождения объединения и пересечения и разности множеств

При формировании объединения числовых множеств, следует последовательно записать полностью части одного множества и их дополнить недостающими элементами из остальных. Операцию объединения в отдельных случаях называют сложением множеств и обозначают знаком «+».

Рассмотрим пример объединения числовых множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}. К имеющимся числовым составляющим множества A 1,2,3,4,5,6,7,8,9 прибавим недостающую часть из множества B 10. Получившееся в результате объединения множество чисел будет выглядеть так {0,1,2,3,4,5,6,7,8,9,10}. Соответственно запись этого объединения:

AUB={0,1,2,3,4,5,6,7,8,9,10}

Чтобы составить пересечение числовых множеств, следует последовательно выбирать части одного множества и удостовериться, входят ли они в другие исследуемые множества, входящие в их число и составляют пересечение.

Для того, чтобы найти пересечение этих же множеств, друг за другом, последовательно проанализируем числа множества A на их наличие в множестве чисел B. Начнём проверку с самого первого числа в множестве A это число 0. В множестве B данное число отсутствует и не войдёт в совокупность пересечения. Смотрим далее, число 1 из множества A так же имеется в составе множества B. Затем следует число 2, которое принадлежит множеству B и, следовательно, пересечению. Идущее за ним 3 не принадлежит A и B не входит в перечисление. Число 4 входит в A и B, значит войдёт и в объединение. Далее продолжаем проверять числа по аналогии. Итак, пересечение множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10} состоит из чисел 2,4,6,8. При записи выглядит так:

AՈB={2,4,6,8}

Выполнение записи пересечения и объединения нескольких множеств

Если требуется выполнить операции с более чем двумя множествами, например: A, B, C, принцип действия подобный предыдущим примерам. В первую очередь находим пересечения A и B. Только затем пересечение полученного множества с C.

Следовательно, процесс нахождения пересечения более двух множеств осуществляется в несколько этапов.

Например, дано три множества A = {1,2,3,7,9}, B = {1,3,5,7,9} и C = {3,4,5,8,9}. Сначала находим пересечение AՈB = {3,9}, затем сравниваем полученное множество с C, это будут те же 3 и 9. Получаем, что пересечение A, B, C выглядит следующим образом:

AՈBՈC={3,9}

При определении объединений двух и более множеств, к числам первого множества последовательно добавляют отсутствующие элементы из второго, третьего и последующих множеств. К примеру, даны следующее множества A = {1,4}, B = {4,3,} и C = {1,3,6,7}. К числовым элементам 1 и 4 из множества A, прибавляем число 4 из множества B. Теперь, к получившемуся множеству 1,3,4 прибавляем цифры 6 и 7 из множества C. В конечном результате получаем объединение:

AUBUC = {1,3,4,6,7}

Для нахождения пересечения совсем не нужно писать много букв. Когда элементов не много, то множество возможно задать элементарным перечислением. Например, первое множество включает в себя числа 1,3,5, второе состоит из элементов 2,3,5. В данном случае, пересечение будет состоять из элементов 3 и 5. Для записи можно использовать прямое перечисление: {1,3,5} Ո {2,3,5} = {3,5}

Основные свойства объединения и перечисления множеств

1. Коммутативность или перестановка. Распространяется на все компоненты при любом их количестве.
   • AUB = BUA
   • AՈB = BՈA
2. Ассоциативность или расстановка скобок. Позволяет опускать скобки и делать решение проще.
   • (AՈB)ՈC = AՈ(BՈC)
   • (AUB)UC = AU(BUC)
3. Раскрытие скобок или дистрибутивность.
   • (AUB)ՈC=(AՈC)U(BՈC)
   • (AՈB)UC=(AUC)Ո(BUC)

Разностью A и B называется множество, которое включает в себя все элементы, каждое из которых принадлежит множеству A и не принадлежит множеству B. Обозначается AB. Приведём пример, найдём разность множеств A = {1,2,3,4,5} и множества B = {2,4,6,8}. Первый вариант находим разность множества A. Запись будет выглядеть так: AB={1,3,5}, в которую не входят элементы, принадлежащие только B числа 6 и 8. Разность множества B при этом выглядит так: BA={6,8}, сюда соответственно не входят числа, принадлежащие только A.

Для закрепления материала пройденных уроков, рассмотрим ещё несколько примеров. Дана задача: A = {0,5,8,10}, B = {3,6,8,9} и X = {0,1,3} Y = {2,4,6}. Найдите пересечение, объединение для A, B и разность множеств X, Y. Решение:

Сначала найдём объединение исходных множеств A U B = {0,3,5,6,8,9,10}.

Затем пересечение A Ո B = {8}

Разность XY = {0,1,3} YX = {2,4,6}

Для того, чтобы выполнить операции над множествами пересечения, объединения, разность в количестве больше двух, следует рассматривать элементы, входящие в первое их них. Затем определить, относится ли этот элемент к каждому из проверяемых множеств. Если данное обстоятельство не соблюдено, то элемент не относится к пересечению. При проверке, лучше выбирать множество с наименьшим количеством элементов в составе.

Кроме перечисленных действий пересечения и объедения существует дополнение множеств и многие другие операции.

Отображение множеств с помощью координатной прямой

Для того, чтобы исследовать и обозначать множества, удобно применять выделение числовых промежутков на координатной прямой. Каждая выбранная точка разделяет находящиеся на ней числа на два открытых луча. Приведём пример, точка с координатами 42,7 сформирует промежутки, которые можно записать как (-∞,42,7) и (42,7, +∞). Наше выражение заключено в круглые скобки, это значит, что сама точка 42,7 ни одному из этих промежутков не принадлежит. Числовая прямая, которая записывается как R = (-∞,+∞), при таком варианте из нашего примера, представляет объединение:

(-∞,42,7) U {42,7} U (42,7+∞).

При добавлении нашей рассматриваемой точки 42,7 к одному из представленных (-∞,42,7) или (42,7, +∞) числовых лучей, в таком случае промежуток перестанет быть открытым. При записи выражения нужно будет использовать квадратные скобки, которые обозначают, что точка входит в промежуток. Запись будет выглядеть так: (-∞,42,7] и [42,7+∞). Тем самым множество действительных чисел на координатной прямой будет выглядеть так:

(-∞,42,7] U (42,7+∞) или (-∞,42,7) U [42,7+∞).

На числовой прямой можно выполнять большое количество действий. Такую прямую можно разделить на отрезки не точкой, как в предыдущем примере, а лучом или отрезком. Все выявленные закономерности так же будут соблюдены. Кроме того, они выполняются при разделении самих числовых промежутков. Рассмотрим пример, точка с координатой 18 на промежутке (8,34] разделит его на следующие промежутки (8,18) U {18} U (18,34]. Дополнив точкой, один из промежутков, получатся следующее записи: (8,18] U (18,34], (8,18) U [18,34]. Примем за разделяющую точку цифру 34, которая включается в состав рассматриваемого промежутка и ограничивает его справа. В результате получим объединение множеств {34} и интервала (8,34) либо (8,34] = (8,34) U {34}

Аналогичные закономерности объективны и в ситуации, когда координатная прямая разделяется на промежутки несколькими точками. К примеру, точки -5, 0 и 6 разделят её на промежутки (-∞,-5), (-5,0), (0,6), (6,+∞), при этом множество действительных чисел (-∞,-5) U {-5} U (-5,0) U {0} U (0,6) U {6} U (6,+∞).

Благодаря координатной прямой достаточно просто и легко рассматривать пересечения и объединения множеств. Они указываются друг под другом на координатных прямых с идентичными направлениями отсчёта и точками. При записи отображения множеств координатные прямые обозначают слева квадратной скобкой, фигурные скобки используются, чтобы показать пересечение.

С помощью дополнительной координатной прямой, которую располагают ниже исходной, показываются искомые пересечения или объединение. На ней поперечными чертами отмечают граничные точки первичных множеств, а после выяснения характера точек, их заменяют полями или сплошными. На рисунке вхождение промежутка в объединение показывается штриховкой, отсутствие вхождения – полой точкой, а вхождение – сплошной.

Графически пересечение A и B показывается промежутками, над которыми имеется штриховка, дополненная отдельными точками, которые принадлежат обоим множествам. На рисунке объединение проявляется там, где показана штриховка хотя бы у одного из множеств и сплошные точки.

В приведённых примерах объединения и пересечения множеств указаны только целые числа. Отрезкам на координатной прямой так же принадлежат и другие числа, которые целыми не являются, такие как десятичные дроби. При определении пересечения и определения множеств, класс чисел намного шире, чем представлен в упражнениях, они находятся между целыми числами и количество их очень велико, перечислять которые не представляется возможным.

Теория множеств

Говоря простым языком, множество — это элементарный математический объект, который содержит определенный набор данных, предметов или чисел. Это исходное математическое понятие, которое невозможно представить другими терминами. Именно поэтому множество описывается как набор разрозненных элементов, мыслимое как единое целое. Понятие множества ввел немецкий математик Георг Кантор, который развил собственную теорию трансфинитных чисел, позволяющую оперировать вполне упорядоченными бесконечными множествами.

Георг Кантор разработал уникальную программу стандартизации всех математических знаний, согласно которой любой математический объект является тем или иным множеством. К примеру, согласно канторовской теории, любое натуральное число — это одноэлементное множество, принадлежащее надмножеству натурального ряда. Натуральный ряд, в свою очередь, считается подмножеством целого ряда, а целое множество — подмножеством действительного или вещественного ряда.

Теория Георга Кантора вызвала широкий резонанс в математических кругах. Многие современники негативно отзывались о его работах, особенно его учитель Леопольд Кронекер, который не принимал канторовского определения натурального числа. Несмотря на это, теория множеств получила признание позже, когда группа французских математиков под псевдонимом Никола Бурбаки предприняла попытку перевести весь математический аппарат на теоретико-множественный язык.

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример:

А = {а, в, с, у} – А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

• конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
• бесконечные — не являющиеся конечными (например, числовые);
• пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.

Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.

N = {9, 11, 13, 15……}.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Z = {-112, -60, -25, 0, 36, 58, 256}.

Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Объединение

Пересечение множеств

Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:

$$ A cap B = {x|x in Bbb A и x in Bbb B } $$

Если множества не пересекаются, то $A cap B = varnothing $ — пустое множество в пересечении. Если $B subseteq A$ — подмножество, то $A cap B = B$ – пересечением будет меньшее множество из двух.

Например:

Если A = {1;3;5;9}, Β = {3;7;11}, то $A cap B$ = {3;5}.

Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A cap B$ = {f|f-квадрат}.

Если A = ${n|n⋮3, n in Bbb N }$ — натуральные числа, кратные 3, B = ${n|n⋮5, n in Bbb N }$ — натуральные числа, кратные 5, то $A cap B = {n|n⋮15, n in Bbb N}$ — натуральные числа, кратные 15.

Если A = {a│a-слон}, B = {a|a-птица}, то $A cap B = varnothing$.

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Универсум и отрицание

Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.

В литературе универсум обозначают U.

На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:

Примеры универсумов:

1. При рассмотрении целочисленных задач, универсум – это множество целых чисел.
2. При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
3. При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.

Отрицание (абсолютное дополнение) множества A — множество всех элементов универсума, не принадлежащих A:

$$ bar{A} = {x|x notin A } $$

Читается «не A».

У отрицания есть любопытное свойство: $bar{bar{Α}} = Α $(два раза «нет» — это «да»).

Например:

Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $bar{A} = {1;2;6;7}$

Если U = ${x|x in Bbb R}$ — все действительные числа, A = ${x|x gt 0, x in Bbb R }$ — все положительные действительные числа, то $ bar{A} = {x|x le 0, x in Bbb R}$.

Разность множеств

Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:

$$ AB = {x|x in Bbb A , x notin B} $$

Читается «A без B».

На диаграммах Эйлера разности для пересекающихся множеств выглядят так:

Получается, что отрицание – частный случай разности: $ bar{A} = {x|x in Bbb U, x notin A } $= UA

«Не A» — это «универсум без A».

Формулы включений и исключений

Рассмотрим два конечных пересекающихся множества A и B.

Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A cap B)$.

Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A cup B)$?

Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:

$$n(A cup B) = n(A)+ n(B)-n(A cap B)$$

Выведем аналогичную формулу для трёх пересекающихся конечных множеств.

Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A cap B)+n(A cap C)+n(B cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A cap B cap C)$; значит, его нужно «вернуть».

Получаем:

$$ n(A cup B cup C) = n(A)+ n(B)+n(C)- $$

$$ -(n(A cap B)+n(A cap C)+n(B cap C) )+n(A cap B cap C) $$

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

• умножения S ∩ D = D ∩ S;
• сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

• умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
• сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

• умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
• умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
• сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

Транзитивность — законы включения:

• если S ⊆ Fи F ⊆ J, то S ⊆ J;
• если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

• S ∩ S = S;
• S ∪ S = S.

О других свойствах операций можно узнать из картинки:

Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.

Исследование множеств с помощью координатной прямой

Исследовать и выражать пересечения и объединения числовых множеств удобно с помощью координатной прямой и выделяемых на ней числовых промежутков. Любая выбранная точка разбивает все расположенные на такой прямой числа на два открытых числовых луча. Например, точка с координатой $36,6$ создаст промежутки, записываемые как $(−∞, 36,6)$, $(36,6, +∞)$. Сама точка не входит в состав ни одного из них, поэтому числовая прямая, представляющая собой множество всех действительных чисел $R = (−∞, +∞)$, представляет собой в данном случае объединение $ (−∞, −36,6) cup {36,6} cup (36,6, +∞)$.

Если рассматриваемую точку со значением $36,6$ добавить к одному из открытых числовых лучей, т.е. промежутку $(−∞, 36,6)$ или $(36,6, +∞)$, то такой промежуток перестанет быть открытым. Это записывается как $(−∞, 36,6]$ или $[36,6, +∞)$, т.е. вхождение граничного числа в состав числового луча обозначается квадратной скобкой. Множество действительных чисел $R$ в этом случае будет выглядеть как

$(−∞, 36,6] cup (36,6, +∞)$ либо $(−∞, 36,6) cup [36,6, +∞)$.

Если разбить числовую прямую на части не точкой, а отрезком или лучом, то все рассмотренные закономерности будут соблюдаться и в этих случаях. Более того, они соблюдаются и при разбиении самих числовых промежутков (отрезков, лучей).

Например, точка с координатой $14$ на промежутке $(5, 51]$ разобьет его на промежутки $(5, 14) ∪ {14} ∪ (14, 51]$. Включив точку в один из промежутков, можно получить такие записи, как $(5, 14] cup (14, 51]$, $(5, 14) cup [14, 51]$. Приняв за разбивающую точку число $51$, ограничивающее рассматриваемый промежуток справа и входящее в его состав, получим объединение множества ${51}$ и интервала $(5, 51)$, т.е. $(5, 51] = (5, 51) cup {51}$.

Подобные закономерности справедливы и в случаях, когда координатная прямая разбивается на промежутки несколькими точками. Например, числа $−6$, $0$ и $7$ разобьют ее на промежутки $(−∞, −6)$, $(−6, 0)$, $(0, 7)$, $(7, +∞)$, а множество действительных чисел $R$ будет представлено как $(−∞, −6) ∪ {−6} ∪ (−6, 0) ∪ {0} ∪ (0, 7) ∪ {7} ∪ (7, +∞)$.

С помощью координатной прямой удобно анализировать пересечения и объединения множеств. Они изображаются друг под другом на координатных прямых с совпадающими точками и направлениями отсчета. Для отображения объединения множеств координатные прямые отмечают слева квадратной скобкой, для обозначения пересечения используется фигурная скобка.

На дополнительной координатной прямой, размещаемой под исходными, изображаются искомые пересечение или объединение. На ней все граничные точки исходных множеств отмечают поперечными чертами, а после уточнения — полыми или сплошными точками. Графически вхождение промежутка в пересечение или объединение изображается штриховкой, вхождение точки — сплошной точкой, невхождение – полой.

Пересечение множеств $A$ и $B$ графически отображается промежутками, над которыми есть штриховка, с добавлением отдельных точек, принадлежащих обоим множествам. Объединение графически проявляется там, где есть штриховка хотя бы у одного из множеств, а также всех сплошных точек.

Пример 1

Найти пересечение и объединение множеств $A = [-3, 4)$ и $B = [0, 7)$ .

Для решения применим графический метод:

Рисунок 1. Графическое решение задачи. Автор24 — интернет-биржа студенческих работ

Видно, что объединение множеств представляет собой диапазон от крайней левой точки $-3$ включительно до крайней правой $7$ исключая ее. Пересечение множеств начинается от числа $0$. Оно входит в оба множества и ограничивает пересечение слева. Правой границей пересечения является $4$, но оно не входит в первое множество, поэтому здесь граница интервала будет открытой.

Ответ:

$A cap B = [0, 4); A cup B = [-3, 7); $

Примеры из реальной жизни

Геометрические фигуры

Допустим, существует множество X, которое содержит прямоугольники с разными длинами сторон. Также существует множество Y, содержащее ромбы с разными углами. Из курса геометрии мы знаем, что ромб — это параллелограмм, у которого все стороны равны, а прямоугольник — это параллелограмм, у которого равны все углы. В множествах X и Y могут встретиться ромбы с углами по 90 градусов или прямоугольники с одинаковыми сторонами. Фигура, у которой все углы прямые, а все стороны равны — это квадрат. Соответственно, пересечением множеств ромбов X и прямоугольников Y является множество квадратов Z.

Отрезки

Пусть у нас есть два отрезка, которые задаются координатами X = [1, 3] и Y = [2, 4]. Пересечением данных множеств будет отрезок [2, 3], так как именно эти числа входят в диапазон значений обоих отрезков на числовой оси.

Еще пример

Давайте попробуем узнать пересечение пятиэлементных множеств простых и четных чисел. Простое число — это число, которое делится только на себя и на единицу. Четное число — число, которое делится на 2 без остатка. Итак, наши множества S = {2, 3, 5, 7, 11} и E = {2, 4, 6, 8, 10}. Введем эти данные в онлайн-калькулятор и получим результат в виде P = {2}.

Пересечение, объединение и разность множеств