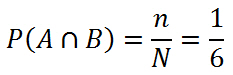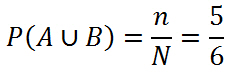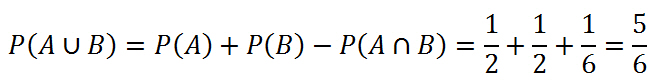Операции над событиями. Теория вероятностей
Пересечение событий
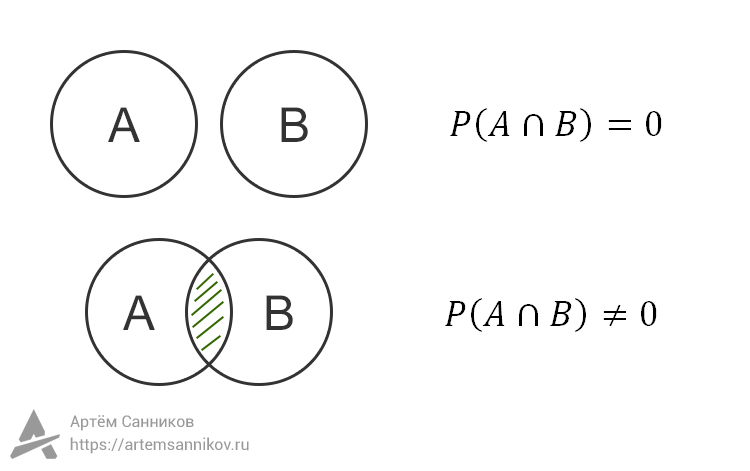
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.
События не пересекаются
Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.
События пересекаются
Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.
Объединение событий
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.
События не пересекаются
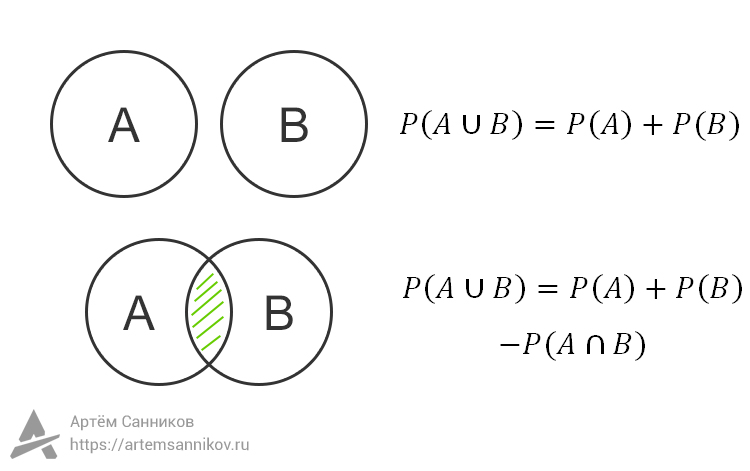
Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).
События пересекаются
Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)
Независимые события
События A и B независимы, если наступление одного события не влияет на другое событие.
Практический пример
Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:
- 1 очко = ω1;
- 2 очка = ω2;
- 3 очка = ω3;
- 4 очка = ω4;
- 5 очков = ω5;
- 6 очков = ω6.
Событие A: выпало > 3 очков
Событие B: выпало нечетное число очков
Чтобы приступить к решению задачи выполняем анализ событий.
Анализ события A: этому событию соответствует три элементарных исхода { ω4, ω5, ω6}
Анализ события B: этому событию соответствует три элементарных исхода{ ω1, ω3, ω5}
После анализа событий приступаем к пошаговому решению.
Рассмотрим теперь пересечение события A и B, то есть у нас должно выпасть > 3 очков и при этом число должно быть нечётное. В этом случае у нас есть один элементарный исход: { ω5}.
Отсюда мы можем посчитать вероятность этого события:
- n – элементарный исход, который удовлетворяет нашим условиям;
- N – общее количество исходов.
Далее рассмотрим объединение событий A и B. В данном случае у нас будет следующий набор элементарных условий { ω1, ω3, ω4, ω5, ω6}
Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:
По факту мы решили задачу, но мы можем её решить намного быстрее, если воспользуемся формулой, которую изучили ранее:
- Вероятность P(A) – выпало > 3 очков
- Вероятность P(B) – выпало нечётное число
- Вероятность P(A ∩ B) – пересечение событий A и B
Метки: Математика, Теория вероятностей.
Анализ данных • 14 декабря 2022 • 5 мин чтения
Совместные и несовместные события в анализе данных
Аналитики применяют теорию вероятностей, чтобы предсказать развитие бизнеса. Результат расчётов зависит от того, как взаимодействуют события между собой. Расскажем, какие виды событий есть и как посчитать их вероятность.
- Термины, которые используются в статье
- Противоположные события
- Несовместные события
- Совместные события
- Алгебра событий
- Как использовать совместные и несовместные события в анализе данных
- Совет эксперта
Термины, которые используются в статье
Пространство исходов — это множество всех исходов. Оно описывает все возможные варианты того, что может случиться в результате эксперимента. Обозначается буквой омега Ω.
Событие — это подмножество Ω, удовлетворяющее определённым условиям.
Например, «число очков на кубике чётное» — это событие.
Вероятность произвольного случайного события всегда принимает значения от 0 до 1, где 0 — событие невозможно, а 1 — событие точно произойдёт.
Анализ больших данных: зачем он нужен и кто им занимается
Противоположные события
Событие A̅ противоположно событию A, если состоит из тех исходов Ω, которых нет в A.
Из определения противоположных событий следуют два свойства:
● события А и A̅ и образуют всё пространство исходов,
● события А и A̅ не могут произойти одновременно.
Из двух событий А и A̅ наступить может только одно. При этом исходов в каждом событии может быть несколько.
Примеры:
● А = «на кубике выпало кратное 3 число» = {3, 6} и противоположное A̅ = «на кубике выпало не кратное 3 число» = {1, 2, 4, 5}
● A = «в задании с 5 попытками игрок сделал меньше 3 попыток» = {0, 1, 2, 3} и противоположное «в задании с 5 попытками игрок сделал больше 3 попыток = {4, 5}.
Противоположные события — частный случай несовместных событий.
Несовместные события
Несовместные события похожи на противоположные — они тоже не могут произойти одновременно. Появление одного события исключает появление всех остальных, несовместных с ним. Но есть и важное отличие: несовместных событий может быть сколько угодно, не только два.
Пример. Оплатить покупку в онлайн-магазине можно несколькими способами: картой на сайте, наличными при получении, в рассрочку от магазина или в кредит от банка. Все способы доступны, но пользователь должен выбрать только один из них.
Для набора событий А1, А2, … Аn это условие записывают так:
Аi ∩ Аj = Ø для всех
Пример. В некотором ресторане есть только четыре блюда дня: овощная грилата, суп из шампиньонов, салат по-мексикански и сэндвич с тунцом. И каждый день можно выбрать лишь одно из них. Исследователь, который постоянно заказывает еду из этого ресторана, хочет предсказать блюдо дня на завтра. На основе исторических данных он выяснил, что частота появления грилаты составляет ≈ 34%, супа ≈ 12%, салата ≈ 7%, а сэндвича ≈ 47%
На языке теории вероятностей это выглядит так:
● пространство исходов Ω = {грилата, суп, салат, сэндвич} ;
● P(грилата) = 0.34, Р(суп) = 0.12, Р(салат) = 0.07, Р(сэндвич) = 0.47.
В этом примере события образуют полную группу — набор несовместных событий, которые в объединении дают всё пространство исходов Ω.
Совместные события
События А и B называют совместными, если A ∩ B ≠ Ø .
Пример. Производитель корма провёл онлайн-опрос, чтобы узнать, какие питомцы живут у покупателей. Варианты ответа: собака, кошка, хомяк. У 65% есть собаки, 81% с кошками и 15% c хомячками. При этом у 52% респондентов есть и кошка, и собака, а у 9% — хомяк с собакой.
Совместные события, как и несовместные, необязательно дают в объединении всё пространство исходов Ω. В наборе из нескольких событий часть могут быть совместными друг другу, часть — несовместными.
Разные типы событий на диаграммах Эйлера.
Алгебра событий
Правило суммы для противоположных событий: вероятность объединения противоположных событий равна сумме их вероятностей, которая, в свою очередь, равна 1.
P(A) = 1 — P(A̅).
Правило суммы для несовместных событий: вероятность объединения несовместных событий равна сумме вероятностей каждого события.
P(A ∪ B) = P(A) + P(B)
Правило суммы для совместных событий: чтобы найти вероятность объединения двух совместных событий, нужно из суммы их вероятностей вычесть вероятность их пересечения.
P(A ∪ B) = P(A) + P(B) — P(A ∩ B)
Формула включений-исключений для трёх событий:
P(A ∪ B ∪ C ) = P(A) + P(B) +P(C) — P(A ∩ B) — P(A ∩ C) — P(B ∩ C) + P(A ∩ B ∩ С)
Как использовать совместные и несовместные события в анализе данных
Пример. Поисковый сервис с равной вероятностью размещает рекламный баннер клиента слева от поисковой выдачи, справа или внутри неё. Нужно изучить, как работают алгоритмы. Чему равна вероятность, что из пяти поисковых запросов хотя бы в одном аналитик увидит рекламу слева от поисковой выдачи?
Решение. «Хотя бы один» — маркер того, что проще искать вероятность через обратное событие. Посчитаем вероятность противоположного события:
Тогда вероятность искомого события находится по формуле для противоположных событий:
Пример. Компания предлагает пользователям индивидуальную и семейную подписку на кино и музыку. Известно, что какая-либо подписка есть у клиентов. Сколько клиентов компании не имеют никакой подписки?
Решение. Всех клиентов компании можно поделить на три группы:
● A — есть индивидуальная подписка;
● B — есть семейная подписка;
● C — нет подписки.
В совокупности они образуют полную группу событий. Тогда P(A) + P(B) + P(C) = 1.
Известно, что клиентов с подпиской 60%, то есть P(A ∪ B) = 0.6 = P(A) + P(B).
Подставляя в формулу выше, получаем P(C) = 0.4 = 40% клиентов без подписки.
Пример. Аналитик изучает источники трафика. В таблице данные по новым пользователям.
Источник трафика для каждой записи только один. context означает, что пользователь пришёл из контекстной рекламы; email — из рассылки на почту; источники None, other и undef не дают подробностей.
На основе этой таблицы аналитик прогнозирует вероятность источника, из которого придёт новый пользователь. Например, доля источника context равна
Это значение и принимают за вероятность. Какая вероятность того, что новый пользователь придёт из источников без подробностей (None, other и undef)?
Решение. Источник трафика может быть только один, поэтому события «пользователь пришёл из данного источника» несовместны. Вероятности можно сложить:
Эти задачи — примеры того, как аналитики применяют теорию вероятностей в своей работе.
В математике главное — практика. Поэтому знание правил лучше закреплять решением задач. Сделать это можно в бесплатном тренажёре «Основы математики для цифровых профессий». В нём более 1000 задач с автоматической проверкой и подробными решениями.
Повторите математику, чтобы решать рабочие задачи
Вспомните проценты, алгебру и другие темы посложнее в бесплатном тренажёре «Основы математики для цифровых профессий».
Совет эксперта
Евгений Григоренко
Учёные придумали рассматривать события, чтобы связать реальность с математикой и строго описать понятие вероятности. На самом деле событие — это математическое обозначение любого возможного явления, для которого интересно оценивать шансы. А/B-тесты не будут преградой, если тренироваться на простых задачах.
Автор курса по математике
Как пересечение и объединение множеств используются в анализе данных
Чем занимается аналитик данных, почему он всем так нужен и как освоить эту профессию
Итак, сегодня у нас из теории вероятностей, задачи об объединении несовместных событий. Мы уже рассмотрели задачи на подбрасывание монеты и кубика, а также задачи средней трудности из ЕГЭ о пересечении независимых событий.
Объединение несовместных событий
Задача 4.1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Ромб», равна 0,1. Вероятность того, что это вопрос на тему «Описанная окружность», равна 0,15. Вопросов, относящихся одновременно к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Пусть событие А означает, что школьнику достался вопрос по теме «Ромб», событие В — вопрос по теме «Описанная окружность». По условию Р(А)= 0,1, Р(В) = 0,15. По условию события А и В несовместны. Искомая вероятность равна = Р(А) + Р(В) = 0,1+ 0,15 = 0,25.
Ответ: 0,25.
Задача 4.2. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Решение.
1-й способ.
Обозначим через А событие «кофемолка прослужит больше года, но меньше двух лет», через В событие «кофемолка прослужит больше двух лет». События А и В несовместны (кофемолка не может прослужить меньше двух лет и одновременно больше двух лет). Объединением событий А и В является событие А и В «кофемолка прослужит больше года». По условию = 0,93, Р(В) = 0,81. Так как А и В несовместны, то
= Р(А) + Р(В), откуда Р(А) =
— Р(В) = 0,93 — 0,81 = 0,12.
2-й способ.
Будем рассуждать о том, когда может сломаться кофемолка. Она может сломаться уже на первом году работы, может сломаться на втором году работы, а может проработать более двух лет и сломаться потом. Будем заполнять следующую таблицу:
| Событие | сломалась на первом году | сломалась на втором году | сломалась после двух лет работы |
| Вероятность |
Так как вероятность события «кофемолка прослужит больше года» равна 0,93, то вероятность противоположного события «кофемолка сломалась на первом году» равна 1 — 0,93 = 0,07. Вероятность события «кофемолка сломалась после первых двух лет работы» по условию равна 0,81. Вносим найденные значения в таблицу.
| Событие | сломалась на первом году | сломалась на втором году | сломалась после двух лет работы |
| Вероятность | 0,07 | 0,81 |
В таблице перечислены три несовместных события, одно из которых обязательно произойдёт. Поэтому сумма вероятностей в таблице должна быть равна 1. Следовательно, незаполненное искомое значение можно вычислить как 1 — 0,07 — 0,81=0,12.
Ответ: 0,12.
Задача 4.3. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 25 пассажиров, равна 0,91. Вероятность того, что окажется меньше 18 пассажиров, равна 0,39. Найдите вероятность того, что число пассажиров будет от 18 до 24.
Решение.
Обозначим через А событие «в автобусе менее 18 пассажиров», через В событие «в автобусе от 18 до 24» пассажиров. Тогда А U В это событие «в автобусе менее 25 пассажиров». По условию Р (А U В) = 0,91, Р(А) = 0,39. Так как события А и В несовместны, то = Р(А) + Р(В), откуда 0,91 = 0,39 + Р(В), Р(В) = 0,52. Ответ: 0,52.
Задачи об объединении пересечений событий
Задача 4.4. Ковбой Билл попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,25. На столе лежит 5 револьверов, из них только 2 пристрелянные. Ковбой Билл видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Билл попадёт в муху.
Решение.
Так как из 5 револьверов 2 пристреляны, то вероятность схватить пристрелянный револьвер равна . Вероятность схватить один из трёх непристрелянных револьверов равна
.
Обозначим через А событие «Билл схватит пристрелянный револьвер и попадёт из него в муху». Так как события «Билл схватит пристрелянный револьвер» и «Билл попадёт из пристрелянного револьвера в муху» независимы, то Р(А) = .
Аналогично вероятность события В «Билл схватит непристрелянный револьвер и попадёт из него в муху» равна Р(В) = . События А и В несовместны (Билл не может одновременно стрелять как из пристрелянного, так и из непристрелянного револьвера). Искомая вероятность равна
= Р(А)+Р(В) = 0,32+0,15=0,47
Ответ: 0,47.
Задача 4.5. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,98. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,08. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Решение.
Для отбраковки неисправной батарейки должны произойти два независимых события: «линия произвела неисправную батарейку» и «неисправная батарейка забракована». Вероятность события А «произведена и забракована неисправная батарейка» равна Р(А) = 0,05 • 0,98 = 0,049.
Исправную батарейку линия производит с вероятностью 1- 0,05 = 0,95. Для отбраковки исправной батарейки должны произойти два независимых события: «линия произвела исправную батарейку» и «исправная батарейка забракована». Вероятность события В «произведена и забракована исправная батарейка» равна Р(В) = 0,95 • 0,08 = 0,076.
События А и В несовместны. Искомая вероятность равна = Р(А) + Р(В) = 0,049 + 0,076 = 0,125.
Ответ: 0,125.
Задача 4.6. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение.
1-й способ.
Так как вероятности выигрыша и проигрыша равны 0,3, то вероятность ничьей равна 1-0,3-0,3 = 0,4. Команда выходит в следующий круг либо после двух выигрышей, либо после выигрыша и ничьей.
1)Вероятность события А «команда выиграла оба матча» по формуле пересечения независимых событий находим как Р(А) = .
2)Вероятность события В «команда выиграла первый матч, закончила вничью второй матч» равна Р(В) =
З. Вероятность события С «команда закончила вничью первый матч, выиграла второй матч» равна Р(В) =
События А, В, С попарно несовместны, вероятность их объединения равна = Р(А)+Р(В)+Р(С) = 0,09 + 0,12 + 0,12 = 0,33.
2-й способ.
Составим таблицу возможных результатов матчей и вероятностей этих результатов.
|
Второй матч |
||||
| победа
Р=0,3 |
ничья
Р=0,4 |
поражение Р=0,3 |
||
| Первый матч | победа Р = 0,3 | 0,09 | 0,12 | 0,09 |
| ничья Р = 0,4 | 0,12 | 0,16 | 0,12 | |
| поражение Р = 0,3 | 0,09 | 0,12 | 0,09 |
Числа в ячейках получаются по принципу таблицы умножения (умножение вероятностей соответствующих результатов первого и второго матчей), так как вероятности результатов первого и второго матча не зависят друг от друга. Жирным шрифтом в таблице выделены вероятности тех результатов, при которых команда выходит в следующий круг. Искомая вероятность равна 0,09 + 0,12 + 0,12 = 0,33.
Ответ: 0,33.
Задача 4.7. Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 60% этих стёкол, вторая-40%. Первая фабрика выпускает 4% бракованных стёкол, а вторая — 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение.
Вероятность купить стекло первой фабрики равна 0,6. Вероятность брака в стекле первой фабрики равна 0,04. Вероятность события А «куплено бракованное стекло первой фабрики» находим по формуле для пересечения независимых событий: Р (А) = 0,6 • 0,04 = 0,024.
Вероятность купить стекло второй фабрики равна 0,4. Вероятность брака в стекле второй фабрики равна 0,03. Вероятность события В «куплено бракованное стекло второй фабрики» равна Р(В) = 0,4 • 0,03 = 0,012.
Искомая вероятность равна вероятности объединения несовместных событий А и В.
= Р(А) + Р(В) = 0,024 + 0,012 = 0,036.
Ответ: 0,036.
Задачи о частоте
Задача 4.8. Вероятность того, что новый DVD — проигрыватель в течение года поступит в гарантийный ремонт, равна 0,05. В некотором городе из 2000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступили 130 штук. Насколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение.
Частота события «гарантийный ремонт» равна . От вероятности она отличается на 0,065 — 0,05 = 0,015.
Ответ: 0,015.
Подведем итог
После изучения материала по решению простых задач по теории вероятностей рекомендую выполнить задачи для самостоятельного решения, которые мы публикуем на нашем канале Telegram.
Также рекомендую изучить простые задачи по теории вероятностей, «Центральные и вписанные углы. Задание № 3 ЕГЭ» и другие уроки по решению заданий ЕГЭ по математике, которые представлены на нашем канале Youtube.
Спасибо, что поделились статьей в социальных сетях
Источник «Подготовка к ЕГЭ. Математика.Теория вероятностей». Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
Операции над событиями. Диаграммы Эйлера – Венна
Содержание
В теории вероятностей случайными событиями являются подмножества множества элементарных исходов Ω .
Над событиями, как и над любыми множествами, можно совершать следующие операции.
Произведение (пересечение) двух событий
Операцию произведения (пересечения) двух событий A и B обозначают
, или AB, или
.
ОПРЕДЕЛЕНИЕ 1. Произведением (пересечением) двух событий A и B называют такое событие, которое состоит из всех элементов, входящих как в событие A , так и в событие B (рис. 1).
Рис.1
Сумма (объединение) двух событий
Операцию суммы (объединения) двух событий A и B обозначают
A + B или
ОПРЕДЕЛЕНИЕ 2. Суммой (объединением) двух событий A и B называют такое событие, которое состоит из элементов события A и элементов события B (рис. 2).
Рис.2
Разность двух событий
Операцию разности двух событий A и B обозначают
A B
ОПРЕДЕЛЕНИЕ 3. Разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B (рис. 3).
Рис.3
ЗАМЕЧАНИЕ 1. Разностью событий B и A является событие B A , изображенное на рисунке 4.
Рис.4
Симметрическая разность двух событий
Операцию симметрической разности двух событий A и B обозначают
ОПРЕДЕЛЕНИЕ 4 . Симметрической разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B , а также из тех элементов события B , которые не входят в событие A (рис. 5).
Рис.5
Переход к противоположному событию
Событие, противоположное к событию A , обозначают
или AC
ОПРЕДЕЛЕНИЕ 5. Противоположным событием к событию A называют событие, состоящее из тех элементов всего множества элементарных событий Ω , которые не входят в событие A (рис. 6).
Рис.6
ЗАМЕЧАНИЕ 2. Справедлива формула
ОПРЕДЕЛЕНИЕ 6. Событие Ω называют достоверным событием, пустое множество называют невозможным событием.
ЗАМЕЧАНИЕ 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .
Объединение несовместных событий.
Объединение несовместных событий.
Два события A и B называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событий A и B:
P(A U B) =P(A) + P(B)
Пример: На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0, 1. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0, 27. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение. Пусть событие А заключается в нахождении вопроса по теме «Вписанная окружность», тогда событие В заключается в нахождении вопроса на тему «Параллелограмм». События А и В являются несовместными так как данные события не могут произойти одновременно, иначе говоря если произойдет одно событие, другое произойти уже не может, следовательно для решения данной задачи нам необходимо найти объединение событий для этого мы находим их сумму.
0. 27+0. 1=0. 37
Ответ: вероятность того, что на экзамене школьнику достанется вопрос по одной из двух тем равна 0. 37
Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или не появления другого события.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей событий A и B: