Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу: 
Ответ: 424.
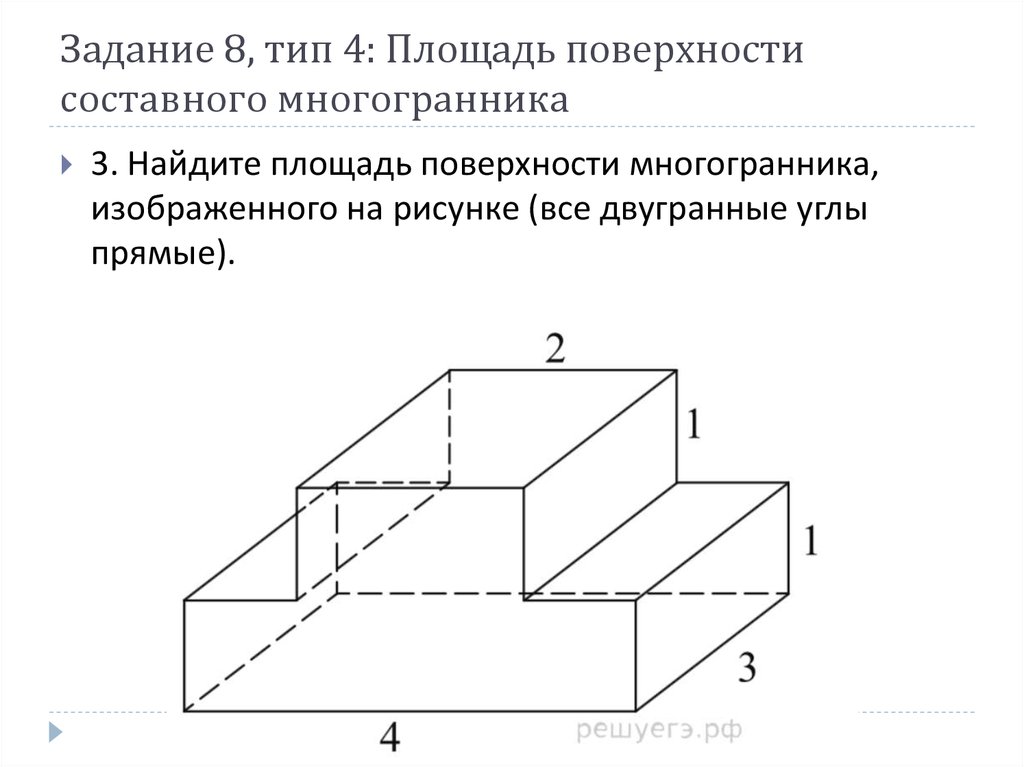
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
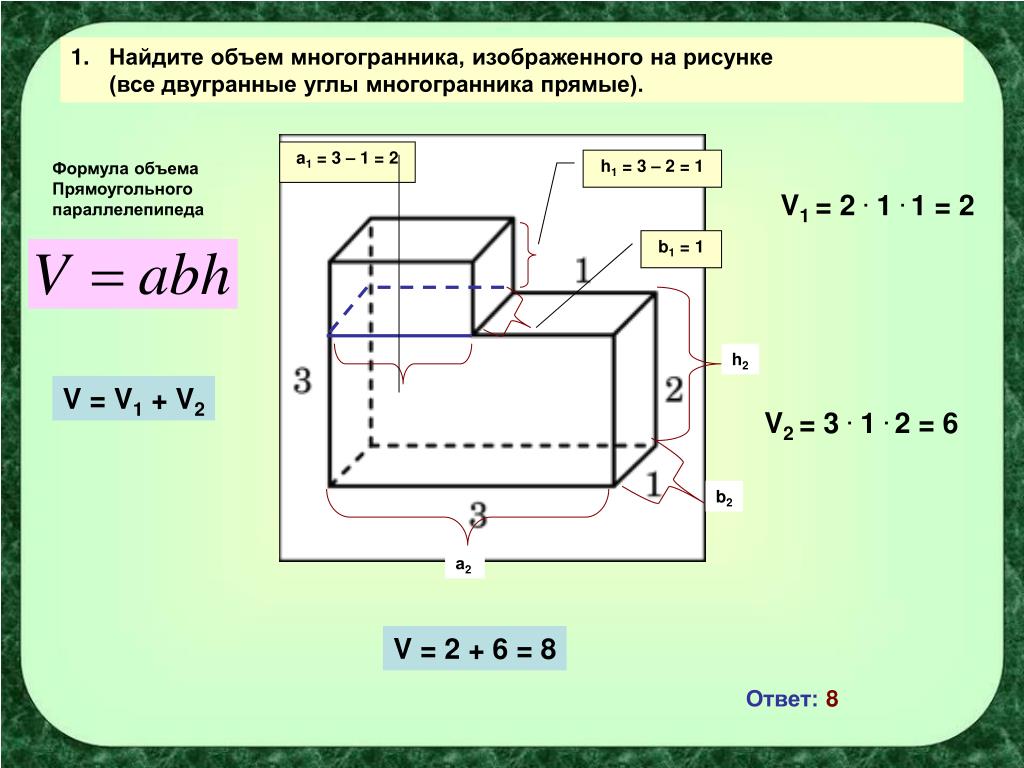
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту
Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, 
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Содержание:
Объёмы поверхностей геометрических тел:
То, чем в предыдущие эпохи занимались только зрелые умы ученых мужей, в более позднее время стало доступным для понимания юношей.
С древних времен люди применяли геометрию для решения конкретных житейских проблем — нахождения объемов сосудов, строений и кораблей, количества краски, необходимой для ремонта помещения. На основании практического опыта были разработаны методы вычисления объемов тел и площадей поверхностей. Но нахождение соответствующих формул, а тем более их доказательств заняло немало страниц в истории геометрической науки. Многие выдающиеся ученые внесли свой вклад в развитие теории объемов, а популяризаторы математики — в упрощение и доступное изложение этой теории.
Основной целью данной главы является формирование представлений об объемах и площадях поверхностей, обоснование соответствующих формул для основных пространственных фигур. Вы. научитесь использовать различные методы нахождения объемов, как строго геометрические, так и те, которые объединяют в себе геометрию и начала анализа. При изучений объемов тел полезно будет вспомнить и систематизировать материал о площадях фигур на плоскости. Подходы, которые применялись для получения основных формул площадей, будут надежным фундаментом для построения теории объемов.
В данной главе речь пойдет о всех основных фигурах, которые вы изучали в течение года, в частности о тесной связи многогранников и тел вращения. Это даст вам возможность, с одной стороны, вспомнить основные факты из курса геометрии, а с другой — на основании формул для площадей поверхностей многогранников получить соответствующие результаты для тел вращения.
Задачи данной главы содержат много геометрических конфигураций, что позволит вам переосмыслить весь курс стереометрии с точки зрения применения своих знаний на практике, в частности для нахождения, пожалуй, самых распространенных в жизни геометрических величин — объемов и площадей поверхностей. Ради этого бесценного опыта вы и изучали, в конце концов, геометрию в пространстве.
Объемы
Понятие объема хорошо известно на уровне повседневного опыта: мы покупаем пакет сока определенного объема, рассчитываем, какой объем займет в квартире новая мебель, берем для приготовления блюда кастрюлю соответствующего объема. Придадим этим наглядным представлениям об объеме тела определенную математическую строгость.
Понятие объема многогранников
Для дальнейших рассуждений полезно объединить практический опыт и известную уже теорию площадей многоугольников. По аналогии с ней мы и будем строить теорию объемов пространственных тел, в первую очередь многогранников.
Объем характеризует величину части пространства, которую занимает геометрическое тело, и измеряется, как и площадь, в определенных единицах. Единицей измерения площадей является площадь единичного квадрата, а за единицу измерения объема принимается объем единичного куба, то есть куба, ребро которого равно единице длины. Например, если за единицу измерения длины принимается 1 мм, 1 см, 1 дм или 1 м, то за единицу измерения объема принимается объем куба с ребром 1 мм, 1 см, 1 дм или 1 м. Соответствующая единица объема называется кубическим миллиметром (1 мм3), кубическим сантиметром (1 см3), кубическим дециметром или литром (1 дм3 или 1 л), кубическим метром (1 м3). Таким образом, вычисление объемов тел разной формы основано на сравнении с объемом единичного куба.
Измерить объем тела на практике можно, например, погрузив его в воду и подсчитав количество вытесненной телом воды. Но во многих случаях это не целесообразно, поэтому очень полезно вывести и научиться применять формулы для вычисления объемов. Соответствующая теория основана на аксиомах объема многогранников.
- Равные многогранники имеют равные объемы.
- Бели многогранник составлен из нескольких многогранников, то его объем равен сумме объемов этих многогранников.
- Объем куба с ребром, равным единице длины, равен единице объема.
Итак, объем многогранника — это положительная величина, Числовое значение которой удовлетворяет аксиомам объема. : — Как правило, объем обозначают буквой V.
Приведенные аксиомы имеют и практическую основу. Действительно, все пакеты, имеющие форму прямоугольного параллелепипеда и одинаковые размеры, содержат одинаковое количество сока.
Тела, имеющие равные объемы, называются равновеликими.
Если же каждый из двух пакетов можно разлить в одинаковое количество маленьких пакетиков, то сумма объемов этих пакетиков будет равна объему каждого из них, то есть данные пакеты имеют одинаковый объем.
Тела, составленные из одних и тех же многогранников, называются равносоставленными. Например, равносоставленными будут тела, изображенные на рисунке 190, а, б: прямая треугольная призма и прямой параллелепипед. Действительно, каждая из этих фигур составлена из двух одинаковых прямых призм, таких как на рисунке 190, в.
Очевидно, что объемы равносоставленных многогранников равны по второй аксиоме. Интересно, что обратное утверждение неверно (в отличие от аналогичной теоремы для площадей). Так, многогранники равного объема не всегда можно разбить на конечное число равных многогранников. В частности, куб и правильный тетраэдр равных объемов (рис. 190) не являются равносоставленными.
Объем параллелепипеда
Простейшей фигурой с точки зрения вычисления объема является прямоугольный параллелепипед.
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 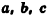
Приведем рассуждения, на которых основано доказательство данной теоремы.
Сначала рассмотрим прямоугольный параллелепипед с измерениями а, 1, 1. Так как в отрезке а единица измерения длины помещается а раз, то единичный куб помещается в параллелепипед также а раз. Значит, объем прямоугольного параллелепипеда равен а (рис. 191, а).
Аналогично объем прямоугольного параллелепипеда с измерениями 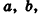
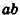
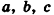
Полное доказательство данной теоремы приведено в Приложении 2.
Следствие (формула объема куба)
Объем куба равен кубу его ребра:
где а — ребро куба.
Нам известно, что площадь прямоугольника равна произведению двух его измерений, а параллелограмма — произведению его стороны на проведенную к ней высоту. По аналогии нетрудно предположить, что объем произвольного параллелепипеда также можно найти через площадь основания и соответствующую высоту.
Теорема (формула объема параллелепипеда)
Объем параллелепипеда равен произведению площади его основания на высоту:
где 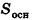
Доказательство:
Очевидно, что для прямоугольного параллелепипеда данная формула верна. Докажем ее для наклонного параллелепипеда 
При описанном преобразовании параллелепипеда площадь его основания и высота сохраняются, а две боковые грани становятся перпендикулярными плоскости основания ABC. Если выполнить аналогичное преобразование с помощью плоскостей, проходящих через АВ и DC перпендикулярно основанию ABCD, получим прямой параллелепипед с основанием ABCD, равновеликий исходному. При этом высоты параллелепипедов также сохраняются.
Теперь проведем через точки А я В плоскости, перпендикулярные АВ (рис. 193). Дополняя прямой параллелепипед одной треугольной призмой (I) и отсекая равную ей другую призму (2), получим прямоугольный параллелепипед, равновеликий предыдущему.
Объем полученного прямоугольного параллелепипеда равен 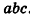
основания и высота сохраняются, то и объем исходного параллелепипеда можно вычислить с помощью полученной формулы. Итак, объем наклонного параллелепипеда
Таким образом, объем произвольного параллелепипеда вычисляется по формуле
Теорема доказана.
Пример №1
В основании наклонного параллелепипеда лежит прямоугольник со сторонами 3 см и 4 см. Боковое ребро параллелепипеда равно 6 см. Найдите объем данного параллелепипеда, если две его боковые грани перпендикулярны плоскости основания, а две другие наклонены к ней под углом 30°.
Решение:
Пусть дан параллелепипед 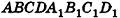
Пусть грани 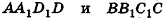
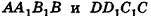
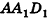
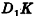
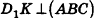
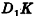
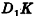
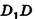
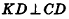
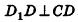
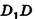
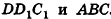
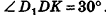
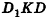
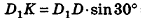
Таким образом,
Ответ: 36 см3.
Объем призмы
На плоскости для получения формулы площади треугольника было удобно дополнить треугольник до параллелограмма. Далее, для получения формулы площадей других многоугольников, целесообразно было разбить их на треугольники. Применим аналогичные приемы для вывода формулы объема призмы.
Теорема (формула объема призмы)
Объем призмы равен произведению площади ее основания на высоту:
где 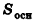
Доказательство:
Пусть дана треугольная призма 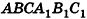
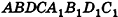
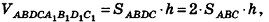
Применим только что выведенную формулу объема треугольной призмы к рассмотрению произвольной призмы.
Разобьем основание призмы на треугольники, а призму — на соответствующие треугольные призмы с высотой h (рис. 196).
По аксиоме, объем данной призмы равен сумме объемов составляющих ее треугольных призм:
где 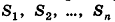
Теорема доказана.
Пример №2
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения: 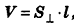
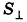
Решение:
Рассмотрим наклонную призму F1 с ребром АА1 = I (рис. 197). Проведем два ее перпендикулярных сечения, расстояние между плоскостями которых I и которые не имеют с данной призмой общих точек. При этом получим прямую призму F2 и многогранник F3 (рис. 197). Многогранник, гранник, как совмещаются параллельным переносом на вектор 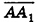
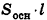
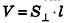
Объем цилиндра
При обосновании формулы площади круга в планиметрии мы использовали вписанные в окружности и описанные около них многоугольники. Применим аналогичные рассуждения и в пространстве, заменив круг на цилиндр, а многоугольники — на призмы. Дадим соответствующие определения.
Определение:
Прямая призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра.
При этом цилиндр называется описанным около призмы. Очевидно, что боковые ребра призмы — образующие цилиндра, а высоты прямой призмы и описанного около нее цилиндра равны (рис. 198).
Определение:
Прямая призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра.
При этом цилиндр называется вписанным в призму (рис. 199). Очевидно, что высоты прямой призмы и вписанного в нее цилиндра равны.
Теорема (формула объема цилиндра)
Объем цилиндра равен произведению площади его основания на высоту:
где 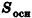
Доказательство:
Впишем в данный цилиндр радиуса R и высоты h правильную п-угольную призму с площадью основания S’n и опишем около него правильную n-угольную призму с площадью основания 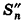
Отсюда следует, что при неограниченном возрастании п объемы вписанных призм 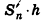
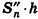
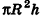
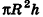
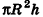
Теорема доказана.
Пример №3
Основание прямой призмы — треугольник со стороной с-и прилежащими к ней углами 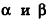
Решение:
Пусть дана прямая треугольная призма 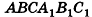
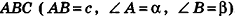
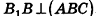
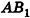
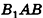
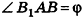
Рассмотрим цилиндр, описанный около данной призмы. Его основания описаны около оснований призмы, высота равна высоте призмы.
По теореме синусов для треугольника ABC имеем:
Из прямоугольного треугольника
Следовательно, объем цилиндра равен:
Ответ:
Объемы пирамиды, конуса и шара
Рассмотрим способ вычисления объемов тел, в основе которого лежит понятие интеграла, известное из курса алгебры и начал анализа.
Общая формула объема
Пусть тело Т, объем которого требуется вычислить, расположено между двумя параллельными плоскостями 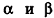
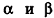
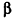
Будем рассматривать случай, когда любое сечение тела Ф(х) плоскостью, перпендикулярной-оси Ох и пересекающей эту ось в точке (х;0;0), является кругом или многоугольником (такой случай возможен, если Ф(х) — точка).
Обозначим площадь фигуры Ф(х) через S(x). Допустим, что S(x) — непрерывная функция при 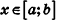
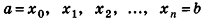
Эти плоскости разобьют тело Т на n тел: 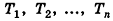
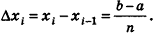
Учитывая, что объем цилиндра и призмы равен произведению площади основания на высоту, то есть 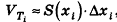
При неограниченном возрастании n правая часть данной формулы приближается сколь угодно близко к объему тела Т. С другой стороны, так как S(x) непрерывна на 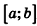
Таким образом, мы получили формулу для вычисления объема тела с помощью интеграла. Будем называть ее интегральной формулой объема.
Из этой формулы вытекает интересное и удобное в применении следствие, формулировка которого принадлежит итальянскому математику Бонавентуре Кавальери.
Принцип Кавальери
Если при пересечении двух тел F1 и F2 плоскостями, параллельными одной и той же плоскости а, в сечениях получаются фигуры с равными площадями, то объемы данных тел равны.
Это утверждение легко вывести из интегральной формулы объема, если расположить систему координат так, чтобы ось Ох была перпендикулярна плоскости а (рис. 204). Применение интеграла и принципа Кавальери позволяет значительно упростить нахождение формул, выражающих объемы многих важных тел.
Объем пирамиды и конуса
В пунктах 15.3 и 15.4 мы установили, что объемы призмы и цилиндра определяются одной и той же формулой:
Поэтому вполне естественно предположить, что будут совпадать формулы для объемов пирамиды и конуса.
Теорема (формула объема пирамиды)
Объем пирамиды равен трети произведения площади основания на высоту:
где 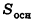
Доказательство:
Разместим пирамиду в системе координат так, чтобы ось Ох была направлена вдоль высоты, а основание’ принадлежало бы плоскости 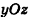
Отсюда
Применяя теперь для пирамиды интегральную формулу объема, получим:
Теорема доказана.
Следствие (формула объема усеченной пирамиды)
Объем усеченной пирамиды вычисляется по формуле:
где h — высота усеченной пирамиды, 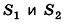
Доказательство:
Дополним данную усеченную пирамиду до полной с высотой Н (рис. 206). Тогда высота дополняющей пирамиды будет равна H-h. Из подобия полной и дополняющей пирамид, площади оснований которых равны 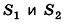
По аксиомам объема, объем усеченной пирамиды равен разности объемов полной и дополняющей пирамид. Следовательно,
Формула доказана.
Заметим, что при доказательстве теоремы об объеме пирамиды и ее следствия, кроме интегральной формулы объема, мы применили только тот факт, что плоскость, параллельная основанию, отсекает пирамиду, для площади основания S(x) и высоты h-x которой верна формула
Но эта формула, по доказанному в п. 13.2, также верна и для конуса (рис. 207). Поэтому аналогичными формулам объема и их доказательствам для пирамиды и усеченной пирамиды будут формулы объема и их доказательства для конуса и усеченного конуса.
Теорема (формула объема конуса)
Объем конуса равен трети произведения площади основания на высоту:
где 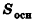
Следствие (формула объема усеченного конуса)
Объем усеченного конуса вычисляется по формуле
где h — высота усеченного конуса, 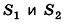
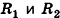
С помощью вписанных и описанных призм мы вывели формулу для объема цилиндра. Подобную связь можно установить также для конусов и пирамид.
Определение:
Пирамида называется вписанной в конус, если их вершины совпадают, а основание пирамиды вписано в основание конуса.
При этом конус называется описанным около пирамиды.
Очевидно, что высоты пирамиды и описанного конуса равны, а боковые ребра пирамиды являются образующими конуса (рис. 208).
Определение:
Пирамида называется описанной около конуса, если их вершины совпадают, а основание пирамиды описано около основания конуса.
При этом конус называется вписанным в пирамиду.
Очевидно, что высоты пирамиды и вписанного конуса равны, а высоты боковых граней пирамиды являются образующими конуса (рис. 209).
Рассмотрим правильные л-угольные пирамиды, вписанные в данный конус, и правильные л-угольные пирамиды, описанные около него (рис. 210).
Если число n сторон оснований этих пирамид неограниченно возрастает, то площади их оснований стремятся к площади круга, лежащего в основании конуса. Следовательно, их объемы стремятся 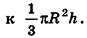
Из этих рассуждений становится понятным другое обоснование формулы объема конуса
Объем шара и его частей
Непосредственно получить только из геометрических рассуждений формулу для объема шара очень сложно. Но с помощью интегральной формулы объема и принципа Кавальери доказательство соответствующих результатов является простым и наглядным.
Теорема (формула объема шара)
Объем шара радиуса R вычисляется по формуле
Доказательство:
Найдем сначала объем полушара, применив принцип Кавальери.
Пусть дан полушар Fl радиуса R. На плоскость а, содержащую основание полушара, поставим цилиндр, радиус и высота которого также равны R. В цилиндр впишем конус, вершина которого совпадает с центром основания цилиндра в плоскости а, а основание — с другим основанием цилиндра (рис. 211).
Сравним объем V1 полушара с объемом V2 тела F2, ограниченного нижним основанием цилиндра и боковыми поверхностями цилиндра и конуса.
Проведем плоскость 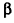
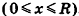
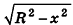
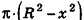
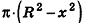
Объем шара вдвое больше объема полушара, следовательно, вычисляется по формуле 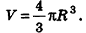
Пример №4
Сечение шара, удаленное от его центра на 1 см, имеет площадь 8л см2. Найдите объем шара.
Решение:
Пусть дан шар с центром О. Сечение шара некоторой плоскостью а является кругом с центром 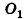
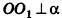
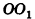
Пусть точка К сферы, ограничивающей шар, принадлежит данному сечению (рис. 212). Тогда площадь сечения равна 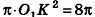
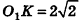
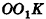
По формуле объема шара
Ответ:
Найдем теперь объемы частей шара.
Определение:
Шаровым сегментом называется часть шара, отсекаемая от него некоторой плоскостью.
На рисунке 213 плоскость сечения, проходящая через точку В, разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется основанием этих сегментов, а длины отрезков диаметра, перпендикулярного плоскости сечения,— высотами сегментов. Так, на рисунке 213 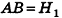
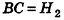
Теорема (формула объема шарового сегмента)
Объем шарового сегмента вычисляется по формуле
где R — радиус шара, Н — высота сегмента.
Доказательство:
Применим для шарового сегмента интегральную формулу объема.
Введем декартову систему координат так, чтобы ее начало совпадало с центром шара.
Тогда часть шара, ограниченная плоскостями 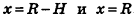
Радиус сечения шарового сегмента плоскостью, пересекающей ось Ох в точке (х;0;0), равен 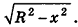
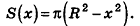
Теорема доказана.
Заметим, что при Н -2R из только что доказанной формулы следует еще один способ нахождения формулы объема шара:
Определение:
Шаровым сектором называется тело, ограниченное сферической поверхностью шарового сегмента и боковой поверхностью конуса, основанием которого является основание сегмента, а вершиной — центр шара.
Очевидно, что если шаровой сегмент меньше полушара, его дополняют конусом для получения шарового сектора; если же шаровой сегмент больше полушара, то для получения шарового сектора конус из него удаляют (рис. 215).
Теорема (формула объема шарового сектора)
Объем шарового сектора вычисляется по формуле
где R — радиус шара, Я — высота соответствующего шарового сегмента.
Доказательство:
Рассмотрим случай шарового сектора, высота Я соответствующего шарового сегмента для которого меньше R (рис. 216).
Тогда его объем равен сумме объема сегмента 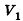
Случай, когда высота Н больше или равна R, рассмотрите самостоятельно.
Теорема доказана.
Определение:
Шаровым слоем (поясом) называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Расстояние между этими плоскостями называется высотой шарового слоя, а сечения, ограничивающие слой,— основаниями шарового слоя (рис. 217).
Заметим, что объем шарового слоя можно вычислить двумя способами:
- как разность объемов двух шаровых сегментов;
- как разность объема шара и объемов двух сегментов, не входящих в слой.
Объемы подобных тел
Из повседневного опыта нам хорошо известно, что при увеличении размеров предмета его объем также увеличивается. Например, легко сравнить объемы двух аквариумов, размеры одного из которых вдвое меньше соответствующих размеров другого (рис. 218): объемы отличаются в 8 раз.
Кроме того, можно проследить за подобными с коэффициентом k многоугольниками на плоскости. Как известно, их периметры отличаются в k раз, площади — в k2 раз. Естественно предположить, что объемы подобных с коэффициентом k пространственных тел отличаются к3 раз. Проверим это для тел, формулы объема которых нам уже известны.
Итак, для всех рассмотренных тел верно следующее утверждение: объемы тел, подобных с коэффициентом k, относятся как k3.
Этот факт верен и для любых простых тел, то есть тел, которые можно разбить на конечное число треугольных пирамид. В частности, любые многогранники, подобные с коэффициентом к, имеют объемы, которые отличаются в k3 раз.
Пример №5
Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды?
Решение:
Пусть дана пирамида с вершиной S и высотой SO. Плоскость, параллельная основанию пирамиды, пересекает SO в точке 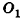
По условию = 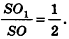
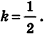
Ответ: 1:7.
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
В каждом конкретном случае используют разные методы. Все зависит от того, что нам известно (какие входные данные) и какая точность нам нужна.
Если возможно, то разбивают фигуру на более простые тела, объем которых можно посчитать: параллелепипед, цилиндр, эллипсоид и т.п. Объемы простых фигур складывают.
Если известна функция, которая описывает ограничивающую поверхность, то считают тройной интеграл.
Если аналитические методы не подходят или очень сложные, то можно изготовить такое тело, например, из гипса и бросить в воду. Объем вытесненной воды будет равен объему тела.
Есть и косвенные методы измерения.
Если известна масса тела и материал, из которого оно сделано, то можно вычислить объем по плотности материала.
Это не полный список методов. Наверняка, можно найти другие.
Как узнать объем фигуры. Как рассчитать объем емкости различной формы
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Инструкция
Узнайте плотность (ρ) материала, составляющего физическое тело, объем которого нужно рассчитать. Плотность — одна из двух характеристик объекта, задействованных в формуле вычисления объема. Если речь идет о реальных объектах, в расчетах используется средняя плотность, так как абсолютно физическое тело в реальных условиях представить трудно. В нем обязательно будут неравномерно распределенные хотя бы микроскопические пустоты или вкрапления посторонних материалов. Учитывайте при определении этого параметра и — чем она выше, тем меньше плотность вещества, так как при расстояние между его .
Второй параметр, который нужен для вычисления объема — масса (m) рассматриваемого тела. Эта величина определятся, как правило, по результатам взаимодействия объекта с другими или создаваемыми ими гравитационными полями. Чаще всего приходится иметь дело с массой, выраженной через взаимодействие с силой притяжения Земли — весом тела. Способы определения этой величины для относительно небольших объектов просты — их нужно просто взвесить.
Для вычисления объема (V) тела разделите определенный на втором шаге параметр — массу — на параметр, полученный на первом шаге — плотность: V=m/ρ.
В практических расчетах для вычислений можно использовать, например, объема. Он удобен тем, что не требует искать где-то еще плотность нужного материала и вводить его в вычислитель — в форме есть выпадающий с перечнем наиболее часто используемых в расчетах материалов. Выбрав в нем нужную строку, введите в поле «Масса» вес, а в поле «Точность вычисления» задайте количество знаков после запятой, которые должны присутствовать в результате вычислений.
Объем в и вы найдете в помещенной ниже таблице. Там же на всякий случай будут приведены радиус сферы и сторона куба, который должен соответствовать такой объем выбранного вещества.
Источники:
- Калькулятор объема
- объем формула физика
Существуют геометрические объемные фигуры, их объем легко вычислить по формулам. Гораздо более сложной задачей представляется вычисление объема тела
человека, но и ее можно решить практическим путем.
Вам понадобится
- — ванна
- — вода
- — карандаш
- — помощник
Измерьте все необходимые расстояния в метрах.
Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
- 1 мм = 0,001 м
- 1 см = 0,01 м
- 1 км = 1000 м
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу:
объем = L × W × H
(длину умножить на ширину умножить на высоту).
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5
- = 12 × 2,5
- = 30. Объем этой комнаты равен 30 м 3
.
- Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L 3 (или W 3 , или H 3).
Для вычисления объема фигур в виде цилиндра используйте формулу:
пи
× R 2 × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус — расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
- (3,14) × 0,75 2 × 10
- = (3,14) × 0,5625 × 10
- = 17,66. Объем колодца равен 17,66 м 3
.
Для вычисления объема шара используйте формулу:
4/3 х пи
× R 3 . То есть вам нужно знать только радиус (R) шара.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
- 4/3 х пи × (5) 3
- = 4/3 х (3,14) × 125
- = 4,189 × 125
- = 523,6. Объем воздушного шара равен 523,6 м 3
.
Для вычисления объема фигур в виде конуса используйте формулу:
1/3 х пи
× R 2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см.
Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
- 1/3 х (3,14) × 0,03 2 × 0,15
- = 1/3 х (3,14) × 0.0009 × 0,15
- = 1/3 × 0.0004239
- = 0,000141. Объем конуса мороженного равен 0,000141 м 3
.
Для вычисления объема фигур неправильной формы используйте несколько формул.
Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
- пи × R 2 × H + 1/3 х пи × R 2 × H
- (3,14) × 1,5 2 × 12 + 1/3 х (3,14) × 1,5 2 × 1
- = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
- = (3,14) × 27 + 1/3 х (3,14) × 2,25
- = 84,822 + 2,356
- = 87,178.
Объем зернохранилища равен 87,178 м 3
.
Для устройства фундамента, возведения стен и заливки пола применяются бетонные растворы. До начала мероприятий важно выбрать конструкцию фундаментного основания, правильно рассчитать общий уровень затрат и определить необходимое количество строительных материалов. Зная, как рассчитать объем бетона, можно определить сметную стоимость строительных мероприятий, точно спланировать продолжительность выполнения бетонных работ и избежать непредвиденных затрат. Остановимся детально на методике выполнения расчетов для различных , а также стен и пола.
Схема ленточного фундамента
Какими методами можно рассчитать объем бетона
Выполнению строительных работ предшествует разработка проекта. На этом этапе определяется вид фундаментной базы, и рассчитывается требуемый для возведения основания объем бетонного раствора. На проектной стадии вычисляется потребность в растворе для заливки монолитных стен и бетонного пола.
Определение кубатуры бетонной смеси, необходимой для выполнения работ, производится по объему бетонируемых конструкций здания.
Для выполнения расчетов используются различные методы
:
- ручной. Он базируется на вычислении объемов фундаментного основания, капитальных стен и пола. Расчет производится на обычном калькуляторе по школьным формулам вычисления объема и не учитывает коэффициент усадки бетона. Полученное значение незначительно отличается от результатов вычислений с помощью программных средств;
- программный. Введенные в программу исходные данные о типе фундаментной основы, ее габаритах, конструктивных особенностях и марке бетона оперативно обрабатываются. В результате выдается довольно точный результат, на который можно ориентироваться, приобретая стройматериал для сооружения фундаментной базы, постройки стен или заливки пола.
Особенности при вычислении объема бетона
Для получения точного результата недостаточно учитывать только внутренний размер опалубки.
Второй способ более точен, так как онлайн-калькулятор учитывает все данные: тип фундамента, сечение фундаментной базы, наличие арматурного каркаса и марку раствора.
Готовимся определить объем бетона – как посчитать без ошибок
Готовясь к выполнению расчетов, следует запомнить, что потребность в бетонной смеси определяется в кубометрах, а не в килограммах, тоннах или литрах. В результате ручных или программных расчетов будет определен объем связующего раствора, а не его масса. Одна из главных ошибок, которую допускают начинающие застройщики – выполнение расчетов до того, как будет определен тип фундаментной основы.
Решение о конструкции фундамента принимается после выполнения следующих работ
:
- производства геодезических мероприятий, позволяющих определить свойства грунта, уровень замерзания и расположение водоносных жил;
- вычисления нагрузочной способности базы. Она определяется на основании веса, конструктивных особенностей строения и природных факторов.
Как рассчитать количество (объем) бетонной смеси
- разновидность сооружаемой основы;
- габариты фундамента, его конфигурацию;
- марку смеси, применяемую для бетонирования;
- глубину промерзания грунта.
Точность, с которой посчитан объем бетона, зависит от используемых для расчета данных.
Они разные для каждого типа фундамента
:
- при расчете ленточного основания учитываются его габариты и форма;
- для столбчатой основы важно знать количество бетонных колонн и их размеры;
- рассчитать куб бетона для цельной плиты можно по ее толщине и размерам.
От полноты используемых для расчета данных зависит точность полученного результата.
Как рассчитать бетон в кубах для фундаментной основы
Для всех типов оснований потребность в бетоне определяется по формуле, учитывающей суммарный объем возводимых фундаментных конструкций. При этом в обязательном порядке учитывается и часть фундамента, заливаемая в грунт.
- столбчатого;
- ростверкового.
Определение потребности в бетонном растворе для каждого вида фундаментной основы имеет свои особенности.
Как высчитать куб бетона для ленточной базы
Калькулятор ленточного фундамента
Основание ленточного типа достаточно популярно. Оно используется для строительства частных домов, хозяйственных построек и дачных строений. Конструкция представляет собой цельную ленту из бетона, армированную стальными прутками. Монолитная лента повторяет контур строения, включая внутренние перегородки.
Таблица состава и пропорций бетонной смеси
Расчет объема бетона для монолитного ленточного фундамента производится по простой формуле V = AхBхP. Расшифруем ее
:
- V – потребность в бетонном растворе, выраженная в кубических метрах;
- A – толщина фундаментной ленты;
- B – высота ленточные базы, включая подземную часть;
- P – периметр формируемого ленточного контура.
Перемножив между собой данные параметры, вычислим суммарную кубатуру бетонного раствора.
Рассмотрим алгоритм вычислений для ленточного основания с размерами 6х8 м, толщиной 0,5 м и высотой 1,2 м. Выполняйте расчет по следующему алгоритму
:
- Рассчитайте периметр, удвоив длину сторон 2х(6+8)=28 м.
- Вычислите площадь сечения, перемножив толщину и высоту ленты 0,5х1,2=0,6 м 2 .
- Определите объем, перемножив периметр на площадь сечения 28х0,6=16,8 м 3 .
Полученный результат имеет небольшую погрешность, связанную с тем, что не учитывается железобетонная арматура и усадка смеси во время вибрационного уплотнения.
Схема ленточного фундамента
Как вычислить куб бетона для основания свайного типа
Основание в виде бетонных колонн является одним из наиболее простых. Оно представляет собой железобетонные опоры, равномерно расположенные по контуру здания, в том числе по углам строения, а также в местах пересечения внутренних перегородок со стенами.
Для вычислений используйте формулу – V=Sхn, которая расшифровывается следующим образом
:
- V – количество раствора для заливки колонн;
- S – площадь поперечного сечения опорного элемента;
- n – суммарное количество свайных колонн.
На примере требований проекта, предусматривающего установку 40 свай диаметром 0,3 м и общей длиной 1,8 м, вычисляем требуемое количество бетона
:
- Рассчитайте площадь сваи, умножив коэффициент 3,14 на квадрат радиуса — 3,14х0,15х0,15=0,07065 м 2 .
- Вычислите объем одной опоры, умножив ее площадь на длину — 0,07065х1,8=0,127 м 3 .
- Определите необходимые количество смеси, перемножив объем одной сваи на общее количество опор 0,127х40=5,08 м 3 .
Как рассчитать куб бетона
При прямоугольном сечении опорных колонн, для расчета поперечного сечения необходимо перемножить ширину и толщину элемента.

Как посчитать бетон для столбчатой основы с железобетонным ростверком
Для повышения прочностных характеристик столбчатой основы выступающие части опор объединяют железобетонной конструкцией, которая называется ростверком. Он выполняется в виде цельной железобетонной ленты или плиты, в которой забетонированы оголовки колонн.
Как рассчитать объем бетона для строительства ленточного фундамента и свай
- Определить площадь сечения ростверка, умножив его толщину на высоту;
- Рассчитать объем ростверка, перемножив площадь сечения на длину конструкции.
Полученное значение соответствует потребности в бетонной смеси для бетонирования ростверковой основы.
Вычисляем объем бетона для фундамента в виде цельной плиты
Основание плитного типа применяется на сложных грунтах с повышенной концентрацией влаги. На нем возводят здания без подвального помещения. Эта конструкция позволяет равномерно распределить нагрузку от массы строения на почву и обеспечить повышенную жесткость и устойчивость возводимого объекта.
Как рассчитать объем бетона
Расшифровка обозначений
:
- V – объем бетонного состава для заливки плиты;
- S – площадь плитной основы в поперечном сечении;
- L – длина фундаментной конструкции.
Для фундамента длиной 12 м, шириной 10 м и толщиной 0,5 м рассмотрим алгоритм вычислений
:
- Определите площадь, перемножив ширину плиты на ее толщину 10х0,5=5 м 2 .
- Вычислите объем основы, умножив длину конструкции на площадь 12х5=60 м 3 .
Полученное значение соответствует потребности в бетонной смеси. Если плитный фундамент имеет сложную конфигурацию, то его следует разбить на плане на более простые фигуры, а затем вычислить для каждой площадь и объем.
Как правильно рассчитать куб бетона для возведения стен
Калькулятор расчета количества бетона на ленточный фундамент на сайте
Для постройки массивных зданий сооружают прочные коробки из бетона, усиленного стальной арматурой.
Расшифруем входящие в формулу обозначения
:
- V – количество бетонной смеси для возведения стен;
- S – общая площадь стенной поверхности;
- S1 – суммарная площадь оконных и дверных проемов;
- H – высота бетонируемой стенной коробки.
При выполнении расчетов общая площадь проемов определяется путем суммирования отдельных проемов. Алгоритм расчета напоминает определение потребности в бетоне для плитного основания и легко может быть выполнен самостоятельно с использованием калькулятора.
Как посчитать куб бетона для заливки пола
Как рассчитать объем бетона для пола
Для повышения нагрузочной способности пола и обеспечения его плоскостности выполняется бетонная стяжка. После застывания бетона такая поверхность служит основой для укладки напольных покрытий или керамической плитки.
Формула для определения количества раствора V=Sxh расшифровывается легко
:
- V – количество заливаемого материала;
- S – суммарная площадь бетонируемой стяжки;
- h – толщина бетонной основы.
Разберемся, как выполнить вычисления для помещения с размерами 6х8 м и толщиной бетонной основы 0,06 м
:
- Определите площадь напольной поверхности, перемножив длину и ширину помещения – 6х8=48 м 2 .
- Вычислите объем заливаемого бетонного состава для формирования стяжки, умножив площадь на толщину слоя – 48х0,06=2,88 м 3 .
Руководствуясь приведенным алгоритмом, можно легко определить количество бетонного состава для бетонирования пола.
Возникают ситуации, когда черновая поверхность имеет уклон. В этом случае формируемая стяжка имеет разную толщину по площади помещения. В данной ситуации можно использовать усредненную толщину слоя, что снижает точность вычислений.
Заключение – для чего необходимо знать, как рассчитать куб бетона
Занимаясь строительством и планируя самостоятельно изготавливать бетонный раствор или приобретать его на предприятиях железобетонных изделий в необходимом количестве, важно знать, как рассчитать объем бетона. Это позволит спрогнозировать сумму предстоящих расходов, своевременно приобрести стройматериалы, и выполнить работы в запланированные сроки. Произвести расчеты можно как вручную на калькуляторе, так и с помощью программных средств. Главное – овладеть методикой вычислений и использовать для определения количества бетона достоверные данные.
Все величины указываем в мм
H
— Уровень жидкости.
Y
— Резервуар в высоту.
L
— Длина емкости.
X
— Резервуар в ширину.
Данная программа выполняет вычисления объема жидкости в различных по размеру емкостях прямоугольной формы, также поможет рассчитать площадь поверхности резервуара, свободный и общий объем.
По итогам вычисления Вы узнаете:
- Полную площадь резервуара;
- Площадь боковой поверхности;
- Площадь дна;
- Свободный объем;
- Количество жидкости;
- Объем емкости.
Технология расчета количества жидкости в резервуарах разной формы
Когда емкость неправильной геометрической формы (к примеру, в виде пирамиды, параллелепипеда, прямоугольника и т.д.) необходимо в первую очередь выполнить измерения внутренних линейных размеров и только после этого произвести вычисления.
Расчет объема жидкости в прямоугольной емкости небольших размеров, вручную можно выполнить следующим образом. Необходимо залить жидкостью весь резервуар до краев. Тогда объем воды в данном случае станет равен объему резервуара.
Если резервуар большого размера, и в ручную невозможно измерить количество жидкости, то можно использовать формулу массы газа с молярной известной массой. К примеру, масса азота М=0,028 кг/моль. Данные вычисления возможны, когда резервуар можно плотно закрыть (герметически). Теперь при помощи термометра измеряем температуру внутри резервуара, и манометром внутреннее давление. Температура должна быть выражена в Кельвинах, а давление в Паскалях. Вычислить объем внутреннего газа можно следующей формуле (V=(m∙R∙T)/(M∙P)). То есть массу газа (m) умножаем на температуру его (Т) и газовую константу (R).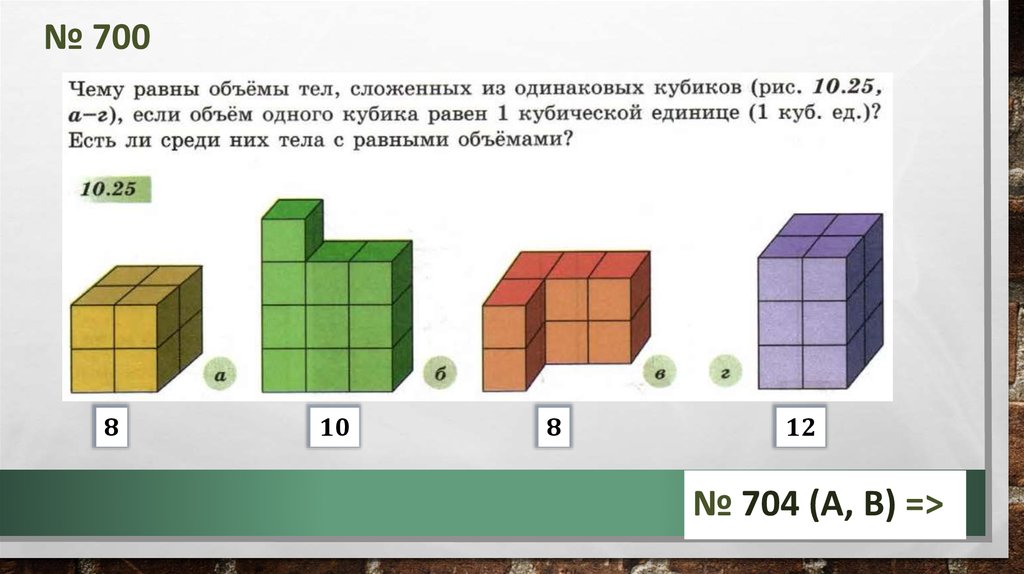
Как вычислить и узнать объем аквариума по размерам самостоятельно
Аквариумы – стеклянные сосуды, которые заполняют чистой водой до определенного уровня. Многие собственники аквариума неоднократно задумывались, какого объема их резервуар, как можно выполнить вычисления. Самый простой и надежный метод, это воспользоваться рулеткой и замерять все необходимые параметры, которые следует вбить в соответствующие ячейки нашего калькулятора, и Вы сразу же получите готовый результат.
Однако существует и другой способ определения объема аквариума, который заключается в более долгом процессе, использования литровой банки, постепенно заполняя всю емкость до соответствующего уровня.
Третий метод вычисления объема аквариума, это специальная формула. Замеряем глубину резервуара, высоту и ширину в сантиметрах. К примеру, у нас получились следующие параметры: глубина – 50 см, высота – 60 см и ширина – 100 см.
Каждый аквариум наполняют значительно ниже, чем его реальная высота, дабы избежать перелива воды, чтобы закрыть крышкой с учетом стяжки. К примеру, когда наш аквариум высотой 60 сантиметров, тогда вклеенные стяжки будут располагаться на 3-5 сантиметров ниже. При нашем размере в 60 сантиметров, чуть менее 10% объема емкости припадает на 5-сантиметровые стяжки. Отсюда мы можем вычислить реальный объем 300 л – 10%=270 л.
Важно! Следует отнять несколько процентов учитывая объем стекол, размеры аквариума или любой другой емкости снимаем с наружной стороны (без учета толщины стекол).

Отсюда объем нашего резервуара будет равен 260 литров.
Расчет объема фигур. Как вычислить объем тела неправильной формы. Объемные геометрические фигуры
– бесплатный геометрический калькулятор поможет вам в два клика подсчитать площадь или объем относительно простых геометрических фигур. Не нужно заниматься поиском нужных формул и производить расчеты на листочке. Работа с программой очень проста, для начала нужно выбрать, что нужно подсчитать: площадь фигуры, площадь полной поверхности или же объем. Выбранная фигура отображается рядом в окошке, и рядом с ней будет показана формула для подсчета искомой величины. Изначально все результаты округляются до целой части, но есть возможность изменить и выбрать необходимую точность, с которой следует выводить результаты. Для этого доступны варианты от одного до десяти знаков после запятой.
Что можно рассчитать?
- Круг – находим длину окружности по известному радиусу, и диаметр по известной окружности.
- Находим площадь – круга, сектора круга, элипса, квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, тора.
- Площадь поверхности – куба, призмы, пирамиды, цилиндра, сферы, конуса, тора.
- Объём фигур – куб, кубоид, призма, пирамида, цилиндр, сферы, конуса, тор, усечённый конус, бочка.
Убедитесь, что тело является водонепроницаемым, так как описанный метод подразумевает погружение тела в воду.
Если тело полое или в него может проникнуть вода, то вы не сможете точно определить его объем, используя этот метод. Если тело поглощает воду, убедитесь, что вода не повредит его. Не погружайте в воду электрические или электронные предметы, так как это может привести к поражению электрическим током и/или к повреждению самого предмета.
- Если возможно, запечатайте тело в водонепроницаемый пластиковый пакет (предварительно выпустив из него воздух). В этом случае вы вычислите довольно точное значение объема тела, так как объем пластикового пакета, скорее всего, будет небольшим (по сравнению с объемом тела).
Найдите емкость, в которой помещается тело, объем которого вы вычисляете.
Если вы измеряете объем небольшого предмета, воспользуйтесь мерным стаканом с нанесенной градуировкой (шкалой) объема. В противном случае найдите емкость, объем которой можно легко вычислить, например, емкость в форме прямоугольного параллелепипеда, куба или цилиндра (стакан тоже можно рассматривать как емкость цилиндрической формы).
- Возьмите сухое полотенце, чтобы положить на него тело, вытащенное из воды.
Наполните емкость водой так, чтобы в нее можно было полностью погрузить тело, но при этом оставьте достаточно места между поверхностью воды и верхней кромкой емкости.
Если основание тела имеет неправильную форму, например, закругленные нижние углы, заполните емкость так, чтобы поверхность воды достигала часть тела правильной формы, например, прямые прямоугольные стенки.
Отметьте уровень воды.
Если емкость с водой прозрачная, отметьте ее уровень с внешней стороны емкости при помощи водостойкого маркера.
Погрузите тело полностью в воду.
Если оно поглощает воду, подождите по крайней мере тридцать секунд, а затем вытащите тело из воды. Уровень воды должен опуститься, так как часть воды находится в теле. Удалите отметки (маркер или клейкую ленту) о предыдущем уровне воды и отметьте новый уровень. Затем еще раз погрузите тело в воду и оставьте его там.
Если тело плавает, прикрепите к нему тяжелый предмет (в качестве грузила) и продолжите вычисления с ним.
После этого повторите вычисления исключительно с грузилом, чтобы найти его объем. Затем вычтите объем грузила из объема тела с прикрепленным грузилом и вы найдете объем тела.
- При вычислении объема грузила прикрепите к нему то, чем вы крепили грузило к рассматриваемому телу (например, ленту или булавки).
Отметьте уровень воды с погруженным в нее телом.
Если вы используете мерный стакан, запишите уровень воды согласно шкале на стакане.
Знайте, почему этот метод работает.
Изменение объема воды равно объему тела неправильной формы. Способ измерения объема тела с помощью емкости с водой основан на том, что при погружении тела в жидкость объем жидкости с погруженным в нее телом увеличивается на величину объема тела (то есть тело вытесняет объем воды, равный объему этого тела). В зависимости от формы используемой емкости с водой существуют различные способы вычисления объема вытесненной воды, который равен объему тела.
Найдите объем, используя мерную шкалу стакана.
Если вы использовали емкость с мерной шкалой, то у вас уже должны быть записаны два значения уровня воды (ее объема). В этом случае из значения объема воды с погруженным в нее телом вычтите значение объема воды до погружения тела. Вы получите объем тела.
Найдите объем, используя емкость прямоугольной формы.
Если вы использовали емкость в форме прямоугольного параллелепипеда, измерьте расстояние между двумя метками (уровень воды до погружения тела и уровень воды после погружения тела), а также длину и ширину емкости с водой. Объем вытесненной воды найдите посредством перемножения длины и ширины емкости, а также расстояния между двумя метками (то есть вы вычисляете объем небольшого прямоугольного параллелепипеда). Вы получите объем тела.
- Не измеряйте высоту емкости с водой. Измерьте только расстояние между двумя метками.
- Используйте
Геометрические фигуры — это замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом линий. Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Любое тело, имеющее форму, представляет собой совокупность геометрических фигур.
Любую фигуру можно описать математической формулой различной степени сложности.
Основными математическими параметрами геометрических фигур являются радиусы, длины сторон или граней и углы между ними.
Ниже представлены основные геометрические фигуры, наиболее часто используемые в прикладных расчетах, формулы и ссылки на расчетные программы.
Линейные геометрические фигуры
1. Точка
Точка — это базовый объект измерения. Основной и единственной математической характеристикой точки является её координата.
2. Линия
Линия — это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек. Основной математической характеристикой линии является длина.
Луч — это тонкий пространственный объект имеющий бесконечную длину и представляющий собой цепь связанных друг с другом точек. Основными математическими характеристиками луча являются координата его начала и направление.
Плоские геометрические фигуры
1. Круг
Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.
2. Квадрат
Квадрат — это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.
3. Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.
4. Треугольник
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.
5. Трапеция
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.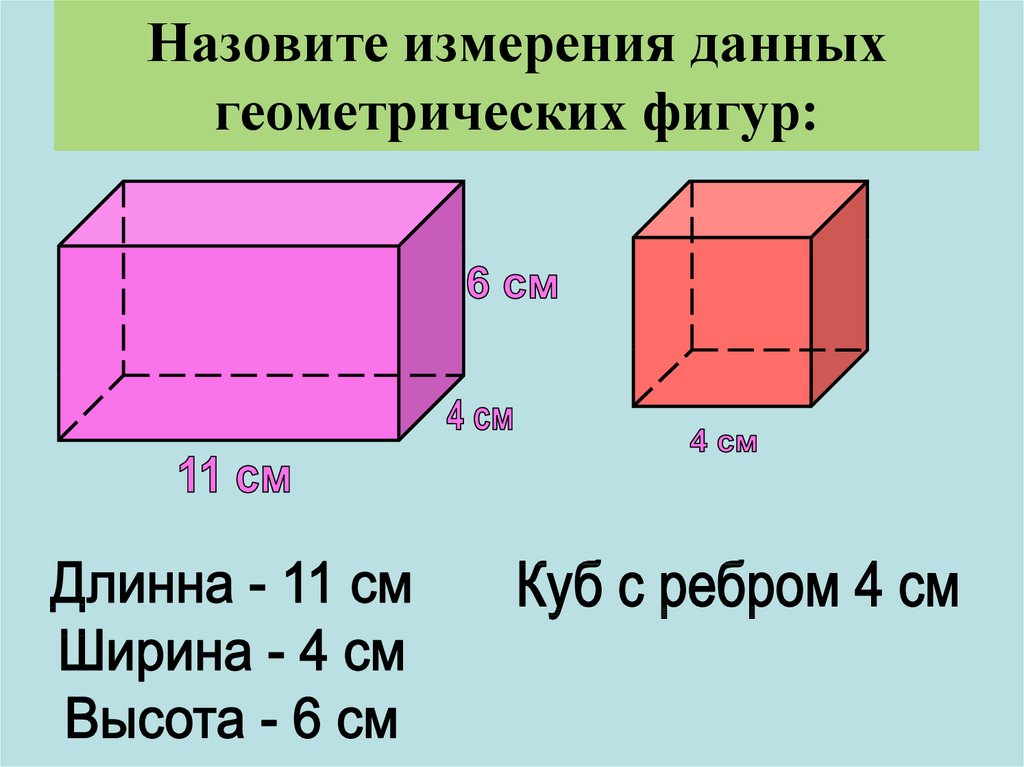
6. Параллелограмм
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.
Ромб — это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам. Основными математическими характеристиками ромба являются длина его стороны и высота.
8. Эллипс
Эллипс — это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.
Объемные геометрические фигуры
1. Шар
Шар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.
Сфера — это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Куб — это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат. Основной математической характеристикой куба является длина его ребра.
4. Параллелепипед
Параллелепипед — это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
5. Призма
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.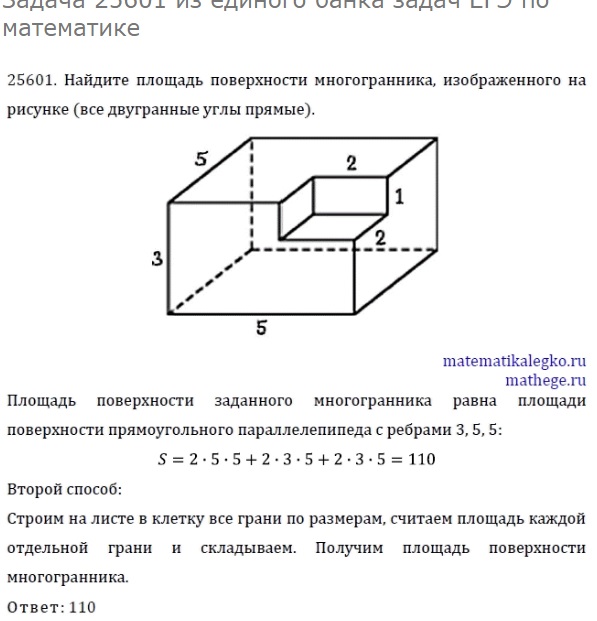
Конус — это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.
7. Пирамида
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
8. Цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.
Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.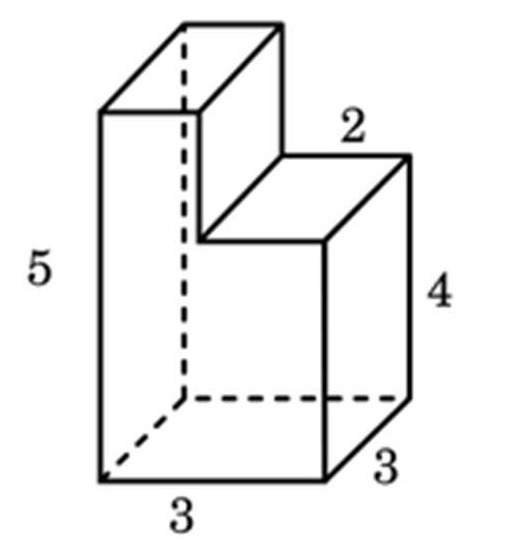
Формула объема
необходима для вычисления параметров и характеристик геометрической фигуры.
Объем фигуры
— это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
| Фигура | Формула | Чертеж |
|---|---|---|
|
Параллелепипед Объем прямоугольного параллелепипеда |
||
|
Цилиндр Объем цилиндра равен произведению площади основания на высоту. Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту. |
||
|
Пирамида Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS). |
||
|
Правильная пирамида |
||
|
Правильная треугольная пирамида |
||
|
Правильная четырехугольная пирамида |
||
|
Тетраэдр |
V = (a 3 √2)/12 |
|
|
Усеченная пирамида Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S 1 (abcde), нижнего основания усеченной пирамиды S 2 (ABCDE) и средней пропорциональной между ними. |
V= 1/3 h (S 1 + √S 1 S 2 + S 2) |
|
|
Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 . |
||
|
Конус |
||
|
Усеченный конус |
V = 1/3 πh (R 2 + Rr + r 2) |
|
|
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра. |
||
|
Призма Объем призмы равен произведению площади основания призмы, на высоту. |
Объемы геометрических фигур.
Расчет площади и объема в AutoCAD
Как в Автокаде посчитать площадь
Знать площадь фигуры в Автокаде на разных этапах работы является необходимым условием создания проекта. Поэтому в этой статье рассмотрим, как в Автокаде измерить площадь, а также затронем основные нюансы, связанные с этим вопросом.
В первую очередь, советую ознакомиться с видео-материалом, в котором я рассматриваю специфический, но в то же время самый рациональный способ определения/измерения площади для объектов любой формы. Суть данного подхода, лежит в том, чтобы определить площадь штриховки в Автокаде, которая и будет соответствовать искомому параметру для нужного контура.
Как найти площадь в Автокаде стандартным способом?
Определить площадь в Автокаде можно с помощью стандартного инструмента, который расположен на вкладке «Главная» — панель «Утилиты» — вниз спадающий список «Измерить» — команда «Площадь» (см.
Инструмент площадь AutoCAD
Итак, после выбора команды следует указать точки по периметру фигуру. Значение площади отобразится в Журнале командной строки. Там же появится и периметр объекта. Не пугайтесь столь большим значениям. Все дело в том, что площадь отображается в мм2. Немного позже рассмотрим, как ее переводить в м2.
Тут особый интерес представляют субопции команды «Площадь»:
- оБъекты— для отображения площади нужно указать контур замкнутой фигуры;
- Добавить площадь— позволяет подсчитывать площадь сразу нескольких объектов. Для этого, нужно активировать данную субопцию, после чего здесь же обратиться к параметру «объекты» и в графическом поле выбрать замкнутые фигуры в нужном количестве.
ПРИМЕЧАНИЕ:
Читайте про то, как в AutoCAD объединить объекты в цельные 2D примитивы.
- Вычесть площадь— действие противоположное. Позволяет убрать объекты из ранее выбранных для подсчета общей площади.
Как изменить единицы измерения площади в AutoCAD/Автокад?
Итак, как в Автокаде померить площадь мы уже знаем, однако, значения отображаются в мм2 и это не очень удобно. Для того чтобы перевести их в привычные для нас м2, воспользуемся быстрым калькулятором. Для этого достаточно в свободном месте графического пространства нажать ПКМ и выбрать «БыстрКальк» (см. рис.).
Вызов Быстрого калькулятора AutoCAD
Журнал командной строки можно несколько увеличить путем растягивания его границ с помощью мышки. Далее находим нужное значение площади/периметра, копируем его (Ctrl+C) и вставляем значение в калькулятор.
Работа с быстрым калькулятором в AutoCAD
Нажав на знак «+» возле «Преобразование единиц» нужно установить «Тип единиц», выбрав из списка «Площадь», а также изменить значение поля «Преобразовать из» на «Квадратные миллиметры». Чтобы преобразуемое значения отобразилось в соответствующем поле, достаточно просто щелкнуть ЛКМ внутри этого поля (см. рис.).
Преобразование единиц с помощью быстрого калькулятора AutoCAD
Как видите, при таком подходе преобразование единиц площади из мм2 в м2выполняется автоматически.
Как узнать площадь в Автокаде через свойства объекта?
На самом деле, подсчет площади в Автокаде выполняется автоматически и для стандартных замкнутых примитивов, таких как окружности, прямоугольники или, что намного интереснее, полилинии, создающей контур, данное значение можно посмотреть в палитре «Свойства» (горячая клавиша Ctrl+1).
ПРИМЕЧАНИЕ:
Преобразование единиц площади из мм2 в м2 можно осуществлять путем вызова быстрого калькулятора, нажав на соответствующую кнопку в поле «Площадь» (см. рис.). Сам принцип аналогичен вышеописанному.
Значение площади для замкнутого объекта в AutoCAD
Площадь в Автокаде 2013 и 2015. Есть разница?
Как рассказывалось ранее, существенных изменений программа претерпела начиная с 2009 версии. Поэтому площадь в Автокаде 2012-2015 версии, также как и 2009-2010, определяется по одному и тому же принципу, описанному выше.
Как видите, простейшие расчеты в Автокаде выполняются автоматически, а их значения можно посмотреть в свойствах объекта. Теперь вы знаете, как определить площадь в Автокаде и преобразовать это значение в удобные для вас единицы измерения.
Как посчитать объем в Автокаде
В Автокаде зачастую нужно измерить различные параметры объектов на этапе создания проекта. Стандартные команды измерения основных характеристик расположены на вкладке «Главная», панель «Утилиты». Так, подсчет объемов в Автокаде можно выполнить с помощью команды «Объем» (см. рис.).
Объем в Автокаде
Итак, последовательность действий определения объема выполняется аналогично вычислению площади объектов Опишем данную процедуру вкратце: после активации команды следует в командной строке выбрать субопцию «Объект». Если нужно рассчитать данный параметр сразу для нескольких тел, то воспользуйтесь субопцией «Добавить объем» после чего обратитесь к параметру «Объект» и укажите на чертеже нужные элементы (см. рис.).
Объем фигуры в Автокаде
Про то, как считать объемы в Автокаде ясно, но вот значение, которое отображается в командной строке имеет единицы измерения мм3, а это не удобно.
ПРИМЕЧАНИЕ:
Что бы развернуть Журнал командной строки для просмотра полученного значения объема, после выполнения соответствующей команды, можете воспользоваться горячей клавишей F2.
Объем в Автокаде с помощью команды МАСС-ХАР
Объем в AutocCAD также можно рассчитать, воспользовавшись командой «МАСС-ХАР», обладающей намного большим функционалом. К тому же, все характеристики, которые будут получены, можно сохранить в отдельный текстовый файл (см. рис.).
Для выполнения команды, пропишите ее название в командной строке, затем выберите нужные объекты AutoCAD, объем 3d тела которого следует определить, после чего нажмите Enter. Команда выполнится. Чтоб записать результаты анализа в файл нажмите еще раз Enter и обратитесь к ключевому слову «Да» в командной строке (см.
Объем тела в Автокаде (команда МАСС-ХАР)
Что ж, теперь вы знаете несколько способов, как считать объем в Автокаде. Уверен, что рано или поздно, вам этот материал пригодится.
Автоматизированная оценка теста комплексной фигуры Рея-Остеррита с использованием алгоритма глубокого обучения | Архив клинической нейропсихологии
Фильтр поиска панели навигации
Архивы клинической нейропсихологииЭтот выпускНейропсихологияНейронаукаКнигиЖурналыOxford Academic
Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Архивы клинической нейропсихологииЭтот выпускНейропсихологияНейронаукаКнигиЖурналыOxford Academic
Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Дж Фогт,
Дж Фогт
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Х Клоостерман,
Х.
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
С Вермен,
S Vermeent
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Г Ван Эльсвейк,
Г Ван Эльсвейк
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Р Дотч,
Р Доч
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Б Шманд
Б Шманд
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Архив клинической нейропсихологии , том 34, выпуск 6, август 2019 г.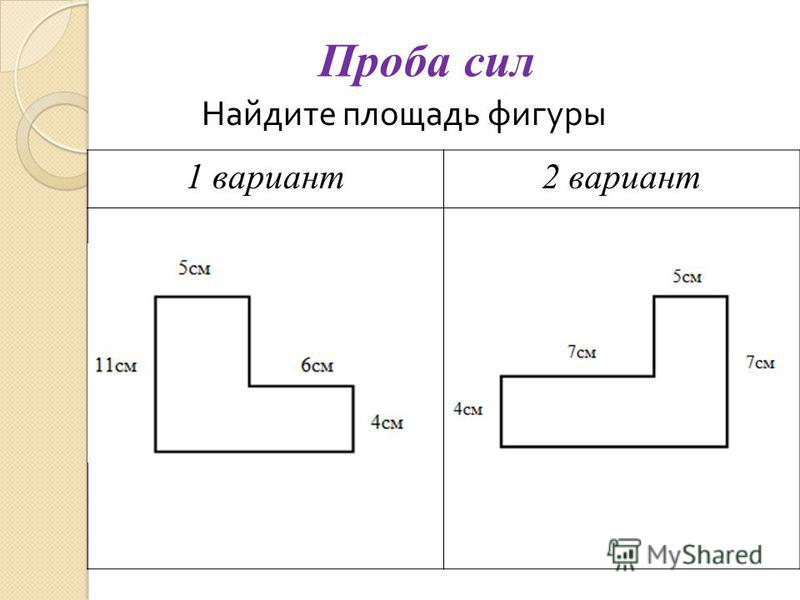
Опубликовано:
25 июля 2019 г.
История статьи
Получен:
21 января 2019 г.
Полученная ревизия:
07 марта 2019 г.
Ревизия.
PDF
- Содержание статьи
- Рисунки и таблицы
- видео
- Аудио
- Дополнительные данные
Цитировать
Cite
J Vogt, H Kloosterman, S Vermeent, G Van Elswijk, R Dotsch, B Schmand, Автоматическая оценка теста сложной фигуры Рея-Остеррита с использованием алгоритма глубокого обучения, Архив клинической нейропсихологии , том 34, выпуск 6, август 2019 г.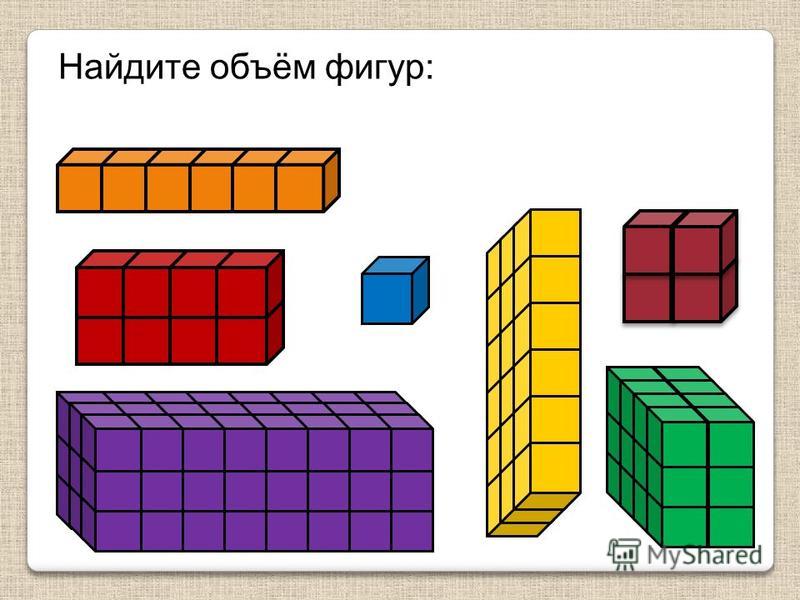
Выберите формат
Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Разрешения
- Электронная почта
- Твиттер
- Фейсбук
- Подробнее
Фильтр поиска панели навигации
Архивы клинической нейропсихологииЭтот выпускНейропсихологияНейронаукаКнигиЖурналыOxford Academic
Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Архивы клинической нейропсихологииЭтот выпускНейропсихологияНейронаукаКнигиЖурналыOxford Academic
Термин поиска на микросайте
Расширенный поиск
Цель
Проверить полностью автоматизированный алгоритм оценки для теста комплексной фигуры Рея-Остеррита (ROCFT) путем сравнения результатов оценки алгоритма с результатами оценщиков-людей.
Метод
Алгоритм состоял из каскада глубоких нейронных сетей, которые были обучены на оценках людей для извлечения 18 сегментов фигуры и количественной оценки показателей пациента. Результаты алгоритма сравнивались с шестью экспертами-оценщиками для 303 рисунков. Мы проверили, была ли средняя корреляция между оценками алгоритма и оценками всех людей-оценщиков эквивалентна средней корреляции между экспертами (с границей равенства Δr <0,05). Были использованы пробы немедленного и отсроченного отзыва; пробная копия показала сильный эффект потолка.
Результаты
Средняя корреляция Пирсона между оценщиками составила 0,94 (SD = 0,01). Корреляция между алгоритмом и оценщиками составила 0,88 (SD = 0,02). Тест эквивалентности двустороннего t-теста (TOST) показал, что эти корреляции не были строго эквивалентными, t (5) = 4,02, p = 0,995, 95% ДИ [0,35, 0,52].
Выводы
Хотя алгоритм не является строго эквивалентным человеческому рейтингу, производительность алгоритма высока, приближаясь к уровню надежности, характерному для людей-оценщиков.
Этот контент доступен только в формате PDF.
© Автор(ы), 2019. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
© Автор(ы), 2019. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
Раздел выпуска:
Текущие проблемы тестирования – технологии, усилия и мотивация-4
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
-
Последний
-
Самые читаемые
-
Самые цитируемые
Систематический обзор и латиноамериканская клиническая модель теленейропсихологической оценки
Оценка эффективности и осуществимости программы телереабилитации с использованием языка и когнитивных упражнений при многодоменном амнестическом легком когнитивном нарушении
Включение интерсекциональности в нейропсихологию: продвижение дисциплины вперед
Функциональные исходы, переменные травмы и характеристики спортсменов, связанные с нарушением сна после сотрясения мозга
Профиль встроенных показателей валидности у подсудимых по уголовным делам с подтвержденными результатами нейропсихологического теста
Реклама
Обзор объемных 3D-фигур
Площадь и объем сложного объекта
Площадь и объем сложных объектов
В этом уроке мы рассмотрим нахождение площади и объема предметов, которые
создаются либо путем соединения простых предметов, либо путем вырезания одного
простой объект от другого. Предполагается, что вы уже знакомы
с геометрическими формулами, связанными с прямоугольниками, кругами и
треугольники. Если вам нужен обзор этого, перейдите к
урок основных фигур.
Стратегия, которую мы будем использовать для нахождения площади этих сложных объектов, заключается в следующем:
следующий.
Стратегия нахождения площади сложных объектов
- Определите, образован ли объект путем объединения основных форм или путем
удаление базовой формы из другой базовой формы. - Найдите площадь каждой фигуры, определенной на шаге 1.
- Добавьте области, если объект сформирован путем объединения этих основных
формы или вычесть области, если объект сформирован путем удаления основного
форма из другой базовой формы.
Пример 1
Найдите площадь фигуры, показанной ниже
Раствор
- Мы можем реализовать это как три прямоугольника, склеенных вместе. Есть
более чем один способ сделать это. (Обратите внимание, что другой подход заключается в удалении
два прямоугольника из большего прямоугольника). Ниже приведен один из способов резки
этот прямоугольник на три части. - Обратите внимание, что мы смогли найти ширину прямоугольника C, увидев
что это длинная ширина 7 минус
короткая ширина 2 минус еще одна короткая ширина
2:7 — 2 — 2 =
3Также обратите внимание, что ширина прямоугольника A равна 5
так как мы вырезали правую часть «B» длиной
2 с длинной стороны длины
7.Теперь найдем площади каждого прямоугольника. Напомним, что площадь
прямоугольника это длина умноженная на ширину.Площадь прямоугольника A
= (4)(5) = 20Площадь прямоугольника B = (2)(2) = 4
Площадь прямоугольника C = (1)(3) = 3
- Суммируем три площади, чтобы найти общую площадь.
Общая площадь = площадь A +
Площадь B + Площадь C= 20 + 4 + 3 = 27
Итак, общая площадь равна 27 кв.
единицы.
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку
на желтом прямоугольнике и появится ответ.
Упражнение 1
Найдите площадь области, показанной ниже. (Подсказка: площадь
прямоугольный треугольник с основанием b и высотой
h равно A = 1/2 bh).
Ответить
Пример 2
Квадрат со стороной 7 находится внутри
круг диаметром 10. Найдите площадь части круга, не содержащей
площадь.
Раствор
- Обратите внимание, что мы «отнимаем квадрат от круга».
На приведенной ниже диаграмме показаны две фигуры, нарисованные отдельно. - Теперь найдем площадь двух областей. Формула площади
кругаПлощадь круга = pr 2
≈
3,14 р 2Нам не дан радиус напрямую, но нам дан диаметр.
Напомним, что радиус равен половине знаменателя.г = (1/2)(10) = 5
это дает нам
Площадь круга = 3,14(25)
= (3.14)(25)
= 78,5
Находим площадь квадрата, возводим длину стороны в квадрат
Площадь квадрата = 7 2 = 49
- Наконец, мы готовы найти площадь
затененный в регионе. Эта площадь равна площади круга минус
площадь площади.
Общая площадь = площадь круга — площадь квадрата= 78,5 — 49 = 29,5
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку
на желтом прямоугольнике и появится ответ.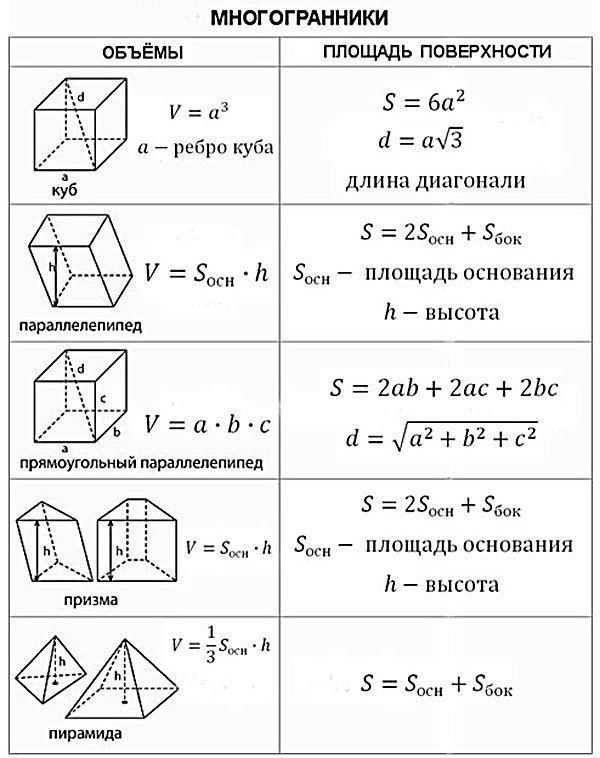
Упражнение 2
Окружность радиусом 2,8 удалена из
показанный ниже треугольник. Найдите оставшуюся площадь. (Округлите ответ до
один десятичный знак.
Ответить
Объем
Мы будем использовать аналогичную стратегию для нахождения объемов трехмерных фигур.
Вот шаги, чтобы найти такие объемы.
Этапы нахождения объема сложных твердых тел
- Определите части, из которых состоит твердое тело.
- Найдите объем каждой части.
- Сложите тома, чтобы получить общий объем.
Пример 3
Здание построено из цилиндрической банки высотой
20 футов и базовый радиус 10
ноги с полусферическим телом, как показано на рисунке ниже. Найди
приблизительный объем этого здания. Напомним, что объем
полусфера A = 2/3 p r 3
а объем цилиндра A = p
р 2 ч. Используйте 3.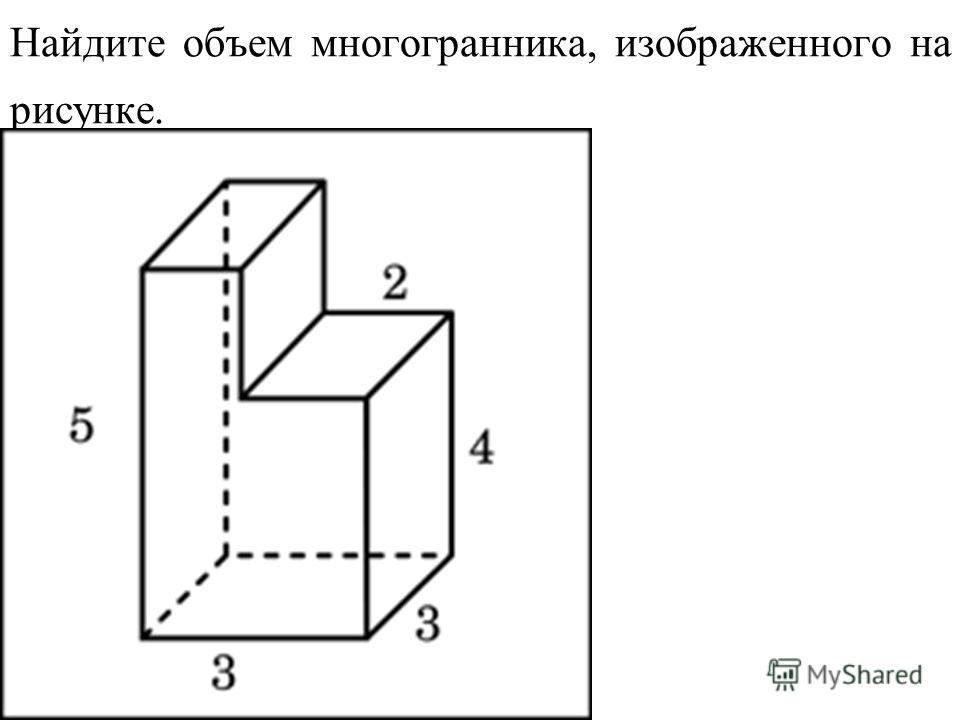
р и
0,67 для 2/3.
Округлите ответ до ближайшего целого числа.
Раствор
- Обратите внимание, что это твердое тело состоит из цилиндра и полусферы.
- Объем цилиндра
Объем цилиндра =
п р 2 ч≈ 3,14 (10) 2 (20)
= 3,14(100)(20)
= (314)(20)
= 6280
Объем полушария = 2/3
р 3
≈ (0,67)(3,14) (10 3 )
= (0,67)(3,14)(1000)
≈ 2104
- Теперь добавьте два тома, чтобы получить
при общем объеме.Общий объем = объем цилиндра + объем полушария
= 6280 + 2104
= 8384
Общий объем составляет 8384 кубических фута.
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку
на желтом прямоугольнике и появится ответ.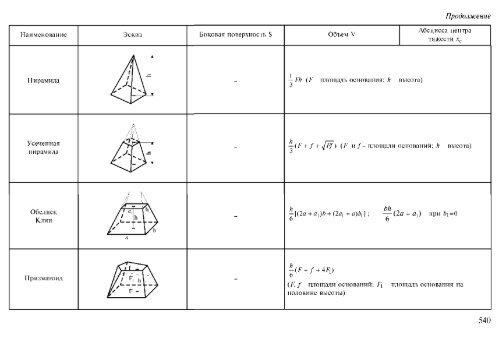
Упражнение 3
Башня образуется путем присоединения конуса высотой
30 футов на цилиндр радиусом
40 футов и высота 50
ноги, как показано ниже. Найдите объем башни. Объем
конус
Объем конуса =
1/3 п р 2 ч
и объем цилиндра
Объем цилиндра =
п р 2 ч
Использование
3.14 для р
и округлить ответ до ближайшего целого числа.
Ответить
Площадь поверхности
Существует множество различных типов проблем с площадью поверхности. Мы сосредоточимся
на нахождение площади поверхности, когда твердое тело состоит из кубов, каждый из которых имеет
одинаковая длина стороны. Чтобы решить такую задачу о площади поверхности, найдите площадь
сверху и снизу, слева и справа, спереди и сзади. Затем добавьте
области, чтобы получить общую площадь.
Пример 4
Однодюймовые кубы уложены, как показано на рисунке ниже.
общая площадь поверхности?
Раствор
Сначала найдем площади верха и низа. Заметь
эти области одинаковы. Глядя на верх сверху (или снизу
снизу), мы видим, что это просто прямоугольник.
Прямоугольник имеет основание 5 и высоту
4. Площадь
Площадь верха = (5)(4) = 20
Площадь дна тоже 20.
Теперь найдем площадь левой и правой сторон. Глядя с
правильно, мы также видим прямоугольник. Основание прямоугольника равно
4 и высота 2.
Его площадь
Площадь левой стороны = (4)(2) = 8
Площадь правой стороны тоже 8.
Далее находим площадь переда. Чтобы найти эту область, мы можем просто
считать квадраты. Есть 7 квадратов.
Площадь переда = 7
площадь спинки такая же, как и площадь переда. Это
площадь спины также равна 7. Мы могли бы
также получить площадь 7, разрезав фигуру
на два прямоугольника и суммируя площади этих прямоугольников.
Загрузить PDF
Загрузить PDF
Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.[1]
Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм3, см3, м3).[2]
Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.
-
1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.[3]
- Например, игральная кость – это куб.
-
2
Формула нахождения объема куба: V = s3, где V — объем, а s — длина ребра.
- Возведение в куб аналогично следующему умножению: s3 = s * s * s
-
3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
-
4
Подставьте длину ребра куба в формулу V = s3. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 53 = 5 * 5 * 5 = 125 см3 – это объем куба.
-
5
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 33 = 27см3.
Реклама
-
1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). [4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
-
2
Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.[5]
-
3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
-
4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
-
5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
-
6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см3.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Реклама
-
1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.[6]
- Например, банка или батарейка АА имеют форму цилиндра.
-
2
Формула нахождения объема цилиндра: V = πr2h, где V — объем, h — высота, r – радиус основания и πr2 — площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr2.
-
3
Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
-
4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
-
5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr2.
- Если радиус основания равен 4 см, то площадь основания равна π42.
- 42 = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см2
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
-
6
Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
-
7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr2h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4210
- π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см3.
Реклама
-
1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. [7]
Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
-
2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
-
3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s2, где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 62 = 36 см2
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.[9]
-
4
Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
-
5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
-
6
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см3.
Реклама
-
1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
-
2
Формула для вычисления объема конуса: V = 1/3πr2h, где r – радиус круглого основания, h – высота конуса.
- b = πr2 – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
-
3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr2.
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π32.
- π32 = π(3*3) = 9π.
- = 28,27 см2
-
4
Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
-
5
Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см2, а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
-
6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π325 = 47,12
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см3.
Реклама
-
1
Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). [11]
-
2
Формула для вычисления объема шара: V = 4/3πr3, где r – радиус шара.[12]
-
3
Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
-
4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
-
5
Возведите радиус в куб (r3). То есть r3 = r*r*r. В нашем примере r = 3, поэтому r3 = 3 * 3 * 3 = 27.
-
6
Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
-
7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см3.
Реклама
Об этой статье
Эту страницу просматривали 74 719 раз.
























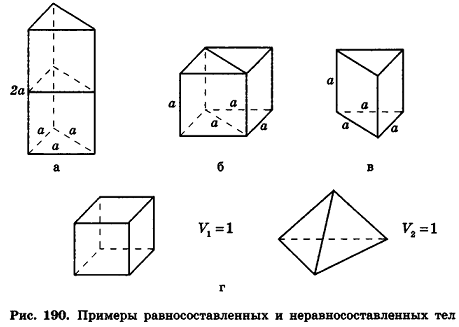
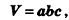
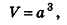
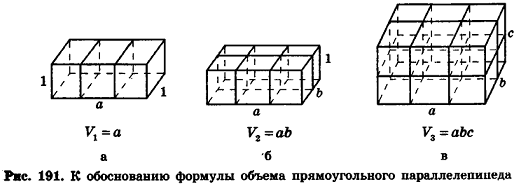
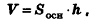
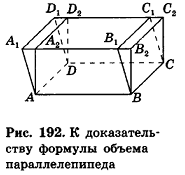
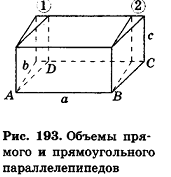
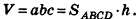
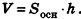
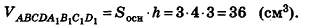
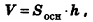
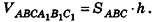
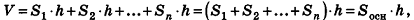
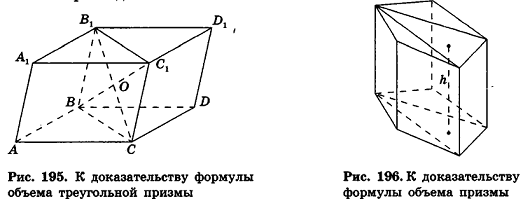
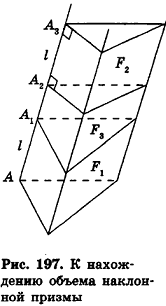
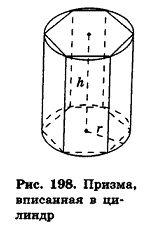
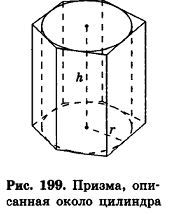
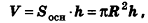
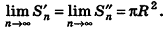
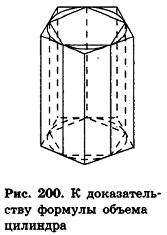
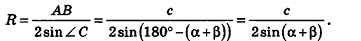
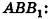
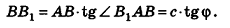
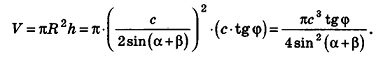
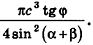
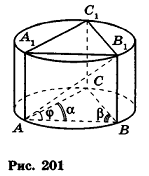
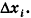
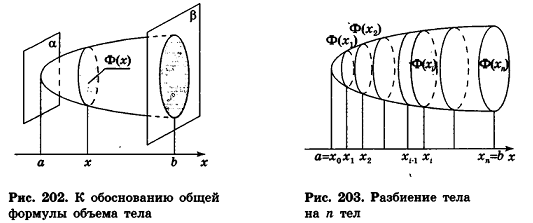
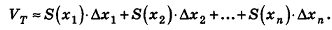
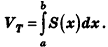
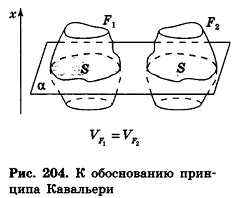
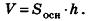
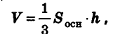
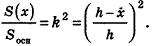
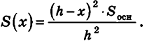
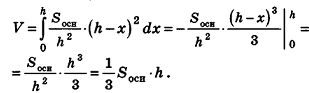
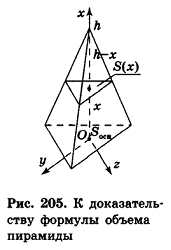
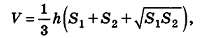
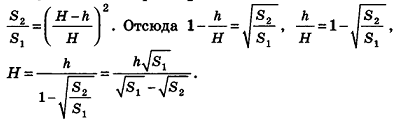
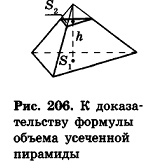
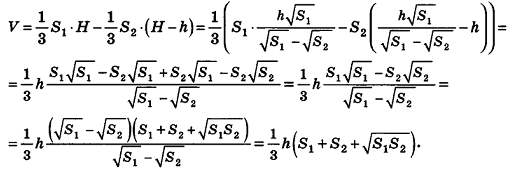
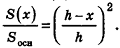
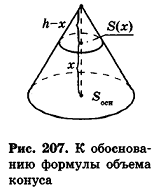
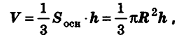
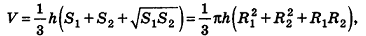
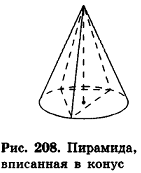
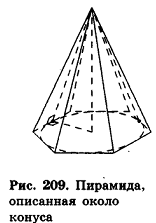
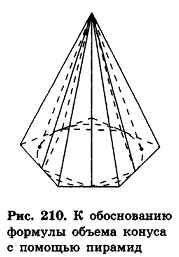
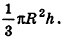
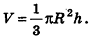
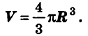
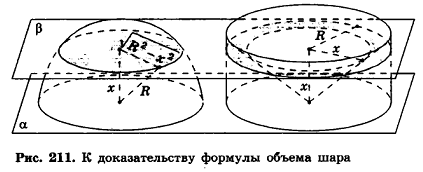
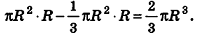
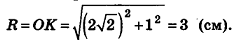
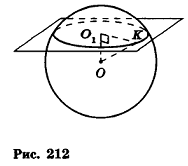
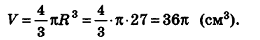
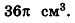
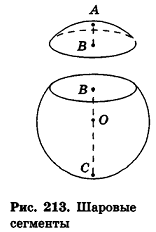
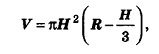
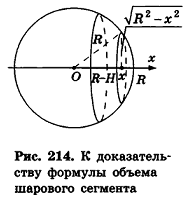
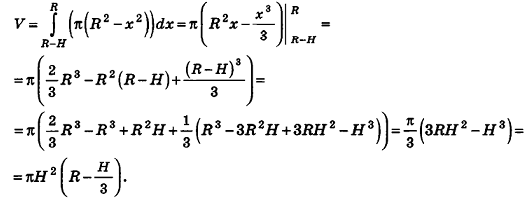
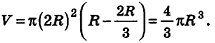
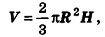
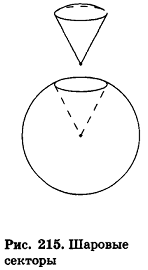
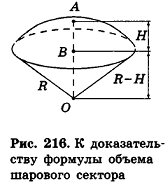
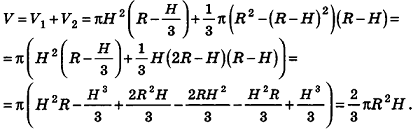
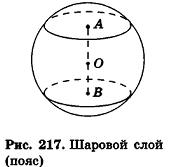
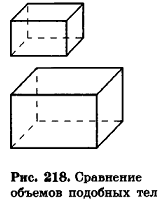
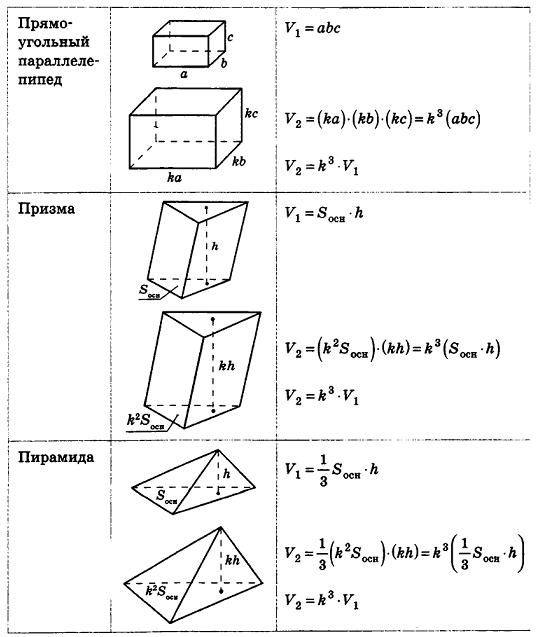
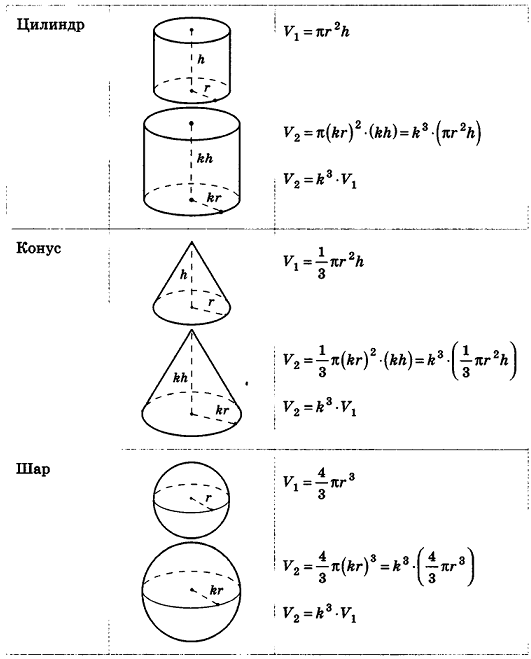
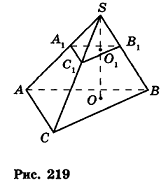
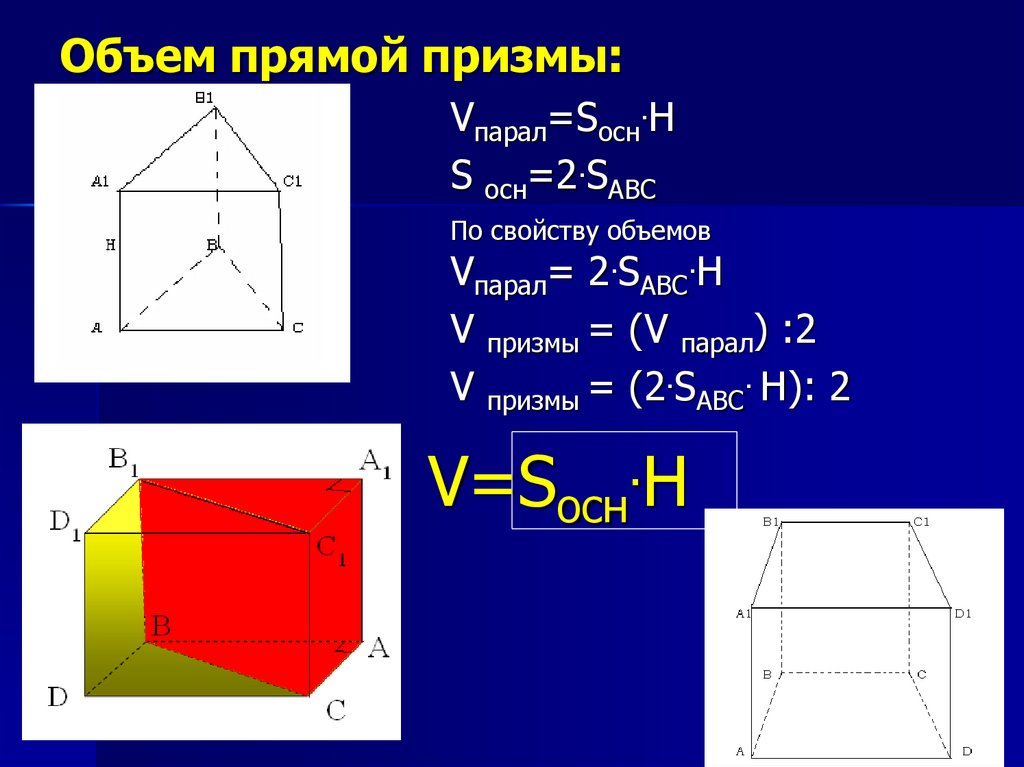
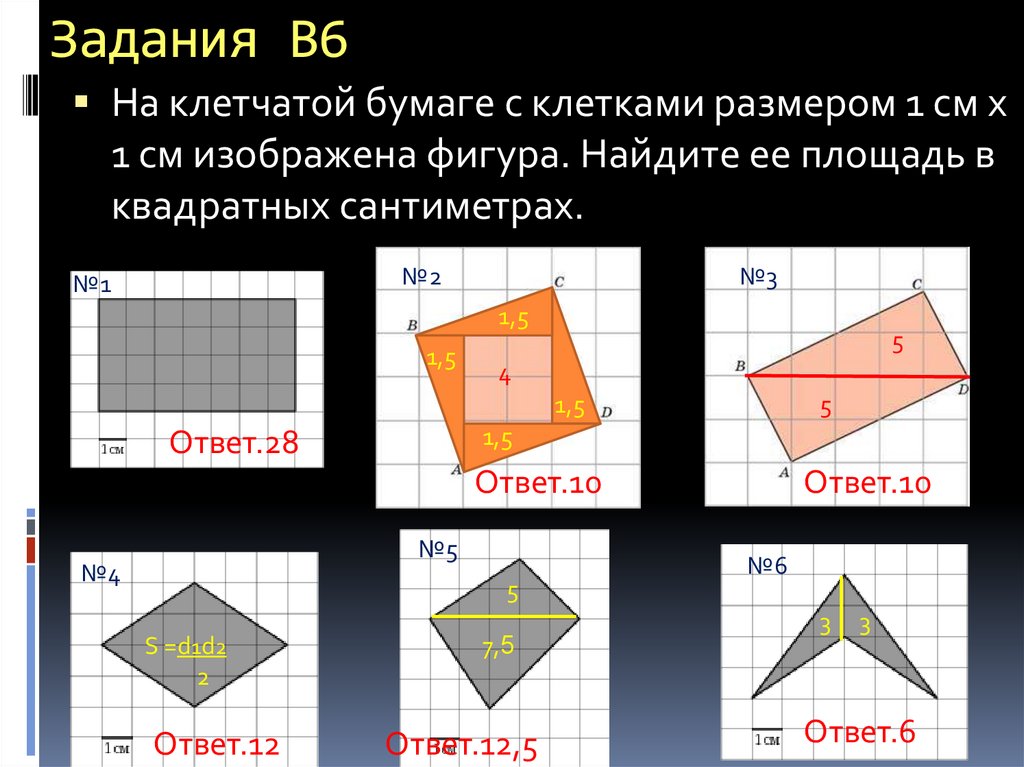
 Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
 Объем зернохранилища равен 87,178 м 3
Объем зернохранилища равен 87,178 м 3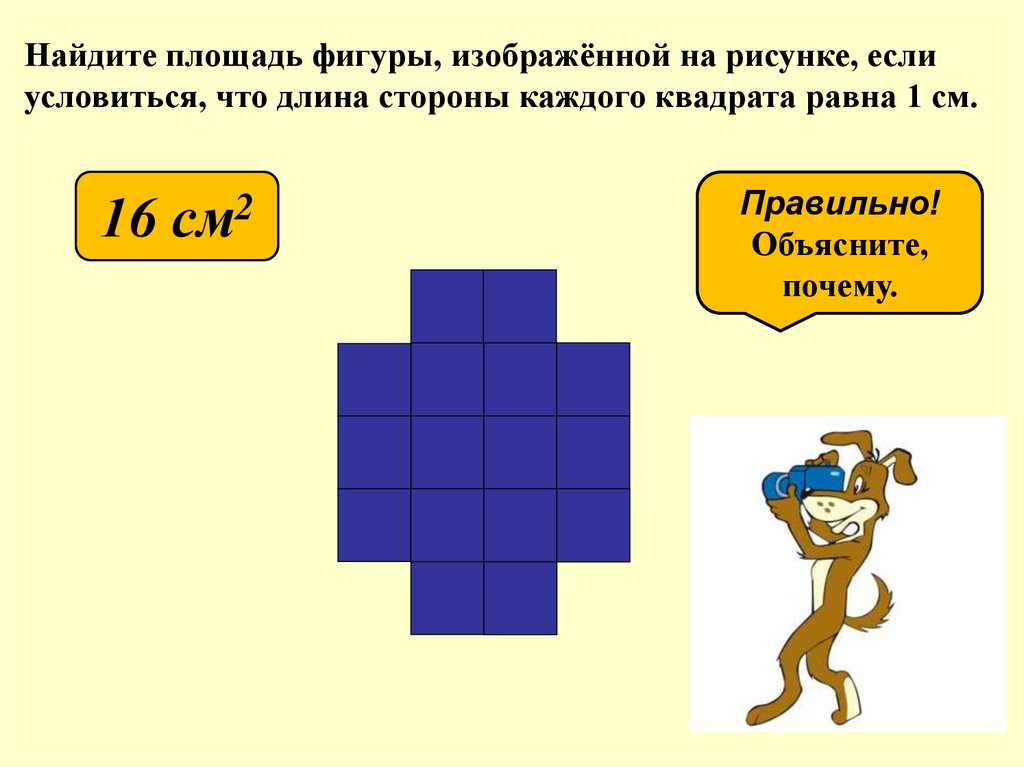
 Второй способ более точен, так как онлайн-калькулятор учитывает все данные: тип фундамента, сечение фундаментной базы, наличие арматурного каркаса и марку раствора.
Второй способ более точен, так как онлайн-калькулятор учитывает все данные: тип фундамента, сечение фундаментной базы, наличие арматурного каркаса и марку раствора.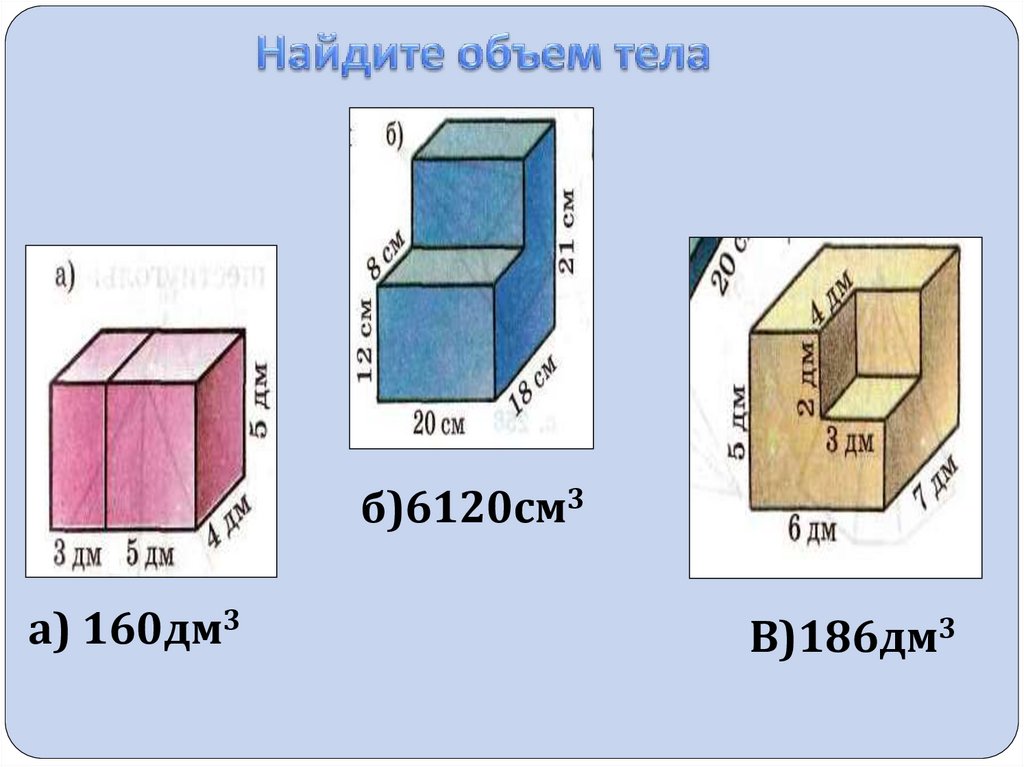
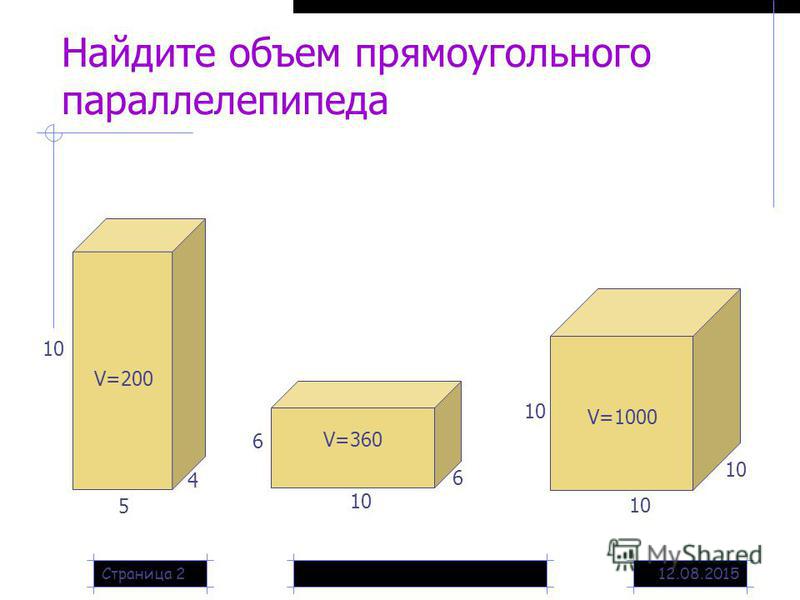

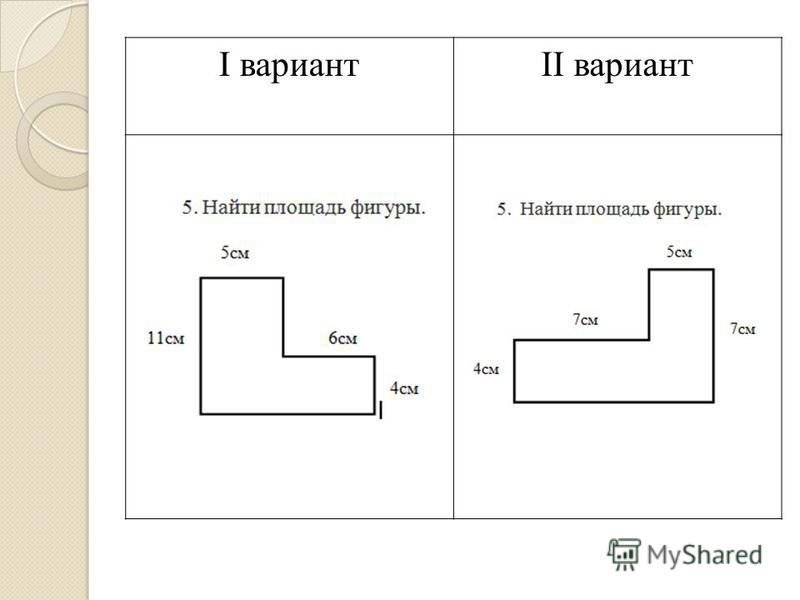 Возникают ситуации, когда черновая поверхность имеет уклон. В этом случае формируемая стяжка имеет разную толщину по площади помещения. В данной ситуации можно использовать усредненную толщину слоя, что снижает точность вычислений.
Возникают ситуации, когда черновая поверхность имеет уклон. В этом случае формируемая стяжка имеет разную толщину по площади помещения. В данной ситуации можно использовать усредненную толщину слоя, что снижает точность вычислений.