Объём части конуса. Для вас очередная статья с конусами – тип заданий, которые ранее присутствовали в открытом банке задач и вполне могут быть в составе ЕГЭ по математике. *На момент написания статьи эти задания из открытого банка удалены, но их всегда могут вернуть вновь.
Суть вопроса заключается в нахождении объёма части конуса. На блоге уже есть статья с заданиями, условия которых связаны с объёмом конуса, можете посмотреть.
Если сказать простым языком – рассматриваемое тело построено («стоит») на секторе круга, то есть нам необходимо найти объём некоторого «сектора конуса». Посмотрите для наглядности, это рисунки из задач:
Как вы догадались – процесс решения прост!
Главное определить центральный угол сектора круга, на котором построена («стоит») часть конуса.
Формула объёма конуса:
Пока рассмотрим общий подход к решению. Посмотрите на эскизы, мысленно представьте, что это вид конуса сверху:
Мы знаем, что полный круг составляет у нас 3600.
Если «отрежем» часть конуса соответствующую центральному углу в 1800 (то есть, пополам по оси), то объём части конуса будет равен половине объёма полного конуса (рис.1):
Если мы «вырежем» часть конуса, соответствующую центральному углу в 900, то объём этой части будет равен одной четвёртой объёма полного конуса (рис.2):
При этом объём оставшейся части будет равен ¾ от объёма полного конуса:
Если мы «вырежем» часть конуса, соответствующую центральному углу в 600, то объём этой части будет равен одной шестой объёма полного конуса (рис.4):
То есть необходимо величину центрального угла, которая соответствует части конуса разделить на 3600, и далее полученную величину умножаем на полный объём конуса. Общая формула:
Рассмотрим задачи:
25793. Найдите объем V части конуса, изображённой на рисунке. В ответе укажите V/Пи.
Объём конуса равен:
Объем части конуса равен:
n – центральный угол, которому соответствует часть конуса
Таким образом, искомый объём равен:
Результат разделим на Пи и запишем ответ.
Ответ: 216
27203. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/Пи.
Угол соответствующий указанной части конуса равен 3600 – 900 = 2700.
Таким образом, искомый объём будет равен:
Результат разделим на Пи и запишем ответ.
Ответ: 243
27204. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/Пи.
Угол соответствующий указанной части конуса равен 600.
Таким образом, искомый объём будет равен:
Результат разделим на Пи и запишем ответ.
Ответ: 216
27205. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/Пи.
Угол соответствующий указанной части конуса равен 3600 – 600 = 3000.
Таким образом, искомый объём будет равен:
Результат разделим на Пи и запишем ответ.
Ответ: 607,5
27202. Найдите объем части конуса, изображенной на рисунке.
В ответе укажите V/Пи.
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

{V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2)}
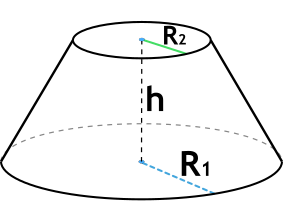
Радиус нижнего основания R1
Радиус верхнего основания R2
Усеченный конус — фигура, которую можно получить из конуса, если через него провести сечение, параллельное основанию.
Справедливо и другое определение.
Усеченный конус — тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.
Калькулятор объема конуса и формулы для расчета находится здесь.
Чтобы найти объем усеченного конуса необходимо знать три его характеристики — высоту (h), радиус нижнего основания (R1) и радиус верхнего основания (R2). Кроме того существует вторая формула объема усеченного конуса, для которой необходимо знать высоту конуса, а также площади его верхнего и нижнего оснований.
Содержание:
- калькулятор объема усеченного конуса
- формула объема усеченного конуса через радиусы оснований и высоту
- формула объема усеченного конуса через площади оснований и высоту
- примеры задач
Формула объема усеченного конуса через радиусы оснований и высоту
{V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2)}
h — высота усеченного конуса
R1 — радиус нижнего основания
R2 — радиус верхнего основания
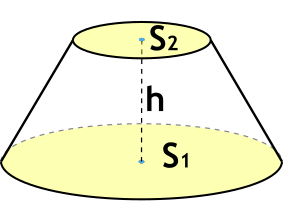
Формула объема усеченного конуса через площади оснований и высоту
{V=dfrac {h}{3} (S_1 + sqrt{S_1 cdot S_2} + S_2)}
h — высота усеченного конуса
S1 — площадь нижнего основания
S2 — площадь верхнего основания
Примеры задач на нахождение объема усеченного конуса
Задача 1
Найдите объем усеченного конуса радиусы оснований которого равны 1см и 2см, а высота равна 3см.
Решение
Для решения используем формулу объема усеченного конуса через высоту и радиусы оснований. Подставим известные нам значения в формулу и произведем расчет.
V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2) = dfrac {1}{3} pi cdot 3 cdot (2^2 + 2 cdot 1 + 1^2) = dfrac {1}{3} pi cdot 3 cdot (4 + 2 + 1) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = dfrac {21}{3} pi = 7 pi : см^3 approx 21.99115 : см^3
Ответ: 7 pi : см^3 approx 21.99115 : см^3
Полученный ответ легко проверить с помощью калькулятора .
Усечённый конус — тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.
| R2 — радиус меньшего основания;R1 — радиус большего основания;
(l) — образующая; (H) — высота |
Площадь боковой поверхности усечённого конуса
радиусы оснований, (l) — образующая.
Sполн.=Sбок.+S1+S2,гдеS1,S2
— площади оснований усечённого конуса.
Объём усечённого конуса
V=13π⋅H⋅(R12+R1⋅R2+R22)
, где (H) — высота усечённого конуса.
При решении задач чаще всего достаточно нарисовать только осевое сечение усечённого конуса, которое является равнобедренной трапецией.
Источники:
Рисунки © Якласс
Дополнения
1.О применении определённого интеграла для нахождения объёмов тел вращения
1.1.Формула объёма тела вращения
В п.16.2 дано определение тела вращения.
Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».
Пусть f(x) — непрерывная на отрезке [a; b] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).
Рис. 225
Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f(x), отрезками aA, bB и отрезком [a; b] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.
Рис. 226
Через произвольную точку х = с (a ⩽ с ⩽ b) отрезка [a; b] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f(с), а площадь — πf2(с) (или точка (c; 0)).
Объём части тела Ф, заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V(х). Заметим, что V(x) = V(a) = 0 при х = a; при х = b имеем V(x) = V(b) = V — искомый объём тела вращения Ф.
Покажем, что функция V(x) имеет производную V′(х) и V′(х) = πf2(х).
Придадим абсциссе х приращение ∆х > 0, тогда объём V(х) получает приращение ∆V(х) = V(x + ∆x) – V(x). Пусть m и М — соответственно наименьшее и наибольшее значения функции f(х) на промежутке [х; х + ∆х]. Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆V(x), а цилиндр, радиус основания которого равен M, содержит тело объёма ∆V(х); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆х. Объёмы этих цилиндров равны соответственно πm2•∆x и πM2•∆х. На основании свойства 2 объёмов (п. 10.1) получаем
πm2•∆x ⩽ ∆V(x) ⩽ πM2•∆x,
откуда
πm2 ⩽ 
Рассуждения для случая ∆х < 0 проводятся аналогично и дают тот же результат.
Пусть теперь ∆х 





или
πf2(х) ⩽ 
Значит, 

Таким образом, переменный объём V(x) телa вращения представляет собой одну из первообразных для функции πf 2(х) на отрезке [a; b]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль (V(a) = 0), а при х = b значение функции V(x) равно объёму тела вращения Ф (V(b) = V).
Если F(х) — также некоторая первообразная для функции πf 2(x), то V(x) = F(x) + С, где С — произвольная постоянная. Так как V (a) = 0, то из равенства V(a) = F (a) + C = 0 находим С = –F(a). Значит, V(x) = F(x) – F(a). Toгдa V(b) = F(b) – F(a). Ho V(b) = V — искомый объём тела вращения Ф. Таким образом, V = F(b) – F(a), где F(b) и F(a) — значения первообразной для функции πf 2(х) соответственно при х = b и х = a. Это означает, что
V = 

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f(x), х = a, х = b, у = 0, вычисляется по формуле
Рис. 227
V = 
ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = 
Решение. Воспользуемся формулой V = π

V = π


Ответ: 4π.
1.2. Объёмы конуса, шара и его частей
Используя формулу V = 
а) Объём конуса и усечённого конуса
Теорема 1 (об объёме полного конуса). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту:
V = 
Рис. 228
Доказательство. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О(0; 0), А(Н; 0) и B(Н; R) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у = 
V = 



где πR2 — площадь основания конуса. Теорема доказана. ▼
Теорема 2 (об объёме усечённого конуса). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н, радиусы оснований которых соответственно равны r, R и 
V = 
Доказательство. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O(0; 0), A(0; r), В(Н; R), С(H; 0) (рис. 229).

Прямая AВ проходит через точки (0; r) и (Н; R), поэтому её уравнение имеет вид у = 

V = 
Для вычисления интеграла сделаем замену переменных

Тогда 

что и требовалось доказать. ▼
б) Объём шарового слоя
В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х2 + у2 = R2, –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [a; b] оси Ох и отрезками aА и bВ прямых соответственно x = a и х = b (рис. 230, а).

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б). Найдём его объём, применяя формулу (*) п. 1.1.
Из уравнения х2 + у2 = R2 имеем у2 = R2 – x2. Поэтому для вычисления объёма V шарового слоя получаем:
Таким образом, объём шарового слоя, отсекаемого от шара x2 + y2 + z2 ⩽ R2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле
V = 
Пусть радиусы оснований шарового слоя равны r1 и r2 (r1 > r2), а высота — H (см. рис. 230, a).
Тогда Н = b – a, 

Формулу (**) преобразуем к виду:
V = 
= 
Из системы равенств (b – a)2 = H2, R2 – a2 = 

R2 – ab = 
Тогда:
V = 
= 
Таким образом, объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле
V = 
в) Объём шара
Рис. 231
При вращении полукруга х2 + у2 = R2 (расположенного в плоскости Оху, рис. 231, а) вокруг оси Ох образуется шар радиуса R (рис. 231, б). Из уравнения окружности х2 + y2 = R2 данного полукруга имеем у2 = R2 – х2. Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R:
Vш = 
= 
Таким образом, имеет место следующая теорема.
Теорема 3 (об объёме шара). Объём шара радиуса R вычисляется по формуле
Vш = 
г) Объём шарового сегмента
Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б).
Рис. 232
Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x2 + y2 = R2 (в плоскости Оxу), то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H, b = R, т. е.
Vш. сегм = 
=
Таким образом, имеет место следующая теорема.
Теорема 4 (об объёме шарового сегмента). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н, вычисляется по формуле
Vш. сегм =
Если в формуле (***) п. 1.2, б положить r2 = 0, r1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н:
Vш. сегм = 
д) Объём шарового сектора
Рис. 233
Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC = H — его высота; N — точка сферы (рис. 233).
Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.
Объём Vк конуса равен


Выразим r2 через R и H.
B прямоугольном треугольнике AOC находим r2 = AC2 = ОА2 – OC2 = R2 – (R – H)2 = H(2R – H).
Значит,
Vк = 

Для объёма шарового сегмента имеем:
Vш. сегм = 

= 
Тогда для объёма шарового сектора получаем
Vш. сект = Vк + Vш. сегм =
= 


Таким образом, доказана следующая теорема.
Теорема 5 (об объёме шарового сектора). Объём шарового сектора шара радиуса R вычисляется по формуле
Vш. сект = 
где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.
В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий. Решите самостоятельно следующие задачи.
1)Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = 
2)Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. (Ответ: 0,5π2.)
3)Найдите объём тела, полученного при вращении кривой у = 0,25х2 вокруг оси Оу в пределах от у = 1 до у = 5. (Ответ: 48π.)
4)Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2х2 и у = x3.
Сегодня на уроке мы вспомним, какие фигуры мы
назвали конусом, усечённым конусом, выведем формулы для вычисления объёма
конуса и усечённого конуса.
Конус – это один из видов тел вращения. Рассмотрим
произвольную плоскость , окружность
с
центром , лежащую в плоскости
и
прямую , перпендикулярную к
плоскости этой окружности. Через
точку и каждую точку
окружности проведём прямую.
Определение:
Поверхность, образованная этими прямыми, называется конической
поверхностью, а сами прямые – образующими конической
поверхности.
Точка называется вершиной,
а прямая называется осью
конической поверхности.
Мы давали такое определение. Тело, ограниченное
конической поверхностью и кругом с границей ,
называется конусом.
Вспомним элементы конуса.
Основанием
конуса называется круг, границей которого служит окружность .
Вершиной
конуса называется вершина конической поверхности.
Образующими
конуса называются отрезки образующих конической поверхности, заключённые между
его вершиной и основанием. Отметим, что все образующие конуса равны друг другу.
Боковой поверхностью
конуса называется фигура, образованная всеми образующими конуса.
Ось конической поверхности называется осью
конуса. А её отрезок (или его длина), заключённый между вершиной и основанием,
— высотой конуса.
Конус может быть получен вращением прямоугольного
треугольника вокруг одного из его катетов на .
На экране изображён конус, полученный вращением
прямоугольного треугольника вокруг катета
.
В этом случае основание конуса образуется вращением катета ,
а боковая поверхность конуса – вращением гипотенузы .
Теперь давайте сформулируем и докажем теорему.
Объём конуса равен одной трети произведения площади
основания на высоту.
Доказательство.
Рассмотрим конус с объёмом , радиусом основания
, высотой
и
вершиной в точке .
Проведём ось так, чтобы она
проходила черев высоту конуса. Любое сечение конуса плоскостью перпендикулярной
к оси является кругом с
центром в точке пересечения этой плоскости с осью .
Например, с центром в точке . Обозначим радиус
этого круга за , а площадь сечения
обозначим за , где икс – абсцисса
точки .
Поскольку ось проходит через высоту
конуса, то, значит, что ось перпендикулярна
плоскости основания, тогда плоскость сечения параллельна плоскости основания,
значит, можно записать, что . Из параллельности
этих отрезков следует равенство углов ,
, отсюда следует
подобие треугольников .
Из подобия можно записать равенство отношений . Отрезок
,
–
высота конуса, значит , тогда можно записать,
что отношение .
Отсюда нетрудно выразить . Площадь сечения равна
. Подставим вместо
его выражение через
радиус основания конуса, получим, что .
Для вычисления объёма воспользуемся основной
формулой для вычисления объёмов тел.
Пределы интегрирования от до
, получим, что объём
равен .
Что и требовалось доказать.
Следствием этой теоремы будет формула для вычисления
объёма усеченного конуса. Но прежде чем сформулировать следствие, давайте
вспомним, какую фигуру мы назвали усечённым конусом.
Усечённым конусом
называется часть конуса, расположенная между его основанием и секущей
плоскостью, перпендикулярной оси конуса.
Назовём элементы усечённого конуса.
Основание исходного конуса и круг, полученный в
сечении этого конуса плоскостью, называются основаниями усечённого
конуса.
Высотой усечённого
конуса называется отрезок (или его длина), соединяющий центры его оснований.
Прямая называется его осью.
Часть конической поверхности, ограничивающая усечённый
конус, называется его боковой поверхностью, а отрезки образующих
конической поверхности, расположенные между основаниями, называются образующими
усечённого конуса.
Все образующие усечённого конуса равны друг другу.
Усечённый конус может быть получен вращением на прямоугольной
трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Теперь сформулируем следствие.
Объём усечённого конуса, высота которой равна ,
а площадь оснований равны и
, вычисляется по
формуле:
Решим несколько задач.
Задача:
заполнить таблицу недостающими данными.
Решение:
в первой строке нам известны радиус основания конуса и высота конуса, для того,
чтобы найти объём конуса, воспользуемся только что доказанной формулой .
Занесём получившееся значение в ячейку.
Во второй строке нам даны объем конуса и радиус его
основания, для того чтобы найти высоту конуса, выразим из формулы объёма высоту
и получим . Занесём получившееся
значение в ячейку.
В третьей строке нам даны: объём конуса и его высота
нам необходимо найти радиус основания конуса. Подставим эти значения в
известную нам формулу, выразим из неё высоту конуса и получим .
Задача:
высота конуса равна . На расстоянии
от
вершины его пересекает плоскость, параллельная основанию. Найти объём исходного
конуса, если объём меньшего конуса, отсекаемого от исходного, равен .
Решение:
так как плоскость пересекает конус на расстоянии от
вершины, значит, высота меньшего конуса равна 2 см.
Тогда зная объём меньшего конуса нетрудно найти
радиус основания меньшего конуса .
Большой конус и маленький конус подобны, поэтому
можно записать равенства отношений .
Отсюда нетрудно найти, что радиус основания большого
конуса равен .
Тогда, подставив найденные значения в формулу для
вычисления объёма, получим, что объём конуса равен .
Задача:
радиусы оснований усечённого конуса равны и
, а образующая конуса
равна . Найти объём усечённого
конуса.
Решение:
построим осевое сечение усечённого конуса.
В осевом сечении будет равнобедренная трапеция,
основаниями которой будут диаметры оснований конуса, а боковыми сторонами будут
образующие усечённого конуса.
Опустим высоты трапеции, эти высоты будут равны
высоте конуса. Поскольку трапеция равнобедренная, значит, высоты разбивают
трапецию на два равных прямоугольных треугольника и прямоугольник.
Нетрудно найти, что высота трапеции, а значит и
усеченного конуса будет равна:
Вычислим площади оснований усечённого конуса.
Подставим найденные значения в формулу для
вычисления объёма усеченного конуса и получим, что объём усечённого конуса
равен .
Итоги:
Сегодня на уроке мы вспомнили, какие фигуры
называются конусом и усечённым конусом, вывели формулы для вычисления объёмов
конуса и усечённого конуса. Решили насколько задач.