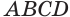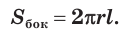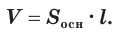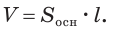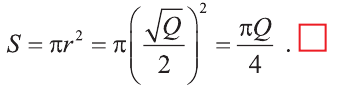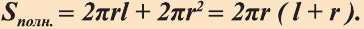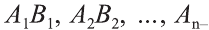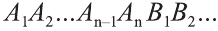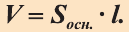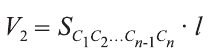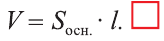Для определения объема цилиндра надо знать величины Н и D .
Из чертежа видно Н = СВ,а D =2*Н (углы в треугольнике АСВ 60° и 30°).
Известно из данных S=64 осевого сечения.Понятно что стороны сечения раны высоте и диаметру цилиндра и соотношение их 1:2.
Определим величену (1). ОО¹СВ = 64:2=32 =ОВ*СВ;и ОВ = СВ =32^ =5,6568.
СВ =5,65685
D =11,313708
Проверим.11,313708*5,65685=63,9999.
Определим объем: D²*3,14/4 *Н.
11,313708*11,313708=128,0000
128:4=32
32*3,14=100,48.
Далее умножим на Н
100,48*5,65685 = 568,4003
Найденый объем цилиндра 568,4003
Примечание. Это урок с решениями задач по геометрии (раздел цилиндр). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача
Осевое сечение цилиндра — квадрат, диагональ которого равна 4√2.
Вычислить объем цилиндра.
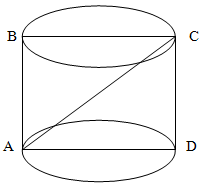
Решение.
Поскольку диагональ сечения цилиндра — квадрат, то обозначим его сторону как a.
a2 + a2 = (4√2)2
2a2 = 32
a2 = 16
a = 4
Объем цилиндра найдем по формуле:
V = πd2 / 4 * h
откуда
V = π42 / 4 * 4
V = 16π
Ответ: Объем цилиндра равен 16π
Задача
Куб с ребром длиной а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.
Решение.
Проведем плоскость через основание цилиндра.

Диагональ куба является одновременно диаметром цилиндра. Зная сторону куба, определяем длину диагонали AC квадрата ABCD как
CD2 + AD2= AC2
a2 + a2 = AC2
2a2 = AC
AC = a√2
Проведем плоскость через ось цилиндра по диагонали AC. Высота сечения равна длине ребра куба и по условиям задачи рана а, а ширина сечения равна a√2.
Таким образом, площадь сечения равна:
S = a * a√2 = a2√2
Ответ: a2√2
Задача
Диагональ осевого сечения цилиндра равна 12 см и образует с плоскостью нижнего основания угол 45 градусов. Найти обьём цилиндра.
Решение.
Поскольку основание осевого сечения образует с высотой цилиндра, принадлежащей сечению, прямой угол, то треугольник, который образован диагональю осевого сечения, высотой цилиндра и его диаметром — прямоугольный.
Исходя из этого, угол между диагональю и высотой также равен 45 градусов ( 180 — 90 — 45 ).
Таким образом, треугольник является равнобедренным, а, следовательно, высота цилиндра равна его диаметру. Применив теорему Пифагора, найдем их.
d2 + d2 = 122
2d2 = 144
d2 = 72
Теперь применим формулу объема цилиндра V = пd2 / 4 h
V = 72п / 4 * √72
V = 18п * √72
Ответ: 18п√72
Задача
|
Высота цилиндра 2м. Радиус основания 7м. В этот цилиндр наклонно вписан квадрат так, что все вершины его лежат на окружностях оснований. Найти сторону квадрата. |
Висота циліндра 2м. Радіус основи 7м. В цей циліндр похило вписаний квадрат так, що всі вершини його лежать на окружностях основ. Знайти сторону квадрата. |
Решение. Рiшення.
|
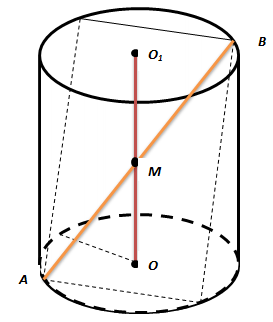
В силу симметричности квадрата и цилиндра и ввиду того, что квадрат наклонный, диагональ квадрата пересечет ось цилиндра ОО1 в точке М, являющейся серединой отрезкаОО1. По условию ОО1=2м, а ОА=7 м, поэтому ОМ=1м.
Пусть d – диагональ квадрата. Тогда сторона квадрата а равна: |
У силу симетричності квадрата і циліндра і зважаючи на те, що квадрат похилий, діагональ квадрата перетне вісь циліндра ОО1 в точці М, яка є серединою відрізка ОО1. За умовою ОО1=2м, а ОА=7 м, тому ОМ=1м.
Позначимо d – діагональ квадрата. Тоді сторона квадрата а: |
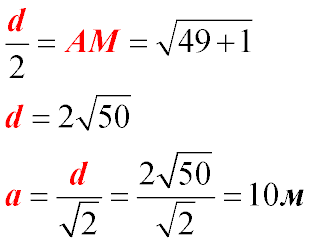
0
Цилиндр и его сечения |
Описание курса
| Диагональ цилиндра
Содержание:
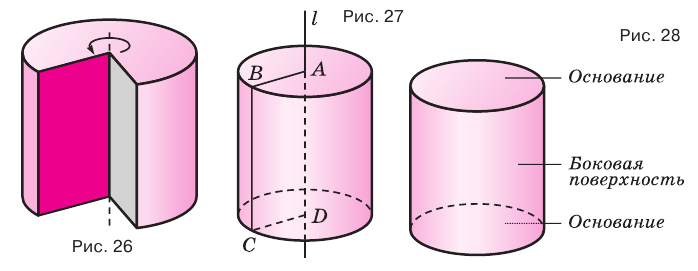
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника
Образующая цилиндра является его высотой.
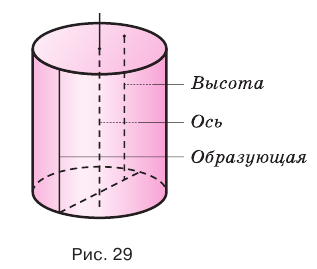
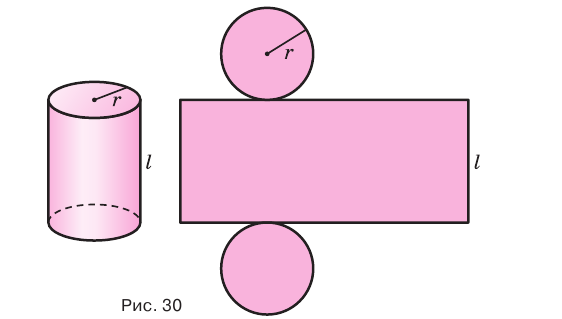
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Теорема 4.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
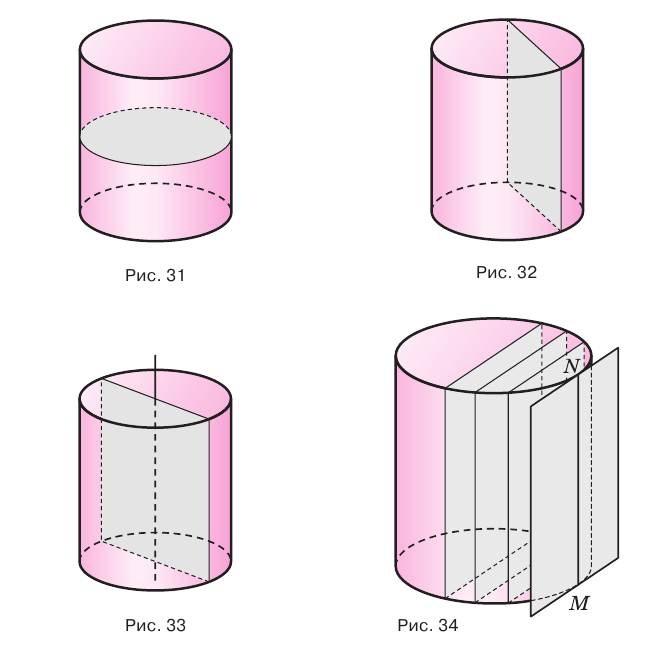
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую 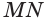
Теорема 5.
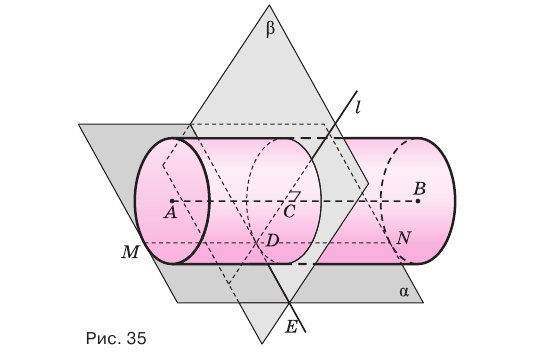
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 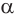
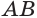
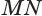
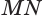
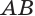
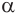
Проведем прямую 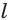
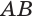
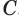
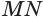
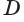
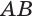
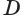
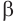
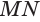
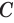
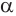
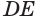
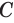
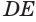
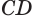
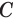
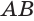
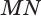
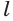
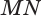
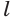
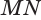
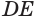
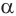
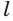
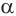
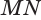
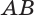
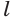
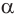
Теорема 5 выражает свойство касательной плоскости цилиндра.
Теорема 6.
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 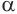
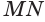
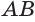
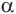
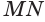
Пусть 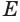
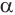
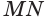
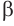
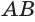
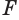
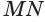
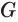
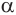
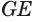
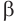
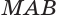
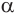
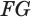
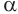
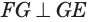
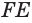
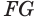
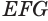
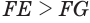
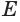
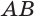
Теорема 6 выражает признак касательной плоскости цилиндра.
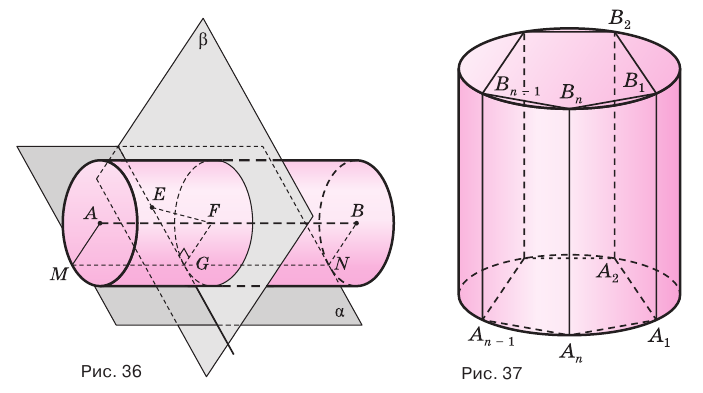
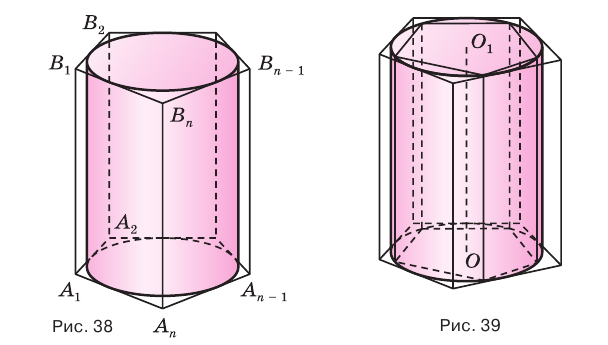
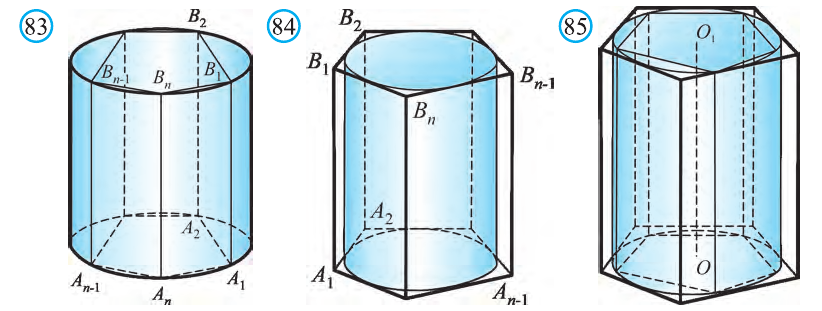
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 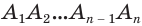
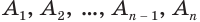
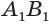
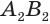
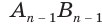
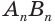
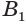
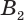
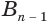
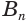
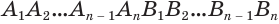
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Теорема 7.
Объем цилиндра равен произведению площади его основания и образующей:
Доказательство:
Пусть имеется цилиндр с осью 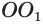
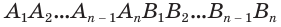
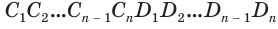
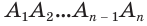
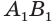
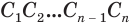
Будем количество 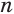
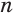
В описанном процессе высота 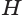
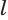
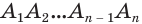
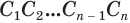
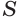
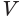
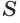
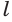
Поверхность цилиндра
Ещё один важный класс пространственных фигур — тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
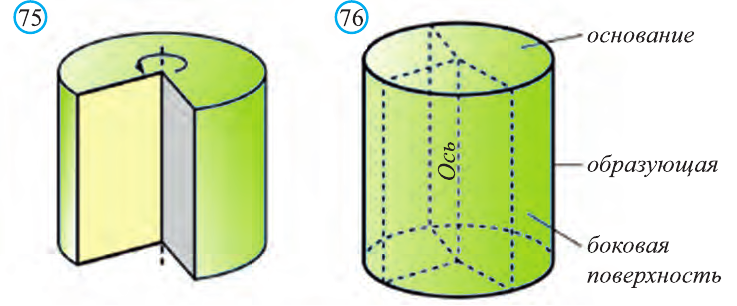
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76).
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
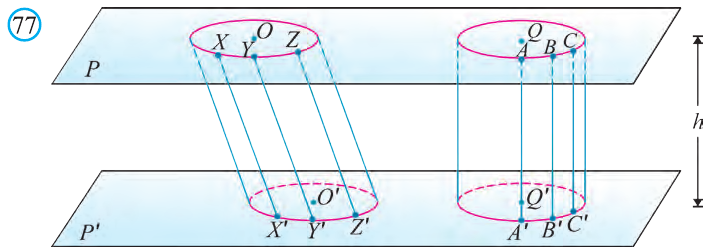
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
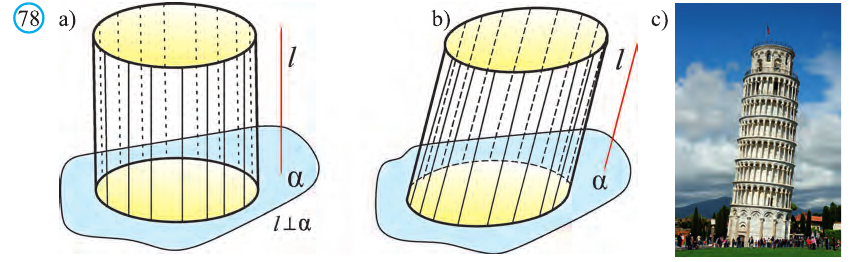
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра.
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
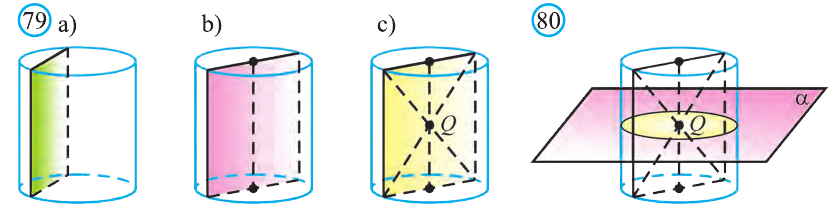
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны — это образующие цилиндра, а две другие стороны — соответствующие параллельные хорды оснований цилиндра.
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
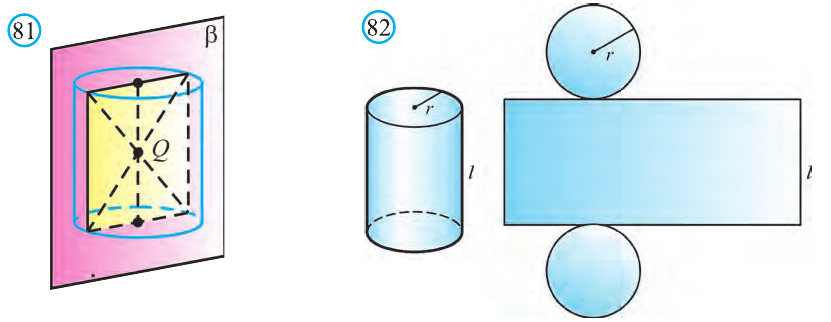
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Пример:
Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Решение:
Сторона квадрата равна 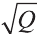
основания. Поэтому его площадь равна
Докажите самостоятельно эту теорему пользуясь рисунком 82.
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
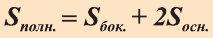
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 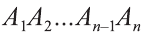
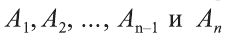
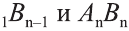
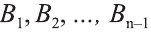
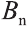
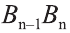
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра:
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 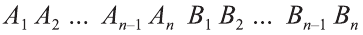
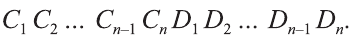
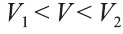
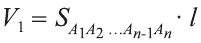
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 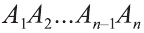
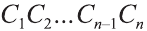
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб — физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма — представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма — тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.
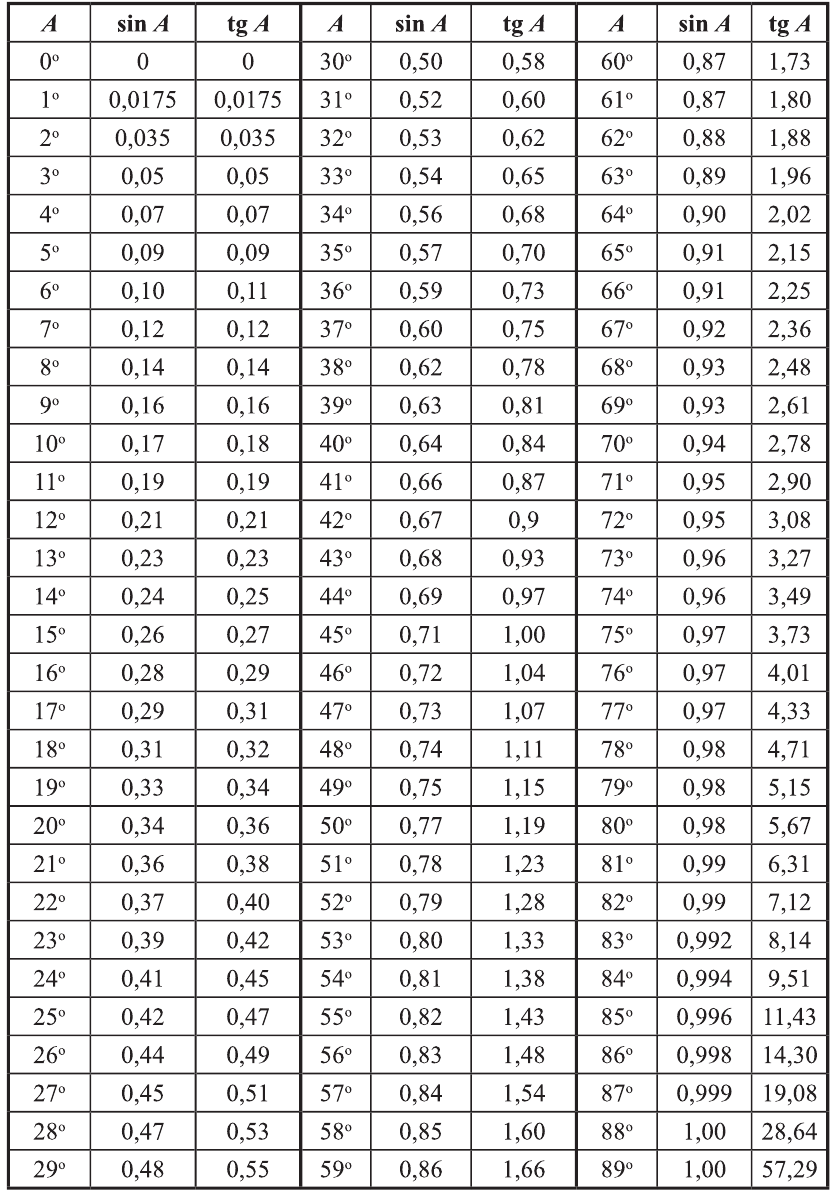
Таблица приближенных значений тригонометрических функций:
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
Как посчитать объем цилиндра
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать объем цилиндра
Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра если его радиус
r = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r2⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра если его диаметр
d = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(d/2)2⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Зная площадь основания So и высоту h
Чему равен объем цилиндра если площадь его основания
So = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
V = So⋅h
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:
V = 10 ⋅ 5 = 50 см3
Зная площадь боковой поверхности Sb и высоту h
Чему равен объем цилиндра если площадь его боковой поверхности
Sb = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
V = Sb2/4πh
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:
V = 302/ 4 ⋅ 3.14⋅ 5 = 900/62.8 = 14.33 см3
См. также
Главная
Как найти объём цилиндра зная площадь осевого сечения цилиндра и его высоту?
-
- 0
-
?
Станислав Лавенков
Вопрос задан 29 сентября 2019 в
5 — 9 классы,
Геометрия.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
Объем цилиндра равен произведению площади основания на высоту.
Диаметр основания = S сеч : h r= (S сеч : h)/2
Площадь основания = πr²=π(S сеч : h)/2)²
Объём цилиндра = h*π(S сеч : h)/2)²
Отмена
Тимофей Уразгильдеев
Отвечено 29 сентября 2019
-
Комментариев (0)
Добавить
Отмена