Как найти объем цилиндра егэ - Исправление недочетов и поиск решений вместе с Examum.ru

Каталог заданий.
Цилиндр

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В цилиндрический сосуд налили 2000 см³ воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.

Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания  — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи .

В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.

Пройти тестирование по этим заданиям

Источник

10
Сен 2013

Категория: 02 Стереометрия

02. Цилиндр.

2013-09-10
2022-09-11

Задача 1. Радиус основания цилиндра равен высота равна Найдите площадь боковой поверхности цилиндра, деленную на .

Решение: + показать

Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен Найдите высоту цилиндра.

Решение: + показать

Задача 3. Длина окружности основания цилиндра равна высота равна Найдите площадь боковой поверхности цилиндра.

Решение: + показать

Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на .

Решение: + показать

Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м).

Решение: + показать

Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Решение: + показать

Задача 7. В цилиндрический сосуд налили см воды. Уровень воды при этом достигает высоты см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на см. Чему равен объем детали? Ответ выразите в см

Решение: + показать

Задача 8. В цилиндрический сосуд налили см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в раза. Найдите объем детали.

Ответ выразите в см

Решение: + показать

Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в сантиметрах.

Решение: + показать

Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Вы можете пройти тест “Цилиндр”

Автор: egeMax |

комментария 3

Печать страницы

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на тему «Цилиндр»

Прямой цилиндр:

(blacktriangleright) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.

(blacktriangleright) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.

(blacktriangleright) Площадь боковой поверхности цилиндра ({Large{S_{text{бок.пов.}}=2pi rh}}), где (r) – радиус основания, (h) – высота (или образующая).

(blacktriangleright) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. [{Large{S_{text{полн.пов.}}=2pi rh+2pi r^2}}]

(blacktriangleright) Объем цилиндра ({Large{V=S_{text{осн}}cdot
h=pi r^2h}})

Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.

Задание
1

#2743

Уровень задания: Равен ЕГЭ

Про прямые круговые цилиндры (C_1) и (C_2) известно, что у (C_1) радиус основания в два раза больше, чем у (C_2), но у (C_2) высота в три раза больше, чем у (C_1). Найдите отношение объёма цилиндра (C_2) к объёму (C_1).

Обозначим высоту цилиндра (C_1) через (h_1), а высоту цилиндра (C_2) через (h_2). Обозначим радиус основания цилиндра (C_1) через (r_1), а радиус основания цилиндра (C_2) через (r_2). Тогда [r_1 = 2r_2,qquad h_2 = 3h_1,.]

Объём цилиндра (C_1) равен (pi {r_1}^2 h_1 = 4pi {r_2}^2 h_1), а объём цилиндра (C_2) равен (3pi {r_2}^2 h_1), тогда [dfrac{V_{C_2}}{V_{C_1}} = dfrac{3pi {r_2}^2 h_1}{4pi {r_2}^2 h_1} = 0,75]

Ответ: 0,75

Задание
2

#1861

Уровень задания: Равен ЕГЭ

Объем цилиндра равен (64pi), а площадь боковой поверхности равна (32pi). Найдите площадь полной поверхности цилиндра, деленную на (pi).

Формулы для нахождения объема и боковой поверхности цилиндра: (V = pi R^2 h), (S_{text{бок}} = 2pi R h). Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: [frac{V}{S_{text{бок}}} = frac{pi R^2 h}{2pi R h} = frac{R}{2} = frac{64pi}{32pi} = 2] (Rightarrow) (R = 4). Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: [S_{text{полн}} = 2pi R h + 2 pi R^2 = 32pi + 2 cdot 16pi = 64pi.] Осталось разделить полученный объем на (pi), тогда окончательно получаем (64).

Ответ: 64

Задание
3

#1862

Уровень задания: Равен ЕГЭ

Объем цилиндра равен (100pi), а площадь боковой поверхности равна (25pi). Найдите высоту цилиндра.

Формулы для нахождения объема и боковой поверхности цилиндра: (V = pi R^2 h), (S_{text{бок}} = 2pi R h). Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: [frac{V}{S_{text{бок}}} = frac{pi R^2 h}{2pi R h} = frac{R}{2} = frac{100pi}{25pi} = 4] (Rightarrow) (R = . Подставим значение радиуса в формулу объема и найдем из этой формулы искомую высоту: [V = pi R^2 h = 64pi h = 100pi] (Rightarrow) (displaystyle h = frac{100}{64} = 1,5625).

Ответ: 1,5625

Задание
4

#953

Уровень задания: Равен ЕГЭ

Объём цилиндра [V = dfrac{200}{sqrt{pi}},] а отношение радиуса его основания к его высоте равно (5). Найдите площадь полной поверхности этого цилиндра.

[V_{text{цил}} = pi R^2 H = dfrac{200}{sqrt{pi}},] (dfrac{R}{H} = 5), где (R) – радиус основания цилиндра, (H) – его высота, тогда (R = 5H), следовательно, [pi cdot 25 H^3 = dfrac{200}{sqrt{pi}}qquadRightarrowqquad H^3 = dfrac{8}{pisqrt{pi}},] откуда (H = dfrac{2}{sqrt{pi}}), (R = dfrac{10}{sqrt{pi}}). [S_{text{полн}} = 2pi R H + pi R^2 = 2pi R(H + R) = 2picdotdfrac{10}{sqrt{pi}}cdotdfrac{12}{sqrt{pi}} = 240.]

Ответ: 240

Задание
5

#952

Уровень задания: Сложнее ЕГЭ

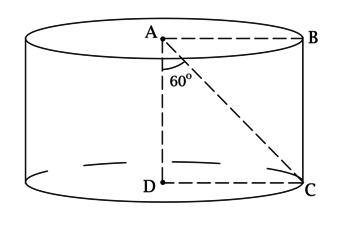
(AD) – ось цилиндра, (BC) – его образующая, (S_{ABCD} = dfrac{16sqrt{3}}{sqrt[3]{pi^2}}), (angle CAD = 60^circ). Найдите объём цилиндра.

Так как (AD) и (BC) – высоты цилиндра, то (ABCD) – прямоугольник, тогда [S_{ABCD} = ADcdot DC = Hcdot R = dfrac{16sqrt{3}}{sqrt[3]{pi^2}}.]

Рассмотрим прямоугольный треугольник (ADC):
Т.к. (angle DAC = 60^circ), то [AD = mathrm{tg}, angle ACDcdot DC = mathrm{tg}, 30^circcdot R = dfrac{R}{sqrt{3}},] т.е. (H = dfrac{R}{sqrt{3}}) или (R = sqrt{3}H).

Подставляя выражение для (R) в (S_{ABCD}), получим: [H^2cdotsqrt{3} = dfrac{16sqrt{3}}{sqrt[3]{pi^2}},] откуда (H = dfrac{4}{sqrt[3]{pi}}), тогда (R = dfrac{4sqrt{3}}{sqrt[3]{pi}}).

[V_{text{цил}} = pi R^2 H = picdot dfrac{16cdot 3}{sqrt[3]{pi^2}}cdotdfrac{4}{sqrt[3]{pi}} = 192.]

Ответ: 192

Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.

Основные нюансы, которые стоит вспомнить

Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.

Важно помнить, что:

Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
Высота цилиндра есть расстояние между плоскостями его оснований.
Все его образующие являются параллельными и равными между собой.
Радиус цилиндра есть радиус его основания.
Фигура называется прямой, если ее образующие перпендикулярны основаниям.

Как подготовиться к экзамену качественно и эффективно?

Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.

Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.

Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.

Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».

Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.

УСТАЛ? Просто отдохни

Источник

Цилиндр

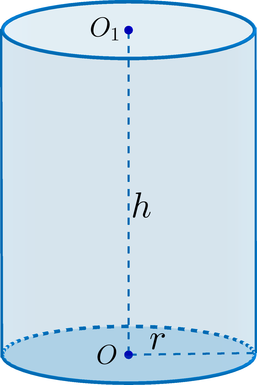
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая L.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.

Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в $m$ раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.

Пример:

Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.

Решение:

Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и высоты уровней жидкостей.

$V_1=V_2$;

$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого.

$h_1=40;h_2-?$

Распишем объемы занимаемой жидкости в обоих сосудах и приравняем формулы друг к другу.

$V_1=πR_1^2·h_1=πR_1^2·40$;

$V_2=πR_2^2·h_2=π(2R_1)^2·h_2=4πR_1^2·h_2$.

$πR_1^2·40=4πR_1^2·h_2$

Получили уравнение, которое можно разделить на $πR_1^2$

$40=4 h_2$

Чтобы найти $h_2$ надо сорок разделить на четыре

$h_2=10$

Ответ: $10$

Площадь поверхности и объем цилиндра

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

$S_{полн.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V= πR^2· h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Составной цилиндр:

Чтобы найти объем составного цилиндра надо:

Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
Найти объем каждого цилиндра.
Сложить объемы.

Источник

Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы

Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности

Стереометрия на ЕГЭ по математике присутствует и в 1 части, и во второй. Чтобы решать задачи, для начала надо выучить формулы. Все они есть в наших таблицах:

Куб, параллелепипед, призма, пирамида. Объем и площадь поверхности
Цилиндр, конус, шар. Объем и площадь поверхности

Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.

Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.

Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.

Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины», «грани» и «ребра». Вот они, на картинке.

Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.

Вам могут также встретиться понятия «прямая призма», правильная призма», «правильная пирамида».

Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.

Перейдем к практике.

1. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:

Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.

Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем:

А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей». В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется?

На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.

Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна 110 . А как повлияет на него вырезанная «полочка»?

Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна .

А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна ! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна 110 . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.

Ответ: 110 .

2. Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:

. Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной — на верхней и нижней гранях.

Ответ: 92.

3. А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.

Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Ответ: .

Следующий тип задач — когда одно объемное тело вписано в другое.

4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.

Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна , высота равна , объем равен .

Ответ: 4.

5. В основании прямой призмы лежит прямоугольный треугольник с катетами и . Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите .

Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна . Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: 100 .

Ответ: 100.

6. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.

Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.

Ответ: .

Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.

7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.

Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в раза уменьшится высота.
Ответ: .

8. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.

Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен pi R^2h .

	Высота	Радиус	Объем
Первая кружка
Вторая кружка	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}h$		$picdot left( 2R right)^2cdot genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}h$

Считаем объем второй кружки. Он равен $picdot left( 2R right)^2cdot genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}h=2 pi R^2h$ . Получается, что он в два раза больше, чем объем первой.

Следующая задача тоже решается сразу и без формул.

9. Через среднюю линию основания треугольной призмы, объем которой равен , проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

Высота меньшей призмы такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен .

И еще одна классическая задача. Никаких формул!

10. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?

Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в раз, поскольку 3^2=9 .
Ответ: .

Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды. Они тоже решаются элементарно.

11. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите .

Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом градусов, а $60^{circ}$ — это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на , записываем ответ: 937,5 .

Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник