Как найти объем цилиндра описанного около конуса - Исправление недочетов и поиск решений вместе с Examum.ru

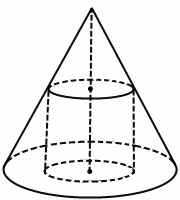
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.

Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.

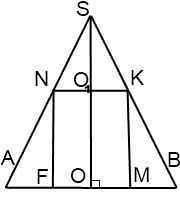
Рассмотрим осевое сечение комбинации тел. Оно представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

Здесь SO=H — высота конуса, OA=OB=R — радиус конуса, OF=OM=r — радиус цилиндра, OO1=h — высота цилиндра, SA=SB=l — образующие конуса, NF=KM=h — образующие цилиндра.

Прямоугольные треугольники SOB и KMB подобны (по общему острому углу B). Из подобия треугольников следует пропорциональность соответствующих сторон:

$[frac{{SO}}{{KM}} = frac{{OB}}{{MB}}, Rightarrow frac{H}{h} = frac{R}{{R - r}}.]$

Найдем отношение объемов конуса и вписанного в него цилиндра:

$[frac{{{V_1}}}{{{V_2}}} = frac{{frac{1}{3}pi {R^2}H}}{{pi {r^2}h}} = frac{1}{3} cdot frac{{{R^2}}}{{{r^2}}} cdot frac{H}{h}]$

С учетом предыдущего соотношения для высот конуса и цилиндра, имеем:

$[frac{{{V_1}}}{{{V_2}}} = frac{1}{3} cdot frac{{{R^2}}}{{{r^2}}} cdot frac{R}{{R - r}} = frac{{{R^3}}}{{3{r^2}(R - r)}}.]$

Найдем отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра:

$[frac{{{S_1}}}{{{S_2}}} = frac{{pi Rl}}{{2pi rh}} = frac{{Rl}}{{2rh}}]$

Из прямоугольного треугольника SOB по теореме Пифагора

$[S{B^2} = O{B^2} + S{O^2}, Rightarrow l = sqrt {{R^2} + {H^2}} ]$

Таким образом,

$[frac{{{S_1}}}{{{S_2}}} = frac{{Rsqrt {{R^2} + {H^2}} }}{{2rh}}.]$

Источник

Задания

Версия для печати и копирования в MS Word

Задания Д13 № 269425

Конус вписан в цилиндр. Объем конуса равен 53. Найдите объем цилиндра.

Решение.

Это задание ещё не решено, приводим решение прототипа.

Конус вписан в цилиндр. Объем конуса равен 5. Найдите объем цилиндра.

Поскольку

а конус и цилиндр имеют общую высоту и основание, имеем:

Ответ: 15.

Аналоги к заданию № 245350: 269433 269437 269365 … Все

Прототип задания

Источник

Геометрия, 11 класс

Урок №10. Комбинации тел вращения

Перечень вопросов, рассматриваемых в теме:

комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.

Глоссарий по теме

Определение

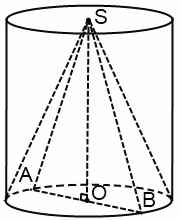
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.

Определение

Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Комбинации цилиндра и конуса

Определение

В любой конус можно вписать цилиндр.

Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

SO=H — высота конуса

OA=OB=R — радиус конуса

OF=OM=r — радиус цилиндра

OO₁=h — высота цилиндра

SA=SB=L — образующие конуса

NF=KM=h (l)— образующие цилиндра.

∆SOB и ∆KMB — прямоугольные

∆SOB∆KMB (по общему острому углу B)

Поэтому:

, то есть: .

Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)

, то есть .

Таким образом:

Определение

В любой цилиндр можно вписать конус.

OS — ось цилиндра и ось конуса, высота цилиндра и конуса

OA — радиус конуса и радиус цилиндра

SA=SB=L — образующие конуса,

CA=DB=l — образующие цилиндра

∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные

∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S_∆ASB=2S_ACDB.

Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)

, то есть .

2. Комбинация двух конусов

Определение

OS — ось конусов, высота большого конуса

OH — высота малого конуса

OA — радиус большого конуса

CH — радиус малого конуса

AS=SB=L

OC=OD=l

Задача

В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.

Дано:

Цилиндр вписан в конус

S_б.п.к.=15π дм

R=3дм

d_ц =l_ц

Найти r.

Решение:

AS=L — образующая конуса

KC=l — образующая цилиндра

AO=R – радиус основания конуса

KO=r — радиус цилиндра

πRL=15π

L=15π: (3π)=5

Рассмотрим подобные треугольники AKC и AOS.

В них: .

АО=3 (по условию)

KA=3-r

OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.

KC=2r

6r=4(3-r)

6r=12-4r

10r=12

r=1,2 (дм)

Ответ: r=1,2 (дм)

Примеры и разбор решения заданий тренировочного модуля

1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.

Решение:

Сделаем чертеж осевого сечения

Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.

Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.

Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.

Образующая конуса равна L=SA=R .

∆SHD∆DKB∆OSB — прямоугольные равнобедренные треугольники.

Радиус конуса R=OB=OK+KB.

OK=r, KB=h=2r.

Поэтому R=3r, образующая конуса равна SA=3r .

Выразим площади полных поверхностей конуса и цилиндра.

S_п.п.ц. =2πr(r+h)= 2πr(r+2r)=6πr².

S_п.п.к. =πR(R+L)= π3r(3r+3r)=9πr²(1+ )

Теперь найдем отношение: .

Ответ: .

2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.

Решение:

Сделаем чертеж осевого сечения:

O₁B — радиус меньшего основания усеченного конуса.

OC- радиус большего основания усеченного конуса и радиус цилиндра.

BH — высота цилиндра и высота усеченного конуса

По условию OC=2O₁B, ОС=16, BH=6.

Так как OC=2O₁B и ОС=16, то O₁B=8.

Рассмотрим треугольник BHC.

В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.

Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.

Найдем площадь боковой поверхности:

S_б.п.у.к. =πL(r+R)

S_б.п.у.к. =10π(8+16)=240π

Площадь полной поверхности найдем, прибавив две площади оснований:

S_п.п.у.к. =240π+64π+256π=560π

Ответ: S_п.п.у.к. =560π

Источник

1. Многогранник и шар

Шар вписан в призму, если он касается всех граней призмы.

Шар описан около призмы, если все вершины призмы лежат на поверхности шара.

Не во всякую призму можно вписать шар и не около всякой призмы можно описать шар.

Шар вписан в пирамиду, если он касается всех граней пирамиды.

Шар описан около пирамиды, если все вершины пирамиды лежат на поверхности шара.

2. Многогранник и цилиндр

Цилиндр вписан в прямую призму, если основания цилиндра вписаны в основания призмы.

Цилиндр описан около прямой призмы, если его основания описаны около оснований призмы.

Цилиндр вписан в пирамиду, если одно из его оснований принадлежит основанию пирамиды, а другое его основание вписано в сечение пирамиды плоскостью, параллельной ее основанию.

Цилиндр описан около пирамиды, если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра.

3. Многогранник и конус

Конус вписан в призму, если основание конуса вписано в одно из оснований призмы, а вершина конуса принадлежит другому основанию призмы.

Конус описан около призмы, если вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса.

Конус вписан в пирамиду, если основание конуса вписано в основание пирамиды, а вершина конуса совпадает с вершиной пирамиды.

Конус описан около пирамиды, если основание конуса описано около основания пирамиды, а вершина конуса совпадает с вершиной пирамиды.

4. Комбинация тел вращения

Шар вписан в конус, если он касается основания конуса в его центре, а боковой поверхности – по окружности. Центр шара находится на оси конуса и равноудален от центра основания и образующей конуса.

Шар описан около конуса, если вершина и окружность основания конуса лежат на поверхности шара. Центр шара лежит на прямой, содержащей ось конуса, и равноудален от вершины и точек окружности основания конуса.

Шар вписан в цилиндр, если он касается оснований цилиндра в их центрах, а боковой поверхности цилиндра по большой окружности шара, параллельной основаниям. Центр шара лежит на середине оси цилиндра, а радиус шара можно найти по формуле:

$LaTeX formula: R_{BPi }=frac{h}{2}$ , где – высота цилиндра.

Шар описан около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Не во всякий цилиндр можно вписать шар, но около всякого цилиндра можно описать шар.

При решении задач целесообразно строить вспомогательное сечение, проходящее через ось цилиндра или конуса и центр шара. При этом в сечении цилиндра будет получаться прямоугольник, в сечении конуса – равнобедренный треугольник, в сечении шара – круг с радиусом, равным радиусу шара.

Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра.

Конус описан около цилиндра, если одно из оснований цилиндра касается боковой поверхности конуса, а другое основание цилиндра принадлежит основанию конуса.

Пример 1. Шар радиуса касается всех граней прямоугольного параллелепипеда. Найдите объем шара, описанного около этого параллелепипеда.

Решение. Шар можем вписать только в прямоугольный параллелепипед, основание которого является квадрат (рис.9.78). Следовательно, имеем куб с ребром . Найдем диагональ этого куба: , .

Найдем радиус шара, описанного около куба: $LaTeX formula: R=frac{d}{2}=2sqrt{3}$ .

По формуле 9.26 найдем объем шара, описанного около куба: $LaTeX formula: V=frac{4}{3}pi 24sqrt{3}=32sqrt{3}pi$ .

Ответ: .

Пример 2. Все вершины треугольной призмы, основанием которой является треугольник со сторонами ; и , лежат на поверхности шара. Найдите объем шара, если высота призмы равна .

Решение. Так как шар описан около призмы, то все вершины призмы лежат на поверхности шара. Центр шара, с одной стороны, равноудален от вершин призмы, а с другой стороны, равноудален от центров окружностей, описанных около оснований призмы.

На рисунке 9.79: точки и – центры окружностей, описанных около оснований призмы; точка – центр шара; $LaTeX formula: R_{wapa}$ – радиус шара; .

Радиус окружности, описанной около основания призмы, найдем по формуле $LaTeX formula: R=frac{abc}{4S}$ .

Площадь основания призмы найдем по формуле Герона . Получим: .

Тогда $LaTeX formula: AO=R=frac{3cdot 3cdot 4}{4cdot 2sqrt{5}}=frac{9}{2sqrt{5}}$ .

По теореме Пифагора: $LaTeX formula: R^2_{wapa}=AO^2+PO^2$ , $LaTeX formula: R^2_{wapa}=frac{81}{20}+16=frac{401}{20}$ .

Площадь поверхности шара найдем по формуле 9.25 : $LaTeX formula: S=frac{4pi cdot 401}{20}=80,2pi$ .

Ответ: .

Пример 3. Найдите отношение радиуса шара, описанного около правильного тетраэдра, к радиусу шара, вписанного в этот тетраэдр.

Решение. Пусть ребро тетраэдра равно . Высота правильного тетраэдра опускается в центр правильного треугольника (рис. 9.80), поэтому $LaTeX formula: OA=R=frac{a}{sqrt{3}}$ , $LaTeX formula: OD=r=frac{a}{2sqrt{3}}$ . Центры описанного около правильного тетраэдра и вписанного в него шаров совпадают и лежат на высоте тетраэдра (точка ).

Поскольку точки , , и лежат на поверхности шара, то $LaTeX formula: O_1A=O_1C=O_1B=O_1S=R_{Onuc.}$

Угол – угол наклона боковой грани к плоскости основания ( и – перпендикуляры к ребру ).

Вписанный шар касается всех граней тетраэдра, следовательно, его радиус является перпендикуляром к плоскостям граней, то есть $LaTeX formula: R_{Bnuc.}=O_1O=O_1N$ .

Так как ( $LaTeX formula: angle SNO_1=angle SOD=90^{circ}$ и — общий), то запишем $LaTeX formula: frac{OD}{NO_1}=frac{SD}{SO_1}$ или $LaTeX formula: frac{r}{R_{Bnuc.}}=frac{SD}{R_{Onuc.}}$ , откуда $LaTeX formula: R_{Onuc.}=frac{R_{Bnuc.}cdot SD}{r}$ .

Длину отрезка найдем из теоремы Пифагора: $LaTeX formula: CD=sqrt{a^2-frac{a^2}{4}}=frac{asqrt{3}}{2}$ .

Найдем отношение радиусов описного около тетраэдра и вписанного в тетраэдр шаров:

$LaTeX formula: frac{R_{Onuc.}}{R_{Bnuc.}}=frac{R_{Bnuc.}cdot SD}{rcdot R_{Bnuc.} }=frac{SD}{r}=frac{asqrt{3}}{2}:frac{a}{2sqrt{3}}=frac{asqrt{3}cdot 2sqrt{3}}{2a}=3$ .

Ответ: .

Пример 4. В прямой параллелепипед, одна из диагоналей оснований которого равна и равна стороне основания, вписан цилиндр, высота которого равна . Найдите объем параллелепипеда.

Решение. Окружность можно вписать в квадрат или в ромб. Но диагональ квадрата не может быть равна его стороне. Диагональ ромба может быть равна его стороне, если угол ромба равен $LaTeX formula: 60^{circ}$ . Следовательно, основание параллелепипеда – ромб.

Согласно формуле найдем площадь ромба:

$LaTeX formula: S=12cdot frac{sqrt{3}}{2}=6sqrt{3}$ .

Высота параллелепипеда равна высоте цилиндра: .

Согласно формуле 9.6 найдем объем параллелепипеда:

Ответ: .

Пример 5. Около правильной треугольной пирамиды описан цилиндр, объем которого равен . Найдите объем пирамиды.

Решение. Пусть – радиус основания цилиндра, – высота цилиндра и пирамиды.

Согласно формулам 9.15 и 9.16 запишем: $LaTeX formula: pi R^2h=12sqrt{3}pi$ , $LaTeX formula: R^2h=12sqrt{3}$ .

Так как основание пирамиды – правильный треугольник со стороной , а – радиус окружности, описанной около этого треугольника, то .

Найдем площадь основания пирамиды: $LaTeX formula: S_{o.}=frac{sqrt{3}a^2}{4}=frac{3sqrt{3}R^2}{4}$ .

Согласно формуле 9.11 запишем объем пирамиды: $LaTeX formula: V=frac{1}{3cdot }frac{3sqrt{3}R^2}{4}cdot h=frac{sqrt{3}}{4}cdot R^2h$ . Учитывая, что $LaTeX formula: R^2h=12sqrt{3}$ , получим: $LaTeX formula: V=frac{sqrt{3}}{4}cdot 12sqrt{3}=9$ .

Ответ: .

Пример 6. Конус вписан в треугольную призму, основанием которой является прямоугольный треугольник с катетами см и см, а высота равна см. Найдите площадь боковой поверхности конуса (рис. 9.81).

Решение. 1. Найдем гипотенузу треугольника: (см).

2. Найдем радиус окружности, вписанной в основание призмы:

$LaTeX formula: r=frac{a+b-c}{2}$ , $LaTeX formula: r=frac{5+12-13}{2}=2$ (см).

3. Высота конуса равна высоте призмы: см.

4. По теореме Пифагора найдем образующую конуса:

$LaTeX formula: l=sqrt{r^2+h^2}$ , .

5. По формуле 9.22 найдем боковую поверхность конуса: ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^2$ .

Пример 7. Правильная шестиугольная пирамида вписана в конус, объем которого равен $LaTeX formula: frac{16pi }{3}$ . Найдите площадь боковой поверхности пирамиды, если известно, что радиус основания конуса в два раза меньше его высоты.

Решение. На рисунке 9.82: – высота конуса и высота пирамиды, – радиус основания конуса и радиус окружности, описанной около правильного шестиугольника и .

С учетом формул 9.19 и 9.20 получим: $LaTeX formula: frac{16pi }{3}=frac{1}{3}pi R^2cdot 2R$ , откуда , . Тогда: сторона правильного шестиугольника равна ; .

Найдем радиус окружности, вписанной в шестиугольник: $LaTeX formula: r=frac{3sqrt{3}a^2}{2}$ , $LaTeX formula: r=frac{3sqrt{3}cdot 4}{2}=6sqrt{3}$ .

По теореме Пифагора найдем апофему пирамиды:

$LaTeX formula: CS=sqrt{h^2+r^2}=sqrt{1+108}=sqrt{109}$ .

По формуле 9.13 найдем площадь боковой поверхности пирамиды:

$LaTeX formula: S=frac{1}{2}P_{o.}cdot h_{delta .}$ , $LaTeX formula: S=frac{1}{2}cdot 12cdot sqrt{109}=6sqrt{109}$ .

Ответ: .

Пример 8. Конус, высота которого равна , вписан в шар радиуса . Найдите объем конуса.

Решение. На рисунке 9.83 построено осевое сечение конуса. Так как , а , то .

По теореме Пифагора: . По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}pi r^2h=frac{pi}{3}(2sqrt{3})^2cdot 6=24pi$ .

Ответ: .

Пример 9. В конус, осевое сечение которого – равносторонний треугольник, вписан шар. Найдите объем конуса, если объем шара равен $LaTeX formula: frac{9pi }{16}$ $LaTeX formula: _{CM}\^3$ .

Решение. Объем шара находят по формуле 9.26 . Радиус шара найдем, решая уравнение $LaTeX formula: frac{4}{3}pi R^3_{wapa}=frac{9pi}{16}$ , откуда получим $LaTeX formula: R_{wapa}=frac{3}{4}$ см. Так как осевым сечением конуса является равносторонний треугольник (рис. 9.84), то центр шара (точка ) лежит на высоте конуса и радиус шара равен радиусу окружности, вписанной в треугольник , т. е. $LaTeX formula: R_{wapa}=r$ .

В свою очередь радиус окружности, вписанной в правильный треугольник со стороной , находят по формуле $LaTeX formula: r=frac{a}{2sqrt{3}}$ . Следовательно, , $LaTeX formula: a=2sqrt{3}cdot frac{3}{4}=frac{3sqrt{3}}{2}$ (см).

Найдем радиус основания конуса и его высоту: $LaTeX formula: R_{kappa .}=frac{1}{2}cdot a=frac{3sqrt{3}}{2}$ (см); $LaTeX formula: h_{kappa .}=sqrt{a^2-frac{a^2}{4}}=frac{sqrt{3}a}{2}$ , $LaTeX formula: h_{kappa .}=frac{sqrt{3}}{2}cdot frac{3sqrt{3}}{2}=frac{9}{4}$ (см).

Согласно формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}pi left ( frac{3sqrt{3}}{2} right )^2cdot frac{9}{4}=frac{81pi}{64}$ ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: frac{81pi}{64}$ $LaTeX formula: _{CM}\^3$ .

Пример 10. В цилиндр, площадь поверхности которого равна , вписана сфера. Найдите площадь поверхности сферы.

Решение. Осевое сечение цилиндра – квадрат. Тогда, если радиус основания цилиндра , то его образующая и радиус шара .

Согласно условию задачи: , , , , , .

Тогда и согласно формуле 9.25 получим: $LaTeX formula: S_{cphi .}=4pi sqrt{2}^2=8pi$ .

Ответ: .

1. В любую треугольную пирамиду можно вписать шар и около любой треугольной пирамиды можно описать шар.

2. В любой конус можно вписать шар и около любого конуса можно описать шар.

3. Решая задачи стереометрии, часто вовсе не обязательно изображать сами пространственные фигуры, а достаточно лишь выполнить некоторые фрагменты рисунка.

Объем прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.6)

Площадь поверхности прямой призмы находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.7)

Площадь боковой поверхности прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: S_{delta .}=P_{o.} cdot h$ . (9.8)

Объем наклонной призмы можно вычислить по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.9)

Площадь поверхности наклонной призмы можно вычислить по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ , (9.10)

Объем пирамиды высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.} cdot h$ , (9.11)

Площадь поверхности пирамиды находят по формуле:

$LaTeX formula: S_{n.}=S_{o.}+S_{delta .}$ . (9.12)

Площадь боковой поверхности правильной пирамиды находят по формуле:

$LaTeX formula: S_{delta .}=frac{1}{2}P_{o.} cdot h_{delta .}$ , (9.13)

где $LaTeX formula: h_{delta .}$ – апофема пирамиды.

Объем цилиндра высоты находят по формуле:

$LaTeX formula: V=S_{o.}cdot h$ . (9.15)

Площадь основания цилиндра ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r ^2$ . (9.16)

Площадь поверхности цилиндра находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.17)

Площадь боковой поверхности цилиндра находят по формуле:

$LaTeX formula: S_{delta .}=2pi r l$ , (9.18)

где – радиус основания, – высота, – образующая цилиндра.

Объем конуса высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.}cdot h$ . (9.19)

Площадь основания конуса ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r^2$ . (9.20)

Площадь поверхности конуса находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.21)

Площадь боковой поверхности конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi r l$ , (9.22)

где r – радиус основания, l – образующая конуса.

Площадь сферы радиуса находят по формуле:

$LaTeX formula: S_{cphi .}=4pi R^2$ . (9.25)

Объем шара радиуса находят по формуле:

$LaTeX formula: V_{wapa}=frac{4}{3}pi R^3$ . (9.26)

Источник

Формулы объема и площади поверхности. Цилиндр, конус и шар

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.

(ведь 2^2=4 , 2^3=8 ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в sqrt{2} раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких sqrt{2} или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Формулы объема и площади поверхности. Цилиндр, конус и шар» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник