Как найти объем цилиндра вписанного в призму - Исправление недочетов и поиск решений вместе с Examum.ru

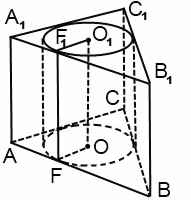
Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.

Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.

Например, цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.

Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т. к. высота призмы равна высоте цилиндра.

Окружность основания цилиндра описана около многоугольника основания призмы.

Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны

180°

Формулы вычисления радиуса (R) описанной окружности

(a, b, c) — стороны, (h) — высота, (d) — диагональ.

Правильный треугольник	(R =) 23h; (R=) a33
Прямоугольный треугольник	(R=) 12 гипотенузы
Произвольный треугольник	R=abc4S;R=a2sinα
Квадрат	(R =) a22
Прямоугольник	(R =) d2
Правильный шестиугольник	(R = a)

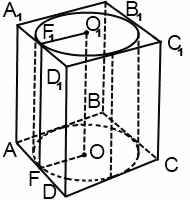
Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.

Например, цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.

Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.

Окружность основания цилиндра вписана в многоугольник основания призмы.

Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.

Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.

Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.

Формулы вычисления радиуса (r) вписанной окружности

Где (h) — высота, (S) — площадь, (p) — полупериметр, (a) — сторона.

Правильный треугольник	r=13h;r=a36
Произвольный (и прямоугольный) треугольник	(r =) Sp
Квадрат
Ромб	или
Правильный шестиугольник	(r =) a32

Источник

Необходимо запомнить.

ВАЖНО!

Объем прямой призмы. Объем цилиндра

Объем прямой призмы равен произведению ее площади основания на высоту: V_пр.пр= S_осн∙ h

Цилиндр называется вписанным в призму, если его основания вписаны в основания призмы, и наоборот, описанным – если основания описаны около оснований цилиндра. Высоты у призмы и вписанного, и описанного, цилиндров совпадают.

Объем цилиндра равен произведению площади основания на высоту. V_цил= S_осн∙ h

V = πR²H, где R – радиус основания, Н – высота цилиндра, π≈3,14

l = 2πR, где R – радиус окружности, l – длина окружности.

Источник

Призма описана около цилиндра, если ее основания — многоугольники, описанные около оснований цилиндра. Соответственно, цилиндр вписан в призму.

Цилиндр можно вписать в призму, если в основание призмы можно вписать окружность. Радиус вписанной окружности равен радиусу цилиндра. Высоты цилиндра и призмы равны. В школьном курсе изучается только прямой круговой цилиндр, соответственно, цилиндр в этом случае вписан в прямую призму.

Боковые грани описанной около цилиндра призмы являются касательными плоскостями к боковой поверхности цилиндра.

Найдем отношение объема призмы к объему вписанного в нее цилиндра:

$[frac{{{V_1}}}{{{V_2}}} = frac{{{S_{ocn}} cdot H}}{{pi {r^2}H}} = frac{{prH}}{{pi {r^2}H}} = frac{p}{{pi r}}.]$

p — полупериметр основания призмы, r — радиус вписанной в основание призмы окружности и радиус цилиндра, H — высота призмы и высота цилиндра.

В частности, отношение объема правильной треугольной призмы к объему вписанного цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{p}{{pi r}} = frac{{frac{{3a}}{2}}}{{pi cdot frac{a}{{2sqrt 3 }}}} = frac{{3sqrt 3 }}{pi }.]$

Отношение объема правильной четырехугольной призмы к объему вписанного цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{p}{{pi r}} = frac{{2a}}{{pi cdot frac{a}{2}}} = frac{4}{pi }.]$

Для правильной шестиугольной призмы это отношение равно

$[frac{{{V_1}}}{{{V_2}}} = frac{p}{{pi r}} = frac{{3a}}{{pi cdot frac{{asqrt 3 }}{2}}} = frac{6}{{pi sqrt 3 }} = frac{{2sqrt 3 }}{pi }.]$

Отношение площади боковой поверхности призмы к боковой поверхности вписанного цилиндра:

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}} cdot H}}{{2pi rH}} = frac{{{P_{ocn}}}}{{2pi r}}.]$

Поскольку половина периметра основания — полупериметр,

$[frac{{{P_{ocn}}}}{2} = p, Rightarrow frac{{{S_1}}}{{{S_2}}} = frac{p}{{pi r}}.]$

Таким образом, если цилиндр вписан в призму, отношение площади боковой поверхности призмы к боковой поверхности цилиндра равно отношению объема призмы к объему вписанного цилиндра. В частности, отношение площади боковой поверхности правильной треугольной призмы к площади боковой поверхности вписанного цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi r}} = frac{{3a}}{{2pi cdot frac{a}{{2sqrt 3 }}}} = frac{{3sqrt 3 }}{pi }.]$

Отношение боковой поверхности правильной четырехугольной призмы к боковой поверхности вписанного цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi r}} = frac{{4a}}{{2pi cdot frac{a}{2}}} = frac{4}{pi }.]$

Отношение боковой поверхности правильной шестиугольной призмы к боковой поверхности вписанного цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi r}} = frac{{6a}}{{2pi cdot frac{{asqrt 3 }}{2}}} = frac{6}{{pi sqrt 3 }} = frac{{2sqrt 3 }}{pi }.]$

При решении задач, в которых цилиндр вписан в призму, можно рассматривать часть сечения комбинации тел плоскостью, проходящей через ось цилиндра. Для прямой призмы это сечение — прямоугольник, стороны которого равны радиусу цилиндра и высоте цилиндра. Например, AA1O1O: AA1=H, AO=r.

Источник

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

похожие вопросы 5

Источник