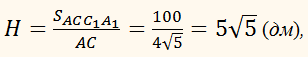| 1. |
Вычисление объёма по формуле
Сложность: |
1 |
| 2. |
Объём по площади основания
Сложность: |
1 |
| 3. |
Площадь боковой грани
Сложность: |
2 |
| 4. |
Вычисление длины ряда кубиков
Сложность: |
2 |
| 5. |
Вычисление суммы объёмов
Сложность: |
2 |
| 6. |
Угол между диагональю основания и стороной основания
Сложность: |
2 |
| 7. |
Выражение с переменной
Сложность: |
2 |
| 8. |
Отношение измерений прямоугольного параллелепипеда
Сложность: |
3 |
| 9. |
Вычисление высоты
Сложность: |
2 |
| 10. |
Диагонали диагонального сечения
Сложность: |
3 |
| 11. |
Площадь сечения
Сложность: |
3 |
| 12. |
Площадь диагонального сечения
Сложность: |
3 |
| 13. |
Диагонали граней
Сложность: |
3 |
| 14. |
Диагональ, площадь поверхности и объём куба
Сложность: |
3 |
| 15. |
Вычисление наибольшего объёма
Сложность: |
1 |
| 16. |
Определение максимального объёма
Сложность: |
5 |
| 17. |
Чертёж детали
Сложность: |
4 |
Подождите!
Не закрывайте страницу. Нейросеть пишет ответ. Он появится тут.
Этот ответ написан нейросетью.
Искуственный интеллект во многом преуспевает, но в некоторых областях может давать неточные ответы.
Если вам не понравился ответ, попробуйте задать его более развёрнуто и конкретно, используя точные параметры.
Ответ нейросети:
Для начала обозначим длину стороны прямоугольного параллелепипеда, параллельной диагонали диагонального сечения, как l. Тогда, по условию, имеем AB = l√2.
Также из условия задачи известно, что ААт = 11 м = 1100 см. Следовательно, диагональ диагонального сечения параллелепипеда равна DC = 1100 – 2 = 1098 см.
Используя теорему Пифагора для прямоугольного треугольника ABC, получаем:
AC² + BC² = AB²,
(l√2)² + l² = AB²,
2l² + l² = AB²,
l² = (1/3) AB².
Таким образом, l = AB/√3 = 2/√3 см.
Объем параллелепипеда равен произведению длин его трех сторон, то есть:
V = AB·AC·AD
= 2·(l√2)·(l√3)
= 2l³√6
= 8√2/3 см³.
Ответ: объем равен 8√2/3 см³.
⚠️Зарепортить пост!
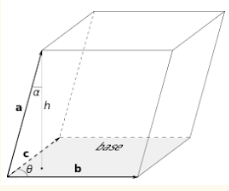
Объём наклонного параллелепипеда равен произведению площади
его основания на высоту.
где Sосн –
площадь основания наклонного параллелепипеда, h – высота наклонного параллелепипеда.
ЗАДАЧА:
Основанием наклонного параллелепипеда
является параллелограмм АВСD,
у которого АВ =
3 дм, АD = 7 дм и ВD = 6
дм. Диагональное сечение АА1С1С перпендикулярно к плоскости основания и его
площадь равна 1 м2. Найдите объём параллелепипеда.
РЕШЕНИЕ:
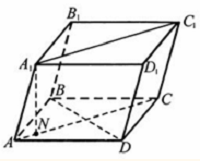
Пусть имеем наклонный параллелепипед АВСDА1В1С1D1, в
котором плоскость диагонального сечения АСС1А1 перпендикулярна к плоскости основания.
Кроме того, по условию,
АВ =
3 дм, АD = 7 дм, ВD = 6 дм,
За свойством сторон и диагоналей паралелограма
AC2 + BD2 = 2(AB2 + AD2),
откуда:
AC2 = 2(9 + 49) – 36 =
80,
AC = 4√͞͞͞͞͞5 (дм).
Проведем высоту A1N = H
параллелепипеда (N∈AC) и найдём
её из параллелограмма АСС1А1:
Sосн = 2S∆ABD.
Площадь треугольника ABD найдём по формуле
Герона:
p = 1/2(3 + 7 + 6) = 8 (дм),
Поэтому
Sосн = 8√͞͞͞͞͞5 (дм3).
V = Sосн × H = 8√͞͞͞͞͞5 × 5√͞͞͞͞͞5
= 200 (дм3) = 0,2 (м3).
ОТВЕТ:
0,2 м3.
ЗАДАЧА:
Площадь боковой грани треугольной
призмы равна S,
а расстояние от противоположного ребра до этой грани а. Найдите
объём призмы.
РЕШЕНИЕ:
Пусть имеем наклонную треугольную
призму АВСА1В1С1, площадь её боковой грани ВСС1В1 равна S,
а d(AA1; (BCC1)) = а. Объём этой призмы
обозначим как V. Достроим
данную треугольную призму до параллелепипеда АВСDА1В1С1D1.
Объём такого параллелепипеда
вдвое больше за объём данной призмы, то есть равен 2V. Рассмотрим
за основание призмы АВСDА1В1С1D1 грань ВСС1В1. Тогда її объём равен
2V = S ×
d(AA1; (BCC1)) = S
× а.
ОТВЕТ: 1/2 S
×
а.
ЗАДАЧА:
Основанием параллелепипеда является ромб со стороной 4 и острым углом 60°. Одно из рёбер параллелепипеда составляет с этой гранью
угол в 60° и равно
5. Найдите объём параллелепипеда.
РЕШЕНИЕ:
Начертим чертёж.
Объём параллелепипеда находим по следующей формуле:
V = So ∙ H,
где Н – высота параллелепипеда.
Площадь ромба с заданной стороной a и углом
α,
находим по следующей формуле:
So = a2 ∙ sin α.
Подставляя известные величины, получаем:
So = a2 ∙ sin α = 16∙1/2∙√͞͞͞͞͞3 = 8√͞͞͞͞͞3.
Угол между ребром АА1 и гранью
основания АВСD –
есть угол между этим ребром и проекцией ребра на плоскость основания, которая равна АН,
где Н –
проекция точки А1 на АВСD, то
есть
∠ А1АН = 60°.
В прямоугольном
треугольнике АА1Н:
Задания к уроку 6
Примечание. Текст задачи взят с форума
Задача.
Диагональным сечением правильной четырехугольной призмы является квадрат, площадь которого равен 144 квадратных сантиметров.
Найдите объем объем призмы.
Решение.
Поскольку, согласно определению диагонального сечения призмы, оно проходит через диагональ основания, а данная призма является правильной и четырехугольной, то данное диагональное сечение проходит через диагональ основания, которое является квадратом.
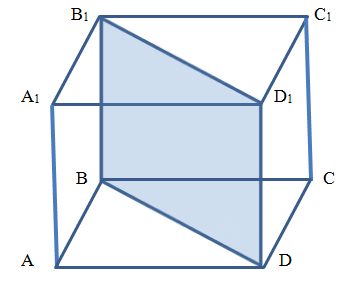
Исходя из того, что площадь диагонального сечения является квадратом (BB1DD1), то сторона квадрата (она же равна высоте призмы) равна:
а = √144 = 12 см
Как мы уже показали, в основании данной призмы также лежит квадрат ABCD, диагональ которого мы только что определили.
Таким образом, если обозначить сторону квадрата как b, получим:
b2 + b2 = 122
или
2b2 = 144
b2 = 72
Заметим, что площадь основания (квадрата ABCD) равна
S = b2
то есть
S = 72
Согласно формуле нахождения объема призмы
V = Sh
Подставим значения:
V = 72h
высота сечения равна высоте прямой призмы и это значение было найдено нами ранее, то есть
V = 72 * 12 = 864 см3
Ответ: 864 кубических сантиметра
0
Куб |
Описание курса
| Параллепипед
Размещено 3 года назад по предмету
Математика
от ficus2
-
Ответ на вопрос
Ответ на вопрос дан
okneretПрименены: формула объёма прямоугольного параллелепипеда, теорема Пифагора, формула площади прямоугольника
-
Ответ на вопрос
Ответ на вопрос дан
ficus2 -
Ответ на вопрос
Ответ на вопрос дан
ficus2 -
Ответ на вопрос
Ответ на вопрос дан
okneretВ первой строчке решения: 1365
-
Ответ на вопрос
Ответ на вопрос дан
ficus2 -
Ответ на вопрос
Ответ на вопрос дан
okneretВ данном случае площадь прямоугольника*высоту то же самое, что и a*b*c
-
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.