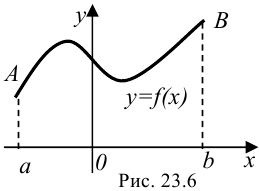
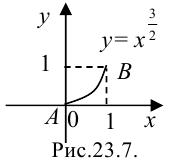
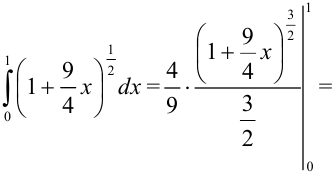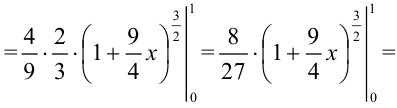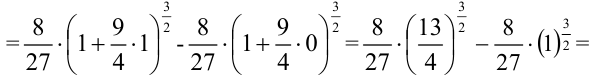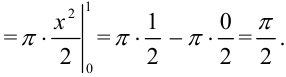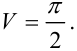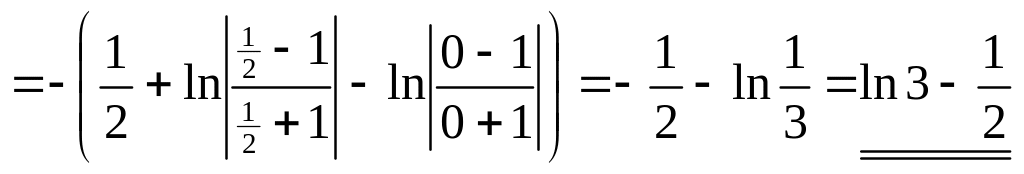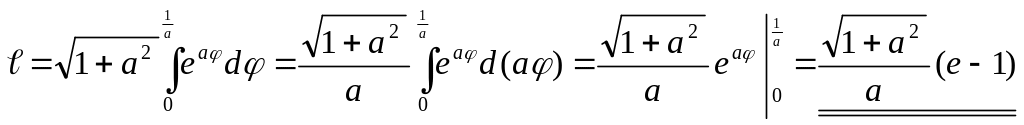Рассмотрим функцию 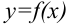
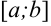
1. Длина дуги 
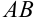
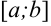
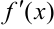
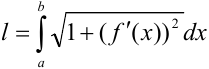
Пример №23.3.
Найдите длину дуги линии 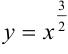
Решение:
Для вычисления длины дуги 
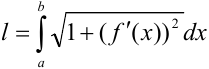
В качестве 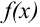
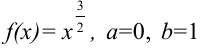
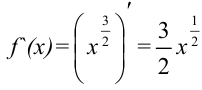
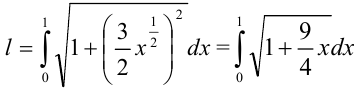
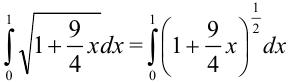
Ответ: 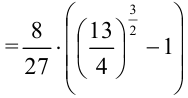
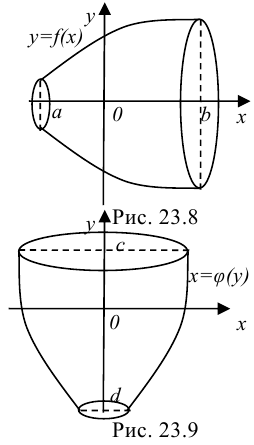
2. Объем тела вращения, полученного вращением вокруг оси 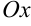
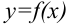
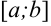
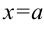
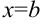
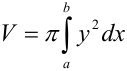
Объем тела вращения, полученного вращением вокруг оси 
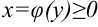
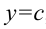
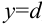
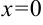
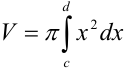
Пример №23.4.
Найдите объем тела, полученного вращением вокруг оси 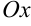
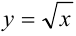
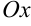
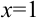
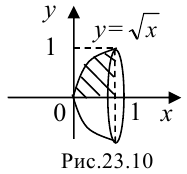
Решение:
Построим фигуру, ограниченную графиком функции 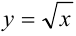
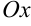
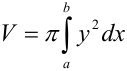
В нашем примере 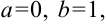
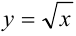
Ответ:
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
Слайд 1Вычисление длин дуг. Вычисление объемов тел по
площадям поперечных сечений. Вычисление объемов тел вращения.
Несобственные интегралы.
Лекция 10

Слайд 2О1
Под длиной дуги АВ понимается предел, к
которому стремится длина ломаной линии, вписанной в
эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена ее стремится к нулю.
О2
Кривая называется гладкой, если она непрерывна и в каждой точке имеет касательную, непрерывно меняющую свое положение от точки к точке.
Кривая задана уравнением (1) f’(x) – непрерывна на отрезке [a,b].
Теорема Всякая гладкая кривая (1) имеет определенную конечную длину дуги.

Слайд 3Док-во:
Впишем в данную гладкую кривую (1) ломаную
линию
Проектируя звенья ломаной на ось ОХ, получим разбиение отрезка [a,b] на систему отрезков . Пусть — приращение функции y=f(x) на отрезке [a,b]. По теореме Пифагора имеем . Применяя теорему Лагранжа о конечном приращении функции, получим , где — некоторая промежуточная точка отрезка . Отсюда . Длина всей ломаной линии (то есть ее периметр) равна
. Для нахождения длины L кривой (1) в последнем
выражении переходим к пределу при
и . Таким образом
Получаем предел
интегральной суммы для
непрерывной функции
Поэтому или
(2), где y’=f’(x)

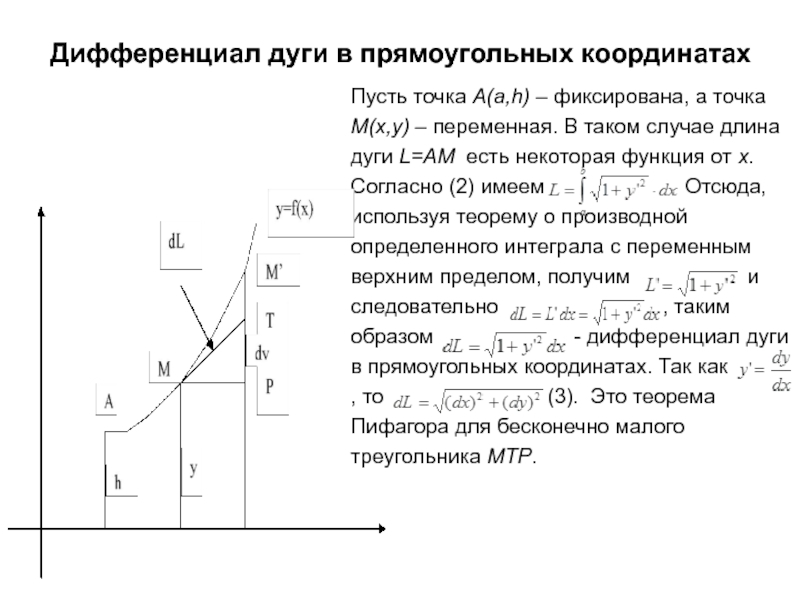
Слайд 4Дифференциал дуги в прямоугольных координатах
Пусть точка A(a,h)
– фиксирована, а точка M(x,y) – переменная.
В таком случае длина дуги L=AM есть некоторая функция от х. Согласно (2) имеем Отсюда, используя теорему о производной определенного интеграла с переменным верхним пределом, получим и следовательно , таким образом — дифференциал дуги в прямоугольных координатах. Так как , то (3). Это теорема Пифагора для бесконечно малого треугольника MTP.
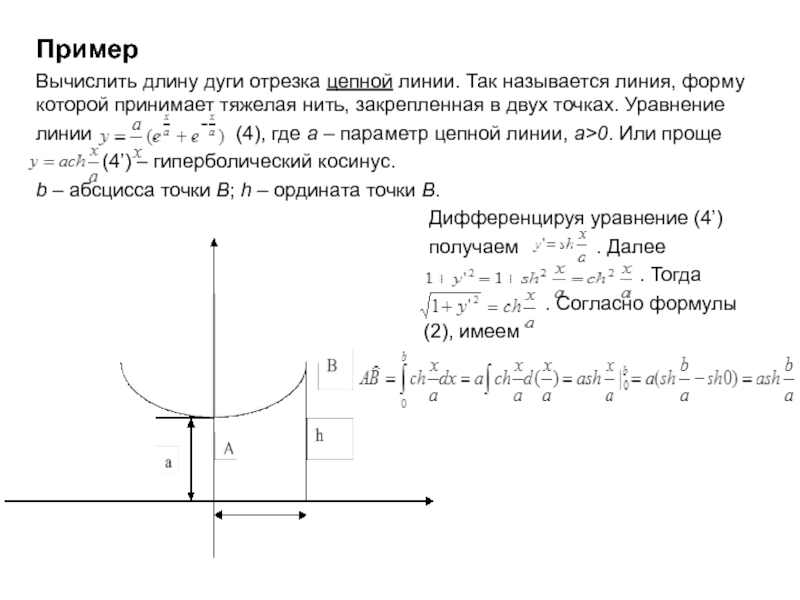
Слайд 5Пример
Вычислить длину дуги отрезка цепной линии. Так
называется линия, форму которой принимает тяжелая нить,
закрепленная в двух точках. Уравнение
линии (4), где а – параметр цепной линии, а>0. Или проще
(4’) – гиперболический косинус.
b – абсцисса точки В; h – ордината точки В.
Дифференцируя уравнение (4’)
получаем . Далее
. Тогда
. Согласно формулы
(2), имеем
Слайд 6Нахождение длины дуги кривой, заданной параметрическими уравнениями
Пусть
L – длина дуги кривой
, , —
непрерывно дифференцируемые функции на заданном отрезке.
Формула (3) для дифференциала дуги справедлива и в этом случае dx=x’dt; dy=y’dt. Имеем
Интегрируя последнее выражение в пределах от до t=T получим длину дуги (5)
Пример
Найти длину дуги окружности, заданной параметрическими уравнениями
от t=0 до t=T
Решение
Здесь dx=-asintdt; dy=acostdt. Поэтому и,
следовательно

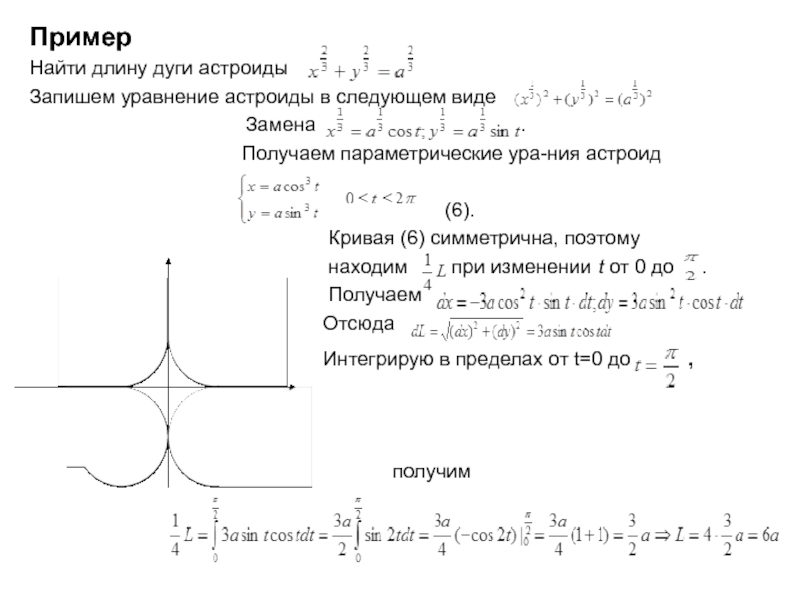
Слайд 7Пример
Найти длину дуги астроиды
Запишем уравнение астроиды
в следующем виде
Замена .
Получаем параметрические ура-ния астроид
(6).
Кривая (6) симметрична, поэтому
находим при изменении t от 0 до .
Получаем .
Отсюда .
Интегрирую в пределах от t=0 до ,
получим
Слайд 8Длина дуги в полярных координатах
Выведем сначала формулу
для дифференциала dL дуги в полярных координатах
на основании формулы (3)
, где x,y – прямоугольные декартовы координаты точки дуги.
Формулы перехода:
Отсюда , следовательно или
(1), где
Задача
Найти длину дуги L непрерывно дифференцируемой кривой между точками и , где — полярные координаты.
Интегрируя равенство (1) в пределах от до
получаем длину дуги в полярных
координатах , где
— производная

Слайд 9Пример
Вычислить полную длину дуги кардиоиды
Решение
Имеем

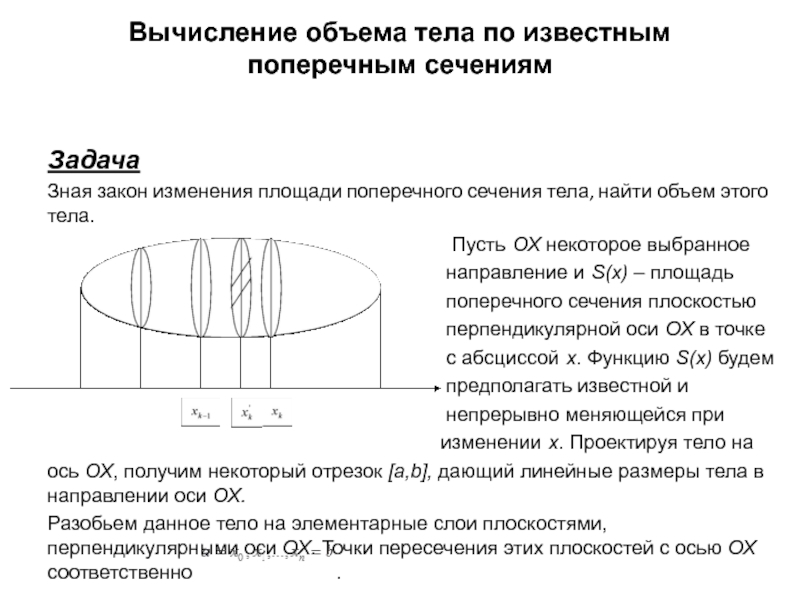
Слайд 10Вычисление объема тела по известным поперечным сечениям
Задача
Зная
закон изменения площади поперечного сечения тела, найти
объем этого тела.
Пусть ОХ некоторое выбранное
направление и S(x) – площадь
поперечного сечения плоскостью
перпендикулярной оси ОХ в точке
с абсциссой х. Функцию S(x) будем
предполагать известной и
непрерывно меняющейся при
изменении х. Проектируя тело на
ось ОХ, получим некоторый отрезок [a,b], дающий линейные размеры тела в направлении оси ОХ.
Разобьем данное тело на элементарные слои плоскостями, перпендикулярными оси ОХ. Точки пересечения этих плоскостей с осью ОХ соответственно .
Слайд 11 Каждый элементарный слой, ограниченный плоскостями, пересекающимися
в точках
заменяем цилиндром с высотой и площадью основания . Объем данного цилиндра выражается формулой . Составим сумму всех таких
произведений . Эта сумма является интегральной для
данной функции S=S(x) на отрезке [a,b]. Она выражает объем ступенчатого тела, состоящего их элементарных цилиндров и приближенно заменяющего данное тело.
Объемом тела называют предел объема указанного ступенчатого тела, приближенно заменяющего данное тело, при — длина наибольшего из элементарных отрезков .
По определению с другой стороны . Из
двух последних равенств получаем формулу вычисления объема тела по заданным поперечным сечениям.
(1)

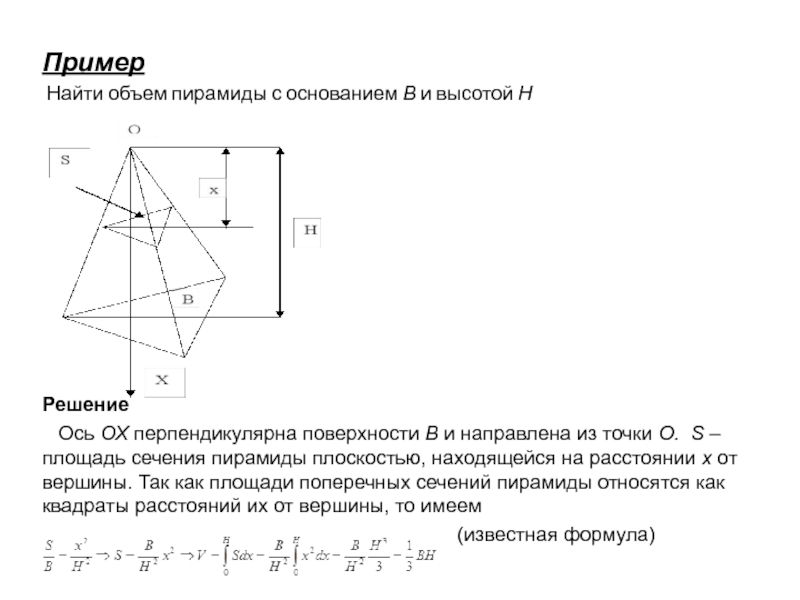
Слайд 12Пример
Найти объем пирамиды с основанием В
и высотой Н
Решение
Ось ОХ перпендикулярна
поверхности В и направлена из точки О. S – площадь сечения пирамиды плоскостью, находящейся на расстоянии х от вершины. Так как площади поперечных сечений пирамиды относятся как квадраты расстояний их от вершины, то имеем
(известная формула)
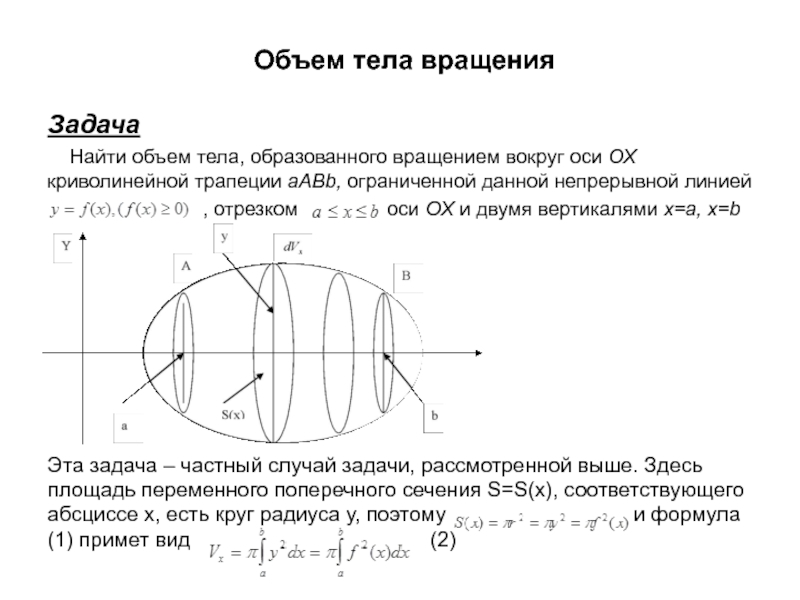
Слайд 13Объем тела вращения
Задача
Найти объем тела,
образованного вращением вокруг оси ОХ криволинейной трапеции
aABb, ограниченной данной непрерывной линией
, отрезком оси ОХ и двумя вертикалями x=a, x=b
Эта задача – частный случай задачи, рассмотренной выше. Здесь площадь переменного поперечного сечения S=S(x), соответствующего абсциссе х, есть круг радиуса у, поэтому и формула (1) примет вид (2)
Слайд 14Задача
Найти объем тела, образованного вращением
вокруг оси ОУ криволинейной трапеции cCDd, ограниченной
данной непрерывной линией , отрезком оси ОУ и двумя горизонталями y=c, y=d
По аналогии с формулой (2)
(3)
Примеры
1. Вычислить объем тела, полученного вращением вокруг
оси ОХ криволинейной трапеции, ограниченной линиями
Решение
Пределы интегрирования a=1,b=6, функция
2. Вычислить объем тела, полученного в результате вращения вокруг оси ОХ криволинейной трапеции, ограниченной линией , осями координат и прямой х=1
Решение
Пределы интегрирования a=0,b=1, функция

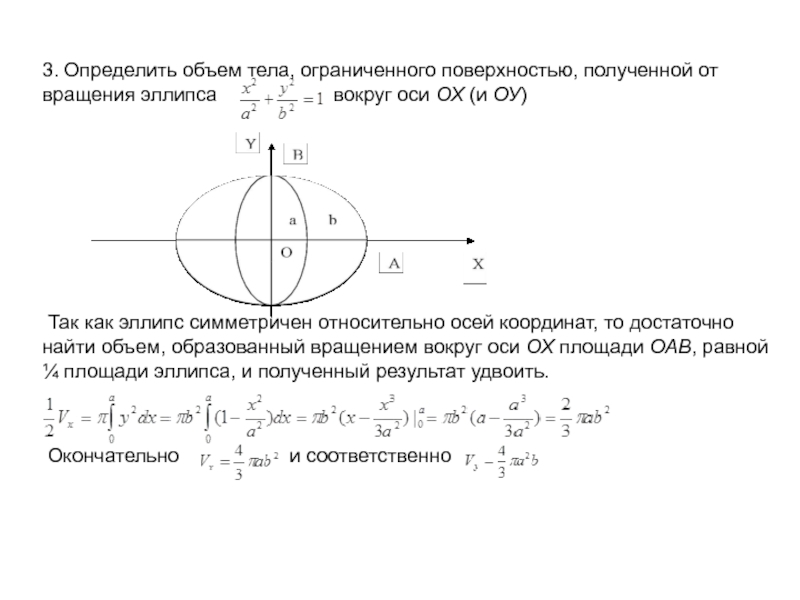
Слайд 153. Определить объем тела, ограниченного поверхностью, полученной
от вращения эллипса
вокруг оси ОХ (и ОУ)
Так как эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси ОХ площади ОАВ, равной ¼ площади эллипса, и полученный результат удвоить.
Окончательно и соответственно
Слайд 16Несобственные интегралы
При определении интеграла
(1) предполагалось, что:
1) Отрезок интегрирования [a,b] – конечен;
2) f(x) определена и непрерывна на отрезке [a,b].
Такой определенный интеграл называется собственным (название опускается).
Если нарушается по крайней мере одно из двух условий 1) или 2), то (1) называется несобственным определенным интегралом.
Рассмотрим смысл этого понятия для двух простейших случаев
Пусть f(x) непрерывна при . Тогда по определению полагают
(2)
Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), называется сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.

Слайд 17Геометрическая интерпретация
Геометрически для неотрицательной на
функции f(x) несобственный интеграл (2)
представляет собой площадь
криволинейной фигуры, ограниченной
данной линией y=f(x), осью
ОХ и вертикалью х=а.
Пусть F(x) первообразная для f(x). На основании формулы (2) имеем
. Если ввести условное обозначение
, то получим для сходящегося несобственного интеграла с бесконечным верхним пределом обобщенную формулы Ньютона-Лейбница
(3), где F’(x)=f(x).
Примеры
1)
2) Установить, при каких значениях интеграл сходится и при каких расходится

Слайд 18Решение Так как при
,
то
. Следовательно , можно сделать следующие выводы:
Если , то — интеграл сходится;
Если , то — интеграл расходится;
Если , то — интеграл расходится;
3.Вычислить (второй интеграл равен (см. Пример 1)).
Вычислим
следовательно
Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, оценить его значение. Для этого могут быть полезны следующие теоремы.
Теорема 1
Если для любого х выполняется неравенство и если сходится, то также сходится , при этом

Слайд 19 4. Исследовать, сходится ли интеграл
Решение
При
сходится и его значение меньше или равно 1.
Теорема 2
Если для любого х выполняется неравенство и если
расходится, то также расходится.
5. Исследовать, сходится ли интеграл
Решение
При следовательно расходится и данный интеграл.
Для функции меняющий знак в бесконечном интервале, имеет место следующая теорема.
Теорема 3
Если интеграл сходится, то сходится и интеграл . В этом случае последний интеграл называется абсолютно сходящимся.
6. Исследовать, сходится ли интеграл
Решение
При следовательно сходится и данный интеграл.

Слайд 20II. Интеграл от разрывной функции
Пусть
функция f(x) непрерывна при
и имеет точку разрыва при x=b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой.
Если предел, стоящий справа существует, то интеграл называется несобственным сходящимся, иначе расходящимся. Если f(x) имеет разрыв в левом конце отрезка [a,b], то есть при x=a, то по определению
Если f(x) имеет разрыв в некоторой точке , то полагают
, если оба несобственных интеграла, стоящих в правой части равенства существуют.
Пример 1 Вычислить
Решение

Слайд 21Пример 2 Вычислить
Решение Так
как внутри отрезка интегрирования существует точка x=0,
где подынтегральная функция разрывна, то интеграл нужно представить как сумму двух слагаемых:
Вычислим данные интегралы
. Следовательно, на участке [-1;0] интеграл расходится
. Следовательно, на участке [0;1] интеграл расходится. Таким образом, данный интеграл расходится на всем отрезке [-1;1].
Отметим, что, если бы стали вычислять интеграл, не учитывая разрыв подынтегральной функции в точке x=0, то получили бы неверный результат.

Слайд 22Замечание Если f(x), определенная на [a,b], имеет
внутри этого интеграла конечное число точек разрыва
, то интеграл от f(x) на [a,b] определяется следующим образом:
, если каждый интеграл в правой части равенства сходится. Если же, хотя бы один из этих интегралов расходится, то расходится и исходный интеграл.
Имеют место теоремы
Теорема 1 Если на [a,b] функции разрывны в точке b, причем во всех точках [a,b] выполняется неравенство и если сходится, то также сходится.
Теорема 2 Если на [a,b] функции разрывны в точке b, причем во всех точках [a,b] выполняется неравенство и если расходится, то также расходится.
Теорема 3 Если на [a,b] функции знакопеременна и разрывна в точке b и
если сходится, то также сходится. В качестве функций, с
которыми удобно сравнивать функции, стоящие под знаком интеграла, часто берут . Легко проверить, что сходится при и расходится
при
![Замечание Если f(x), определенная на [a,b], имеет внутри этого интеграла конечное число](https://thepresentation.ru/img/tmb/4/345082/73de3640c3037ca236740505b7b4abfe-800x.jpg)
Слайд 23Пример 3 Сходится ли интеграл
Решение Подынтегральная
функция разрывна в точке x=0. Сравнивая ее
с
функцией имеем . Интеграл существует. Следовательно,
интеграл от меньшей функции также существует.

Телом будем
называть любое ограниченное множество
точек пространства.
Тело вращения
– тело, полученное в результате вращения
фигуры вокруг некоторой оси (оси
вращения).
Объем
тела вращения – аддитивная величина,
следовательно, объем тела вращения
можно определить с помощью определенного
интеграла.
Вычисление объема
в прямоугольной системе координат.
Воспользуемся дифференциальным методом.
-
Найти дифференциал
объема
как главную часть приращения объема.
-
Определить пределы
интегрирования.
-
Вычислить объем
.
Дифференциал
объема в прямоугольной системе координат
– объем цилиндра с бесконечно малой
высотой и переменным основанием.
Форма
записи дифференциала объема зависит
от условий задачи – от того, как задана
фигура, которая в результате вращения
образует тело, и что принято за ось
вращения.
О
сь
вращения будем отмечать дугой со стрелкой
2.
y
1
. y
y
O
a x a=0 dx b x
dx
.
.
4.
y
3
.
y
d
d
dy
dy
c
O x c=0 x
.
.
Замечание.
На всех чертежах изображено сечение
тела плоскостью чертежа.
Задача
7.2.1. Фигура, ограниченная линиями
,
вращается вокруг оси
.
Найти объем тела вращения.
▲
– полукубическая
парабола, смещенная на 1 вправо по оси
.
– прямая.
Точки
пересечения полукубической параболы
и прямой:
.
Построение очевидно.
y
B
O 1
2 x
dx
1) Имеем дифференциал
объема:
.
2)
Пределы по чертежу:
.
3)
Вычислим объем:
.
▼
Задача
7.2.2. Фигура, ограниченная линиями
,
вращается вокруг оси
.
Найти объем тела
вращения.
▲
– парабола,
– прямая. Точки пересечения параболы
и прямой:
.
Построим чертеж:
y
A
O 4 x
1) Найдем
.
2)
Пределы определяем из решения системы
при определении точек пересечения
параболы и прямой:
.
3)
Вычисляем объем:
.
▼
Вычисление объема
при параметрическом задании линий,
ограничивающих фигуру.
Задача
7.2.3. Фигура, ограниченная одной
аркой циклоиды
и осью
вращается вокруг оси
.
Найти объем тела вращения.
▲
Чертеж циклоиды
очевиден.
y
O
dx 2πa
x
1)
.
2) Пределы определяются
по пределам
из зависимости
.
Имеем
|
0 |
|
|
|
0 |
|
3)
.
3. Вычисление длин плоских кривых при различных способах задания линий основные понятия и формулы
1.
Длина кривой.
Рассмотрим на плоскости кривую
,
заданную параметрически:
,
где
– непрерывные функции на отрезке
,
причем различным значениям
соответствуют различные точки
(т. е. нет кратных точек). Такую кривую
назовем простой
(плоской)
незамкнутой кривой.
Если точки
совпадают, а остальные точки не являются
кратными, то кривая
называется простой
замкнутой кривой.
Длина
дуги – аддитивная величина, следовательно,
ее можно найти с помощью определенного
интеграла.
Воспользуемся
дифференциальным методом.
-
Найти дифференциал
дуги
в зависимости от способа задания кривой.
-
Определить пределы
интегрирования. -
Вычислить интеграл
от дифференциала дуги.
2. Длина кривой в
декартовых координатах. Если кривая
задана уравнением
,
причем функция
имеет на отрезке
непрерывную производную, то дифференциал
дуги вычисляется по формуле
,
а длина кривой по
формуле
.
Если
кривая задана уравнением
,
причем функция
имеет на отрезке
непрерывную производную, то дифференциал
дуги вычисляется по формуле
,
а длина кривой по
формуле
.
3. Длина кривой,
заданной параметрически. Пусть кривая
задана параметрическими уравнениями
,
причем функции
имеют на отрезке
непрерывные производные. Тогда
дифференциал дуги выражается формулой
а длина кривой
.
4. Длина кривой в
полярных координатах. Если кривая
задана уравнением
,
,
причем функция
имеет на отрезке
непрерывную производную, дифференциал
дуги выражается формулой
,
а длина кривой
.
Замечание.
Задачи на вычисление длин дуг можно
решать без чертежа.
Задача
7.3.1. Найти длину дуги кривой
.
▲
1.
.
2.
Пределы заданы в условии задачи
.
3.
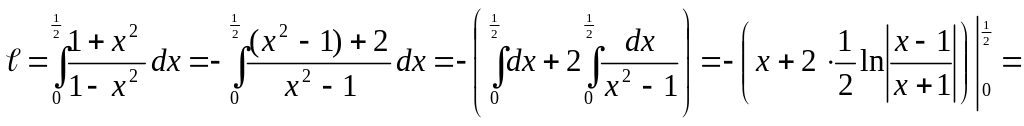
.
▼
Задача
7.3.2. Вычислить длину дуги одной
арки циклоиды
.
▲
Кривая задана
параметрически.
1.
.
2.
Пределы для переменной
определяются по пределам
из уравнения
|
0 |
|
|
|
0 |
|
3.
.
▼
Задача
7.3.3. Вычислить длину логарифмической
спирали
.
▲
Кривая задана
в полярной системе координат.
1.
.
2.
Пределы заданы по условию задачи:
.
3.
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Объемы тел вращения
Краткая теория
Объемы тел, образованных вращением
криволинейной трапеции, ограниченной кривой
, осью
и двумя
вертикалями
и
, вокруг осей
и
, выражаются соответственно формулами:
Объем тела, образованного вращением
около оси
фигуры,
ограниченной кривой
, осью
и двумя
параллелями
и
, можно определять по формуле:
Если кривая задана в иной форме
(параметрически, в полярных координатах и т.д.), то в приведенных формулах
нужно сделать соответствующую замену переменной интегрирования.
В более общем случае объемы тел,
образованных вращением фигуры, ограниченной кривыми
и
(причем
) и прямыми
,
, вокруг координатных осей
и
, соответственно равны:
Объем тела, полученного при вращении
сектора, ограниченного дугой кривой
и двумя
полярными радиусами
,
, вокруг полярной оси, может быть вычислен по формуле:
Этой же формулой удобно пользоваться
при отыскании объема тела, полученного вращением вокруг полярной оси фигуры,
ограниченной некоторой замкнутой кривой, заданной в полярных координатах.
Если
– площадь
сечения тела плоскостью, перпендикулярной к некоторой прямой (которую принимаем
за ось
), в точке с абсциссой
, то объем этого тела равен:
где
и
– абсциссы
крайних сечений тела.
Примеры решения задач
Задача 1
С помощью
определенного интеграла вычислить объем тела, полученного вращением фигуры
вокруг указанной оси координат.
вокруг
оси
Решение
Сделаем
чертеж:
Объем
тела, образованного вращением вокруг оси
фигуры можно найти по формуле:
В нашем
случае получаем
Ответ:
Задача 2
Найдите
объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции,
ограниченной линиями:
и
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Сделаем
чертеж:
Объем
тела можно найти по формуле:
Ответ:
Задача 3
Определить
объем, образованный вращением кривой
вокруг
полярной оси.
Решение
Ответ:
Задача 4
Вычислить
объем тела, ограниченного однополосным гиперболоидом
и
плоскостями
.
Решение
Здесь
удобнее рассмотреть сечения данного тела плоскостями, перпендикулярными к оси
. Тогда объем выразится
формулой:
где
– площадь получаемого сечения, зависящая от
точки с аппликатой
, через которую проходит
секущая плоскость. При пересечении однополосного гиперболоида плоскостью
получается эллипс, который можно определить
уравнениями:
откуда
следует, что полуоси эллипса:
Учитывая, что площадь эллипса с
полуосями
и
равна
, воспользовавшись параметрическим заданием эллипса:
мы можем записать аналитическое
выражение функции
:
Тогда искомый объем:
Ответ:
Приложения определенного интеграла
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Вычисление площади плоской фигуры.
Начать изучение
-
Плоская фигура и ее площадь.
Начать изучение
-
Площадь криволинейной трапеции.
Начать изучение
-
Площадь криволинейного сектора.
Начать изучение
-
Вычисление объема тела.
Начать изучение
-
Тело и его объем.
Начать изучение
-
Цилиндрическое тело и его объем.
Начать изучение
-
Объем тела вращения.
Начать изучение
-
Объем тела с заданными площадями поперечных сечений.
Начать изучение
-
Вычисление длины дуги кривой.
Начать изучение
-
Вычисление площади поверхности вращения.
Начать изучение
-
Применение определенного интеграла при решении физических задач.
Начать изучение
Вычисление площади плоской фигуры.
Плоская фигура и ее площадь.
Произвольное ограниченное множество точек плоскости будем называть плоской фигурой. Если плоскую фигуру можно представить как объединение конечного числа непересекающихся прямоугольников, то такую фигуру назовем клеточной. Подпрямоугольником будем понимать множество точек вида
$$
K = {(x, y): a_{1} leq x leq b_{1}, a_{2} leq y leq b_{2}}nonumber
$$
или множество, получаемое из (K) удалением части границы (или всей границы) множества (K).
Площадью прямоугольника (K) назовем число ((b_{1}-a_{1})(b_{2}-a_{2})) независимо от того, принадлежат или не принадлежат множеству (K) его граничные точки, а площадью клеточной фигуры назовем сумму площадей прямоугольников, из которых составлена эта фигура.
Замечание 1.
Можно показать, что площадь клеточной фигуры не зависит от способа разбиения ее на прямоугольники. Нетрудно также убедиться в том, что площадь клеточной фигуры неотрицательна и обладает свойствами:
- аддитивности, то есть площадь объединения двух непересекающихся клеточных фигур равна сумме их площадей;
- инвариантности, то есть площади двух равных (конгруэнтных) клеточных фигур совпадают;
- монотонности, то есть если клеточные фигуры (G_{1}) и (G_{2}) таковы, что (G_{1} subset G_{2}), то площадь фигуры (G_{1}) не превосходит площади фигуры (G_{2}).
Плоскую фигуру (G) назовем квадрируемой, если для любого (varepsilon > 0) найдутся клеточные фигуры (q) и (Q) такие, что
$$
q subset G subset Q,label{ref1}
$$
$$
0 leq S(Q)-S(q) < varepsilon,label{ref2}
$$
где (S(Q), S(q)) — площади фигур (Q) и (q) соответственно.
Пусть плоская фигура (G) квадрируема. Тогда площадью этой фигуры назовем число (S(G)) такое, что
$$
S(q) leq S(G) leq S(Q)label{ref3}
$$
для любых клеточных фигур (q) и (Q), удовлетворяющих условию eqref{ref1}.
Теорема 1.
Для любой квадрируемой фигуры (G) число (S(G)) существует и единственно, причем
$$
S(G) = sup S(q) = inf S(Q).label{ref4}
$$
Доказательство.
(circ) Так как для любых клеточных фигур (q) и (Q), удовлетворяющих условию eqref{ref1}, выполняется неравенство
$$
S(q) leq S(Q),nonumber
$$
то по теореме об отделимости существуют (sup S(q)) и (inf S(Q)) (супремум и инфимум берутся по всем клеточным фигурам, соответственно содержащимся в фигуре (G) и содержащим эту фигуру), причем
$$
S(q) leq sup S(q) leq inf S(Q) leq S(Q),label{ref5}
$$
откуда
$$
S(q) leq sup S(q) leq S(Q),label{ref6}
$$
Таким образом, число (S(G) = sup S(q)) удовлетворяет условию eqref{ref3}.
Докажем единственность числа (S(G)). Предположим, что наряду с числом (S(G)) существует еще одно число (S'(G)), удовлетворяющее условию eqref{ref3}, то есть
$$
S(q) leq S^{‘}(G) leq S(Q),label{ref7}
$$
Тогда из eqref{ref3} и eqref{ref7} в силу свойств неравенств получаем, что
$$
|S(G)-S'(G)| leq S(Q)-S(q)label{ref8}
$$
для любых клеточных фигур таких, что (q subset G subset Q). Так как (G) -квадрируемая фигура, то разность (S(Q)-S(q)) можно сделать сколь угодно малой в силу условия eqref{ref2}, выбрав соответствующие фигуры (Q) и (q). Поэтому из eqref{ref8} следует, что (S'(G) = S(G)). Таким образом, квадрируемая фигура (G) имеет площадь (S(G)), причем в силу eqref{ref5} справедливо равенство eqref{ref4}. (bullet)
Теорема 2.
Для того чтобы плоская фигура (G) была квадрируема, необходимо и достаточно, чтобы для любого (varepsilon > 0) существовали такие квадрируемые плоские фигуры (tilde{q}) и (tilde{Q}), что
$$
tilde{q} subset G subset tilde{Q},quad 0 leq S(tilde{Q})-S(tilde{q}) < varepsilon,label{ref9}
$$
где (S(tilde{Q})) и (S(tilde{q})) — площади фигур (Q) и (q) соответственно.
Доказательство.
(circ) Необходимость условий eqref{ref9} очевидна, так как по определению квадрируемой фигуры эти условия выполняются, если взять (tilde{q} = q, tilde{Q} = Q), где (q) и (Q) — клеточные фигуры, удовлетворяющие соотношениям eqref{ref1}, eqref{ref2}.
Докажем достаточность. Фиксируя произвольное число (varepsilon > 0), найдем в силу eqref{ref9} такие квадрируемые плоские фигуры (tilde{q}) и (tilde{Q}), что
$$
tilde{q} subset G subset tilde{Q}, 0 leq S(tilde{Q})-S(tilde{q}) < frac{varepsilon}{2},label{ref10}
$$
Так как (tilde{q}) и (tilde{Q}) — квадрируемые плоские фигуры, то существуют клеточные фигуры (Q’) и (q’) такие, что
$$
q’ subset tilde{q},quad tilde{Q} subset Q’,quad 0 leq S(tilde{q})-S(q’) < frac{varepsilon}{4},quad S(Q’)-S(tilde{Q}) < frac{varepsilon}{4}.label{ref11}
$$
Из eqref{ref10} и eqref{ref11} следует, что
$$
q’ subset G subset Q’,quad 0 leq S(Q’)-S(q’) < varepsilon.nonumber
$$
Это означает, что (G) — квадрируемая фигура, причем
$$
S(G) = sup S(tilde{q}) = inf S(tilde{Q}). bulletnonumber
$$
Замечание 2.
Можно доказать, что площадь квадрируемой фигуры обладает свойствами аддитивности, инвариантности и монотонности (см. замечание 1).
Площадь криволинейной трапеции.
Одной из основных задач, приводящих к понятию определенного интеграла, является задача о площади криволинейной трапеции, то есть фигуры (G), задаваемой на плоскости (Oxy) условиями
$$
G = {(x, y): a leq x leq b, 0 leq y leq f(x)},label{ref12}
$$
где (f(x)) — функция, непрерывная на отрезке ([a, b]).
Утверждение 1.
Криволинейная трапеция (G) — квадрируемая фигура, площадь которой (S = S(G)) выражается формулой
$$
S = intlimits_a^b f(x) dx,label{ref13}
$$
Доказательство.
(circ) Пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (M_{i}) и (m_{i}) — соответственно наибольшее и наименьшее значения функции (f) на отрезке (Delta_{i} = [x_{i-1}, x_{i}], Delta x_{i} = x_{i}-x_{i-1}, i = overline{1, n}) (рисунок ниже).
Рассмотрим клеточную фигуру (q), составленную из прямоугольников (q_{i} (i = overline{1, n})), таких, что длина основания (i)-го прямоугольника равна (Delta x_{i}), а высота равна (m_{i}).
Аналогично определяется клеточная фигура (Q), составленная из фигур (Q_{i}), где (Q_{i}) — прямоугольник, длина основания которого (Delta x_{i}), а высота (M_{i}, i = overline{1, n}).
Очевидно, (q subset G subset Q), площади фигур (q) и (Q) соответственно равны
$$
S(q) = sum_{i=1}^{n}m_{i}Delta x_{i},quad S(Q) = sum_{i=1}^{n}M_{i}Delta x_{i}.nonumber
$$
Заметим, что
$$
S(q) = s_{T}, S(Q) = S_{T},label{ref14}
$$
где (s_{T}) и (S_{T}) — соответственно нижняя и верхняя суммы Дарбу для функции (f) при разбиении (T) отрезка ([a, b]).
Так как функция (f(x)) непрерывна на отрезке ([a, b]), то в силу критерия интегрируемости для любого (varepsilon > 0) найдется такое разбиение (T) этого отрезка, что
$$
0 leq S_{T}-s_{T} < varepsilon.nonumber
$$
Иными словами (см. равенства eqref{ref14}), существуют клеточные фигуры (q) и (Q) такие, что
$$
q subset G subset Q,quad 0 leq S(Q)-S(q) < varepsilon,nonumber
$$
то есть выполняются условия eqref{ref1}, eqref{ref2}. Это означает, что (G) — квадрируемая фигура и согласно теореме 1 справедливо равенство eqref{ref4}, которое в силу равенств eqref{ref14} можно записать в виде
$$
S(G) = sup s_{T} = inf S_{T}.label{ref15}
$$
Используя следствие из критерия интегрируемости функции, получаем
$$
sup s_{T} = inf S_{T} = intlimits_a^b f(x) dx.label{ref16}
$$
Из eqref{ref15} и eqref{ref16} следует, что площадь (S = S(G)) криволинейной трапеции (G) выражается формулой eqref{ref13}. (bullet)
Замечание 3.
Ранее площадь (S) фигуры (G) была определена как предел интегральной суммы (sigma_{T} = displaystylesum_{i=1}^{n}f(xi_{i})Delta x_{i}) при (l(T) rightarrow 0) при условии, что этот предел не зависит от разбиения (T) и выборки (xi = {xi_{i}, i = overline{1, n}}), где (xi_{i} in Delta_{i}). Для непрерывной на отрезке ([a, b]) функции (displaystylelim_{l(T) longrightarrow 0}sigma_{T}(xi) = intlimits_a^b f(x) dx), и поэтому оба определения площади приводят к одному и тому же результату.
Рассмотрим теперь фигуру (D) (рис. 37.1), ограниченную отрезками прямых (x = a) и (x = b) и графиками непрерывных на отрезке ([a, b]) функций (y = f_{1}(x)) и (y = f_{2}(x)), где (f_{1}(x) leq f_{2}(x)) при (x in [a, b]). Если (f_{1}(x) geq 0) для всех (x in [a, b]), то площадь фигуры (D) равна разности площадей криволинейных трапеций (D_{2}) и (D_{1}), где (D_{i} = {(x, y): a leq x leq b, 0 leq y leq f_{i}(x)}, i = 1,2). Поэтому площадь фигуры (D) выражается формулой
$$
S(D) = intlimits_a^b (f_{2}(x)-f_{1}(x)) dx.label{ref17}
$$
Формула eqref{ref17} остается в силе и в случае, когда не выполняется условие (f_{1}(x) geq 0) для всех (x in [a, b]). Чтобы убедиться в этом, достаточно сдвинуть фигуру (D) вдоль положительного направления оси (Oy) на (y_{0} = displaystylevertmin_{x in [a, b]}f_{1}(x)vert) и воспользоваться тем, что площади равных фигур совпадают.
Пример 1.
Найти площадь (S) фигуры, ограниченной эллипсом
$$
frac{x^{2}}{a^{2}} + frac{y^{2}}{b^{2}} = 1nonumber
$$
Решение.
(triangle) Искомая площадь (S) равна (4sigma), где (sigma) (рис. 37.2) — площадь криволинейной трапеции, ограниченной осями (Ox), (Oy) и графиком функции (y = b displaystylesqrt{1-frac{x^{2}}{a^{2}}}, 0 leq x leq a). По формуле eqref{ref13} находим
$$
sigma = b intlimits_0^a sqrt{1-frac{x^{2}}{a^{2}}} dx = ab intlimits_0^1 sqrt{1-t^{2}} dt = frac{1}{4} pi abnonumber
$$
(см. пример здесь). Итак, площадь, ограниченная эллипсом с полуосями (a) и (b), равна
$$
S = pi abnonumber
$$
В частности, площадь круга радиуса (R) равна (pi R^{2}). (blacktriangle)
Отсюда следует, что площадь кругового сектора (радиуса (R)), соответствующего центральному углу (alpha), равна
$$
frac{pi R^{2}}{2pi}alpha = frac{R^{2}alpha}{2}.nonumber
$$
Пример 2.
Найти площадь фигуры, ограниченной параболой (y = 6x-x^{2}) и прямой (y = x + 4).
Решение.
(triangle) Парабола (y = 6x-x^{2}) пересекается с прямой (y = x + 4) в точках (A) и В (рис. 37.3), абсциссы которых являются корнями уравнения (6x-x^{2} = x + 4). Решая это уравнение, находим его корни (x_{1} = 1, x_{2} = 4). Согласно формуле eqref{ref17} искомая площадь (S) равна
$$
S = intlimits_1^4 ((6x-x^{2})-(x + 4)) dx = left(frac{5}{2}x^{2}-left.frac{x^{3}}{3}-4xright)right|_{1}^{4} = frac{9}{2}. blacktrianglenonumber
$$
Площадь криволинейного сектора.
Пусть кривая (Gamma) задана в полярной системе координат уравнением
$$
rho = rho(varphi),quad alpha leq varphi leq beta,nonumber
$$
где (rho(varphi)) — неотрицательная и непрерывная на отрезке ([alpha, beta]) функция. Тогда плоскую фигуру (G), ограниченную кривой (Gamma) и, быть может, отрезками двух лучей, составляющих с полярной осью углы (alpha) и (beta) (рис. 37.4), назовем криволинейным сектором.
Утверждение 2.
Криволинейный сектор (G) — квадрируемая фигура, площадь которой (S) выражается формулой
$$
S = frac{1}{2} intlimits_{alpha}^{beta} rho^{2}(varphi) dvarphi.label{ref18}
$$
Доказательство.
(circ) Пусть (T = {varphi_{i}, i = overline{0, n}}) — разбиение отрезка ([alpha, beta]), (m_{i}) и (M_{i}) — соответственно наименьшее и наибольшее значения функции (rho(varphi)) на отрезке (Delta_{i} = [varphi_{i-1}, varphi_{i}], i = overline{1, n}). Обозначим через (q_{i}) и (Q_{i}) круговые секторы, ограниченные лучами (varphi = varphi_{i-1}, varphi = varphi_{i}) и дугами окружностей радиусов (m_{i}) и (M_{i}) соответственно (рис. 37.4). Если (q) — объединение фигур (q_{1}, ldots, q_{n}), а (Q) — объединение фигур (Q_{1}, ldots, Q_{n}), то (q subset G subset Q).Так как (q_{i}) и (Q_{i}) — квадрируемые фигуры, то (q) и (Q) также являются квадрируемыми фигурами, а их площади соответственно равны
$$
S(q) = frac{1}{2} sum_{i=1}^{n}m_{i}^{2}Delta varphi_{i}quad mbox{и}quad S(Q) = frac{1}{2} sum_{i=1}^{n}M_{i}^{2}Delta varphi_{i}.nonumber
$$
Отсюда следует, что (S(q)) и (S(Q)) совпадают соответственно с нижней и верхней суммами Дарбу для функции (displaystylefrac{1}{2} rho^{2}(varphi)) на отрезке ([alpha, beta]). Поэтому (следствие из теоремы о критерии интегрируемости)
$$
sup S(q) = inf S(Q) = frac{1}{2} intlimits_{alpha}^{beta} rho^{2}(varphi) dvarphi.nonumber
$$
Это означает (теорема 2), что (G) — квадрируемая фигура, а ее площадь (S) выражается формулой eqref{ref18}. (bullet)
Пример 3.
Найти площадь фигуры (G), которая ограничена лемнискатой Бернулли (рис. 37.5), заданной уравнением
$$
rho^{2} = a^{2} cos 2varphi.nonumber
$$
Решение.
(triangle) Фигура (G) симметрична относительно координатных осей. Площадь (sigma) той части фигуры (G), которая лежит в первом квадранте, согласно формуле eqref{ref18} равна (sigma = displaystylefrac{1}{2} intlimits_0^{pi/4} a^{2} cos 2varphi dvarphi). Поэтому искомая площадь (S = 4sigma = a^{2}). (blacktriangle)
Вычисление объема тела.
Тело и его объем.
Произвольное ограниченное множество точек пространства будем называть телом.
Основные определения и утверждения, относящиеся к телам, аналогичны соответствующим определениям и утверждениям, рассмотренным выше. Поэтому некоторые утверждения для тел будут опущены.
По аналогии с понятием клеточной фигуры назовем тело клеточным, если его можно представить как объединение конечного числа непересекающихся параллелепипедов, то есть тел вида
$$
M = {(x, y, z): a_{1} leq x leq b_{1}, a_{2} leq y leq b_{2}, a_{3} leq z leq b_{3}},nonumber
$$
а также тел, получаемых из (M) удалением части границы (или всей границы) тела (M). Объемом параллелепипеда (M) назовем число ((b_{1}-a_{1})(b_{2}-a_{2})(b_{3}-a_{3})), а объемом клеточного тела — сумму объемов составляющих его параллелепипедов.
Тело (Omega) будем называть кубируемым, если для любого (varepsilon > 0) найдутся клеточные тела (p) и (P) такие, что
$$
p subset Omega subset P,quad 0 leq V(P)-V(p) < varepsilon,nonumber
$$
где (V(P)) и (V(p)) — объемы тел (P) и (p) соответственно. Как и в случае с площадью фигуры, легко показать, что если тело (Omega) кубируемо, то существует единственное число (V(Omega)) такое, что неравенство
$$
V(p) leq V(Omega) leq V(P)nonumber
$$
выполняется для любых клеточных тел (p), (P), удовлетворяющих условию (p subset Omega subset P); при этом
$$
V(Omega) = sup V(p) = inf V(P).nonumber
$$
Это число (V(Omega)) называют объемом тела (V). Рассмотрим некоторые классы кубируемых (имеющих объем) тел.
Цилиндрическое тело и его объем.
Пусть простой контур (Gamma), расположенный в плоскости (Oxy), ограничивает плоскую фигуру (G). Рассмотрим множество (Omega) точек пространства, которые получаются сдвигом фигуры (G) в направлении положительной полуоси (Oz) на расстояние, не превосходящее (h), где (h) — заданное число, и назовем (Omega) цилиндрическим телом. Граница этого тела состоит из равных (конгруэнтных) фигур (G) и (G_{1}) (рис. 37.6) и части цилиндрической поверхности, образующие которой параллельны оси (Oz). Фигуры (G) и (G_{1}) называют основаниями цилиндрического тела, а расстояние между плоскостями оснований — высотой этого тела.
Утверждение 3.
Если основанием цилиндрического тела (Omega) служит плоская квадрируемая фигура (G), то тело (Omega) кубируемо, а его объем (V(Omega)) равен (S(G)h), где (S(G)) — площадь основания, (h) — высота тела (Omega). В частности, объем прямого кругового цилиндра равен (V = pi R^{2}h), где (R) — радиус основания, (h) — высота цилиндра.
Доказательство.
(circ) По определению плоской квадрируемой фигуры для любого (varepsilon > 0) существуют такие клеточные фигуры (q) и (Q), что
$$
q subset G subset Q,quad 0 leq S(Q)-S(q) < frac{varepsilon}{h},nonumber
$$
Рассмотрим цилиндрические тела (Omega_{1}) и (Omega_{2}) основаниями которых служат соответственно фигуры (q) и (Q), а высота каждого из этих тел равна (h). Тела (Omega_{1}) и (Omega_{2}) являются клеточными, а их объемы соответственно равны
$$
V(Omega_{1}) = S(q)hquad mbox{и}quad V(Omega_{2}) = S(Q)h.nonumber
$$
Так как (Omega_{1} subset Omega subset Omega_{2}, 0 leq V(Omega_{2})-V(Omega_{1}) < varepsilon), то (Omega) — кубируемое тело, а его объем равен (S(G)h). (bullet)
Замечание 4.
Из свойства аддитивности объема и утверждения 3 следует, что ступенчатое тело, то есть тело, являющееся объединением конечного числа цилиндрических тел, кубируемо, если основания цилиндрических тел квадрируемы; при этом объем ступенчатого тела равен сумме объемов тел, из которых составлено ступенчатое тело.
Объем тела вращения.
Утверждение 4.
Тело, образованное вращением вокруг оси (Ox) криволинейной трапеции (G) (условие eqref{ref12}), где (f(x)) — функция, непрерывная на отрезке ([a, b]), кубируемо, а его объем (V) выражается формулой
$$
V = pi intlimits_a^b f^{2}(x) dx.label{ref19}
$$
Доказательство.
(circ) Пусть (T, m_{i}, M_{i}, Delta x_{i}, q, Q) — те же, что и в пункте про «площадь криволинейной трапеции». При вращении вокруг оси (Ox) фигур (q), (G), (Q) получаются тела вращения (p), (Omega), (P) такие, что
$$
p subset Omega subset P,nonumber
$$
причем объемы ступенчатых тел (p) и (P) соответственно равны
$$
V(p) = pi sum_{i=1}^{n}m_{i}^{2}Delta x_{i},quad V(P) = pi sum_{i=1}^{n}M_{i}^{2}Delta x_{i}.nonumber
$$
Так как (V(p)) и (V(P)) равны соответственно нижней и верхней суммам Дарбу для функции (pi f^{2}(x)) при разбиении (T) отрезка ([a, b]), то согласно следствию из теоремы о критерии интегрируемости
$$
sup V(p) = inf V(P) = pi intlimits_a^b f^{2}(x) dx.nonumber
$$
Следовательно, (Q) — кубируемое тело (по теореме, аналогичной теореме 2), а его объем выражается формулой eqref{ref19}. (bullet)
Пример 4.
Найти объем тела, полученного при вращении вокруг оси (Ox) фигуры, ограниченной осью (Ox) и графиком функции (y = sin x, 0 leq x leq pi).
Решение.
(triangle) По формуле eqref{ref19} получаем (V = pi displaystyleintlimits_0^{pi} sin^{2}(x) dx = frac{pi^{2}}{2}). (blacktriangle)
Объем тела с заданными площадями поперечных сечений.
Пусть тело (Omega) заключено между плоскостями, перпендикулярными оси Ох и пересекающими эту ось в точках (x = a) и (x = b), где (a < b) (рис. 37.7).
Обозначим через (G_{x}) фигуру, получаемую в сечении тела (Omega) плоскостью, перпендикулярной оси (Ox) и проходящей через точку (x in [a, b]) этой оси. Будем считать, что при любом (x in [a, b]) фигура (G_{x}) квадрируема, а ее площадь (sigma (x)) — функция, непрерывная на отрезке ([a, b]). Кроме того, предположим, что при проектировании на плоскость, перпендикулярную оси (Ox), фигур (G_{alpha}) и (G_{beta}), где (alpha, beta), — любые точки отрезка ([a, b]), получаются фигуры, одна из которых содержится в другой.
Утверждение 5.
При указанных выше условиях тело (Omega) кубируемо, а его объем (V) выражается формулой
$$
V = intlimits_a^b sigma(x) dx.label{ref20}
$$
Доказательство.
(circ) Пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (m_{i}) и (M_{i})-соответственно наименьшее и наибольшее значения функции (sigma(x)) на отрезке (Delta x_{i} = [x_{i-1}, x_{i}], Delta x_{i} = x_{i}-x_{i-1}, i = overline{1, n}). Так как (sigma(x)) — непрерывная функция, то существуют точки (xi_{i} in Delta_{i}) и (xi_{i}’) такие, что (sigma(xi_{i}) = m_{i}, sigma(xi_{i}’) = M_{i}, i = overline{1, n}).
Обозначим через (Omega_{i}) ту часть тела (Omega), которая заключена между плоскостями (A_{i-1}) и (A_{i}), перпендикулярными оси (Ox) и проходящими соответственно через точки (x_{i-1}) и (x_{i}) (см. рис. 37.7).
Пусть (D_{i}) и (D_{i}’) — цилиндрические тела высотой (Delta x_{i}), построенные на сечениях (G_{xi_{i}}) и (G_{xi_{i}’}) как на основаниях и расположенные между плоскостями (A_{i-1}) и (A_{i}). Тогда (D_{i} subset Omega_{i} subset D_{i}’) а объемы тел (D_{i}) и (D_{i}’) соответственно равны
$$
V(D_{i}) = m_{i}Delta x_{i},quad V(D_{i}’) = M_{i}Delta x_{i}.nonumber
$$
Если (p) — объединение тел (D_{1}, ldots, D_{n}), а (P) — объединение тел (D_{1}’, ldots, D_{n}’), то (p subset Omega subset P),
$$
V(p) = sum_{i=1}^{n}m_{i}Delta x_{i},quad V(P) = sum_{i=1}^{n}M_{i}Delta x_{i}.nonumber
$$
Так как (sup V(p) = inf V(P) = displaystyleintlimits_a^b sigma(x) dx), то (Omega) — кубируемое тело, a его объем выражается формулой eqref{ref20}. (bullet)
Пример 5.
Вычислить объем эллипсоида (displaystylefrac{x^{2}}{a^{2}} + frac{y^{2}}{b^{2}} + frac{z^{2}}{c^{2}} = 1).
Решение.
(triangle) Воспользуемся тем, что площадь фигуры (G), получаемой в сечении эллипсоида плоскостью, параллельной плоскости (Oyz) и отстоящей от нее на расстоянии (x_{0}), где (0 leq x_{0} leq a), равна
$$
S(x_{0}) = pi bc (1-frac{x_{0}^{2}}{a^{2}}).label{ref21}
$$
В самом деле, граница фигуры (G) — эллипс, задаваемый уравнениями
$$
frac{y^{2}}{b^{2}} + frac{z^{2}}{c^{2}} = 1-frac{x_{0}^{2}}{a^{2}},quad x = x_{0}
$$
Полуоси этого эллипса равны (blambda) и (clambda), где (lambda = displaystylesqrt{1-frac{x_{0}^{2}}{a^{2}}}). Используя пример 1, получаем формулу eqref{ref21}, а по формуле eqref{ref20} находим искомый объем эллипсоида:
$$
v = 2 intlimits_0^a S(x) dx = 2pi bc intlimits_0^a left(1-frac{x^{2}}{a^{2}}right) dx = frac{4}{3} pi abc.nonumber
$$
Отсюда следует, что объем шара, радиус которого равен (R), выражается формулой (v = displaystylefrac{4}{3} pi R^{3}) . (blacktriangle)
Вычисление длины дуги кривой.
Утверждение 6.
Если кривая (Gamma), заданная уравнением
$$
Gamma = {boldsymbol{r} = boldsymbol{r}(t), alpha leq t leq beta},label{ref22}
$$
непрерывно дифференцируема, то ее длина (S) выражается формулой
$$
S = intlimits_{alpha}^{beta} |boldsymbol{r}'(t)| dt.label{ref23}
$$
Доказательство.
(circ) Ранее было доказано, что непрерывно дифференцируемая кривая (Gamma) спрямляема (имеет длину), а производная переменной длины дуги (s(t)) этой кривой выражается формулой
$$
s'(t) dt = |boldsymbol{r}'(t)|.label{ref24}
$$
Пусть (S) — длина всей кривой (Gamma); тогда, используя равенство eqref{ref24} и формулу Ньютона-Лейбница, получаем
$$
intlimits_{alpha}^{beta} |boldsymbol{r}'(t)| dt = intlimits_{alpha}^{beta} s'(t) dt = s(beta)-s(alpha) = S.nonumber
$$
так как (s(beta) = S), a (s(alpha) = 0). (bullet)
Если (boldsymbol{r}(t) = (x(t), y(t), z(t))), то формула eqref{ref23} принимает вид
$$
S = intlimits_{alpha}^{beta} sqrt{(x'(t))^{2}+(y'(t))^{2}+(z'(t))^{2}} dt.label{ref25}
$$
а если (Gamma)-плоская кривая, заданная уравнением
$$
y = f(x),quad a leq x leq b,nonumber
$$
то ее длина выражается формулой
$$
S = intlimits_a^b sqrt{1 + (f^{‘}(x))^{2}} dx.label{ref26}
$$
Пример 6.
Найти длину кривой (y = operatorname{ch} x, 0 leq x leq a).
Решение.
(triangle) Применяя формулу eqref{ref26}, находим
$$
S = intlimits_0^a sqrt{1 + operatorname{sh}^{2}x} dx = intlimits_0^a operatorname{ch} x dx = operatorname{sh} a. blacktrianglenonumber
$$
Вычисление площади поверхности вращения.
Пусть (f(x)) — неотрицательная и непрерывная на отрезке ([a, b]) функция, (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (L_{T}) — ломаная с вершинами (A_{i}(x_{i}, f(x_{i})), i = overline{0, n}), соединяющая последовательно точки (A_{0}, A_{1}, ldots A_{n}) (рис. 37.8), (l_{i}) — длина отрезка (mathcal{L}_{i} = [A_{i-1}, A_{i}]) — (i)-го звена ломаной (L_{T}). Тогда
$$
l_{i} = sqrt{(x_{i}-x_{i-1})^{2} + (f(x_{i})-f(x_{i-1}))^{2}}.label{ref27}
$$
При вращении вокруг оси (Ox) звена (mathcal{L}_{i}) образуется боковая поверхность усеченного конуса (цилиндра в случае, когда (f(x_{i}) = f(x_{i-1}))). Площадь этой поверхности, как известно из курса элементарной геометрии, равна
$$
p_{i} = pi (y_{i} + y_{i-1})l_{i},quad y_{k} = f(x_{k}),quad k = overline{1, n},nonumber
$$
откуда следует, что площадь (mathcal{P}_{T}) поверхности, получаемой при вращении ломаной (L_{T}) вокруг оси (Ox), равна
$$
mathcal{P}_{T} = sum_{i=1}^{n}(y_{i} + y_{i-1})l_{i}.label{ref28}
$$
Если существует
$$
lim_{l(T) rightarrow 0} mathcal{P}_{T} = mathcal{P}.label{ref29}
$$
где (l(T)) — мелкость разбиения (T), а (mathcal{P}_{T}) определяется формулой eqref{ref28}, то число (mathcal{P}) называют площадью поверхности вращения, то есть площадью поверхности, образующейся при вращении вокруг оси (Ox) графика функции (y = f(x), a leq x leq b).
Утверждение 7.
Если функция (f) имеет непрерывную производную на отрезке ([a, b]), то предел eqref{ref29} существует, а площадь (mathcal{P}) поверхности вращения выражается формулой
$$
mathcal{P} = 2pi intlimits_a^b f(x) sqrt{1 + (f'(x))^{2}} dx.label{ref30}
$$
Доказательство.
(circ) Из формул eqref{ref28} и eqref{ref27} следует, что
$$
mathcal{P}_{T} = pisum_{i=1}^{n}sqrt{(x_{i}-x_{i-1})^{2} + (y_{i}-y_{i-1})^{2}}(y_{i} + y_{i-1}),label{ref31}
$$
где (y_i=f(x_i)). По теореме Лагранжа
$$
y_{i}-y_{i-1} = f'(xi_{i})Delta x_{i},label{ref32}
$$
где (xi_{i} in Delta_{i} = [x_{i-1}, x_{i}]), (Delta x_{i} = x_{i}-x_{i-1}). Поэтому формулу eqref{ref28} можно записать в виде
$$
mathcal{P}_{T} = pi sum_{i=1}^{n}(y_{i} + y_{i-1}) sqrt{1 + (f'(xi_{i}))^{2}}Delta x_{i}.label{ref33}
$$
Прибавим и вычтем в правой части равенства eqref{ref33} интегральную сумму для интеграла eqref{ref30}, соответствующую разбиению (T) и выборке (xi = xi_{i} (i = overline{1, n})), указанной формулой eqref{ref32}, то есть сумму
$$
sigma_{T} (xi, g)= 2pi sum_{i=1}^{n}(f(xi_{i}))sqrt{1 + (f'(xi_{i}))^{2}}Delta x_{i}.label{ref34}
$$
где (g(x) = 2pi f(x)displaystylesqrt{1 + (f'(x))^{2}}). Заметим, что в силу непрерывности функции (g) для любой выборки (xi) существует
$$
lim_{l(T) rightarrow 0} sigma_{T} (xi, g) = 2pi intlimits_a^b f(x) sqrt{1 + (f'(x))^{2}} dx.nonumber
$$
Поэтому для доказательства формулы eqref{ref30} достаточно показать, что
$$
omega = mathcal{P}_{T}-sigma_{T} (xi, g) rightarrow 0 mbox{при} l(T) rightarrow 0.label{ref35}
$$
Из eqref{ref33} и eqref{ref34} следует, что
$$
omega = pi sum_{i=1}^{n}(y_{i} + y_{i-1}-2f(xi_i)) sqrt{1 + (f'(xi_{i}))^{2}}Delta x_{i}.label{ref36}
$$
При оценке величины (omega) воспользуемся тем, что функция (a) равномерно непрерывна на отрезке ([a, b]), то есть для любого (varepsilon > 0) существует (delta_{varepsilon} > 0) такое, что для любых точек (x’), (x″) из отрезка ([a, b]), удовлетворяющих условию (|x’-x″| < delta_{varepsilon}), выполняется неравенство
$$
|f(x’)-f(x″)| < frac{varepsilon}{C}.label{ref37}
$$
где число (C > 0) будет выбрано ниже.
Пусть разбиение (T) удовлетворяет условию (l(T) = displaystylemax_{1 leq i leq n} Delta x_{i} < delta_{varepsilon}); тогда (|x_{i}-xi_{i}| leq l(T) < delta_{varepsilon}), (|x_{i-1}-xi_{i}| leq l(T) < delta_{varepsilon}), так как (xi_{i} in Delta_{i}). Из eqref{ref37} следует, что
$$
|y_{i}-f(xi_{i})| = |f(x_{i})-f(xi_{i})| < frac{varepsilon}{C},quad |y_{i-1}-f(xi_{i})| < frac{varepsilon}{C},nonumber
$$
и поэтому
$$
|y_{i} + y_{i-1}-2f(xi_{i})| < frac{2varepsilon}{C}.label{ref38}
$$
В силу непрерывности функции (f'(x)) на отрезке ([a, b]) существует число (M > 0) такое, что (0 < displaystylesqrt{1 + (f'(x))^{2}} < M) для всех (x in [a, b]) и, в частности,
$$
0 < sqrt{1 + (f'(xi_{i}))^{2}} < M,quad i = overline{1, n}.label{ref39}
$$
Из eqref{ref36}, eqref{ref38} и eqref{ref39} получаем следующую оценку:
$$
|omega| < pi sum_{i=1}^{n} frac{2varepsilon}{C} M Delta x_{i} = frac{2pi M (b-a)}{C}varepsilon.label{ref40}
$$
Возьмем (C = 2pi M (b-a)) в условии eqref{ref37}; тогда из eqref{ref40} следует, что для любого (varepsilon > 0) существует (delta_{varepsilon} > 0) такое, что для каждого разбиения (T), мелкость (l(T)) которого удовлетворяет условию (l(T) < delta_{varepsilon}), выполняется неравенство (|omega| < varepsilon). Это означает, что (omega rightarrow 0) при (l(T) rightarrow 0). Формула eqref{ref30} доказана. (bullet)
Пример 7.
Пользуясь формулой eqref{ref30}, вычислить площадь (mathcal{P}) поверхности сферического пояса высоты (h), если радиус сферы равен (R).
Решение.
(triangle) Сферический пояс высоты (h) можно получить вращением дуги полуокружности, заданной уравнением (y = f(x) = displaystylesqrt{R^{2}-x^{2}}, a leq x leq b), где ([a, b] subset [-R, R], b-a = h), вокруг оси (Ox) (рис. 37.9). Так как (f'(x) =-displaystylefrac{x}{sqrt{R^{2}-x^{2}}}), то (1 + (f'(x))^{2} = displaystylefrac{R^{2}}{R^{2}-x^{2}}), (f(x)sqrt{1 + (f'(x))^{2}} = R) и по формуле eqref{ref30} получаем (mathcal{P}_{T} = 2pi displaystyleintlimits_a^b R dx = 2pi R(b-a) = 2pi Rh). В частности, площадь поверхности сферы радиуса (R) равна (4pi R^{2}). (blacktriangle)
Применение определенного интеграла при решении физических задач.
Определенный интеграл широко применяется при решении различных физических задач. С помощью определенного интеграла можно вычислять: путь, пройденный материальной точкой, если известна скорость движения; работу переменной силы; силу давления жидкости на плоскую фигуру; статические моменты и координаты центра масс плоской кривой и плоской фигуры и так далее.
Пусть плоская пластинка (G), имеющая форму криволинейной трапеции, определяемой условиями eqref{ref1}, погружена вертикально в жидкость с плотностью (rho) так, что ее боковые стороны параллельны поверхности жидкости и удалены от уровня жидкости на расстояния (a) и (b) (рис. 37.10). Требуется найти силу давления жидкости на пластинку.
Из курса физики известно, что если пластинка погружена в жидкость и расположена горизонтально на расстоянии (h) от поверхности жидкости, то сила давления (mathcal{P}) на одну из сторон пластинки равна
$$
mathcal{P} = g rho hS,nonumber
$$
где (S) — площадь пластинки, (g) — ускорение силы тяжести. Таким образом, сила давления — линейная функция от глубины погружения пластинки. Поэтому естественно разбить пластинку (G) на части прямыми, параллельными поверхности жидкости (оси (Oy)).
Пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]). Прямыми, проведенными через точки (x_{i} (i = overline{1, n-1})), разобьем фигуру (G) на (n) частей (полосок) (G_{i} (i = overline{1, n})). Выделим полоску (G_{i}), ограниченную прямыми (x = x_{i-1}) и (x = x_{i}) (рис. 37.10). Площадь этой полоски приближенно равна площади прямоугольника с основанием (Delta x_{i}) и высотой (f(x_{i})), глубину погружения всех точек полоски (G_{i}) можно считать равной (x_{i}). Поэтому сила давления жидкости на полоску (G_{i}) приближенно равна
$$
g rho x_{i}f(x_{i})Delta x_{i},nonumber
$$
а сумма
$$
mathcal{P}_{T} = sum_{substack{i=1}}^{substack{n}} g rho x_{i}f(x_{i})Delta x_{i}nonumber
$$
приближенно равна силе давления жидкости на пластинку (G).
Если (l(T) rightarrow 0), где (l(T)) — мелкость разбиения (T), а функция (f) непрерывна на отрезке ([a, b]), то (mathcal{P}_{T} rightarrow mathcal{P}), где
$$
mathcal{P} = g intlimits_a^b rho x f(x) dx.label{ref41}
$$
Число (mathcal{P}) выражаемое формулой eqref{ref41}, называют силой давления жидкости на пластинку (G).
Пример 8.
Вычислить силу давления (mathcal{P}) жидкости с плотностью (rho) на вертикальную стенку, имеющую форму полукруга радиуса (R) и погруженную в жидкость так, что диаметр полукруга расположен на поверхности жидкости (рис. 37.11).
Решение.
(triangle) Выберем систему координат так, как указано на рис. 37.11. Пользуясь формулой eqref{ref41}, где (f(x) = sqrt{R^{2}-x^{2}}, a = 0, b = R), получаем
$$
mathcal{P} = 2g rho intlimits_0^R x sqrt{R^{2}-x^{2}} dx =-left.frac{2}{3} g rho (R^{2}-x^{2})^{3/2}right|_{0}^{R} = frac{2rho g}{3} R^{3}. blacktrianglenonumber
$$