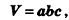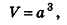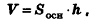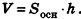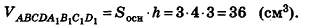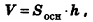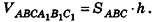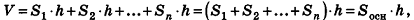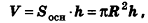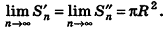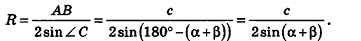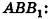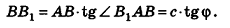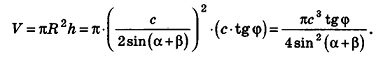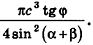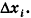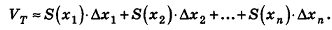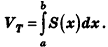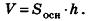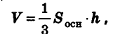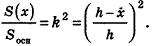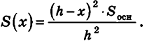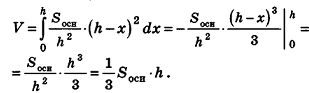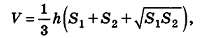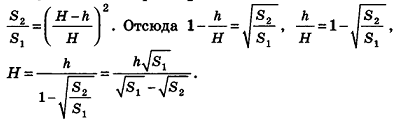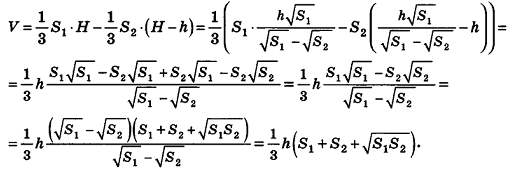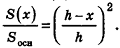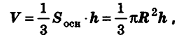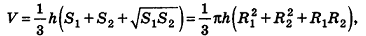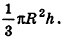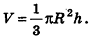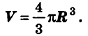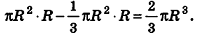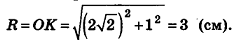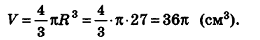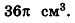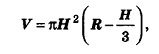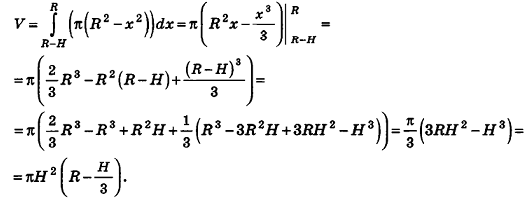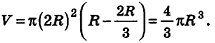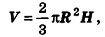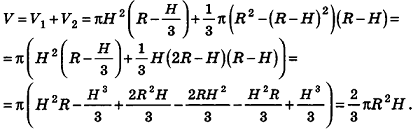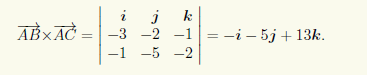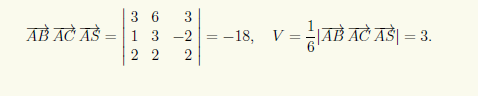Формулы объема геометрических фигур
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
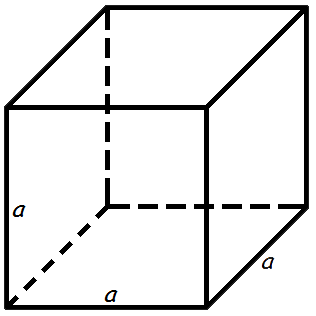
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.
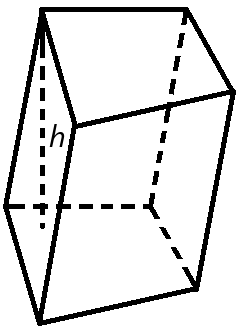
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
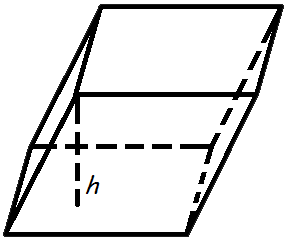
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
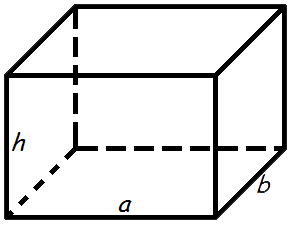
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
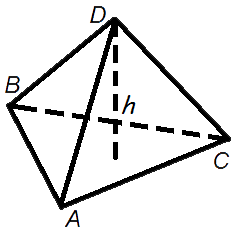
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
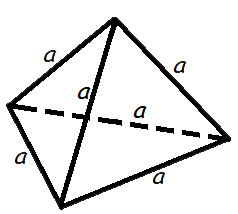
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
V = π R2 h
V = So h
где V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592.
Измерение объёма тела по формуле — возможные способы, единицы измерения
Содержание:
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Понятие объема тела
Объем является количественным параметром пространства, занятого телом или веществом.
Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:
- форма;
- линейные размеры.
Главным свойством объема принято считать аддитивность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.
Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.
Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.
Свойства объема тела
В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:
- Объем тела не может быть отрицательной величиной.
- В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
- Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
- Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
- В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: (V1<V2
).
Как вычислить объем тела: все формулы
Существует практический способ определения объема тела, включая тела, обладающие сложной формой и геометрией. Данная методика основана на законе Архимеда и предполагает погружение рассматриваемого тела в некую жидкость. По результатам следует измерить объем вытесненной телом жидкости. Данная величина равна объему измеряемого тела.
Формула расчета объема тела, исходя из известных величин массы и плотности:
(V={frac {m}{rho }})
Здесь m определяется, как масса, а rho является средней плотностью тела.
В том случае, когда тела обладают простыми геометрическими формами, в решении задач допустимо использовать специальные формулы. К примеру, для того чтобы найти объем куба, ребро которого равно а, следует применить такую формулу: (V=a^{3}).
Вычислить объем некого прямоугольного параллелепипеда можно путем умножения длины, ширины и высоты. Запишем другие распространенные формулы для расчета объемов геометрических фигур:
- куб, формула объема: (V=a^{3}):
- прямоугольный параллелепипед, формула объема: (V=abc) (произведение длин трех сторон):
- призма, формула объема: ( V=Bh) (произведение площади основания и высоты):
- пирамида, формула объема: (V={frac {1}{3}}Bh:)
- параллелепипед, формула объема: (V=abc{sqrt {K}}, {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}:
) -
- тетраэдр, формула объема: (V={{sqrt {2}} over 12}a^{3}:)
- шар, формула объема: (V={frac {4}{3}}pi r^{3}):
- эллипсоид, формула объема: (V={frac {4}{3}}pi abc):
- прямой круговой цилиндр, формула объема: (V=pi r^{2}h):
- конус, формула объема: (V={frac {1}{3}}pi r^{2}h):
- тело вращения, формула объема: (V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x):
В том случае, когда необходимо определить объем, которым обладает некое тело, имеющее сложную форму, нужно разбить мысленно данное тело на отдельные части. Такие части целого должны иметь простую форму. Далее следует сложить вычисленные объемы простых тел. Результат будет являться значением объема начального тела.
Примеры решения задач
Задача 1
Задача
Имеется пара шаров. Радиус первого шара в 5 раз превышает радиус второго шара.
Требуется определить, во сколько раз площадь поверхности второго шара меньше по сравнению с площадью поверхности первого шара
Решение
Рассчитать площадь поверхности можно по формуле:
(S=4pi R^2)
Тогда запишем отношения площадей пары шаров:
(dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2})
Сравним радиусы геометрических фигур:
(R_1=5R_2)
В результате:
(dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их (K_1) и (K_2).
Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.
Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).
Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
(S=pi R (R+l))
Запишем отношения площадей полной поверхности заданных конусов:
(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})
Согласно условию задачи, имеем:
(R_1=4l_1, R_2=frac12R_1=2l_1)
В результате:
(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)
Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})
Известно, что:
(a_1=7a_2, b_2=2b_1, c_1=3c_2)
В результате:
(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)
Ответ: 10.
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Решение
Составим формулу для расчета площади боковой поверхности конуса:
(S=pi Rl)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)
Ответ: 0,2.
Задача 5
Имеется пара шаров. Объем первой фигуры составляет 54. Радиус второй фигуры в 3 раза меньше по сравнению с радиусом первой. Нужно определить объем второго шара.
Решение
Запишем формулу, согласно которой можно определить объем шара:
(V=dfrac43 pi R^3)
Составим отношение объемов двух фигур:
(dfrac{54}{V_2}=dfrac{V_1}{V_2}= dfrac{frac43 pi ,R_1^3}{frac43 pi ,R_2^3}=left(dfrac{R_1}{R_2}right)^3)
По условиям задачи:
(R_1=3R_2)
В результате:
(dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad V_2=dfrac{54}{27}=2)
Ответ: 2.
Задача 6
Имеется некая емкость конусообразной формы. Ее заполнили до половины с помощью 75 гр жидкости. Необходимо вычислить вес жидкости, которую нужно добавить в емкость, чтобы заполнить ее до верхнего края.
Решение
Вспомним формулу объема из курса физики:
(V=frac{m}{rho})
Предположим, что O является центром основания большего конуса. Пусть Q — центр основания меньшего конуса, а S обозначает общую вершину данных фигур. В одной плоскости построим радиусы OA и QB:
В таком случае:
(QBparallel OA)
(triangle SQBsim triangle SOA)
В результате:
(dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21)
Получим, что:
(m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho= dfrac13cdot picdot QScdot QB^2 cdot rho)
Можно сделать вывод, что:
(m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho= dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
Таким образом, потребуется долить в емкость:
(600-75=525 {small{text{грамм}}})
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.
Исследуем плоскость ASO. Построим (A’Hparallel SO), где SO представляет собой высоту начальной фигуры. В таком случае:
(A’Hperp ABC)
В результате получилось расстояние, которое равно (frac13SO:)
(triangle AA’Hsim triangle ASO)
(dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad SA=3AA’ quadRightarrowquad SA’=dfrac23SA)
Таким образом:
(SQ=frac23SO)
(triangle ASBsim triangle A’SB’)
Получим, что:
(dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad A’B’=dfrac23AB)
Запишем отношения объемов пирамид:
(dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}= dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot AB^2}=dfrac{SQ}{SO}cdot left(dfrac{A’B’}{AB}right)^2=dfrac23cdot left(dfrac23right)^2=dfrac8{27})
В результате объем малой фигуры составит:
(V_{{small{text{м}}}}=dfrac8{27}cdot 54=16)
Ответ: 16.
Задания для самостоятельной работы
Задание 1
Имеется пара конусов. Вторая фигура обладает радиусом, который в три раза больше по сравнению с радиусом первой фигуры. Второй конус выше первого в шесть раз. Объем второй фигуры равен 18. Требуется вычислить, чему равен объем первого конуса.
Решение
Формула определения объема конуса:
(V=frac13pi R^2h)
Запишем отношения объемов двух фигур:
(dfrac{V_1}{18}=dfrac{V_1}{V_2}= dfrac{frac13pi ,R_1^2,h_1}{frac13 pi ,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot dfrac{h_1}{h_2})
Исходя из условий задачи:
(R_2=3R_1)
(h_1=6h_2)
В результате:
(dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}= dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot 18=12)
Ответ: 12
Задание 2
Дано два шара. Объем первого шара в 343 раза больше по сравнению с объемом второго шара. Нужно вычислить, во сколько раз радиус первой фигуры больше, чем радиус второй фигуры.
Решение
Запишем формулу для нахождения объема шара:
(V=dfrac43 pi R^3)
Составим отношения объемов данных шаров:
(dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}= left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
(S=2pi RH)
Составим отношение площадей боковых поверхностей двух фигур:
(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})
В результате:
(R_2=4R_1, H_1=5H_2)
Таким образом:
(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)
Получим, что:
(S_2=dfrac{16cdot 4}5=12,8)
Ответ: 12,8.
Задание 4
Имеется некая емкость конусообразной формы. Объем этой емкости составляет 2700 мл. Требуется рассчитать количество жидкости, налитой в емкость, если ее уровень в 3 раза меньше по сравнению с высотой емкости.
Решение
Введем обозначения, как на рисунке:
В таком случае:
(QBparallel OA и triangle SQBsim triangle SOA)
Таким образом:
(dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13)
Соотношение объемов жидкости до определенной линии и емкости:
(dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}= dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27})
В результате:
(V_{small{text{ж}}}=dfrac1{27}V=100)
Ответ: 100.
Задача 5
На рисунке изображены фигуры в виде шаров. Первый шар имеет радиус 6. Второй шар имеет радиус 2. Нужно вычислить, во сколько раз объем первой фигуры превышает объем второй фигуры.
Решение
Запишем формулу для расчета объема шара, который не может изменяться:
(V=dfrac43 pi R^3)
Составим отношение объемов двух шаров:
(dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}= left(dfrac62right)^3=27)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.
Содержание:
Объёмы поверхностей геометрических тел:
То, чем в предыдущие эпохи занимались только зрелые умы ученых мужей, в более позднее время стало доступным для понимания юношей.
С древних времен люди применяли геометрию для решения конкретных житейских проблем — нахождения объемов сосудов, строений и кораблей, количества краски, необходимой для ремонта помещения. На основании практического опыта были разработаны методы вычисления объемов тел и площадей поверхностей. Но нахождение соответствующих формул, а тем более их доказательств заняло немало страниц в истории геометрической науки. Многие выдающиеся ученые внесли свой вклад в развитие теории объемов, а популяризаторы математики — в упрощение и доступное изложение этой теории.
Основной целью данной главы является формирование представлений об объемах и площадях поверхностей, обоснование соответствующих формул для основных пространственных фигур. Вы. научитесь использовать различные методы нахождения объемов, как строго геометрические, так и те, которые объединяют в себе геометрию и начала анализа. При изучений объемов тел полезно будет вспомнить и систематизировать материал о площадях фигур на плоскости. Подходы, которые применялись для получения основных формул площадей, будут надежным фундаментом для построения теории объемов.
В данной главе речь пойдет о всех основных фигурах, которые вы изучали в течение года, в частности о тесной связи многогранников и тел вращения. Это даст вам возможность, с одной стороны, вспомнить основные факты из курса геометрии, а с другой — на основании формул для площадей поверхностей многогранников получить соответствующие результаты для тел вращения.
Задачи данной главы содержат много геометрических конфигураций, что позволит вам переосмыслить весь курс стереометрии с точки зрения применения своих знаний на практике, в частности для нахождения, пожалуй, самых распространенных в жизни геометрических величин — объемов и площадей поверхностей. Ради этого бесценного опыта вы и изучали, в конце концов, геометрию в пространстве.
Объемы
Понятие объема хорошо известно на уровне повседневного опыта: мы покупаем пакет сока определенного объема, рассчитываем, какой объем займет в квартире новая мебель, берем для приготовления блюда кастрюлю соответствующего объема. Придадим этим наглядным представлениям об объеме тела определенную математическую строгость.
Понятие объема многогранников
Для дальнейших рассуждений полезно объединить практический опыт и известную уже теорию площадей многоугольников. По аналогии с ней мы и будем строить теорию объемов пространственных тел, в первую очередь многогранников.
Объем характеризует величину части пространства, которую занимает геометрическое тело, и измеряется, как и площадь, в определенных единицах. Единицей измерения площадей является площадь единичного квадрата, а за единицу измерения объема принимается объем единичного куба, то есть куба, ребро которого равно единице длины. Например, если за единицу измерения длины принимается 1 мм, 1 см, 1 дм или 1 м, то за единицу измерения объема принимается объем куба с ребром 1 мм, 1 см, 1 дм или 1 м. Соответствующая единица объема называется кубическим миллиметром (1 мм3), кубическим сантиметром (1 см3), кубическим дециметром или литром (1 дм3 или 1 л), кубическим метром (1 м3). Таким образом, вычисление объемов тел разной формы основано на сравнении с объемом единичного куба.
Измерить объем тела на практике можно, например, погрузив его в воду и подсчитав количество вытесненной телом воды. Но во многих случаях это не целесообразно, поэтому очень полезно вывести и научиться применять формулы для вычисления объемов. Соответствующая теория основана на аксиомах объема многогранников.
- Равные многогранники имеют равные объемы.
- Бели многогранник составлен из нескольких многогранников, то его объем равен сумме объемов этих многогранников.
- Объем куба с ребром, равным единице длины, равен единице объема.
Итак, объем многогранника — это положительная величина, Числовое значение которой удовлетворяет аксиомам объема. : — Как правило, объем обозначают буквой V.
Приведенные аксиомы имеют и практическую основу. Действительно, все пакеты, имеющие форму прямоугольного параллелепипеда и одинаковые размеры, содержат одинаковое количество сока.
Тела, имеющие равные объемы, называются равновеликими.
Если же каждый из двух пакетов можно разлить в одинаковое количество маленьких пакетиков, то сумма объемов этих пакетиков будет равна объему каждого из них, то есть данные пакеты имеют одинаковый объем.
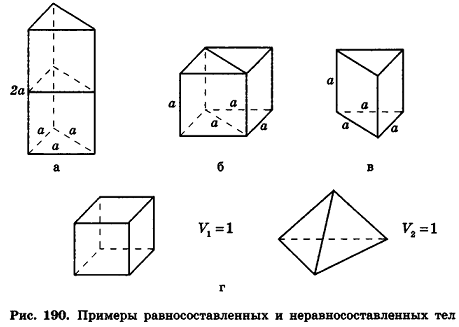
Тела, составленные из одних и тех же многогранников, называются равносоставленными. Например, равносоставленными будут тела, изображенные на рисунке 190, а, б: прямая треугольная призма и прямой параллелепипед. Действительно, каждая из этих фигур составлена из двух одинаковых прямых призм, таких как на рисунке 190, в.
Очевидно, что объемы равносоставленных многогранников равны по второй аксиоме. Интересно, что обратное утверждение неверно (в отличие от аналогичной теоремы для площадей). Так, многогранники равного объема не всегда можно разбить на конечное число равных многогранников. В частности, куб и правильный тетраэдр равных объемов (рис. 190) не являются равносоставленными.
Объем параллелепипеда
Простейшей фигурой с точки зрения вычисления объема является прямоугольный параллелепипед.
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 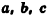
Приведем рассуждения, на которых основано доказательство данной теоремы.
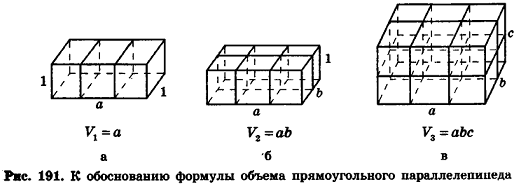
Сначала рассмотрим прямоугольный параллелепипед с измерениями а, 1, 1. Так как в отрезке а единица измерения длины помещается а раз, то единичный куб помещается в параллелепипед также а раз. Значит, объем прямоугольного параллелепипеда равен а (рис. 191, а).
Аналогично объем прямоугольного параллелепипеда с измерениями 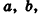
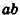
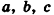
Полное доказательство данной теоремы приведено в Приложении 2.
Следствие (формула объема куба)
Объем куба равен кубу его ребра:
где а — ребро куба.
Нам известно, что площадь прямоугольника равна произведению двух его измерений, а параллелограмма — произведению его стороны на проведенную к ней высоту. По аналогии нетрудно предположить, что объем произвольного параллелепипеда также можно найти через площадь основания и соответствующую высоту.
Теорема (формула объема параллелепипеда)
Объем параллелепипеда равен произведению площади его основания на высоту:
где 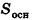
Доказательство:
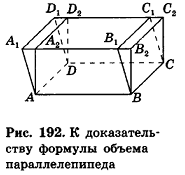
Очевидно, что для прямоугольного параллелепипеда данная формула верна. Докажем ее для наклонного параллелепипеда 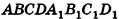
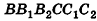
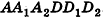
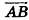
При описанном преобразовании параллелепипеда площадь его основания и высота сохраняются, а две боковые грани становятся перпендикулярными плоскости основания ABC. Если выполнить аналогичное преобразование с помощью плоскостей, проходящих через АВ и DC перпендикулярно основанию ABCD, получим прямой параллелепипед с основанием ABCD, равновеликий исходному. При этом высоты параллелепипедов также сохраняются.
Теперь проведем через точки А я В плоскости, перпендикулярные АВ (рис. 193). Дополняя прямой параллелепипед одной треугольной призмой (I) и отсекая равную ей другую призму (2), получим прямоугольный параллелепипед, равновеликий предыдущему.
Объем полученного прямоугольного параллелепипеда равен 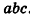
основания и высота сохраняются, то и объем исходного параллелепипеда можно вычислить с помощью полученной формулы. Итак, объем наклонного параллелепипеда
Таким образом, объем произвольного параллелепипеда вычисляется по формуле
Теорема доказана.
Пример №1
В основании наклонного параллелепипеда лежит прямоугольник со сторонами 3 см и 4 см. Боковое ребро параллелепипеда равно 6 см. Найдите объем данного параллелепипеда, если две его боковые грани перпендикулярны плоскости основания, а две другие наклонены к ней под углом 30°.
Решение:
Пусть дан параллелепипед 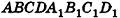
Пусть грани 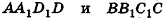
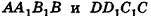
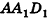
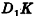
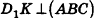
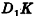
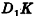
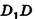
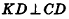
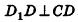
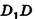
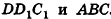
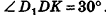
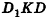
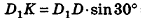
Таким образом,
Ответ: 36 см3.
Объем призмы
На плоскости для получения формулы площади треугольника было удобно дополнить треугольник до параллелограмма. Далее, для получения формулы площадей других многоугольников, целесообразно было разбить их на треугольники. Применим аналогичные приемы для вывода формулы объема призмы.
Теорема (формула объема призмы)
Объем призмы равен произведению площади ее основания на высоту:
где 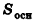
Доказательство:
Пусть дана треугольная призма 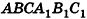
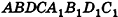
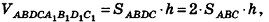
Применим только что выведенную формулу объема треугольной призмы к рассмотрению произвольной призмы.
Разобьем основание призмы на треугольники, а призму — на соответствующие треугольные призмы с высотой h (рис. 196).
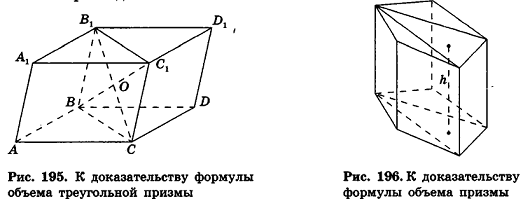
По аксиоме, объем данной призмы равен сумме объемов составляющих ее треугольных призм:
где 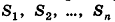
Теорема доказана.
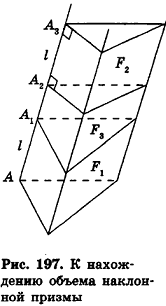
Пример №2
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения: 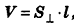
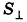
Решение:
Рассмотрим наклонную призму F1 с ребром АА1 = I (рис. 197). Проведем два ее перпендикулярных сечения, расстояние между плоскостями которых I и которые не имеют с данной призмой общих точек. При этом получим прямую призму F2 и многогранник F3 (рис. 197). Многогранник, гранник, как совмещаются параллельным переносом на вектор 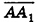
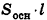
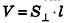
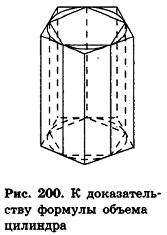
Объем цилиндра
При обосновании формулы площади круга в планиметрии мы использовали вписанные в окружности и описанные около них многоугольники. Применим аналогичные рассуждения и в пространстве, заменив круг на цилиндр, а многоугольники — на призмы. Дадим соответствующие определения.
Определение:
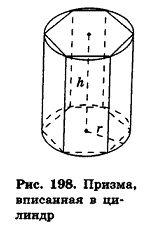
Прямая призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра.
При этом цилиндр называется описанным около призмы. Очевидно, что боковые ребра призмы — образующие цилиндра, а высоты прямой призмы и описанного около нее цилиндра равны (рис. 198).
Определение:
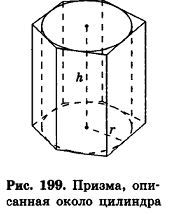
Прямая призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра.
При этом цилиндр называется вписанным в призму (рис. 199). Очевидно, что высоты прямой призмы и вписанного в нее цилиндра равны.
Теорема (формула объема цилиндра)
Объем цилиндра равен произведению площади его основания на высоту:
где 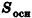
Доказательство:
Впишем в данный цилиндр радиуса R и высоты h правильную п-угольную призму с площадью основания S’n и опишем около него правильную n-угольную призму с площадью основания 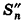
Отсюда следует, что при неограниченном возрастании п объемы вписанных призм 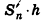
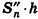
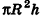
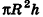
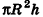
Теорема доказана.
Пример №3
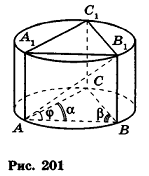
Основание прямой призмы — треугольник со стороной с-и прилежащими к ней углами 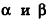
Решение:
Пусть дана прямая треугольная призма 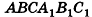
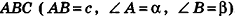
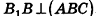
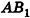
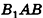
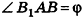
Рассмотрим цилиндр, описанный около данной призмы. Его основания описаны около оснований призмы, высота равна высоте призмы.
По теореме синусов для треугольника ABC имеем:
Из прямоугольного треугольника
Следовательно, объем цилиндра равен:
Ответ:
Объемы пирамиды, конуса и шара
Рассмотрим способ вычисления объемов тел, в основе которого лежит понятие интеграла, известное из курса алгебры и начал анализа.
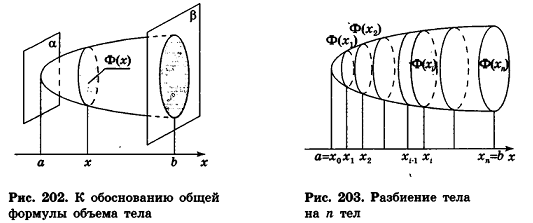
Общая формула объема
Пусть тело Т, объем которого требуется вычислить, расположено между двумя параллельными плоскостями 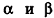
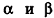
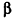
Будем рассматривать случай, когда любое сечение тела Ф(х) плоскостью, перпендикулярной-оси Ох и пересекающей эту ось в точке (х;0;0), является кругом или многоугольником (такой случай возможен, если Ф(х) — точка).
Обозначим площадь фигуры Ф(х) через S(x). Допустим, что S(x) — непрерывная функция при 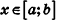
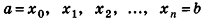
Эти плоскости разобьют тело Т на n тел: 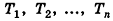
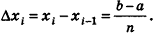
Учитывая, что объем цилиндра и призмы равен произведению площади основания на высоту, то есть 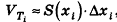
При неограниченном возрастании n правая часть данной формулы приближается сколь угодно близко к объему тела Т. С другой стороны, так как S(x) непрерывна на 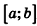
Таким образом, мы получили формулу для вычисления объема тела с помощью интеграла. Будем называть ее интегральной формулой объема.
Из этой формулы вытекает интересное и удобное в применении следствие, формулировка которого принадлежит итальянскому математику Бонавентуре Кавальери.
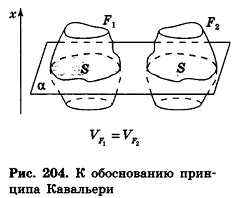
Принцип Кавальери
Если при пересечении двух тел F1 и F2 плоскостями, параллельными одной и той же плоскости а, в сечениях получаются фигуры с равными площадями, то объемы данных тел равны.
Это утверждение легко вывести из интегральной формулы объема, если расположить систему координат так, чтобы ось Ох была перпендикулярна плоскости а (рис. 204). Применение интеграла и принципа Кавальери позволяет значительно упростить нахождение формул, выражающих объемы многих важных тел.
Объем пирамиды и конуса
В пунктах 15.3 и 15.4 мы установили, что объемы призмы и цилиндра определяются одной и той же формулой:
Поэтому вполне естественно предположить, что будут совпадать формулы для объемов пирамиды и конуса.
Теорема (формула объема пирамиды)
Объем пирамиды равен трети произведения площади основания на высоту:
где 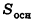
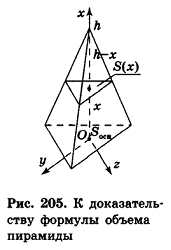
Доказательство:
Разместим пирамиду в системе координат так, чтобы ось Ох была направлена вдоль высоты, а основание’ принадлежало бы плоскости 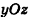
Отсюда
Применяя теперь для пирамиды интегральную формулу объема, получим:
Теорема доказана.
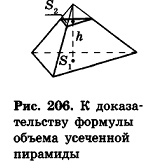
Следствие (формула объема усеченной пирамиды)
Объем усеченной пирамиды вычисляется по формуле:
где h — высота усеченной пирамиды, 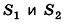
Доказательство:
Дополним данную усеченную пирамиду до полной с высотой Н (рис. 206). Тогда высота дополняющей пирамиды будет равна H-h. Из подобия полной и дополняющей пирамид, площади оснований которых равны 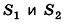
По аксиомам объема, объем усеченной пирамиды равен разности объемов полной и дополняющей пирамид. Следовательно,
Формула доказана.
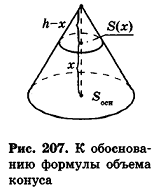
Заметим, что при доказательстве теоремы об объеме пирамиды и ее следствия, кроме интегральной формулы объема, мы применили только тот факт, что плоскость, параллельная основанию, отсекает пирамиду, для площади основания S(x) и высоты h-x которой верна формула
Но эта формула, по доказанному в п. 13.2, также верна и для конуса (рис. 207). Поэтому аналогичными формулам объема и их доказательствам для пирамиды и усеченной пирамиды будут формулы объема и их доказательства для конуса и усеченного конуса.
Теорема (формула объема конуса)
Объем конуса равен трети произведения площади основания на высоту:
где 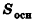
Следствие (формула объема усеченного конуса)
Объем усеченного конуса вычисляется по формуле
где h — высота усеченного конуса, 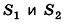
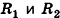
С помощью вписанных и описанных призм мы вывели формулу для объема цилиндра. Подобную связь можно установить также для конусов и пирамид.
Определение:
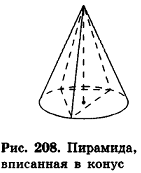
Пирамида называется вписанной в конус, если их вершины совпадают, а основание пирамиды вписано в основание конуса.
При этом конус называется описанным около пирамиды.
Очевидно, что высоты пирамиды и описанного конуса равны, а боковые ребра пирамиды являются образующими конуса (рис. 208).
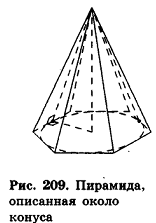
Определение:
Пирамида называется описанной около конуса, если их вершины совпадают, а основание пирамиды описано около основания конуса.
При этом конус называется вписанным в пирамиду.
Очевидно, что высоты пирамиды и вписанного конуса равны, а высоты боковых граней пирамиды являются образующими конуса (рис. 209).
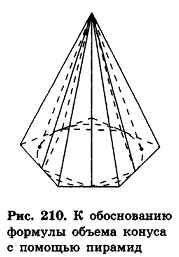
Рассмотрим правильные л-угольные пирамиды, вписанные в данный конус, и правильные л-угольные пирамиды, описанные около него (рис. 210).
Если число n сторон оснований этих пирамид неограниченно возрастает, то площади их оснований стремятся к площади круга, лежащего в основании конуса. Следовательно, их объемы стремятся 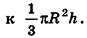
Из этих рассуждений становится понятным другое обоснование формулы объема конуса
Объем шара и его частей
Непосредственно получить только из геометрических рассуждений формулу для объема шара очень сложно. Но с помощью интегральной формулы объема и принципа Кавальери доказательство соответствующих результатов является простым и наглядным.
Теорема (формула объема шара)
Объем шара радиуса R вычисляется по формуле
Доказательство:
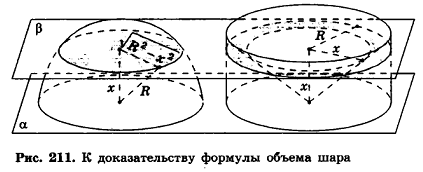
Найдем сначала объем полушара, применив принцип Кавальери.
Пусть дан полушар Fl радиуса R. На плоскость а, содержащую основание полушара, поставим цилиндр, радиус и высота которого также равны R. В цилиндр впишем конус, вершина которого совпадает с центром основания цилиндра в плоскости а, а основание — с другим основанием цилиндра (рис. 211).
Сравним объем V1 полушара с объемом V2 тела F2, ограниченного нижним основанием цилиндра и боковыми поверхностями цилиндра и конуса.
Проведем плоскость 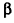
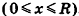
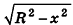
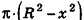
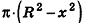
Объем шара вдвое больше объема полушара, следовательно, вычисляется по формуле 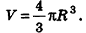
Пример №4
Сечение шара, удаленное от его центра на 1 см, имеет площадь 8л см2. Найдите объем шара.
Решение:
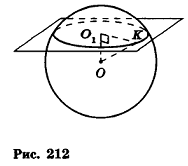
Пусть дан шар с центром О. Сечение шара некоторой плоскостью а является кругом с центром 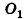
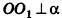
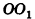
Пусть точка К сферы, ограничивающей шар, принадлежит данному сечению (рис. 212). Тогда площадь сечения равна 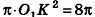
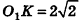
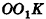
По формуле объема шара
Ответ:
Найдем теперь объемы частей шара.
Определение:
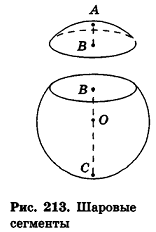
Шаровым сегментом называется часть шара, отсекаемая от него некоторой плоскостью.
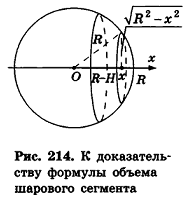
На рисунке 213 плоскость сечения, проходящая через точку В, разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется основанием этих сегментов, а длины отрезков диаметра, перпендикулярного плоскости сечения,— высотами сегментов. Так, на рисунке 213 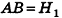
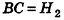
Теорема (формула объема шарового сегмента)
Объем шарового сегмента вычисляется по формуле
где R — радиус шара, Н — высота сегмента.
Доказательство:
Применим для шарового сегмента интегральную формулу объема.
Введем декартову систему координат так, чтобы ее начало совпадало с центром шара.
Тогда часть шара, ограниченная плоскостями 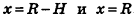
Радиус сечения шарового сегмента плоскостью, пересекающей ось Ох в точке (х;0;0), равен 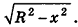
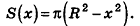
Теорема доказана.
Заметим, что при Н -2R из только что доказанной формулы следует еще один способ нахождения формулы объема шара:
Определение:
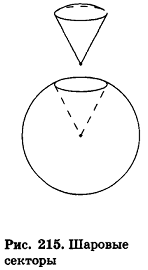
Шаровым сектором называется тело, ограниченное сферической поверхностью шарового сегмента и боковой поверхностью конуса, основанием которого является основание сегмента, а вершиной — центр шара.
Очевидно, что если шаровой сегмент меньше полушара, его дополняют конусом для получения шарового сектора; если же шаровой сегмент больше полушара, то для получения шарового сектора конус из него удаляют (рис. 215).
Теорема (формула объема шарового сектора)
Объем шарового сектора вычисляется по формуле
где R — радиус шара, Я — высота соответствующего шарового сегмента.
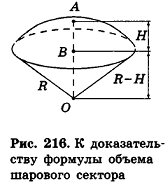
Доказательство:
Рассмотрим случай шарового сектора, высота Я соответствующего шарового сегмента для которого меньше R (рис. 216).
Тогда его объем равен сумме объема сегмента 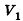
Случай, когда высота Н больше или равна R, рассмотрите самостоятельно.
Теорема доказана.
Определение:
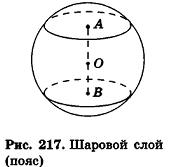
Шаровым слоем (поясом) называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Расстояние между этими плоскостями называется высотой шарового слоя, а сечения, ограничивающие слой,— основаниями шарового слоя (рис. 217).
Заметим, что объем шарового слоя можно вычислить двумя способами:
- как разность объемов двух шаровых сегментов;
- как разность объема шара и объемов двух сегментов, не входящих в слой.
Объемы подобных тел
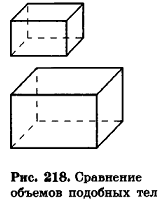
Из повседневного опыта нам хорошо известно, что при увеличении размеров предмета его объем также увеличивается. Например, легко сравнить объемы двух аквариумов, размеры одного из которых вдвое меньше соответствующих размеров другого (рис. 218): объемы отличаются в 8 раз.
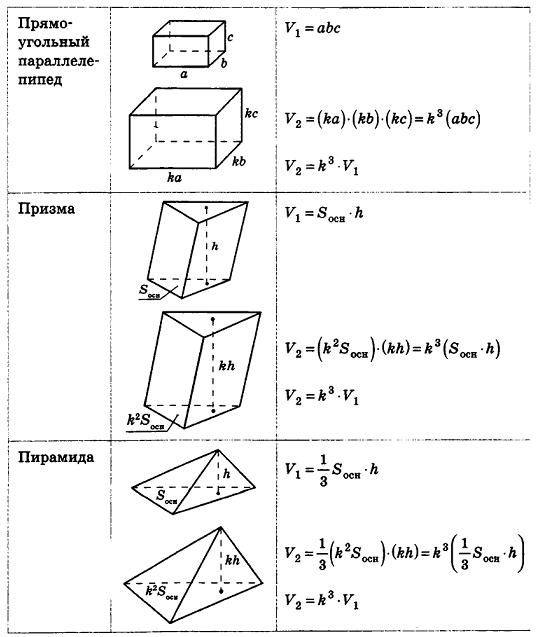
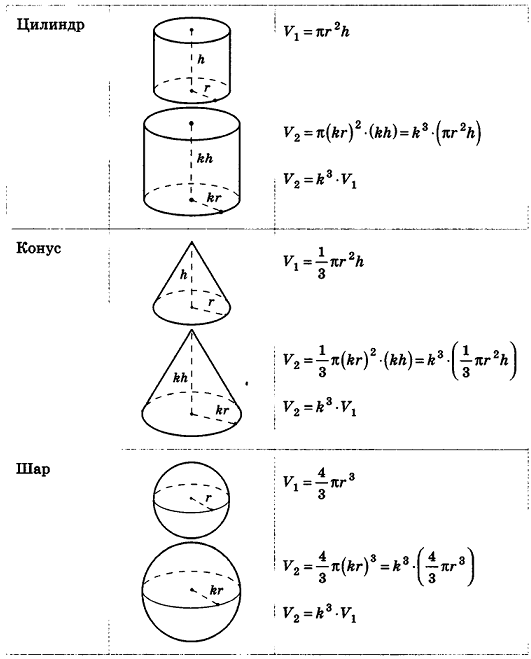
Кроме того, можно проследить за подобными с коэффициентом k многоугольниками на плоскости. Как известно, их периметры отличаются в k раз, площади — в k2 раз. Естественно предположить, что объемы подобных с коэффициентом k пространственных тел отличаются к3 раз. Проверим это для тел, формулы объема которых нам уже известны.
Итак, для всех рассмотренных тел верно следующее утверждение: объемы тел, подобных с коэффициентом k, относятся как k3.
Этот факт верен и для любых простых тел, то есть тел, которые можно разбить на конечное число треугольных пирамид. В частности, любые многогранники, подобные с коэффициентом к, имеют объемы, которые отличаются в k3 раз.
Пример №5
Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды?
Решение:
Пусть дана пирамида с вершиной S и высотой SO. Плоскость, параллельная основанию пирамиды, пересекает SO в точке 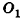
По условию = 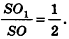
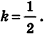
Ответ: 1:7.
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.
Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.
Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).
Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.
Затем по (3.2) вычислим их векторное произведение:
Модуль этого векторного произведения равен |AB×AC| = √((—1)2 + (—5)2 + 132) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #
Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.
Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).
Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов:
План урока:
Понятие объема
Свойства объема
Объем куба и прямоугольного параллелепипеда
Объем прямой призмы
Объем цилиндра
Понятие объема
Понятие объема появилось у человечества задолго до того, как геометрия оформилась как строгая наука. Многие вещества и товары, такие как зерно, рис и вода, необходимо хранить и транспортировать в различных упаковках (сосуды, бочки, ящики, контейнеры). При этом разные емкости могут вместить разное количество товаров. Например, пусть есть бочка, имеющая форму цилиндра, и контейнер, выглядящий как прямоугольный параллелепипед:
Предположим, что в бочку можно поместить 5 кг пшеницы, а в контейнер помещается уже 15 кг пшеницы, то есть в контейнер можно положить в 3 раза больше пшеницы, чем в бочку. Можно сказать, что вместимость контейнера втрое больше вместимости бочки. Однако измерять вместимость емкости с помощью массы пшеницы, помещаемой в него, неудобно, ведь в них можно класть и другие вещества. Мы можем положить в емкости что-нибудь более тяжелое, например сухой песок. Тогда в бочку может влезть уже 10 кг песка, а в контейнер – 30 кг. И снова получается, что вместимость контейнера втрое больше, хотя масса вещества увеличилась.
Именно для измерения вместимости и было введено понятие объема. Если в одну упаковку помещается вдвое больше товаров, чем во вторую упаковку, то и объем у нее будет вдвое больше. С древнейших времен замечено, что отношение объемов двух сосудов не зависит от того вещества, которое в них хранят. Например, если в один сосуд помещается в 5 раз больше риса, чем в другой сосуд, то в него также будет помещаться в 5 раз больше воды, в 5 раз больше песка, в 5 раз больше нефти и т. д. Таким образом, в практическом смысле объем – это количественная характеристика вместимости тех или иных упаковок.
В рамках стереометрии изучаются не реальные сосуды, а абстрактные тела. Каждое из них занимает определенную часть пространства, большую или меньшую. Объем используется для измерения этих частей пространства. Для обозначения объема используется латинская буква V.
Для измерения объема необходима единица измерения. Условно принимается, что куб, чьим ребром является единичный отрезок, имеет объем, равный единице. Такой куб именуется единичным. Заметим, что грани единичного куба – это единичные квадраты.
В случае, когда длина ребра куба является безразмерной величиной, то объем также будет безразмерной величиной. Если же указана единица измерения длины, то объем куба будет измеряться этой же единицей, к которой приписано слово «кубический». Например, если ребро куба равно 1 м, то объем куба будет равен 1 кубическому метру, или 1 м3. Объем куба с ребром 1 мм будет составлять 1 мм3 и т. д.

Свойства объема
Свойства объема во многом совпадают со свойствами площади. Ясно, что у равных тел будут одинаковы и объемы.
Второе свойство объема связано с тем, что он является аддитивной величиной. Это значит, что если тело можно разбить на несколько тел, то его объем будет равен сумме объемов этих тел.
Это свойство аддитивности объема уже позволяет решать некоторые стереометрические задачи.
Задание. Тело состоит из цилиндра объемом 12 см3 и конуса объемом 4 см3. Каков объем этого тела?
Решение. Здесь надо просто сложить объемы цилиндра и конуса, чтобы найти общий объем всей фигуры:
Ответ: 16 см3.
Задание. Найдите объем фигуры, показанной на рисунке:
Решение. Данную фигуру несложно разбить на три единичных куба:
Тогда объем тела будет равен сумме объемов трех единичных кубов, то есть трем:
Ответ: 3.
Задание. Вычислите объем фигуры, получающейся при рассечении куба плоскостью, проходящей через два его ребра.
Решение. Ясно, что такая секущая плоскость будет делить куб на две равные фигуры (иначе просто не удастся провести плоскость через два ребра):
Также понятно, что два получившихся многогранника равны друг другу. Обозначим объем каждого из них как V. Тогда в сумме их объем должен быть равен 1, ведь вместе эти фигуры образуют единичный куб. Это позволяет составить уравнение, из которого можно вычислить величину V:
Объем куба и прямоугольного параллелепипеда
Докажем важную вспомогательную теорему:
Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как VР, а большего – как VK:
Нам надо доказать, что объемы фигур пропорциональны их высотам:
Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что
где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:
В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом VK. Поэтому объем одной такой пластины равен величине VK/n:
Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:
Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:
(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).
Умножим это неравенство на длину АК:
Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:
Объем параллелепипеда с высотой АЕ обозначим как VЕ. Ясно, что
ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.
Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:
- единичный куб;
- параллелепипед с габаритами а, 1, 1 с объемом V1;
- параллелепипед с габаритами а, b, 1 с объемом V2;
- параллелепипед с габаритами а, b, c с объемом V.
Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:
Соответственно, для расчета объема параллелепипеда используется формула
Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.
Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?
Решение. Здесь надо просто перемножить габариты параллелепипеда:
Ответ: 252 см3.
Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.
Задание. Вычислите объем куба с ребром 8 метров.
Решение. Просто возводим сторону ребро куба в третью степень:
Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?
Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:
Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.
Ответ: 3 дм.
Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:
Тогда объем этого куба можно посчитать так:
Аналогично можно переводить и другие единицы измерения.
Объем прямой призмы
Рассмотрим сначала прямую призму, в чьем основании располагается прямоугольный треугольник. Ее можно достроить до прямоугольного параллелепипеда:
Ясно, что объем параллелепипеда будет вдвое больше объема исходной призмы, ведь он состоит из двух таких призм. Аналогично и площадь основания у параллелепипеда будет вдвое больше. Обозначим площадь основания призмы буквой S, а ее высоту как h, тогда площадь основания параллелепипеда будет 2S, а его объем составит 2S•h. Тогда объем призмы будет вдвое меньше, то есть он окажется равным S•h.
Далее рассмотрим прямую призму, в основании которой лежит уже произвольный треугольник. Проведем в этом треугольнике высоту, которая упадет на противоположную сторону (такую высоту всегда можно провести). Далее через эту высоту проведем плоскость, перпендикулярную основанию. В результате мы разделим призму на две прямых призмы, в основании каждой из которых будет лежать прямоугольный треугольник:
Пусть площади получившихся прямоугольных треугольников обозначены как S1и S2, а общая площадь основания исходной призмы – это S. Мы можем вычислить объемы этих призм:
Теперь, наконец, рассмотрим прямую призму, чье основание – произвольный многоугольник. Этот многоугольник можно разбить на несколько треугольников с площадями S1, S2, S3…, а призма соответственно будет разбита на несколько треугольных призм с объемами V1, V2, V3 и. т. д.
Объем каждой треугольный призмы мы можем рассчитать:
Задание. Все ребра правильной шестиугольной призмы одинаковы, их длина обозначена буквой а. Найдите объем такой призмы.
Решение. Сначала необходимо найти площадь основания призмы, то есть площадь правильного шестиугольника. Напомним формулы для правильных многоугольников, изученные ещё в девятом классе:
Для вычисления объема надо лишь умножить полученную площадь на высоту призмы, а она также равна а:
Задание. В кубе АВСDА1В1С1D1 через середины ребер СD и BC проведено сечение, параллельное ребру СС1. Это сечение отсекает от куба треугольную призму, чей объем равен 19. Найдите объем куба.
Решение. Ясно, что и куб, и треугольная призма будут прямыми призмами, причем у них одинаковая высота СС1. Тогда можно утверждать, что отношение их объемов равно отношению площадей их оснований:
Пусть сторона АВ имеет длину а. Тогда площадь квадрата АВСD будет составлять а2. Отрезки ЕС и FC будут вдвое короче АВ, то есть их длина составляет a/2. ∆EFC – прямоугольный, и его площадь может быть рассчитана как половина произведения его катетов:
Объем цилиндра
Цилиндр не получится разбить на несколько призм, поэтому для вычисления его объема используется другой метод. Впишем цилиндр в правильную n-угольную призму. Одновременно построим и другую правильную n-угольную призму, которая сама будет вписана в цилиндр. Объем вписанной призмы обозначим как Vв, а объем описанной призмы как Vо. Объем самого цилиндра – это Vц. При этом высоты всех трех фигур одинаковы:
Ясно, что объем вписанной призмы меньше объема цилиндра, а тот в свою очередь меньше объема описанной призмы:
Теперь будем неограниченно увеличивать число n. При этом площади Sв и Sо будут стремиться к площади основания цилиндра, равной величине πr2, где r– радиус основания цилиндра. Это возможно лишь в том случае, если справедливо равенство
Задание. Найдите объем цилиндра с высотой 5 см и радиусом 6 см.
Решение. Сначала находим площадь основания:
Задание. Известно, что высота цилиндра вдвое больше его радиуса, а объем цилиндра равен 54π. Найдите радиус цилиндра.
Решение. Обозначим радиус цилиндра буквой х. Тогда по условию высота будет вдвое больше, то есть она составит 2х. Вычислим объем цилиндра:
Ответ: 3.
Задание. Труба изготовлена из металла с плотностью 11,4 г/см3. Внутренний диаметр трубы равен 13 мм, а ее стенка имеет толщину 4 мм. Длина трубы – 25 метров. Какова ее масса?
Решение. Для расчета массы необходимо сперва вычислить объем трубы. Ясно, что если к объему трубы прибавить объем внутреннего отверстия, то в итоге получится объем большого цилиндра, чей диаметр равен наружному диаметру трубы:
Легко найти объем отверстия, ведь оно имеет форму цилиндра. Его радиус вдвое меньше диаметра, то есть он равен 13/2 = 6,5 мм. При расчете важно не забыть перевести высоту в миллиметры:
Сегодня мы узнали о такой характеристике тел, как объем. Если объем куба и прямоугольного параллелепипеда мы умели находить ещё в средней школе, то определять объем цилиндра и прямой призмы мы научились только сейчас. Однако все эти случаи по сути одинаковы – надо перемножить высоту фигуры и площадь ее основания. В будущем мы научимся вычислять объемы более сложных фигур – пирамиды, конуса, шара.