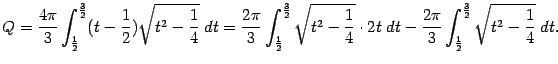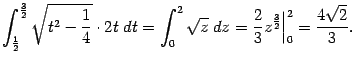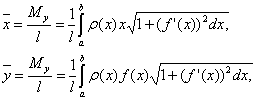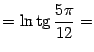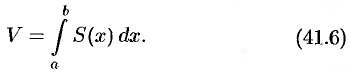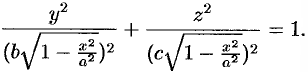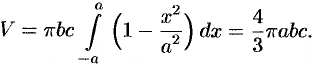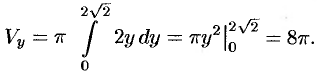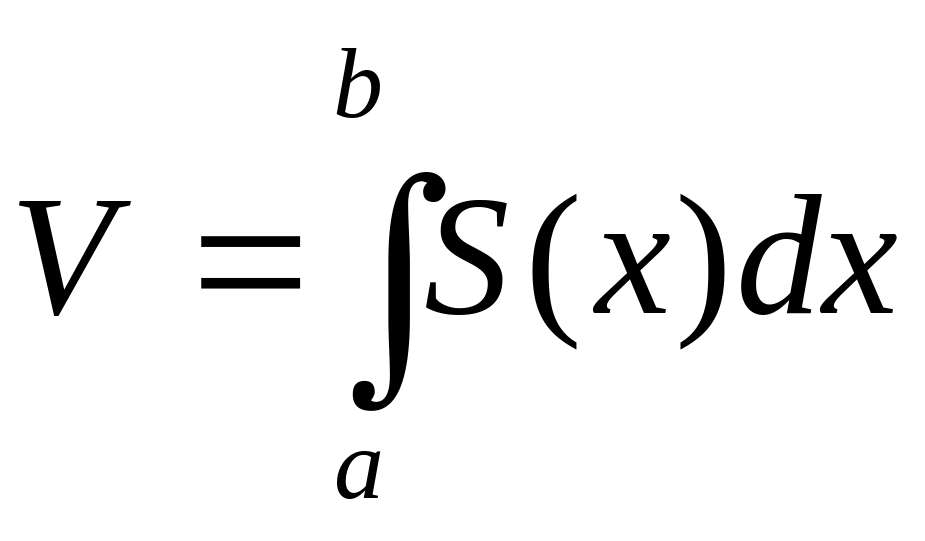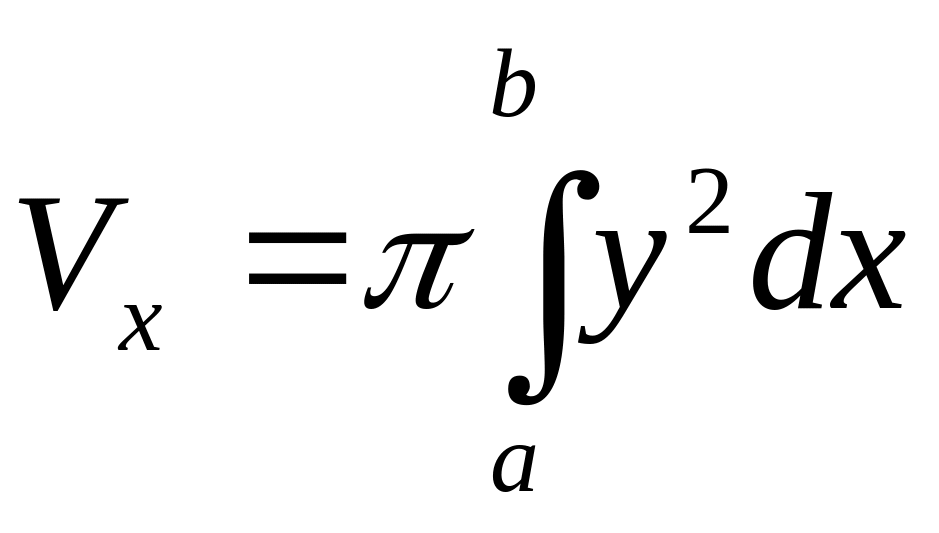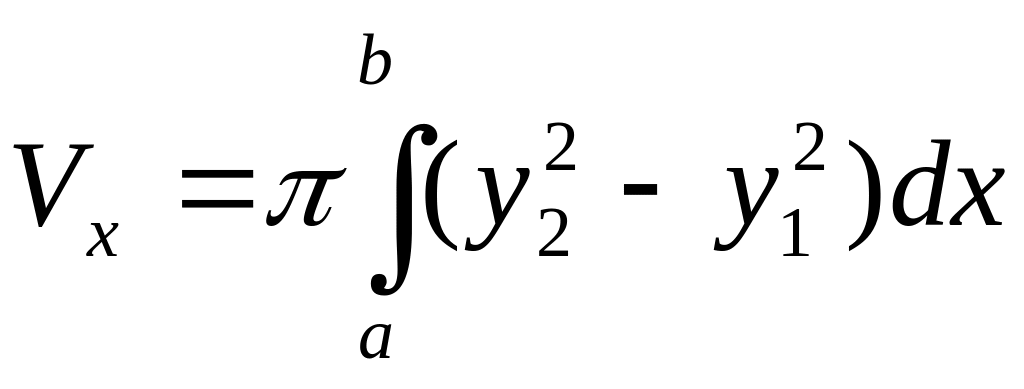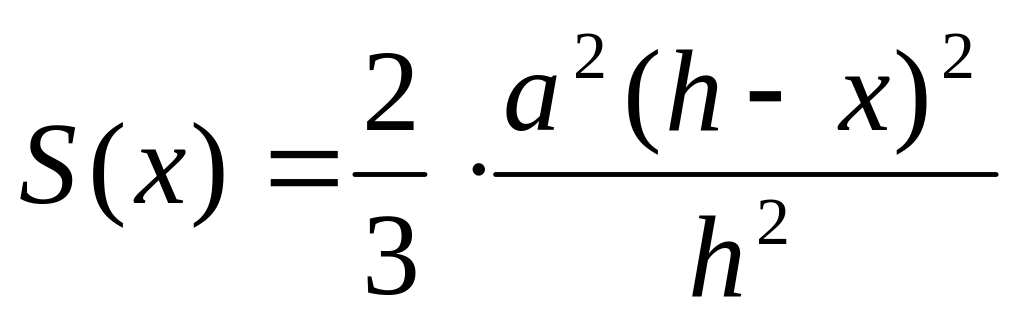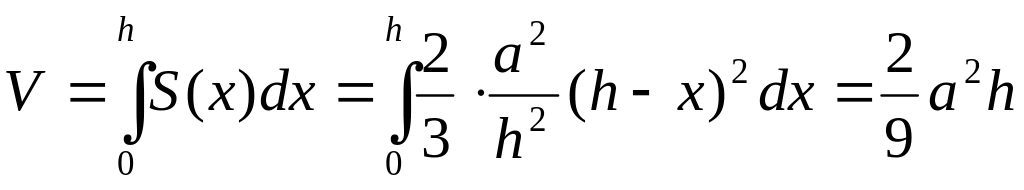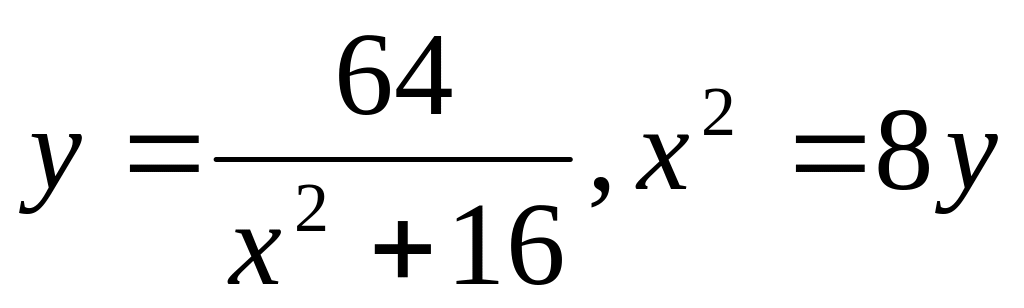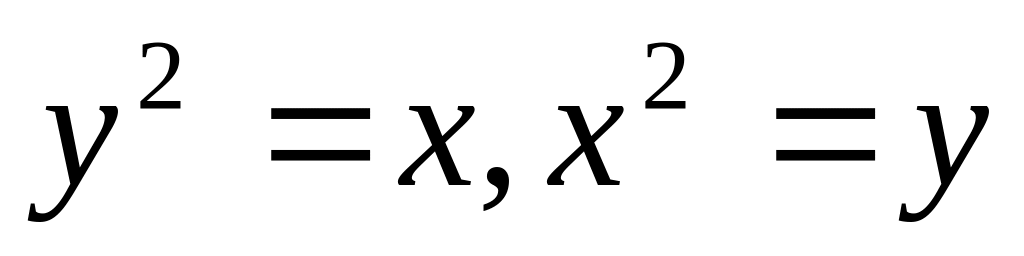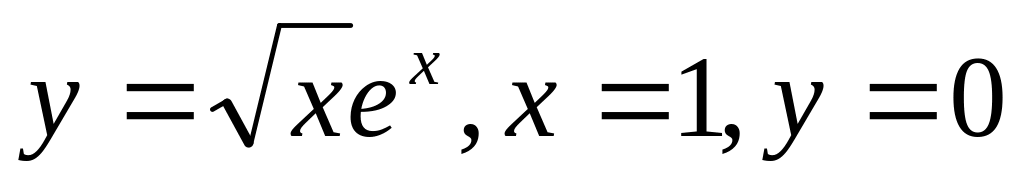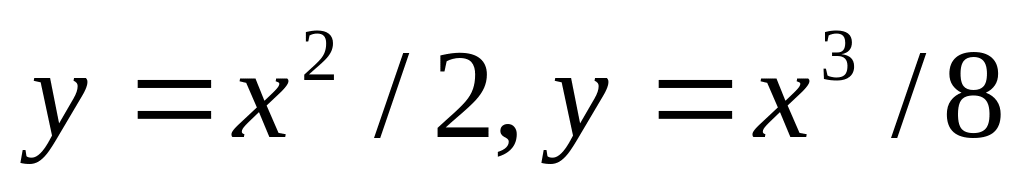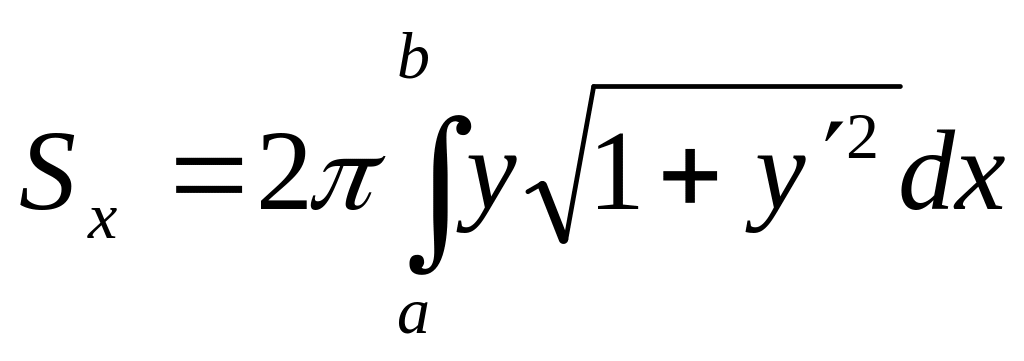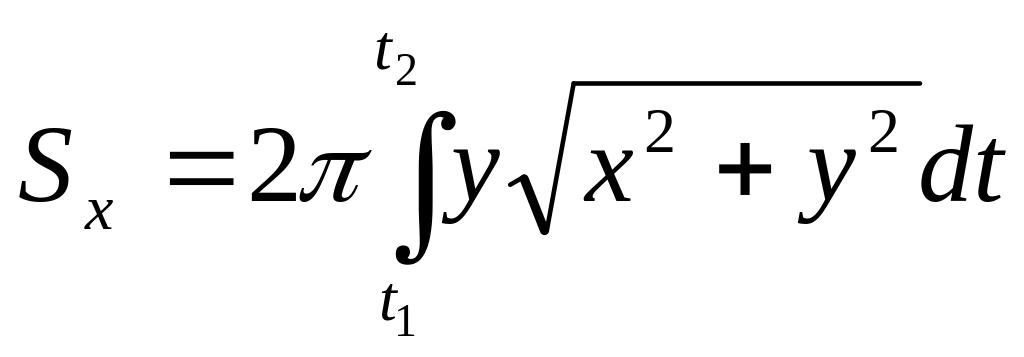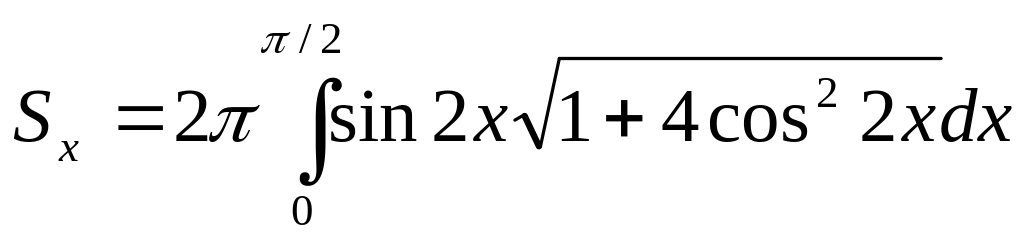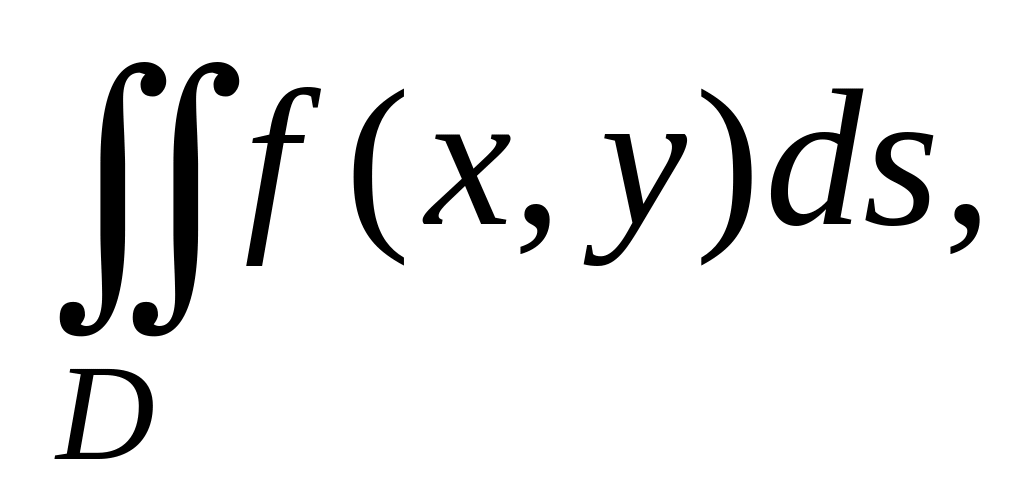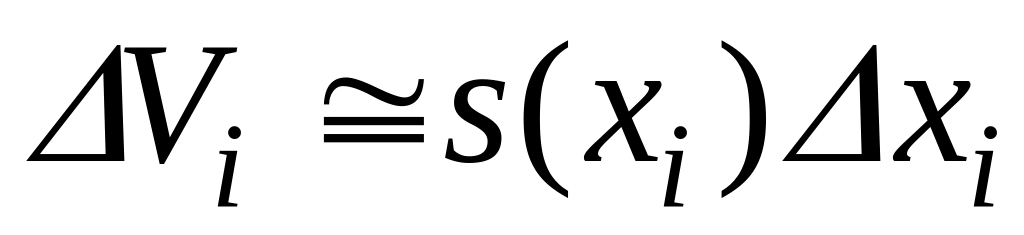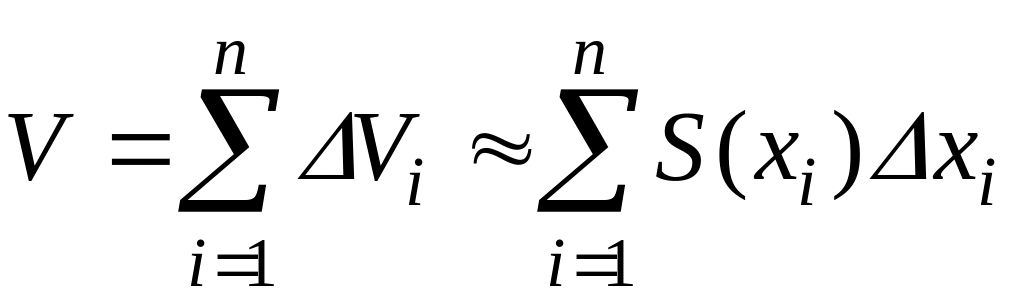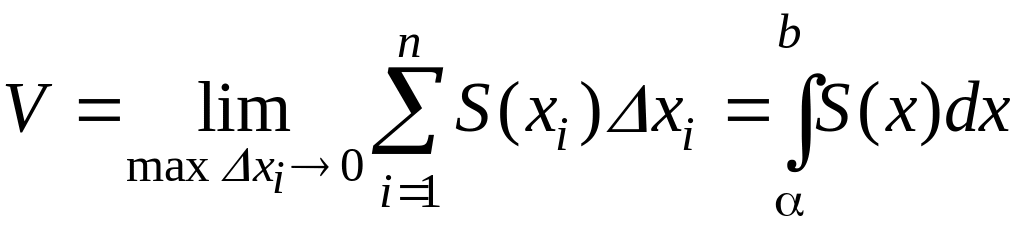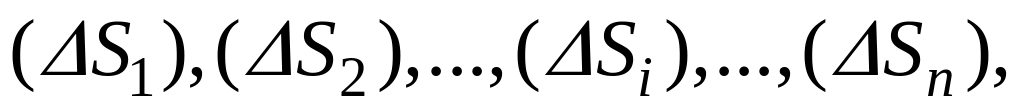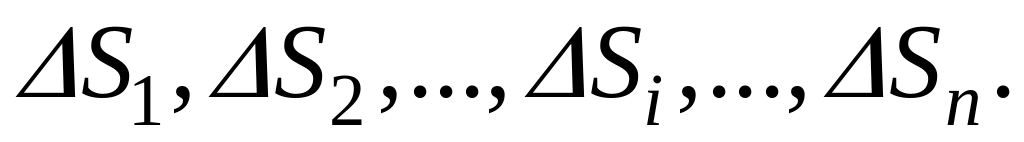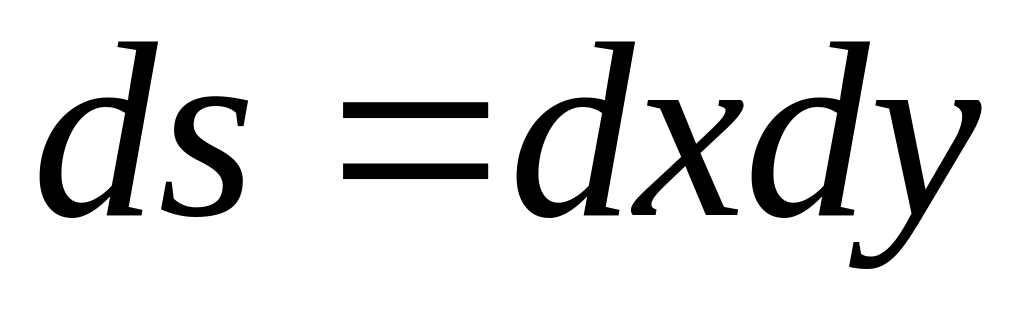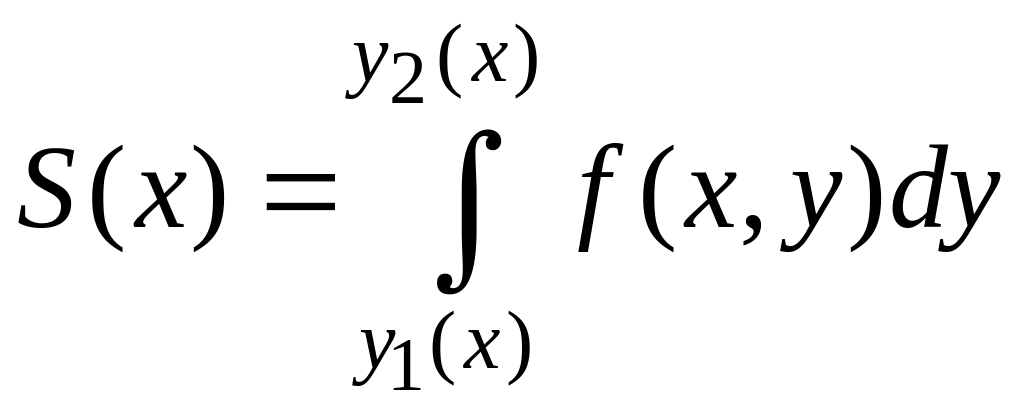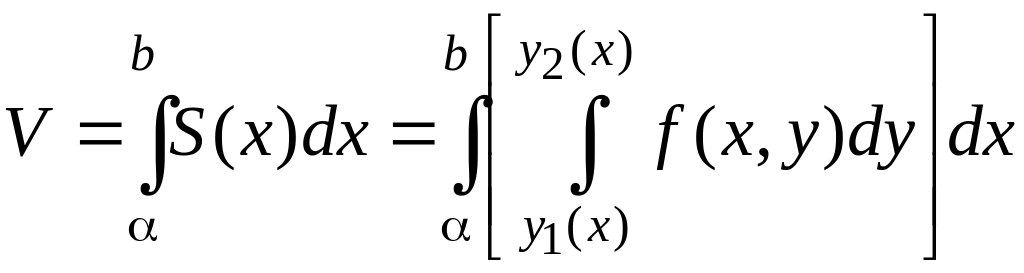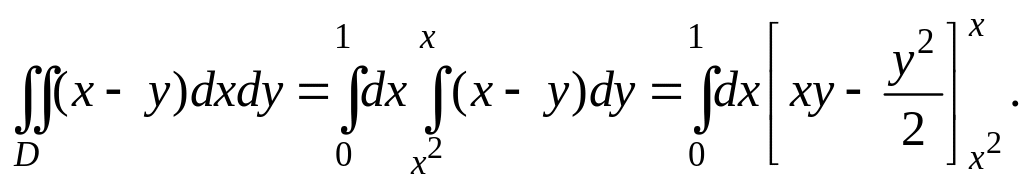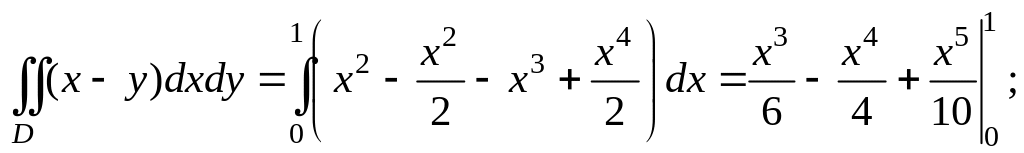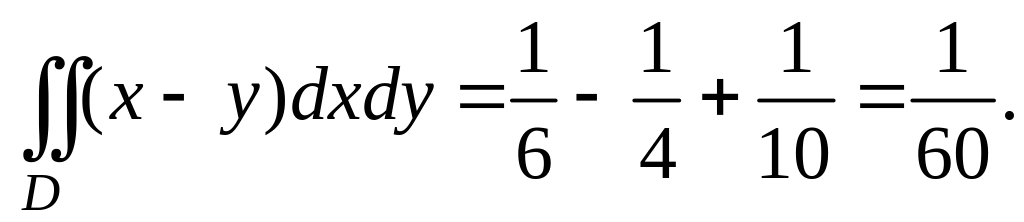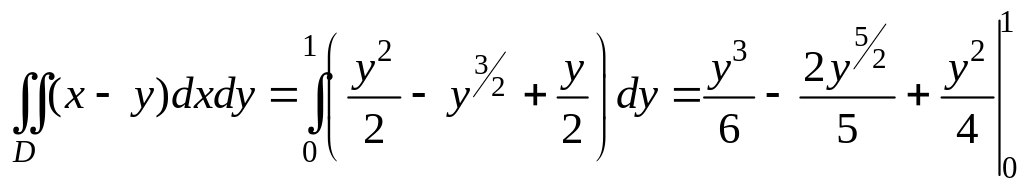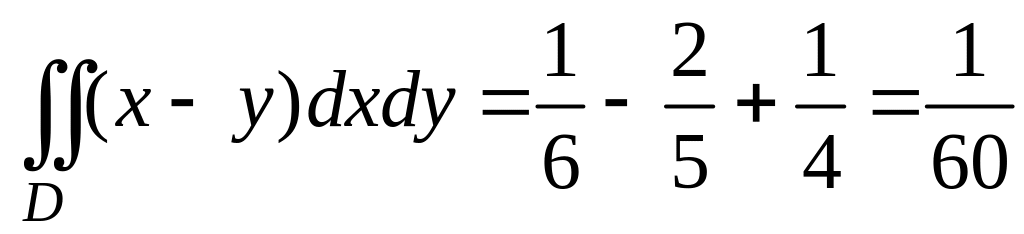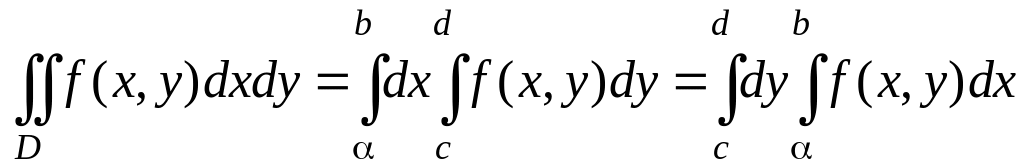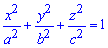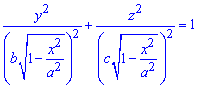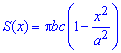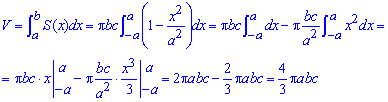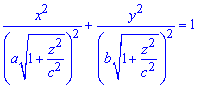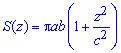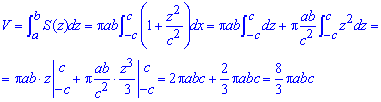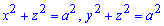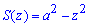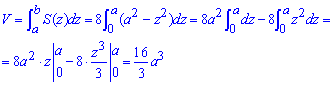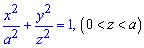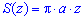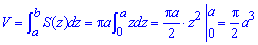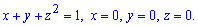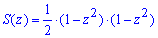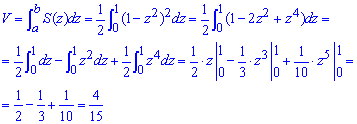Как найти объем если известна площадь сечения

Нахождение объёма тела по площадям поперечных сечений

П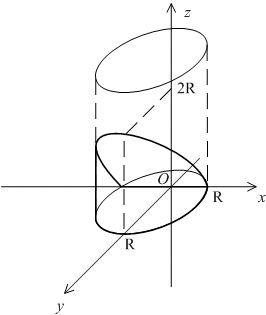усть
в пространстве задано тело. Пусть
построены его сечения плоскостями,
перпендикулярными осии проходящими через точкиx
на ней. Площадь фигуры, образующейся в
сечении, зависит от точки х,
определяющей плоскость сечения. Пусть
эта зависимость известна и задана
непрерывной на
функцией.
Тогда объем части тела, находящейся
между плоскостямих=а
и х=в
вычисляется по формуле

Пример.
Найдём объём ограниченного тела,
заключённого между поверхностью цилиндра
радиуса
:,
горизонтальной плоскостьюи наклонной плоскостьюz=2y
и лежащего выше горизонтальной плоскости
.

Очевидно, что
рассматриваемое тело
проектируется
на осьв
отрезок,
а приxпоперечное сечение тела представляет
собою прямоугольный треугольник с
катетамиy
и z=2y,
где y
можно выразить через x
из уравнения цилиндра:

Поэтому площадь
S(x)
поперечного сечения такова:

Применяя формулу,
находим объём тела
:

Вычисление объемов тел вращения

Пусть
на отрезке
[a,
b]
задана непрерывная знакопостоянная
функция y=f(x).
Объемы тела вращения, образованного
вращением вокруг оси Ох
(или оси Оу)
криволинейной трапеции, ограниченной
кривой y=f(x)
(f(x)0)
и прямыми у=0,
х=а, х=b,
вычисляются соответственно по формулам:

,
(19)

(20)

Если
тело образуется при вращении вокруг
оси Оу
криволинейной трапеции, ограниченной
кривойи прямымиx=0,
y=c,
y=d,
то объем тела вращения равен

.
(21)

Пример.
Вычислить объем тела, полученного
вращением фигуры, ограниченной линиями
вокруг осиОх.

По формуле (19)
искомый объем

(ед.²)

Пример.
Пусть в плоскости xOy
рассматривается линия y=cosx
на отрезке
.

Эта
линия вращается в пространстве вокруг
оси,
и полученная поверхность вращения
ограничивает некоторое тело вращения
(см. рис.). Найдём объёмэтого
тела вращения.

Согласно формуле,
получаем:

Площадь поверхности вращения

Если дуга кривой,
заданная неотрицательной функцией
,,
вращается вокруг осиOx,
то площадь поверхности вращения
вычисляется по формуле
,
гдеa
и b
— абсциссы начала и конца дуги.

Если дуга кривой,
заданная неотрицательной функцией
,,
вращается вокруг осиOy,
то площадь поверхности вращения
вычисляется по формуле

,

где с и d
— абсциссы начала и конца дуги.

Если дуга кривой
задана параметрическими
уравнениями
,,
причем,
то

Если дуга задана
в полярных
координатах
,
то

.

Пример.
Вычислим площадь поверхности, образованной
вращением в пространстве вокруг оси
части линииy=,
расположенной над отрезкомоси.

Так как
,
то формула даёт нам интеграл

Сделаем в последнем
интеграле замену t=x+(1/2)
и получим:

В первом из
интегралов правой части сделаем замену
z=t²—:

Для вычисления
второго из интегралов в правой части
обозначим его
и
проинтегрируем по частям, получив
уравнение для:

Перенося
в
левую часть и деля на 2, получаем

откуда, наконец,

Приложения определенного интеграла к решению некоторых задач механики и физики

Работа
переменной силы.
Рассмотрим
движение материальной точки вдоль оси
OX
под
действием переменной силы f
,
зависящей от положения точки
x
на оси, т.e. силы, являющейся функцией x.
Тогда работа A,
необходимая для перемещения материальной
точки из позиции x
= a
в позицию x
= b
вычисляется по формуле:

Для
вычисления силы
давления жидкости
используют закон Паскаля, согласно
которому давление жидкости на площадку
равно ее площади S,
умноженной на глубину погружения h,
на плотность ρ
и ускорение силы тяжести g,
т.е.

.

1.
Моменты
и центры масс плоских кривых.
Если дуга кривой задана уравнением
y=f(x), a≤x≤b, и имеет плотность
,
тостатические
моменты
этой дуги M_x
и M_y
относительно координатных осей Ox и Oy
равны

;

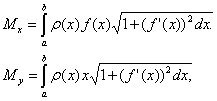
моменты
инерции
I_Х
и I_у
относительно тех же осей Ох и Оу
вычисляются по формулам

а
координаты
центра масс
и— по формулам

где l— масса дуги,
т. е.

Пример
1.
Найти статические моменты и моменты
инерции относительно осей Ох и Оу дуги
цепной линии y=chx при 0≤x≤1.

Если
плотность не указана, предполагается,
что кривая однородна и
.
Имеем:Следовательно,

Пример
2.
Найти координаты центра масс дуги
окружности x=acost, y=asint, расположенной в
первой четверти. Имеем:

Отсюда получаем:

В
приложениях часто оказывается полезной
следующая Теорема
Гульдена.
Площадь поверхности, образованной
вращением дуги плоской кривой вокруг
оси, лежащей в плоскости дуги и ее не
пересекающей, равна произведению длины
дуги на длину окружности, описываемой
ее центром масс.

Пример
3.
Найти координаты центра масс полуокружности

Вследствие
симметрии
.
При вращении полуокружности вокруг оси
Ох получается сфера, площадь поверхности
которой равна,
а длина полуокружности равна па. По
теореме Гульдена имеем 4

Отсюда
,
т.е. центр масс C имеет координаты C.

2.
Физические
задачи.
Некоторые применения определенного
интеграла при решении физических задач
иллюстрируются ниже в примерах .

Пример
4.
Скорость прямолинейного движения тела
выражается формулой
(м/с).
Найти путь, пройденный телом за 5 секунд
от начала движения.

Так
как путь,
пройденный телом
со скоростью v(t)
за отрезок времени [t₁,t₂],
выражается интегралом

то имеем:

П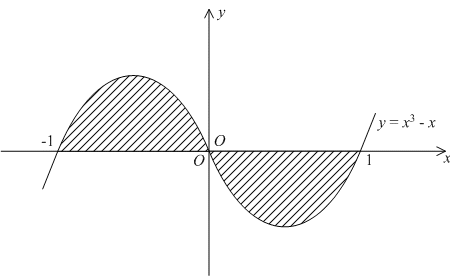ример. 
Найдём площадь
ограниченной
области, лежащей между осьюи
линиейy=x³-x.
Поскольку

линия пересекает
ось
в
трёх точка:x₁=-1,
x₂=0,
x₃=1.

Ограниченная
область между линией и осью
проектируется
на отрезок,причём на отрезке,линияy=x³-x
идёт выше оси
(то
есть линииy=0,
а на
— ниже. Поэтому площадь области можно
подсчитать так:

Пример.
Найдём площадь
области,
заключённой между первым и вторым витком
спирали Архимедаr=a
(a>0)
и отрезком горизонтальной оси
.

Первый виток
спирали соответствует изменению угла
в
пределах от 0 до,
а второй — отдо.
Чтобы привести изменение аргументак одному промежутку, запишем уравнение
второго витка спирали в виде,
.
Тогда площадь
можно
будет найти по формуле, положиви
:

Пример.
Найдём объём
тела,
ограниченного поверхностью вращения
линииy=4x-x²
вокруг оси
(при).

Для вычисления
объёма тела вращения применим формулу

Имеем:

Пример.
Вычислим длину
дуги
линииy=lncosx,
расположенной между прямыми
и.

Так как

и

(мы взяли в качестве
значения корня
,
а не -cosx,
поскольку cosx
>0 при
,
длина дуги равна

Ответ:
.

Пример.
Вычислим площадь Q
поверхности вращения, полученной при
вращении дуги циклоиды x=t-sint
; y=1-cost,
при
,
вокруг оси.

Для
вычисления применим формулу:

Имеем:
, так что

Для перехода под
знаком интеграла к переменной
заметим,
что приполучаем,
а также

Кроме того,
предварительно вычислим

(так что)
и

Получаем:

Делая замену
,
приходим к интегралу

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

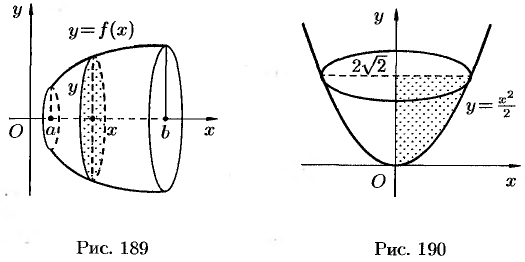
Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

Пусть требуется найти объем тела, причем известны площади сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси : , .

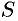
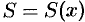
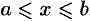
Применим схему II (метод дифференциапа).

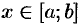
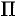
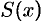
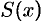
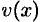
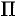
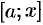
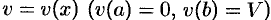
1. Через произвольную точку проведем плоскость , перпендикулярную оси (см. рис. 187). Обозначим через площадь сечения тела этой плоскостью; считаем известной и непрерывно изменяющейся при изменении . Через обозначим объем части тела, лежащее левее плоскости . Будем считать, что на отрезке величина есть функция от , т. е. .

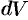
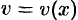
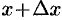
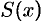
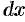
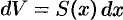
2. Находим дифференциал функции . Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось в точках и , который приближенно может быть принят за цилиндр с основанием и высотой . Поэтому дифференциал объема .

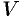
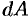
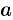
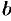
3. Находим искомую величину путем интегрирования в пределах от до :

Полученная формула называется формулой объема тела по площади параллельных сечений.

Пример №41.6.

Найти объем эллипсоида .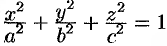

Решение:

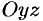
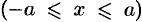
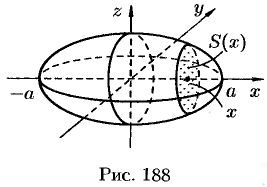
Рассекая эллипсоид плоскостью, параллельной плоскости и на расстоянии от нее , получим эллипс (см. рис. 188):

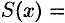
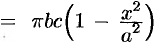
Площадь этого эллипса равна . Поэтому, по формуле (41.6), имеем

Объем тела вращения

Пусть вокруг оси вращается криволинейная трапеция, ограниченная непрерывной линией , отрезком и прямыми и (см. рис. 189). Полученная от вращения фигура, называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси , проведенной через произвольную точку оси (), есть круг с радиусом . Следовательно, .

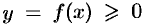
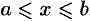
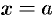
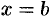
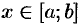
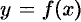
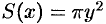
Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

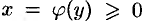
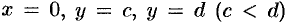
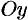
Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми , то объем тела, образованною вращением этой трапеции вокруг оси , по аналогии с формулой (41.7), равен

Пример №41.7.

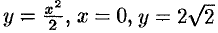
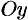
Найти объем тела, образованною вращением фигуры, ограниченной линиями вокруг оси (см. рис. 190).

Решение:

По формуле (41.8) находим:

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

§ 5. Вычисление объема тела

1. Вычисление объема тела по известным площадям поперечных сечений.

Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть выражена как функция от х, т. е, в виде S = S(x), a≤x≤b_t то объем части тела, заключенной между перпендикулярными оси Ох плоскостями х = а и x = b, находится по формуле

2. Вычисление объема тела вращения. Если криволинейная трапеция, огра­ниченная кривой y = f(x) и прямыми y = 0, х = а, x = b, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле

х = b, вращается вокруг оси Ох, то объем тела вращения

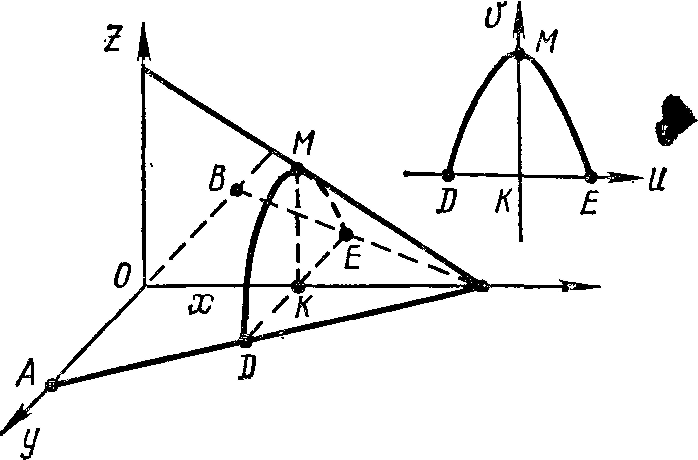
1626. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривой у 2 = (х— 1) 3 и прямой х = 2 (рис. 43).

Рис. 43

(куб. ед.)

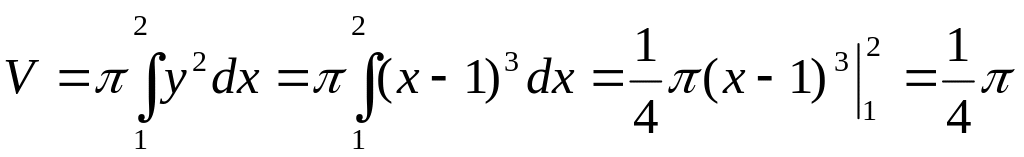
1627. Найти объем тела, в основании которого лежит равнобед­ренный треугольник с высотой h и основанием а. Поперечное сече­ние тела есть сегмент параболы с хордой, равной высоте сегмента (рис. 44).

Решение. Имеем |AВ| = a, |ОС| =h, |MK| = |DE|, |OK|=x. Выразим площадь поперечного сечения как функцию от х, для чего предварительно найдем уравнение параболы. Длину хорды DE можно найти из подобия соответствующих треугольников, а именно:

Положим |DE|=m, тогда уравнение параболы в системе координат uKv примет вид v= m-(4/m)u 2 . Отсюда находим площадь поперечного сечения данного тела:

или

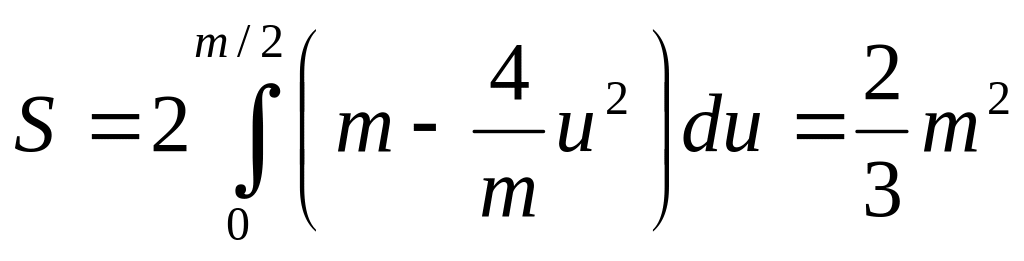
Найти объемы тел, образованных вращением вокруг оси Ох фигур, ограниченных линиями:

1628.

1629.

1630.

1631.

1632. Найти объем тела, ограниченного плоскостями х = 1,х = 3, если площадь его поперечного сечения обратно пропорцио­нальна квадрату расстояния сечения от начала координат, а при х = 2 площадь сечения равна 27 (кв. ед.)

1633. Найти объем цилиндрического клина по его размерам, указанным на (задача Архимеда).

1634. В цилиндрический стакан с водой вложен параболоид вра­щения вершиной вниз. Основание и высота параболоида совпадают с основанием и высотой цилиндра. Найти объем оставшейся в ста­кане воды, если радиус основания равен r, а высота равна h.

§ 6. Вычисление площади поверхности вращения

Если дуга гладкой кривой у = f (х) (а≤х≤b) вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле

1635. Найти площадь поверхности, образованной вращением вокруг оси Ох дуги синусоиды у= sin2x от х = 0 до х = π/2.

Решение. Находим y’ = 2 cos 2x; тогда

(кв. ед.).

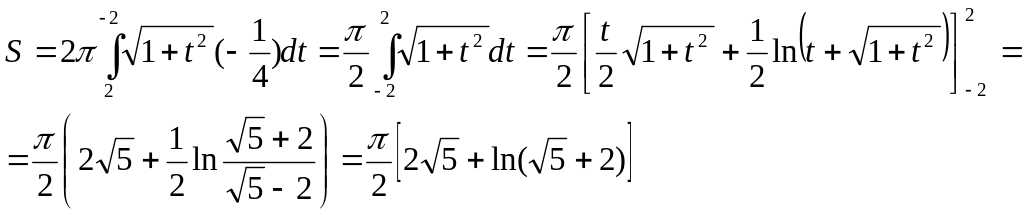
Найти площади поверхностей, образованных вращением вокруг оси Ох дуг кривых:

Источник

3.9.3. Объем тел с известным поперечным сечением

Двойной интеграл по плоской области D, от заданной на ней функции записывают так:

где ds – мера бесконечно малых элементов области D. Вычисление двойного интеграла сводят к последовательному вычислению двух линейных интегралов по переменным x и y. Чтобы получить формулу перехода к линейным интегралам, решим задачу о вычислении объема тела с известным поперечным сечением.

Рассмотрим тело произвольной формы (Рис.3.9.1), у которого площадь поперечных сечений, перпендикулярных оси абсцисс, есть известная функция от x:

S 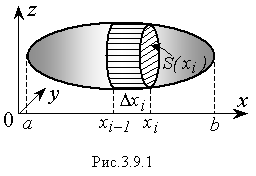= S(x).

Нужно найти объем этого тела. Спроектируем крайние точки тела на ось Ox. Пусть их координаты равны х = α, х = b.

Далее, разобьем тело плоскостями, перпендикулярными оси Ox, на n – частей.

Объем i-ой части (Рис. 3.9.1) можно приближенно принять за объем прямого цилиндра с высотой Δx_i и основанием S(x_i):

Тогда объем всего тела приближенно будет равен сумме объемов элементарных частей:

Точное значение объема получают в пределе, который дает линейный интеграл от функции S(x) на интервале [α,b]

Таким образом, объем тела произвольной формы можно найти с помощью линейного интеграла, если известен закон изменения площади его поперечного сечения, т.е. известна функция S(x).

3.9.4. Вычисление двойного интеграла путем сведения к линейному

Требуется вычислить двойной интеграл от функции z = f(x,y) по правильной плоской области D:

(3.9.1)

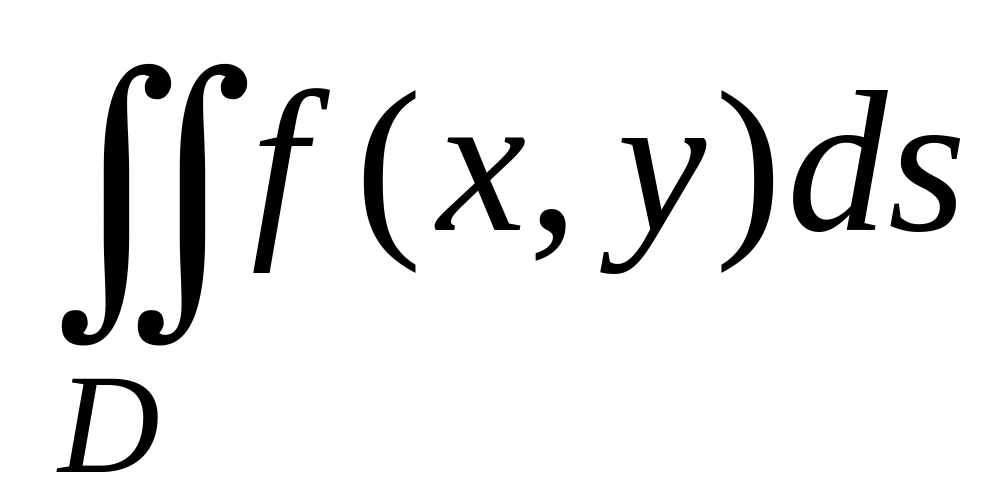
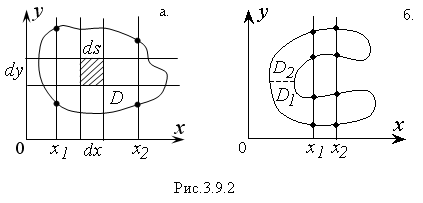
Область D называют правильной, если прямые, параллельные координатным осям, пересекают ее границу не более чем в двух точках (Рис. 3.9.2а). Неправильную область можно разбить на части и представить как объединение правильных областей, например D₁ и D₂ (Рис.3.9.2б).

Плоскую область D правильной формы считают заданной, если известны уравнения ограничивающих ее линий.

Напомним, что элементарные части (элементарные области), на которые разбивают область D при составлении интегральной суммы, были обозначены в круглых скобках:

а их меры (площади) тем же символом без круглых скобок:

Найдем удобное выражение для меры элемента области – ds.

Для этого разобьем D на элементарные части прямыми, параллельными координатным осям (Рис.3.9.2а). Тогда мера элементарной части будет равна площади прямоугольника:

и двойной интеграл (3.9.1) можно записать так:

(3.9.2)

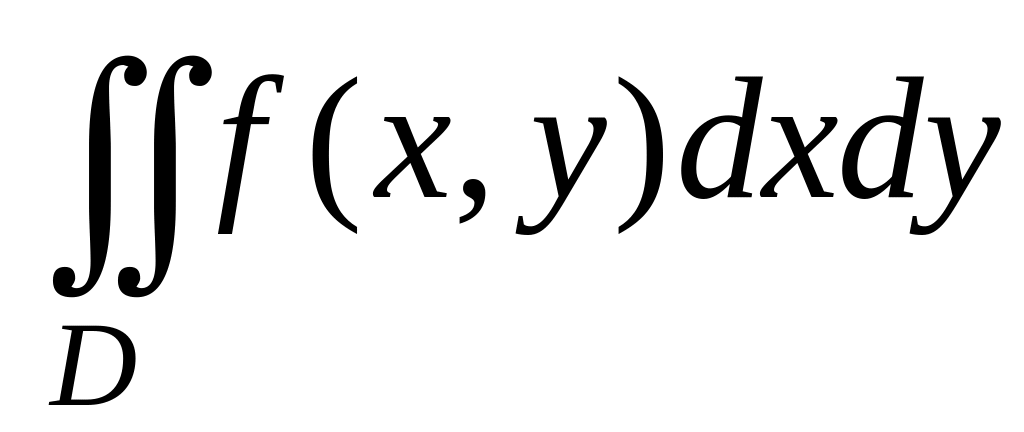
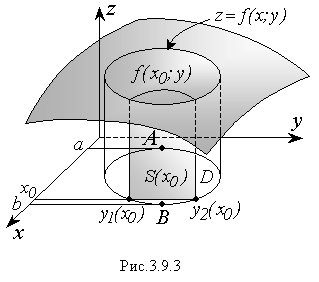
Известно, что двойному интегралу дают геометрическую интерпретацию: он равен объему цилиндрического тела, основанием которого является область D, а сверху это тело ограничено графиком подынтегральной функции z = f(x,y) (Рис. 3.9.3). Следовательно, задачу о вычислении двойного интеграла можно свести к задаче вычисления объема тела с известным поперечным сечением. Найдем объем цилиндрического тела, изображенного на рисунке 3.9.3, по формуле:

(3.9.3)

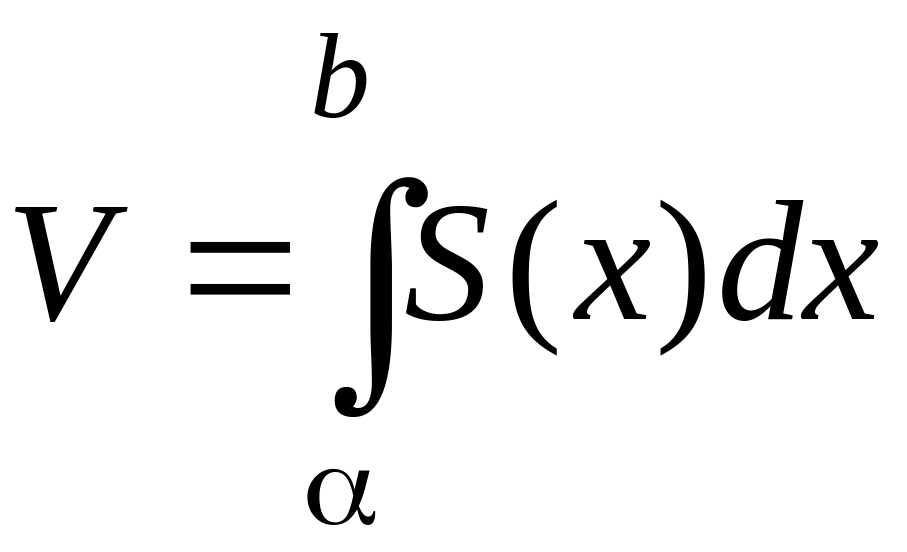
Для этого, спроектируем крайние точки А и В основания цилиндра (области D) на ось Ох, в результате получим отрезок [α,b], в пределах которого изменяется переменная х. При этом точки А и В делят границу области D на две линии. Пусть уравнения этих линий соответственно равны: y₁(x); y₂(x), тогда переменная y внутри D будет изменятся от своих значений на линии y₁(x) до значений на y₂(x).

Рассечем тело плоскостью х = х₀, перпендикулярной оси Ох. В сечении получим криволинейную трапецию, ограниченную сверху линией пересечения графика подынтегральной функции z = f(x,y) и плоскости х = х₀. Уравнением этой линии является функция одного аргумента

где х₀ = const, y – независимая переменная.

Площадь полученной криволинейной трапеции равна линейному интегралу:

(3.9.4)

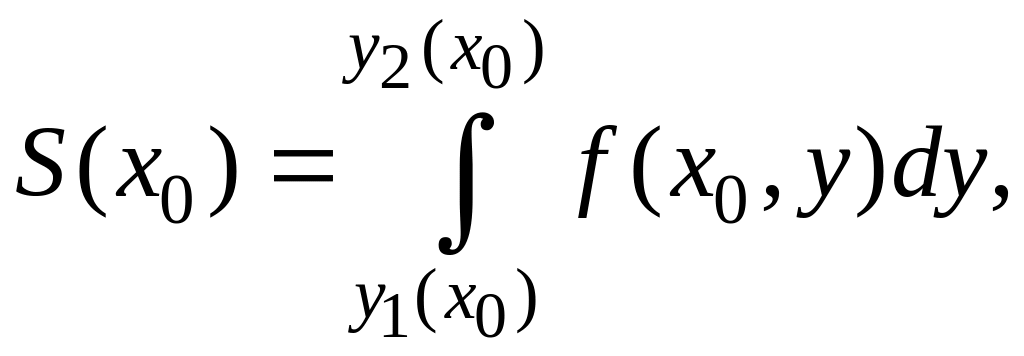
у которого нижний предел y₁(x₀) – есть точка входа прямой х = х₀ в область D, а верхний предел y₂(x₀) – точка ее выхода. Очевидно, что при изменении х₀ внутри отрезка [α,b] будет изменятся площадь соответствующего ему поперечного сечения, вычисляемая по формуле (3.9.4). Иными словами, площадь поперечного сечения цилиндрического тела есть функция от x (индекс 0 можно опустить) вида:

и поэтому объем этого тела, можно найти по формуле (3.9.3) т.е.:

Так как найденный объем равен двойному интегралу, то окончательно получим:

(3.9.5)

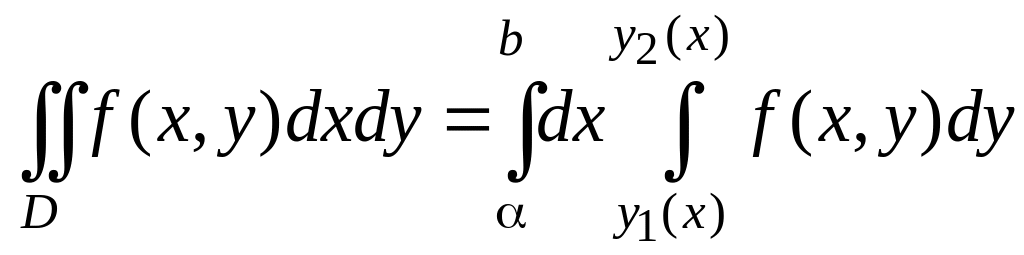
Из формулы (3.9.5) следует, что вычисление двойного интеграла свелось к последовательному вычислению двух линейных интегралов. Внутренний интеграл берут по переменной y, при этом x – считают постоянной. После нахождения первообразной и подстановки пределов во внутреннем интеграле остается одна переменная x, по которой вычисляют внешний интеграл.

Порядок интегрирования в выражении (3.9.5) можно менять местами. Чтобы внешний интеграл вычислялся не по x, как следует из формулы (3.9.5), а по переменной y, нужно область D спроектировать на ось Оy. Тогда проекции ее крайних точек дадут постоянные пределы во внешнем интеграле для y. Внутренний же интеграл следует вычислять по переменной x, при этом пределы у этой переменной будут зависеть от у.

Таким образом, у внешнего интеграла в обоих случаях пределы постоянны, они равны проекциям крайних точек области на соответствующую координатную ось.

Последовательное вычисление двух линейных интегралов называют двукратным интегрированием.

Следует отметить, что основная трудность при сведении двойного интеграла к двукратному заключается в расстановке пределов во внутреннем интеграле, которые в большинстве случаев переменные. Поэтому сначала строят область D и выбирают координатную ось, на которую проектируют область. Затем находят проекции (α,b) крайних точек области на эту ось и по чертежу определяют переменные пределы для внутреннего интеграла.

Пример 1. Вычислить двойной интеграл от функции f(x,y) = x – y по области D, ограниченной линиями: y = x 2 , y = x.

Р 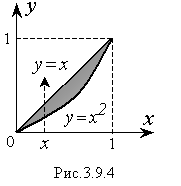ешение. Спроектируем построенную область на ось Oх (Рис. 3.9.4). Точки пересечения графиков функций y = x 2 и y = x – есть крайние точки области. Найдем их проекции:

Таким образом, внутри области D переменная x изменяется от 0 до 1. Пределы изменения второй переменной y будут зависеть от x. Чтобы найти их, проведем прямые параллельные оси Оy, пересекающие область D. Эти прямые для различных значений x входят в область на линии y = x 2 и выходят из области на линии y = x (Рис.3.9.4). Следовательно, переменная y внутри области изменяется от значений на линии y = x 2 до значений на линии y = x.

Подставляя вместо y верхний и нижний пределы, получим:

Как отмечалось выше, чтобы внешний интеграл вычислялся по переменной y, нужно область D спроектировать на ось Oy. Найдем проекции крайних точек области на эту ось:

(Рис. 3.9.4).

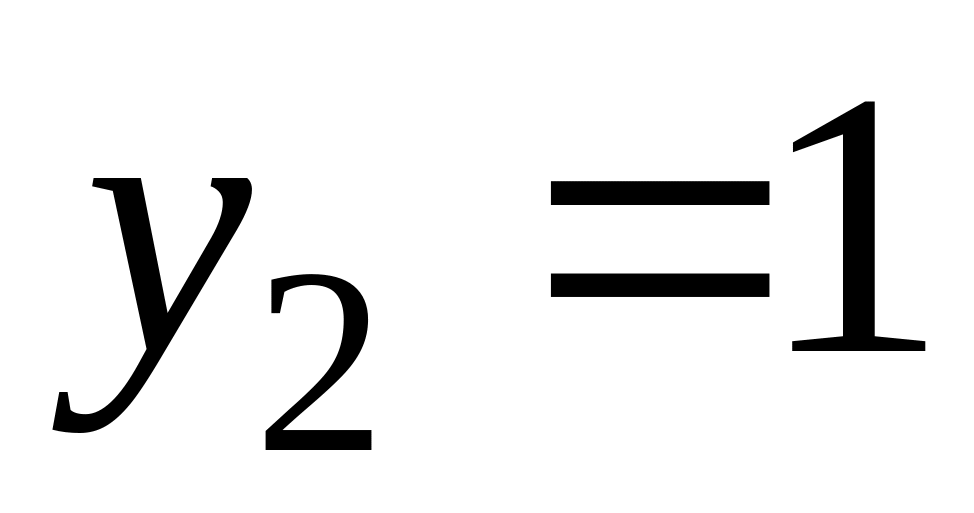
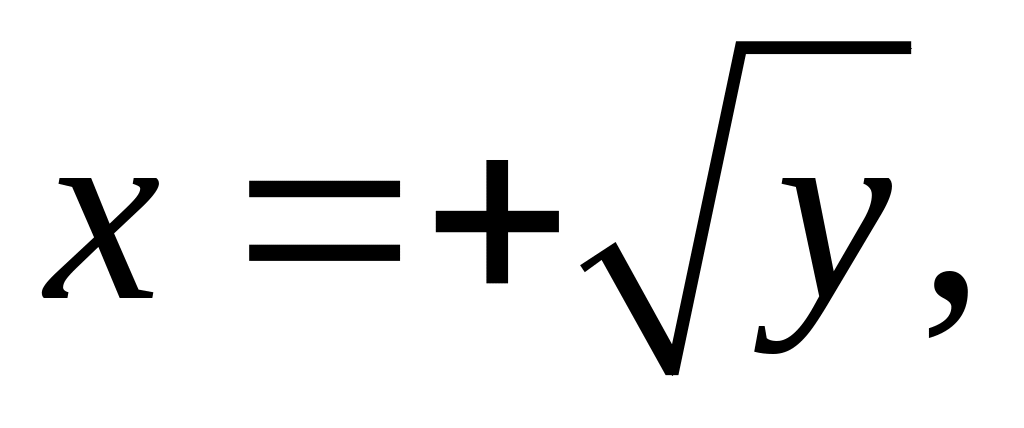
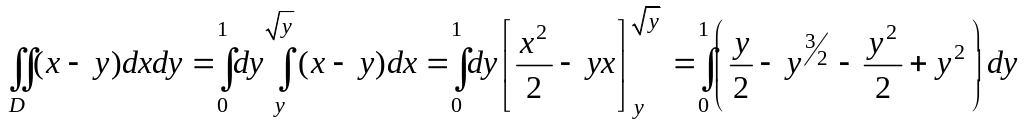
Тогда значения переменной x в области D будут изменятся от ее значений на уравнении прямой x = y до ее значений на уравнении параболы, решенной относительно x: следовательно:

В обоих случаях результат вычислений один и тот же.

Когда область D является прямоугольником со сторонами, параллельными координатным осям (Рис.3.9.5), пределы становятся постоянными не только внешнего, но и внутреннего интегралов. В этом случае формулы приведения двойного интеграла к двукратному интегрированию становятся очень простыми:

т.е. порядок интегрирования можно брать любой.

Источник

Для определения объема цилиндра надо знать величины Н и D .

Из чертежа видно Н = СВ,а D =2*Н (углы в треугольнике АСВ 60° и 30°).

Известно из данных S=64 осевого сечения.Понятно что стороны сечения раны высоте и диаметру цилиндра и соотношение их 1:2.

Определим величену (1). ОО¹СВ = 64:2=32 =ОВ*СВ;и ОВ = СВ =32^ =5,6568.

СВ =5,65685

D =11,313708

Проверим.11,313708*5­,65685=63,9999.

Определим объем: D²*3,14/4 *Н.

11,313708*11,313708=­128,0000

128:4=32

32*3,14=100,48.

Далее умножим на Н

100,48*5,65685 = 568,4003

Найденый объем цилиндра 568,4003

Если объем тела V существует и функция S=S(x) является площадью сечения тела плоскостью (определенная и гладкая на промежутке [a;b]), каторая перпендикулярная к оси Ox в точке x, то объем тела находится за формулой
Это достаточно простая зависимость определенного интеграла, проблема заключается в том, что функция площади не всегда выражается простой зависимостью. В этом Вы скоро убедится из готовых ответов на вычисление объема.
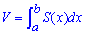
Примеры подобрано из программы для студентов мех-мата Львовского национального университета имени Ивана Франко. Студенты на практических занятиях имеют похожую программу учебы, задания в ряде случаев совпадают.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича). 

Для изучения методики нахождения объема тел за известными сечениями основные этапы интегрирования повторяться из примера в пример.

Найти объемы тел, которые ограничены следующими поверхностями

Пример 2463 Найти объем эллипсоида

Вычисление: Сложим уравнение подинтегральной функции. В сечении тела плоскостью, что перпендикулярная к оси Ox, получим эллипс

площадь которого выражается функцией

Определим пределы интегрирования:
у эллипсоида в канонической системе координат это промежуток [-a;a].
Найдем объем эллипсоида:

В том что формула справедлива можете убедиться, сопоставив вычисленную формулу с известной.
Объем фигур измеряется у кубических единиц !
Видим, если эллипсоид вырождается в сферу (a=b=c=R), то его объем равен V=4/3*Pi*R³ (формула известна из «школьной» геометрии).

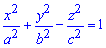
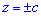
Пример 2464 Найти объем тела (однополий гиперболоид).
Вычисление: Выражаем подинтегральную функцию.
В сечении тела плоскостью, что перпендикулярная к оси Ox, получим эллипс

площадь которого выражается функцией

Определим пределы интегрирования : у эллипсоида в канонической системе координат это промежуток [- a;a].
Найдем объем эллипсоида :

В том что формула справедливая можете убедиться, сравнив вычисленную формулу с известными в справочниках.
Объем фигур измеряется у кубических единиц !
Видим, если эллипсоид вырождается в сферу (a=b=c=R), то его объем равен V=4/3*Pi*R³ (формула известна из «школьной» геометрии).

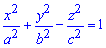
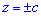
Пример 2464Найти объем тела (однополий гиперболоид).
Вычисление: Выражаемый подинтегральную функцию. В сечении тела плоскостью, что перпендикулярная к оси Oz, получим эллипс

площадь которого

Пределы интегрирования известны за условием: .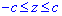
Кроме этого они являются подсказкой в каком направлении выполнять перерез и искать функцию площади.
Найдем объем однополого гиперболоида, что ограничен сверху и снизу плоскостями:

Определенный интеграл в этом задании находится без трудностей.

Пример 2465Найти объем тела образованного пересечением цилиндрических поверхностей
Вычисление: Сложим уравнение подинтегральной функции. Рассмотрим 1/8 часть тела (она расположена в И квадранте).
В сечении плоскостью, какая перпендикулярная к оси Oz, получим квадрат, площадь которого равна

Пределы интегрирования : И вадрат прямоугольной системы координат [0;a].
Интегрированием вычисляем объем тела :

Как можно убедиться из формул площади, их интегрирования достаточно не сложное.

Пример 2468Вычислить объем тела
Вычисление: Выражаемый подинтегральную функцию. В сечении плоскостью, какая перпендикулярная к оси Oz, получим эллипс, площадь которого известна
Пределы интегрирования за условием тоже известны:
.
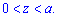
Осталось проинтегрировать и подставить пределы.

Получили, что объем тела равен V=Pi/2*a³ куб. од.

Пример 2469Найти объем тела
Вычисление: Запишем подинтегральную функцию. В сечении плоскостью, которая перпендикулярная к оси Oz, получим равнобедренный прямоугольный треугольник с катетом длиной 1-z², площадь которого легко находится

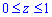
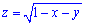
Пределы интегрирования : (это видно из области существования функции ).
Объем тела находим интегрированием:

Из приведенных примеров Вы могли заметить, что все зависит от уравнения площади сечения. Для того, чтобы его записать нужно владеть добрым пространственным воображением и знать сечения основных пространственных тел. Все остальное зависит от Вашего умения интегрировать.