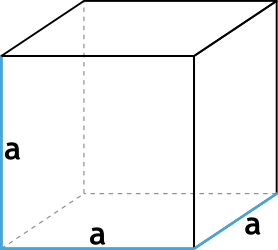
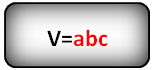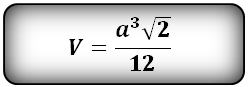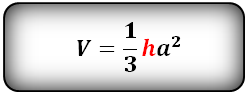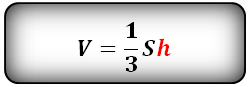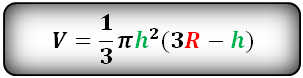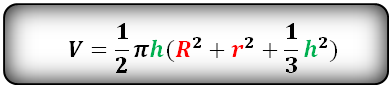Как найти объем куба через радиус

Рисунок куба, ребро

a — сторона куба

Формула объема куба, (V):

Формула объема куба

Изображение параллелепипеда

a, b, c — стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

Формула объема прямоугольного параллелепипеда

Рисунок шара, сферы

R — радиус шара

π ≈ 3.14

По формуле, если дан радиус, можно найти объема шара, (V):

Формула для расчета объема шара, сферы

Цилиндр радиус высота

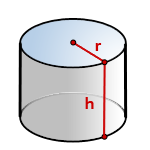
h — высота цилиндра

r — радиус основания

π ≈ 3.14

По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):

формула объема цилиндра

конус радиус основания высота

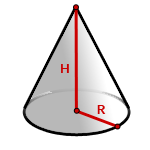
R — радиус основания

H — высота конуса

π ≈ 3.14

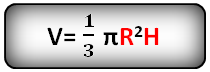
Формула объема конуса, если известны радиус и высота (V):

Формула объема конуса

усеченный конус, радиусы оснований и высота

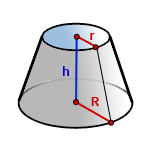
r —  радиус верхнего основания

R — радиус нижнего основания

h — высота конуса

π ≈ 3.14

Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса  (V ):

Формула объема усеченного конуса

тетраэдр

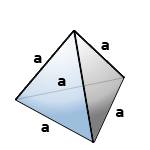
Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.

а — ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

Формула объема тетраэдра

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

правильная четырехугольная пирамида

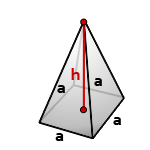
a — сторона основания

h — высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

формула объема правильной четырехугольной пирамиды

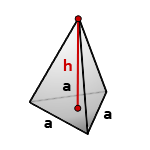
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

Правильная треугольная пирамида

a — сторона основания

h — высота пирамиды

Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):

Формула объема правильной треугольной пирамиды

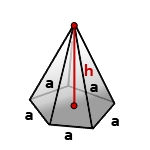
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

правильная пирамида

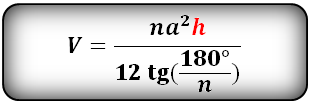
h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Объем правильной пирамиды

Расчет объема пирамиды

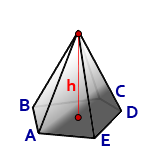
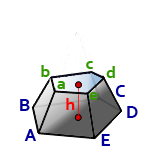
h — высота пирамиды

S — площадь основания ABCDE

Формула для вычисления объема пирамиды, если даны — высота и площадь основания (V):

Формула объема пирамиды

Расчёт объёма усечённой пирамиды

h — высота пирамиды

Sниж — площадь нижнего основания, ABCDE

Sверх — площадь верхнего основания, abcde

Формула объема усеченной пирамиды, (V):

Формула объема усеченной пирамиды

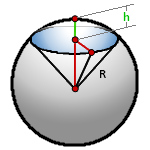
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

Объем шарового сегмента

R — радиус шара

h — высота сегмента

π ≈ 3.14

Формула для расчета объема шарового сегмента, (V):

Формула объема шарового сегмента

Объем шарового сектора

R — радиус шара

h — высота сегмента

π ≈ 3.14

Формула объема шарового сектора, (V):

Формула объема шарового сектора

Объем шарового слоя

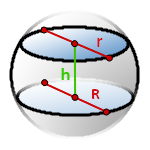
h — высота шарового слоя

R — радиус нижнего основания

r — радиус верхнего основания

π ≈ 3.14

Формула объема шарового слоя, (V):

Формула объема шарового слоя

Источник
Определение куба

Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.

объем куба

У куба 12 ребер – отрезков, которые являются сторонами квадратов (граней куба).
Также он имеет 8 вершин и 6 граней.

Онлайн-калькулятор объема куба

Формула объема куба

Для нахождения объема куба нужно перемножить его измерения – длину, ширину и высоту. Исходя из того, что куб состоит из квадратов, все его измерения одинаковы и численно равны длине ребра.

Формула для вычисления объема куба такова:

V=a3V=a^3

где aa — длина ребра куба.

Рассмотрим несколько примеров.

Задача 1

Найти объем куба, если периметр PP его грани aa равен 16 cм.16text{ cм.}

Решение

P=16P=16

Периметр PP грани куба связан с длиной его ребра aa по формуле:

P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a

16=4⋅a16=4cdot a

a=164=4a=frac{16}{4}=4

Найдем объем нашего тела:

V=a3=43=64 см3V=a^3=4^3=64text{ см}^3

Ответ: 64 см3.64text{ см}^3.

Задача 2

Одна четвертая часть диагонали квадрата равна 3 см.3text{ см.} Найти объем куба, образованного данным четырехугольником.

Решение

Пусть dd — диагональ фигуры, тогда по условию:

d4=3frac{d}{4}=3

d=4⋅3=12d=4cdot 3=12

Найдем сторону этого квадрата. Обратимся за помощью к теореме Пифагора:

a2+a2=12a^2+a^2=12,

где aa — сторона квадрата.

2⋅a2=122cdot a^2=12

a=6a=sqrt{6}

Приходим к окончательным расчетам для объема:

V=a3=(6)3=66 см3V=a^3=(sqrt{6})^3=6sqrt{6}text{ см}^3

Ответ: 66 см3.6sqrt{6}text{ см}^3.

Чуть более сложный пример.

Задача 3

В куб вписан шар, площадь SS которого равна 64π64pi. Найти объем куба.

Решение

S=64πS=64pi

Первый шагом является нахождение радиуса RR данного шара. Формула его площади такова:

S=4⋅π⋅R2S=4cdotpicdot R^2

64π=4⋅π⋅R264pi=4cdotpicdot R^2

64=4⋅R264=4cdot R^2

644=R2frac{64}{4}=R^2

16=R216=R^2

R=4R=4

Для куба радиус вписанного шара является половиной его стороны aa:

a=2⋅R=2⋅4=8a=2cdot R=2cdot4=8

Объем вычисляется следующим образом:

V=a3=83=512 см3V=a^3=8^3=512text{ см}^3

Ответ: 512 см3.512text{ см}^3.

На Студворке вы можете оформить заказ контрольных работ для студентов по самым низким ценам!

Тест по теме «Объем куба»

Источник

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

  • Определение куба

  • Свойства куба

    • Свойство 1

    • Свойство 2

    • Свойство 3

  • Формулы для куба

    • Диагональ

    • Диагональ грани

    • Площадь полной поверхности

    • Периметр ребер

    • Объем

    • Радиус описанного вокруг шара

    • Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Куб

  • Вершины куба – это точки, являющиеся вершинами его граней.
    Всего их 8: A, B, C, D, A1, B1, C1 и D1.
  • Ребра куба – это стороны его граней.
    Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1.
  • Грани куба – это квадраты, из которого состоит фигура.
    Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:

  • ABCD || A1B1C1D1
  • AA1B1B || CC1D1D
  • BB1C1C || AA1D1D

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

Пересечение диагоналей куба

  • AC1 = BD1 = A1C = B1D (диагонали куба).
  • О – точка пересечения диагоналей:
    AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Прямой двугранный угол куба

Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

  • a – ребро куба;
  • d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Формула для расчета диагонали куба через длину его ребра

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Формула для расчета диагонали грани куба через длину его ребра

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Формула расчета площади полной поверхности куба через длину его ребра/диагонали

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Формула расчета периметра куба через длину его ребра/диагонали

Объем

Объем куба равен длине его ребра, возведенной в куб.

Формула расчета объема куба через длину его ребра/диагонали

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Формула расчета радиуса шара описанного вокруг куба через длину его ребра/диагонали

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

Формула расчета радиуса вписанного в куб шара через длину его ребра/диагонали

Источник

Объем куба при заданном радиусе описанного цилиндра

Идти



Объем куба = (sqrt(2)*Описанный цилиндр Радиус куба)^(3)

Объем куба с учетом радиуса средней сферы

Идти



Объем куба = (sqrt(2)*Радиус средней сферы куба)^(3)

Объем куба с учетом пространственной диагонали

Идти



Объем куба = (Космическая диагональ куба/sqrt(3))^3

Объем куба при заданном радиусе окружности

Идти



Объем куба = (2/sqrt(3)*Окружность Радиус куба)^(3)

Объем куба по диагонали грани

Идти



Объем куба = (Диагональ грани куба/sqrt(2))^(3)

Объем куба при заданном отношении поверхности к объему

Идти



Объем куба = (6/Отношение поверхности к объему куба)^(3)

Объем куба с учетом площади боковой поверхности

Идти



Объем куба = (Площадь боковой поверхности куба/4)^(3/2)

Объем куба с учетом общей площади поверхности

Идти



Объем куба = (Общая площадь поверхности куба/6)^(3/2)

Объем куба при заданном радиусе вписанного цилиндра

Идти



Объем куба = (2*Вписанный цилиндр Радиус куба)^(3)

Объем куба с учетом периметра грани

Идти



Объем куба = (Лицевой периметр куба/4)^(3)

Объем куба с учетом радиуса Insphere

Идти



Объем куба = (2*Insphere Радиус куба)^(3)

Объем куба с учетом площади грани

Идти



Объем куба = Площадь грани куба^(3/2)

Объем куба по периметру

Идти



Объем куба = (Периметр куба/12)^(3)

Объем куба

Идти



Объем куба = Длина ребра куба^3

Объем куба с учетом пространственной диагонали

Идти



Объем куба = (Космическая диагональ куба/sqrt(3))^3

Объем куба при заданном радиусе окружности

Идти



Объем куба = (2/sqrt(3)*Окружность Радиус куба)^(3)

Объем куба с учетом общей площади поверхности

Идти



Объем куба = (Общая площадь поверхности куба/6)^(3/2)

Объем куба

Идти



Объем куба = Длина ребра куба^3

Источник

Куб — это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).

Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.

Содержание:
  1. калькулятор объема куба
  2. формула объема куба через ребро
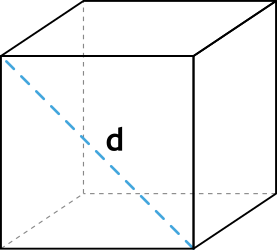
  3. формула объема куба через диагональ грани
  4. формула объема куба через периметр грани
  5. формула объема куба через диагональ куба
  6. формула объема куба через площадь полной поверхности
  7. примеры задач

Формула объёма куба через ребро

Объем куба через ребро

Формула объёма куба через диагональ грани

Объем куба через диагональ грани

{V = Big( dfrac{d}{sqrt{2}} Big) ^3}

d — диагональ грани куба

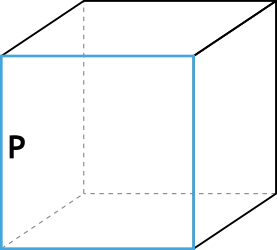
Формула объёма куба через периметр грани

Объем куба через периметр грани

{V= Big( dfrac{P}{4} Big) ^3}

P — периметр грани куба

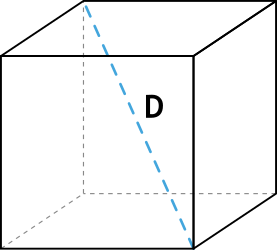
Формула объёма куба через диагональ куба

Объем куба через диагональ куба

{V= dfrac{D^3}{3sqrt{3}}}

D — диагональ куба

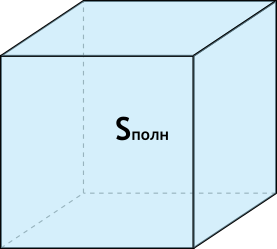
Формула объёма куба через площадь полной поверхности

Объем куба через площадь полной поверхности

{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}

Sполн — диагональ куба

Примеры задач на нахождение объема куба

Задача 1

Чему равен объём куба с ребром 5 см?

Решение

Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:

V=a ^ 3 = 5 ^ 3 = 125 : см^3

Ответ: 125 см³

Воспользуемся калькулятором для проверки полученного результата.

Задача 2

Найти объем куба, если площадь его поверхности равна 96 см².

Решение

В данном примере нам подойдет эта формула:

V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3

Ответ: 64 см³

Проверить ответ поможет калькулятор .

Также на нашем сайте вы можете найти объем конуса.

Источник

Понравилась статья? Поделить с друзьями:
  • Как составить медиапланирование
  • Как исправить ошибку провайдера
  • Работа в москве как найти форум
  • Как найти приходится родившихся
  • Как найти песню через шазам в инстаграме