Как найти объем куба зная объем призмы - Исправление недочетов и поиск решений вместе с Examum.ru

Поскольку плоскость параллельна третьему ребру (на рисунке это высота куба), то эта плоскость отсекает от куба треугольную призму — в основании которой прямоугольный треугольник.

Пусть а — длина ребра куба.

Тогда

1) Объем призмы V=S(основания)*высоту.

S(основания) = 0,5*0,5*а*0,5*а= (1/8)*а^2, т.к. высота и основание прямоугольного треугольника равны половине длины ребра куба.

V=(1/8)*а^2*a=(1/8)*а^3=3,5

Отсюда: а^3 = 3,5 * 8 = 28

Поскольку объем куба это и есть а^3, то объем куба равен 28.

Ответ: V=28.

Источник

Миникурс по геометрии. Куб, призма, цилиндр и конус

Как найти объем куба
Как найти объем призмы
Как найти объем пирамиды
Как найти объем куба, призмы и пирамиды — метод
Объем Куба
Объем призмы
Объем Пирамиды
Как найти объем Куба, Призмы и Пирамиды — Примеры
Найти объем куба
Найти объем призмы
Найти объем пирамиды

Поскольку куб, призма и пирамида являются тремя основными твердотельными объектами в геометрии, необходимо знать, как найти объем куба, призмы и пирамиды. В математике, физических науках и технике свойства этих объектов имеют большое значение. В большинстве случаев геометрические и физические свойства более сложного объекта всегда аппроксимируются с использованием свойств твердых объектов. Объем является одним из таких свойств.

Как найти объем куба

Куб представляет собой твердый объект с шестью квадратными гранями, которые встречаются под прямым углом. Он имеет 8 вершин и 12 ребер, а его ребра равны по длине. Объем куба — это фундаментальный (возможно, самый простой для определения объем) объем всех твердых объектов. Объем куба определяется как:

V _cube = a ³, где a — длина его ребер.

Как найти объем призмы

Призма — это многогранник; это твердый объект, состоящий из двух конгруэнтных (похожих по форме и равных по размеру) многоугольных граней с одинаковыми краями, соединенными прямоугольниками. Многоугольная грань известна как основание призмы, а две базы параллельны друг другу. Однако не обязательно, чтобы они были точно расположены над другим. Если они расположены точно друг над другом, то прямоугольные стороны и основание встречаются под прямым углом. Этот вид призмы известен как прямоугольная призма.

Если площадь основания (многоугольной грани) равна A, а перпендикулярная высота между основаниями равна h, то объем призмы определяется по формуле:

V _призма = Ах

Результат остается верным, является ли это прямой призмой или нет.

Как найти объем пирамиды

Пирамида также является многогранником с многоугольным основанием и точкой (называемой вершиной), соединенной треугольниками, идущими от краев. У пирамиды есть только одна вершина, но количество вершин зависит от полигонального основания.

Объем пирамиды с базовой площадью A и перпендикулярной высотой к вершине h определяется как:

V _{пирамида} = 1/3 Ач

Как найти объем куба, призмы и пирамиды — метод

Объем Куба

Куб — самый легкий твердый объект, чтобы найти объем.

Найти длину одной стороны (рассмотрим)
Увеличьте это значение до степени 3, т. Е. До ³ (найдите куб)
Результирующее значение — это объем куба.

Единицей объема является куб единицы измерения, в которой была измерена длина. Поэтому, если стороны были измерены в метрах, объем дается в кубических метрах.

Объем призмы

Найдите площадь любого основания призмы (A) и определите перпендикулярную высоту между двумя основаниями (h).
Произведение площади h на перпендикулярную высоту дает объем призмы.

Примечание. Этот результат действителен для любого типа призмы, обычной или нерегулярной.

Объем Пирамиды

Найдите площадь основания пирамиды (A) и определите перпендикулярную высоту от основания до вершины (h).
Возьмите произведение площади основания и перпендикулярной высоты. Одна треть полученных значений — это объем пирамиды.

Примечание. Этот результат действителен для любого типа призмы, обычной или нерегулярной.

Как найти объем Куба, Призмы и Пирамиды — Примеры

Найти объем куба

1. Край куба имеет длину 1, 5 метра. Найдите объем куба.

Длина куба составляет 1, 5 метра. Если не дано напрямую, найдите длину, используя другие геометрические средства или измерения.
Возьмите третью степень длины. То есть (1, 5) ³ = 1, 5 × 1, 5 × 1, 5 = 3, 375 м ³
Куб имеет объем 3, 375 куб.

Найти объем призмы

2. Треугольная призма имеет длину 20см. Основание призмы представляет собой равнобедренный треугольник с равными сторонами, образующий угол 60 ^° . Если длина стороны, противоположной углу, составляет 4 см, найдите объем пирамиды.

Сначала определим площадь основания. По тригонометрическим соотношениям мы можем определить перпендикулярную высоту базового треугольника от края 4 см до противоположной вершины как 2 tan 60 ⁰ = 2 × √3≅3, 4641 см. Следовательно, площадь основания составляет 1/2 × 4 × 3, 4641 = 6, 9298 см ^2.
Высота перпендикуляра (как длина) составляет 20см. Теперь мы можем рассчитать объем путем умножения площади основания на перпендикулярную высоту, например, V _призма = A × h = 6, 9298 см ² × 20 см = 138, 596 см ³ .
Объем пирамиды составляет 138, 596 см ³ .

Найти объем пирамиды

3. Прямоугольная правая пирамида имеет основание шириной 40 м и длиной 60 м. Если высота до вершины пирамиды от основания составляет 20 м, найдите объем, окруженный поверхностью пирамиды.

Площадь основания может быть просто определена, взяв произведение длин двух сторон. Следовательно, площадь основания составляет 40 м × 60 м = 2400 м ^2.
Высота перпендикуляра равна 20м. Следовательно, объем пирамиды равен V _{пирамиде} = 1/3 × 2400 м ² × 20 м = 16 000 м ³

Пирамиды и Призмы

Пирамиды против Призмы Большинство людей ошибочно полагают, что призма такая же, как пирамида. Однако, стоит знать, что эти два на самом деле разные. Давайте рассмотрим их различия с точки зрения геометрии. Пирамида в геометрии представляет собой многогранник, образованный соединением многоугольной базы и точки

Как найти площадь поверхности призмы

Чтобы найти площадь поверхности призмы с правильными многоугольниками в качестве оснований, можно использовать следующую формулу: Общая площадь = 2 [Площадь основания] + n [Площадь стороны]. Общая площадь треугольной призмы = 2 [1/2 ах] +3 [ал]

Как найти объем цилиндра

Чтобы найти объем цилиндра, нужно знать только высоту и радиус цилиндра. Затем используйте формулу для объема цилиндра V = (pi) * r ^ 2 * h

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Начинающим учащимся геометрии обычно приходится находить объем, площадь поверхности куба и прямоугольную призму. Чтобы выполнить задачу, студент должен запомнить и понять применение формул, которые применяются к этим трехмерным фигурам. Объем относится к количеству пространства внутри объекта, измеренному в кубических единицах, в то время как площадь поверхности измеряет общее количество в квадратных единицах шести граней каждого объекта. Также важно сформулировать свой ответ, используя правильные единицы измерения, так как если вы этого не сделаете, вопрос будет помечен частично или полностью неверно.

Прямоугольная призма

Думайте об этой форме как о пустой картонной коробке. Его три измерения могут быть обозначены как длина, ширина и глубина. Они могут быть взаимозаменяемыми в зависимости от ориентации коробки.

Вычислите объем прямоугольной призмы по следующей формуле: Объем = длина, умноженная на ширину, умноженная на глубину. Например, предположим, что у вас была прямоугольная призма с размерами 3 на 4 на 5 футов. Умножьте размеры вместе, чтобы получить 60 кубических футов.

Рассчитайте площадь поверхности коробки. Для этого вычислите площадь каждого лица. Фигура состоит из трех пар конгруэнтных граней. Используя предыдущий пример, умножьте 3 на 4, чтобы вычислить площадь поверхности одной грани. Это равно 12 квадратных футов. Умножьте эту цифру на два для будущего противостоящей стороны, чтобы теперь у вас было 24 квадратных фута. Умножьте 4 на 5, чтобы вычислить площадь поверхности другой стороны, получая 20 квадратных футов. Умножьте этот продукт на два, чтобы включить противоположную сторону. Таким образом, 20 х 2 = 40 квадратных футов. Затем умножьте 3 на 5, чтобы вычислить площадь поверхности конечной стороны, которая составляет 15 квадратных футов. Опять же, умножьте этот продукт на два, чтобы получить 30 квадратных футов. Сложите результаты: 24 + 40 + 30 = 94 квадратных фута.

Рассчитайте площадь поверхности, используя формулу, как только вы поймете концепцию. Формула для площади поверхности прямоугольной пирамиды: Area = 2lw + 2ld + 2wd, где «l» — длина, «w» — ширина, а «d» — глубина.

куб

Вычислить объем куба. Поскольку все стороны куба равны, формула объема V = s ^ 3, где «s» — длина одной стороны. Например, если бы куб имел ребро, охватывающее 4 дюйма, его объем был бы 4 ^ 3 или 64 кубических дюйма.

Найдите площадь поверхности куба. Поскольку каждая грань имеет площадь поверхности s ^ 2, а каждый куб имеет шесть граней, формула имеет следующий вид: Площадь поверхности = 6s ^ 2. Например, если куб имеет ребро 5 см, площадь поверхности будет 6 * 5 ^ 2 или 150.

Добавьте правильные единицы в ваш ответ. В примере вы бы написали: «150 квадратных см».

Источник

Факт 1.
(bullet) Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
(bullet) Следовательно:

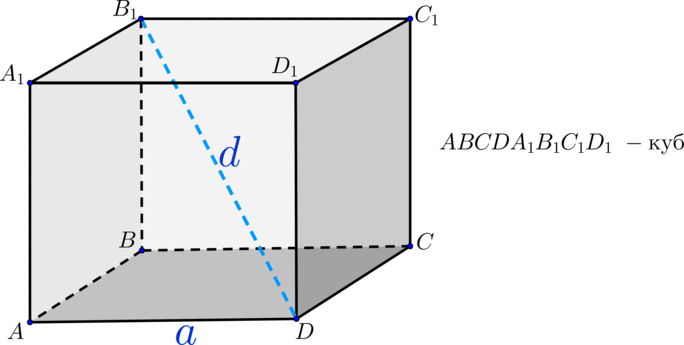
— ({color{red}{{small{объем куба}}}}) ищется по следующей формуле (где (a) – ребро куба): [{color{red}{{large{V=a^3}}}}] — ({color{red}{{small{диагональ куба}}}}) [{color{red}{{large{d^{,2}=3a^2}}}}] — ({color{red}{{small{площадь поверхности куба}}}}) равна сумме площадей шести одинаковых квадратов, т.е. [{color{red}{{large{S_{text{пов.куб}}=6a^2}}}}]

Факт 2.
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.

Источник

Миникурс по геометрии. Куб, призма, цилиндр и конус

Оглавление:

Как найти объем куба

Как найти объем призмы

Как найти объем пирамиды

Как найти объем куба, призмы и пирамиды — метод

Объем Куба

Объем призмы

Объем Пирамиды

Как найти объем Куба, Призмы и Пирамиды — Примеры

Найти объем куба

Найти объем призмы

Найти объем пирамиды

Пирамиды и Призмы

Как найти площадь поверхности призмы

Как найти объем цилиндра

Формулы объёма и площади поверхности. Многогранники.

Прямоугольная призма

куб