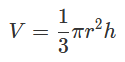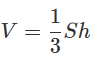Как найти объем квадратного конуса - Исправление недочетов и поиск решений вместе с Examum.ru

Калькулятор объема конуса

Рассчитайте онлайн объем для любых конусовидных объектов в кубических метрах или литрах.

Что известно

Размерность

Радиус основания

см

Диаметр основания

см

Площадь основания

см²

Высота

см

Раcсчитать

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

🧮 Что такое калькулятор объема конуса?

Калькулятор объема конуса — это онлайн инструмент, который позволяет вычислить объем конуса при заданных значениях его радиуса основания и высоты.

Данный онлайн-калькулятор удобен для быстрого и точного расчета объема конуса без необходимости вручную применять формулу для расчета.

Какую формулу использует калькулятор?

Калькулятор объема конуса онлайн использует формулу для расчета объема правильного конуса, которая выглядит следующим образом:

V = 1/3 * π * r² * h

где V — объем конуса, π — математическая константа (приблизительно равна 3,14159), r — радиус основания конуса, h — высота конуса.

В чем может быть полезен такой калькулятор?

Калькулятор объема конуса онлайн может быть полезен в различных областях, например:

В учебной деятельности — калькулятор позволяет быстро и удобно вычислять объем конуса при решении задач в школе, вузе или других образовательных учреждениях.
В профессиональной деятельности — инженеры, архитекторы, дизайнеры и другие специалисты могут использовать калькулятор для расчета объемов конических форм в проектах, таких как проектирование зданий, оборудования и т.д.
В повседневной жизни — калькулятор может пригодиться при решении бытовых задач, например, при расчете объема цветочного горшка в форме конуса, объема мороженого в стаканчике или других предметов, имеющих форму конуса.
В производстве — калькулятор может использоваться для расчета объема конических контейнеров, таких как силосы, резервуары, баки и т.д. Это может помочь определить необходимый объем материала, который нужно использовать при изготовлении таких контейнеров, и при планировании их транспортировки и хранения.

Также калькулятор объема конуса онлайн может быть полезен для тех, кто интересуется математикой и хочет изучить формулы и свойства конуса более подробно.

Какие преимущества имеет коническая форма?

Конусообразная форма имеет ряд преимуществ в различных областях:

Прочность — из-за своей конической формы конструкции, такие как башни, мачты и башенные краны, имеют высокую прочность и устойчивость к ветру и другим нагрузкам.
Эффективность — конические формы могут быть эффективными для передачи или направления потока жидкости, газа или другого материала, так как конусное сужение может ускорять поток, повышая его скорость.
Удобство — конические формы могут быть удобными для хранения и транспортировки предметов, так как они занимают меньше места при хранении, чем другие формы.
Эстетика — конические формы могут иметь эстетическую привлекательность и использоваться в дизайне зданий, мебели, украшений и т.д.
Возможность распределения нагрузок — коническая форма может распределять нагрузки на более широкую область, что позволяет уменьшить напряжения и повысить прочность конструкций.
Простота конструкции — конические формы могут быть проще в изготовлении и сборке, так как они имеют меньшее количество деталей и сложных соединений, чем другие формы.

❓Вопросы и ответы

Часто задаваемые вопросы и ответы по калькулятору объема конуса онлайн.

Что такое калькулятор объема конуса онлайн?

Калькулятор объема конуса онлайн — это инструмент, который позволяет рассчитать объем конуса на основе его радиуса и высоты.

Как использовать калькулятор объема конуса онлайн?

Для использования калькулятора нужно ввести значение радиуса и высоты конуса в соответствующие поля и нажать кнопку «Рассчитать». Результат, т.е. объем конуса, будет показан ниже.

Можно ли использовать калькулятор для расчета объема усеченного конуса?

Нет, калькулятор объема конуса онлайн не предназначен для расчета объема усеченного конуса.

Можно ли использовать калькулятор объема конуса для расчета объема других трехмерных фигур?

Нет, калькулятор объема конуса онлайн предназначен только для расчета объема конуса. Для расчета объема других трехмерных фигур существуют другие калькуляторы.

Могу ли я использовать дробные значения для радиуса и высоты конуса?

Да, вы можете использовать дробные значения для радиуса и высоты конуса в калькуляторе объема конуса онлайн.

Для каких целей может быть полезен калькулятор объема конуса онлайн?

Калькулятор объема конуса онлайн может быть полезен для профессионалов, работающих в области строительства, дизайна и инженерии, а также для учеников и студентов, изучающих геометрию и математику.

Я не знаю, как найти радиус и высоту конуса. Что мне делать?

Радиус и высота конуса могут быть определены с помощью соответствующих измерений или данных. Если у вас нет этих данных, вы можете попробовать использовать другие методы расчета объема конуса, такие как измерение площади основания и умножение на высоту, но для этого вам нужно знать другие параметры конуса.

Как рассчитать объем конуса

На данной странице калькулятор поможет рассчитать объем конуса онлайн. Для расчета задайте высоту, радиус или площадь. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

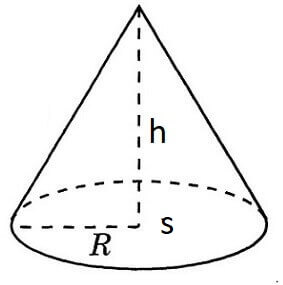
Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

Через высоту и радиус

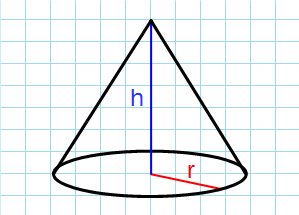
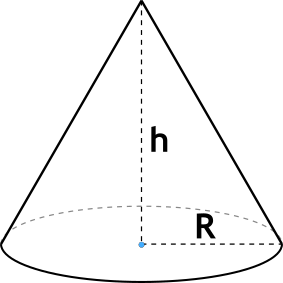
Формула объема конуса через радиус и высоту:

π — константа равная (3.14); h — высота конуса; r — радиус основания конуса.

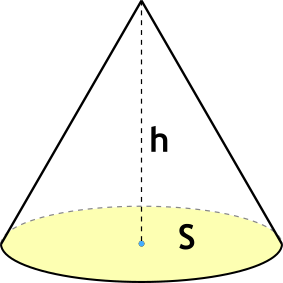
Через высоту и площадь основания

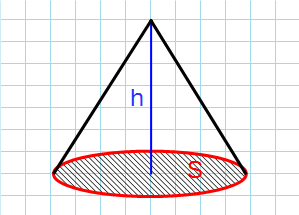
Формула объема конуса через высоту и площадь основания:

h — высота конуса; S — площадь основания.

Источник

{V=dfrac {1}{3} pi r^2 h}

Конус — это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра — высоту (h) и радиус основания (r).

Содержание:

калькулятор объема конуса
формула объема конуса через высоту и радиус
формула объема конуса через площадь основания и высоту
формула объёма усеченного конуса
примеры задач

Если мы сравним формулу объема конуса с формулой объема цилиндра, то мы увидим, что объем конуса в 3 раза меньше объема цилиндра с той же высотой и радиусом основания.

Наш калькулятор может рассчитать объем конуса через радиус основания и высоту, площадь основания и высоту, а также объем усеченного конуса через его высоту и радиусы нижнего и верхнего оснований.

Кроме того объем конуса можено найти, подставив значения в формулы, приведенные ниже.

Формула объёма конуса через радиус и высоту

{V=frac {1}{3} pi r^2 h}

r — радиус основания конуса,

h — высота конуса

Формула объёма конуса через площадь основания и высоту

{V=frac {1}{3} S h}

S — площадь основания конуса,

h — высота конуса

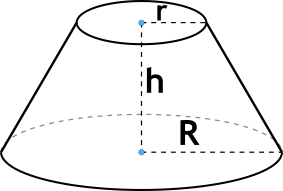
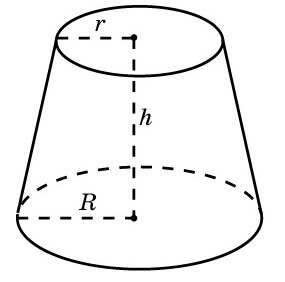
Формула объёма усеченного конуса

{V=frac {1}{3} pi h(r^2 + r R + R^2)}

h — высота усеченного конуса,

r — радиус меньшего основания усеченного конуса,

R — радиус большего основания усеченного конуса.

Примеры задач на нахождение объема конуса

Задача 1

Найдем объем конуса, высота которого 30см, а радиус основания 20см.

Решение

Подставим эти значения в формулу и произведем расчет:

V=dfrac {1}{3} pi r^2 h = dfrac {1}{3} cdot pi cdot 20^2 cdot 30 = dfrac {1}{3} cdot pi cdot 12000 = 400 pi : см^3 approx 12 566,37 : см^3

Ответ: {400 pi : см^3 approx 12 566,37 : см^3}

Проверить результат можно с помощью калькулятора .

Задача 2

Найдем объем конуса с высотой 3 см и диаметром основания 8 см².

Решение

Подставим эти значения в формулу и произведем расчет:

V=dfrac {1}{3} S h = dfrac {1}{3} cdot 8 cdot 3 = dfrac {1}{3} cdot 24 = 8 : см^3

Ответ: 8 см³

Воспользуемся калькулятором для проверки результата.

Задача 3

Найдите объем усеченного конуса радиусы оснований которого равны 1 см и 2 см, а высота равна 3 см.

Решение

Подставим высоту и радиусы оснований в формулу и произведем расчет:

V=dfrac {1}{3} pi h(r^2 + r R + R^2) = dfrac {1}{3} pi cdot 3 cdot (1^2 + 1 cdot 2 + 2^2) = dfrac {1}{3} pi cdot 3 cdot (1 + 2 + 4) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = 7 pi : см^3 approx 21,99115 : см^3

Ответ: {7 pi : см^3 approx 21,99115 : см^3}

Проверим полученный ответ.

Источник

Volume of a cone can be described as the space occupied by the cone or it is the capacity of the cone. Cone is a 3-D object having a circular flat base and a pointed top called an apex or vertex.

A cone is a solid three-dimensional geometric object with a circular base and a sharp edge at the top known as the apex. It is a form with a curving top and a round base. A cone has one face, one vertex, and no edges. Its slant height is the length of the line segment from the peak of the cone to any point on the circle of the cone’s base.

Volume of the Cone is the total space occupied by the cone in 3-D space. Let’s learn more about the volume of the cone its derivation and others in this article.

What is the Volume of a Cone?

A cone’s volume is defined as the amount of space or capacity it fills. The volume of a cone is measured in cubic units such as cm³, m³, in³, and so on. By rotating a triangle around any of its vertices, a cone can be produced. Volume of a cone can also be measured in litres.

Volume of a Cone Formula

A cone is a solid three-dimensional form having a circular base. It’s got a curved surface. The perpendicular height is the distance from the base to the vertex. A cone may be divided into two types: right circular cones and oblique cones. The vertex of the right circular cone is vertically above the centre of the base, but the vertex of the oblique cone is not vertically above the centre of the base.

The formula for the volume of a cone is given:

V = $frac{1}{3}pi r^2h$

where,
r is the radius of the cone,
h is the height of the cone,
π is constant with value 22/7 or 3.14

Also, the relationship between the cone’s volume and slant height by applying Pythagoras’ theorem to it is given by,

h² + r² = L²

h = √(L² – r²)

Hence, the volume of cone in terms of its slant height is given by,

V = $frac{1}{3}pi r^2(sqrt{L^2-r^2})$

where,
r is the radius of the cone,
L is the slant height of the cone,
π is constant with value 22/7 or 3.14

Click here for, Surface area of a Cone

Volume of a Cone Derivation

Suppose we have a cone with a circular base whose radius is r and height is h.

We know that the volume of a cone is equal to one-third of the volume of a cylinder having the same base radius and height.

So, the volume becomes,

V = 1/3 x Circular Base area x Height

= 1/3 x πr² x h

= πr²h/3

This derives the formula for the volume of a cone.

How to Find the Volume of a Cone?

Let’s consider an example to determine the volume of a cone.

Example: Determine the volume of a cone if the radius of its circular base is 3 cm and the height is 5 cm.

Step 1: Note the radius of the circular base (r) and the height of the cone (h).

Here, the radius is 3 cm and the height is 5 cm.

Step 2: Calculate the area of the circular base = πr². Substitute the value of r and π in the given equation,

i.e., 3.14 × (3)² = 28.26 cm².

Step 3: We know that the volume of a cone is (1/3) × (area of the circular base) × height of the cone.

Then, substitute the values in the equation = (1/3) × 28.26 × 5 = 47.1 cm³.

Step 4: Hence, the volume of the given cone is 47.1 cm³.

Using the steps discussed above the volume of a cone can be calculated.

Volume of Frustum of Cone

The frustum is the sliced part of a cone, and the volume of the frustum of the cone is the amount of liquid any frustum can hold. So for calculating the volume, we need to find the difference in the volumes of the two cones.

Know more on Frustum of Cone

Volume of Frustum of Cone Formula

The formula for finding the volume of the frustum of a cone is given by subtracting the volume of two cones.

Study the given figure for finding the volume of the frustum.

From the above figure, we have,

The total height H’ = H+h

The total slant height L = l₁ +l₂

The radius of the cone = r and the radius of the sliced cone = r’

Now the volume of the bigger cone = 1/3 π r² H’ = 1/3 π r² (H+h)

Volume of the smaller cone = 1/3 π(r’)²h. The volume of the frustum can be calculated by the difference between the two cones, i.e.

Volume of Frustum = 1/3 π r² H’ -1/3 π(r’)²h
= 1/3π r² (H+h) – 1/3 π(r’)²h
= 1/3 π [ r² (H+h) – (r’)² h ] ………(1)

Using the properties of similar triangles in Δ QPS and Δ QAB. we have,

r/ r’ = H+h / h

H+h = (rh)/r’

Substituting the value of H+h in the formula for the volume of frustum we get,

Volume of frustum = 1/3 π [r² (rh/r’) – (r’)² h]
= 1/3 π [r³h/r’ – (r’)² h]
= 1/3 π h (r³/r – (r’)²)
= 1/3 π h [{r³– (r’)³} / r]

Volume of Frustum of Cone = 1/3 π h [{r³ – (r’)³} / r]

where,
r is the radius of the lower base of the frustum of cone,
r’ is the radius of the upper base of the frustum of cone,
h is the height of the smaller cone,
π is constant with value 22/7 or 3.14

Volume of Cone with Height and Radius

The volume of the cone if its height(h) and radius(r) are given is calculated using the formula,

V = (1/3)πr²h cubic units

Volume of Cone with Height and Diameter

As we know,

r = d/2

where,
r is the radius of the base of the cone
d is the diameter of the base of the cone

The volume of the cone if its height(h) and diameter(d) are given is calculated using the formula,

V = (1/12)πd²h cubic units

Volume of Cone with Slant Height

For a cone with height ‘h’ and radius ‘r’ the slant height ‘L’ of the cone is given by the formula,

h² + r² = L²

h = √(L² – r²)

Then the volume of the cone in terms of slant height is,

V = (1/3)πr²h

V = (1/3)πr²√(L² – r²)

where,
r is the radius of the cone
L is the Slant Height

Volume of a cone (If Radius and Height are doubled)

Suppose,

Radius of the cone (r) = 2r

Height of the Cone (h) = 2h

Then the volume of a cone is given as,

Volume of a cone = (1/3)π(2r)²(2h) cubic units

V = (⅓)π(4r²)(2h)

V = (8/3)πr²h

Thus, volume of a cone becomes 8 times the original volume i.e. V = (8/3)πr²h, when its radius and height are doubled.

Volume of a cone (If Radius and Height are Halved)

Suppose,

Radius of the cone (r) = r/2

Height of the Cone (h) = h/2

Then the volume of a cone is given as,

Volume of a cone = (1/3)π(r/2)²(h/2) cubic units

V = (⅓)π(r²/4)(h/2)

V = (1/24)πr²h

Thus, volume of a cone becomes 1/8 times the original volume i.e. V = (1/24)πr²h, when its radius and height are halved.

Related Resources

Surface Area of a Cone

Volume of Sphere

Solved Example on Volume of a Cone

Example 1. Find the volume of a cone for a radius of 7 cm and height of 14 cm.

Solution:

We have, r = 7 and h = 14.

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (7) (7) (14)

= (1/3) (7) (7) (2)

= 32.66 cm³

Example 2. Find the volume of a cone for a radius of 5 cm and height of 9 cm.

Solution:

We have, r = 5 and h = 9.

Volume of cone = 1/3 πr²h

= (1/3) (3.14) (5) (5) (9)

= (3.14) (5) (5) (3)

= 235.49 cm³

Example 3. Find the volume of a cone for a radius of 7 cm and height of 12 cm.

Solution:

We have, r = 7 and h = 12.

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (7) (7) (12)

= (22) (7) (4)

= 616 cm³

Example 4. Find the volume of a cone for a radius of 8 cm and height of 15 cm.

Solution:

We have, r = 8 and h = 15.

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (8) (8) (15)

= (1/3) (22/7) (8) (8) (5)

= 335.02 cm³

Example 5. Find the volume of a cone for a diameter of 24 cm and a slant height of 13 cm.

Solution:

We have, 2r = 24

r = 24/2

r = 12

Also, l = 13.

Volume of cone = 1/3 πr² √(l² – r²)

= (1/3) (22/7) (12) (12) (√(13² – 12²)

= (1/3) (22/7) (12) (12) (5)

= 754.28 cm³

Example 6. Find the volume of a cone for a diameter of 16 cm and a slant height of 10 cm.

Solution:

We have, 2r = 16

r = 16/2

r = 8

Also, l = 10.

Volume of cone = 1/3 πr² √(l² – r²)

= (1/3) (22/7) (8) (8) (√(10² – 8²)

= (1/3) (22/7) (8) (8) (6)

= 402.048 cm³

Example 7. Find the volume of a cone for the height of 8 cm and the slant height of 17 cm.

Solution:

We have h = 8 and l = 10.

Find the value of r.

r = √(l² – h²)

= √(17² – 8²)

= √(289 – 64)

= 15

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (15) (15) (8)

= (1/3) (22/7) (5) (15) (8)

= 1884.6 cm³

FAQs on Volume of a Cone

Q1: What is volume of a cone?

Answer:

Volume of a cone is defined as the total capacity of the liquid a cone can hold in 3-dimension. It is the total space occupied by the cone.

Q2: Why cone volume is 1/3 of a cylinder?

Answer:

Experimentally it is clear that a cylinder can hold three times the volume of liquid as compared to a cone of similar dimensions. Thus, the volume of a cone is 1/3 of a cylinder

Q3: How to find volume of a cone with slant height?

Answer:

The volume of the cone if its slant height is given is calculated using the formula,

V = (1/3)πr²√(L² – r²)

where,
r is the radius of the cone
L is the Slant Height

Q4: What is the formula for the total surface area of a cone?

Answer:

Total surface area of a cone is given by the formula

TSA of Cone = πr(l + r) square units

where,
r is the radius of the circular base
l is the slant height of the cone

Q5: What is the formula for the volume of a cone?

Answer:

Volume of a cone is given by the formula

Volume of Cone = ⅓ πr² h cubic units

where,
r is the radius of the circular base
h is the height of the cone

Q6: What is the relation between the Volume of the cylinder and the volume of a cone with similar dimensions?

Answer:

Volume of a cylinder = πr²h

Volume of a cone = 1/3πr²h

Thus from the above formulas it is clear that one-third of the volume of a cylinder is equal to the volume of a cone, having the same radius and height.

Q7: What is the formula for the slant height of a cone?

Answer:

The slant height(l) of a cone is calculated using the formula,

l = √(h² + r²)

where,
h is the height of the cone
r is the radius of the circular base

Q8: How to find the volume of a cone, if the height and diameter of the cone are given?

Answer:

We know that,

Volume of a Cone = (1/3)πr²h cubic units

where
r is radius and h is height

Since,
(radius)r = (diameter)d/2

The volume of a cone becomes

V = (1/3)π(d/2)²h cubic units

V = (1/12)πd²h cubic units

Hence, this formula for the volume of a cone if its height(h) and diameter(d) are given.

Источник

Калькулятор объёма конуса

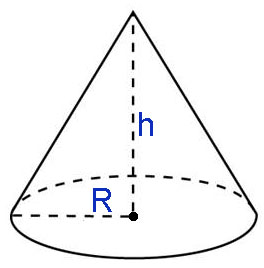
Расчёт объёма конуса

Вид конуса:

Неверный ввод

Введите размеры в мм:

Считаем через:

Высоту и радиус

Высоту и площадь

Неверный ввод

Радиус усеч , r

Неверный ввод

Радиус для усеч, R

Неверный ввод

Высота, ус h

Неверный ввод

Радиус для промого, R

Неверный ввод

Площадь, прям s

Неверный ввод

Высота, прям h

Неверный ввод

Выводим результат в:

Неверный ввод

Решение по формуле:

Формула объема конуса через радиус и высоту:

π — константа равная (3.14); h — высота конуса; r — радиус основания конуса.

Формула объема конуса через высоту и площадь основания:

h — высота конуса; S — площадь основания

Формула объема усеченного конуса через радиусы и высоту:

π — константа равная (3.14); r1 — радиус верхнего основания ; r2 — радиус нижнего основания; h — высота усеченного конуса.

Скачать, сохранить результат

Выберите способ сохранения

Вы можете сохранить результат расчёта в формате PDF на ваше устройство.
Распечатайте результат расчёта конструкции на бумагу любого формата.
Отправьте результат расчета в формате PDF на ваш е-мейл.

Информация

Математика является основой всего, что нас окружает. Она особенно важна в таких сферах деятельности, как технологии, строительство и техника. Еще в средней школе дети начинают изучать различные математические законы, формулы и много другое. Одной из важнейших формул выступает формула, по которой находится объем конуса. Данная формула применяется специалистами во многих видах деятельности. Также часто применяется формула, по которой вычисляют объем усеченного конуса.

В профессиональной деятельности у инженера или строителя нет права на допущение ошибки. Это связанно с тем, что их ошибка может стоить кому-нибудь жизни. Для того, чтобы облегчить и обезопасить расчеты в профессиональной деятельности, был создан такой инструмент, как онлайн-калькулятор. Он позволяет совершать вычислительные действия любых показателей, вводя исходные значения в формулу. Калькулятор выдает предельно точный результат и исключает возможность возникновения ошибки в процессе вычислений.

Для вычислений в данном калькуляторе используется три основные формулы:

Формула для вычисления объема конуса через радиус и высоту.
Формула отвечающая на вопрос « Как найти объем конуса через площадь его основания и высоту?».
Последняя формула позволяет найти объем усеченного конуса, зная радиус и высоту.

Используя наш онлайн-калькулятор, Вы получаете следующие выгоды:

Точность и достоверность результатов проведенного вычисления, которая полностью исключает ошибки в процессе осуществления профессиональной деятельности.
Экономия времени, благодаря исключению необходимости самостоятельных расчетов.
Интерфейс нашего калькулятора разработан максимально простым и удобным.

Для того, чтобы использовать наш онлайн-калькулятор, необходимо совершить следующие действия:

Выбрать вид конуса (прямой или усеченный).
Ввести исходные данные (высота, радиус, площадь).
Введя необходимы данные калькулятор автоматически сообщит, что объем конуса равен тому или иному значению.

Добавить комментарий

Источник

Калькулятор объема конуса

🧮 Что такое калькулятор объема конуса?

Какую формулу использует калькулятор?

В чем может быть полезен такой калькулятор?

Какие преимущества имеет коническая форма?

❓Вопросы и ответы

Что такое калькулятор объема конуса онлайн?

Как использовать калькулятор объема конуса онлайн?

Можно ли использовать калькулятор для расчета объема усеченного конуса?

Можно ли использовать калькулятор объема конуса для расчета объема других трехмерных фигур?

Могу ли я использовать дробные значения для радиуса и высоты конуса?

Для каких целей может быть полезен калькулятор объема конуса онлайн?

Я не знаю, как найти радиус и высоту конуса. Что мне делать?

Похожие калькуляторы

Есть что добавить?

Как рассчитать объем конуса

Через высоту и радиус

Через высоту и площадь основания

Содержание:

Формула объёма конуса через радиус и высоту

Формула объёма конуса через площадь основания и высоту

Формула объёма усеченного конуса

Примеры задач на нахождение объема конуса

What is the Volume of a Cone?

Volume of a Cone Formula

Volume of a Cone Derivation

How to Find the Volume of a Cone?

Volume of Frustum of Cone

Volume of Frustum of Cone Formula

Volume of Cone with Height and Radius

Volume of Cone with Height and Diameter

Volume of Cone with Slant Height

Volume of a cone (If Radius and Height are doubled)

Volume of a cone (If Radius and Height are Halved)

Solved Example on Volume of a Cone

FAQs on Volume of a Cone

Q1: What is volume of a cone?

Q2: Why cone volume is 1/3 of a cylinder?

Q3: How to find volume of a cone with slant height?

Q4: What is the formula for the total surface area of a cone?

Q5: What is the formula for the volume of a cone?

Q6: What is the relation between the Volume of the cylinder and the volume of a cone with similar dimensions?

Q7: What is the formula for the slant height of a cone?

Q8: How to find the volume of a cone, if the height and diameter of the cone are given?

Калькулятор объёма конуса

Калькулятор объёма конуса

Расчёт объёма конуса

Решение по формуле:

Скачать, сохранить результат

Выберите способ сохранения

Информация

Для вычислений в данном калькуляторе используется три основные формулы:

Добавить комментарий